Consider an infinite dimensional diffusion process process on TZd, where T is the circle, defined by the action of its generator L on C2(TZd) local functions as $Lf(\eta)=\sum_{i\in{\bf Z}^d}\left(\frac{1}{2}a_i \frac{\partial^2 f}{\partial \eta_i^2}+b_i\frac{\partial f}{\partial \eta_i}\right)$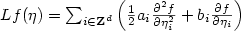. Assume that the coefficients, ai and bi are smooth, bounded, finite range with uniformly bounded second order partial derivatives, that ai is only a function of $\eta_i$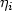 and that $\inf_{i,\eta}a_i(\eta)>0$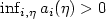. Suppose ν is an invariant product measure. Then, if ν is the Lebesgue measure or if d=1,2, it is the unique invariant measure. Furthermore, if ν is translation invariant, then it is the unique invariant, translation invariant measure. Now, consider an infinite particle spin system, with state space {0,1}Zd, defined by the action of its generator on local functions f by $Lf(\eta)=\sum_{x\in{\bf Z}^d}c(x,\eta)(f(\eta^x)-f(\eta))$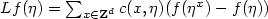, where $\eta^x$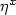 is the configuration obtained from η altering only the coordinate at site x. Assume that $c(x,\eta)$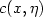 are of finite range, bounded and that $\inf_{x,\eta}c(x,\eta)>0$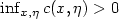. Then, if ν is an invariant product measure for this process, ν is unique when d=1,2. Furthermore, if ν is translation invariant, it is the unique invariant, translation invariant measure. The proofs of these results show how elementary methods can give interesting information for general processes.