Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gantert, Nina
van der Hofstad, Remco
and
König, Wolfgang
2006.
Deviations of a random walk in a random scenery with stretched exponential tails.
Stochastic Processes and their Applications,
Vol. 116,
Issue. 3,
p.
480.
Ermakov, Mikhail
2007.
Importance sampling for simulations of moderate deviation probabilities of statistics.
Statistics & Decisions,
Vol. 25,
Issue. 4/2007,
Eichelsbacher, Peter
and
König, Wolfgang
2008.
Ordered Random Walks.
Electronic Journal of Probability,
Vol. 13,
Issue. none,
Löwe, Matthias
and
Vermet, Franck
2009.
Capacity bounds for the CDMA system and a neural network: a moderate deviations approach.
ESAIM: Probability and Statistics,
Vol. 13,
Issue. ,
p.
343.
Löwe, Matthias
and
Meiners, Raphael
2012.
Moderate Deviations for Random Field Curie-Weiss Models.
Journal of Statistical Physics,
Vol. 149,
Issue. 4,
p.
701.
Döring, Hanna
and
Eichelsbacher, Peter
2013.
Moderate Deviations via Cumulants.
Journal of Theoretical Probability,
Vol. 26,
Issue. 2,
p.
360.
Meiners, Raphael
and
Reichenbachs, Anselm
2013.
On the accuracy of the normal approximation for the free energy in the Random Energy Model.
Electronic Communications in Probability,
Vol. 18,
Issue. none,
Tsirelson, Boris
2014.
Moderate deviations on different scales: no relations.
Israel Journal of Mathematics,
Vol. 203,
Issue. 1,
p.
161.
Miao, Yu
and
Wang, Yanling
2014.
Moderate deviation principle for maximum-likelihood estimator.
Statistics,
Vol. 48,
Issue. 4,
p.
766.
Miao, Yu
Zhu, Jianan
and
Mu, Jianyong
2018.
Moderate deviation principle for m-dependent random variables*.
Lithuanian Mathematical Journal,
Vol. 58,
Issue. 1,
p.
54.
Bahier, Valentin
2019.
Characteristic polynomials of modified permutation matrices at microscopic scale.
Stochastic Processes and their Applications,
Vol. 129,
Issue. 11,
p.
4335.
Eichelsbacher, Peter
and
Löwe, Matthias
2019.
Lindeberg’s Method for Moderate Deviations and Random Summation.
Journal of Theoretical Probability,
Vol. 32,
Issue. 2,
p.
872.
Mijatović, Aleksandar
and
Vogrinc, Jure
2019.
Asymptotic variance for random walk Metropolis chains in high dimensions: logarithmic growth via the Poisson equation.
Advances in Applied Probability,
Vol. 51,
Issue. 4,
p.
994.
Gulisashvili, Archil
2019.
Gaussian Stochastic Volatility Models: Scaling Regimes, Large Deviations, and Moment Explosions.
SSRN Electronic Journal,
Deijfen, Maria
Hirscher, Timo
and
Lopes, Fabio
2019.
Competing frogs on ${\mathbb Z}^{d}$.
Electronic Journal of Probability,
Vol. 24,
Issue. none,
Gulisashvili, Archil
2020.
Gaussian stochastic volatility models: Scaling regimes, large deviations, and moment explosions.
Stochastic Processes and their Applications,
Vol. 130,
Issue. 6,
p.
3648.
Mohan, Manil T.
2021.
A central limit theorem and moderate deviation principle for the stochastic 2D Oldroyd model of order one.
Stochastics and Partial Differential Equations: Analysis and Computations,
Vol. 9,
Issue. 2,
p.
510.
Mohan, Manil T.
2021.
Moderate deviation principle for the 2D stochastic convective Brinkman–Forchheimer equations.
Stochastics,
Vol. 93,
Issue. 7,
p.
1052.
Panigrahi, Snigdha
Taylor, Jonathan
and
Weinstein, Asaf
2021.
Integrative methods for post-selection inference under convex constraints.
The Annals of Statistics,
Vol. 49,
Issue. 5,
Brosset, Fabien
Klein, Thierry
Lagnoux, Agnès
and
Petit, Pierre
2022.
Séminaire de Probabilités LI.
Vol. 2301,
Issue. ,
p.
239.
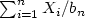 –
where $\frac {b_n} n \downarrow 0$
–
where $\frac {b_n} n \downarrow 0$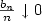 ,
but $\frac {b_n} {\sqrt n} \uparrow \infty$
,
but $\frac {b_n} {\sqrt n} \uparrow \infty$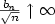 – to satisfy a moderate deviations
principle. Moreover we show that this equivalence is a typical moderate
deviations phenomenon. It is not true in a large deviations regime.
– to satisfy a moderate deviations
principle. Moreover we show that this equivalence is a typical moderate
deviations phenomenon. It is not true in a large deviations regime.


