Article contents
Coarse quantization for random interleaved sampling of bandlimited signals∗∗∗
Published online by Cambridge University Press: 11 January 2012
Abstract
The compatibility of unsynchronized interleaved uniform sampling with Sigma-Delta
analog-to-digital conversion is investigated. Let f be a bandlimited
signal that is sampled on a collection of N interleaved grids
{kT + Tn} k ∈ Z
with offsets \hbox{$\{T_n\}_{n=1}^N\subset [0,T]$}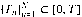 {Tn}n=1N⊂[0,T]. If the offsets Tn are
chosen independently and uniformly at random from [0,T] and if the
sample values of f are quantized with a first order Sigma-Delta
algorithm, then with high probability the quantization error \hbox{$|f(t) - \widetilde{f}(t)|$}
{Tn}n=1N⊂[0,T]. If the offsets Tn are
chosen independently and uniformly at random from [0,T] and if the
sample values of f are quantized with a first order Sigma-Delta
algorithm, then with high probability the quantization error \hbox{$|f(t) - \widetilde{f}(t)|$}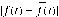 |f(t)−f(t)|is at most of order
N-1log N.
|f(t)−f(t)|is at most of order
N-1log N.
Keywords
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 46 , Issue 3: Special volume in honor of Professor David Gottlieb , May 2012 , pp. 605 - 618
- Copyright
- © EDP Sciences, SMAI, 2012
References
- 4
- Cited by


