Article contents
On the existence of variations, possibly with pointwise gradient constraints
Published online by Cambridge University Press: 12 May 2007
Abstract
We propose a necessary and sufficient condition about the existence of variations, i.e.,
of non trivial solutions $\eta\in W^{1,\infty}_0(\Omega)$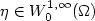 to the differential inclusion
$\nabla\eta(x)\in-\nabla u(x)+{\bf D}$
to the differential inclusion
$\nabla\eta(x)\in-\nabla u(x)+{\bf D}$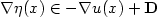 .
.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 2 , April 2007 , pp. 331 - 342
- Copyright
- © EDP Sciences, SMAI, 2007
References
- 1
- Cited by


