Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rossi, Riccarda
2006.
Free Boundary Problems.
Vol. 154,
Issue. ,
p.
369.
Ambrosio, Luigi
and
Savaré, Giuseppe
2007.
Vol. 3,
Issue. ,
p.
1.
Rossi, Riccarda
Segatti, Antonio
and
Stefanelli, Ulisse
2007.
Attractors for Gradient Flows of Nonconvex Functionals and Applications.
Archive for Rational Mechanics and Analysis,
Vol. 187,
Issue. 1,
p.
91.
MIELKE, ALEXANDER
and
ROSSI, RICCARDA
2007.
EXISTENCE AND UNIQUENESS RESULTS FOR A CLASS OF RATE-INDEPENDENT HYSTERESIS PROBLEMS.
Mathematical Models and Methods in Applied Sciences,
Vol. 17,
Issue. 01,
p.
81.
Stefanelli, Ulisse
2008.
The Brezis–Ekeland Principle for Doubly Nonlinear Equations.
SIAM Journal on Control and Optimization,
Vol. 47,
Issue. 3,
p.
1615.
Mielke, Alexander
and
Stefanelli, Ulisse
2011.
Weighted energy-dissipation functionals for gradient flows.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 17,
Issue. 1,
p.
52.
Canuto, Claudio
and
Cimolin, Flavio
2011.
A sweating model for the internal ventilation of a motorcycle helmet.
Computers & Fluids,
Vol. 43,
Issue. 1,
p.
29.
Rossi, Riccarda
Segatti, Antonio
and
Stefanelli, Ulisse
2011.
Global attractors for gradient flows in metric spaces.
Journal de Mathématiques Pures et Appliquées,
Vol. 95,
Issue. 2,
p.
205.
Mielke, Alexander
2011.
Nonlinear PDE’s and Applications.
Vol. 2028,
Issue. ,
p.
87.
Mielke, Alexander
Rossi, Riccarda
and
Savaré, Giuseppe
2012.
Variational Convergence of Gradient Flows and Rate-Independent Evolutions in Metric Spaces.
Milan Journal of Mathematics,
Vol. 80,
Issue. 2,
p.
381.
KNEES, DOROTHEE
ROSSI, RICCARDA
and
ZANINI, CHIARA
2013.
A VANISHING VISCOSITY APPROACH TO A RATE-INDEPENDENT DAMAGE MODEL.
Mathematical Models and Methods in Applied Sciences,
Vol. 23,
Issue. 04,
p.
565.
Barrett, J.W.
Garcke, H.
and
Nürnberg, R.
2013.
On the stable discretization of strongly anisotropic phase field models with applications to crystal growth.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 93,
Issue. 10-11,
p.
719.
Garcke, Harald
2013.
Curvature Driven Interface Evolution.
Jahresbericht der Deutschen Mathematiker-Vereinigung,
Vol. 115,
Issue. 2,
p.
63.
Mielke, Alexander
Rossi, Riccarda
and
Savaré, Giuseppe
2013.
Nonsmooth analysis of doubly nonlinear evolution equations.
Calculus of Variations and Partial Differential Equations,
Vol. 46,
Issue. 1-2,
p.
253.
Pardoux, Etienne
and
Răşcanu, Aurel
2014.
Stochastic Differential Equations, Backward SDEs, Partial Differential Equations.
Vol. 69,
Issue. ,
p.
517.
Răşcanu, Aurel
and
Rotenstein, Eduard
2014.
A non-convex setup for multivalued differential equations driven by oblique subgradients.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 111,
Issue. ,
p.
82.
Negri, Matteo
2014.
Quasi-static rate-independent evolutions: characterization, existence, approximation and application to fracture mechanics.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 20,
Issue. 4,
p.
983.
Pardoux, Etienne
and
Răşcanu, Aurel
2014.
Stochastic Differential Equations, Backward SDEs, Partial Differential Equations.
Vol. 69,
Issue. ,
p.
353.
Pardoux, Etienne
and
Răşcanu, Aurel
2014.
Stochastic Differential Equations, Backward SDEs, Partial Differential Equations.
Vol. 69,
Issue. ,
p.
73.
Pardoux, Etienne
and
Răşcanu, Aurel
2014.
Stochastic Differential Equations, Backward SDEs, Partial Differential Equations.
Vol. 69,
Issue. ,
p.
229.
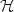 \[
\begin{cases}
u'(t)+ \partial_{\ell}\phi(u(t))\ni f(t)
&\text{{\it a.e.}\ in }(0,T),
u(0)=u_0,
\end{cases}
\]
\[
\begin{cases}
u'(t)+ \partial_{\ell}\phi(u(t))\ni f(t)
&\text{{\it a.e.}\ in }(0,T),
u(0)=u_0,
\end{cases}
\]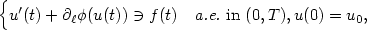 where $\phi: \mathcal{H} \to (-\infty,+\infty]$
where $\phi: \mathcal{H} \to (-\infty,+\infty]$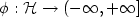 is a proper,
lower semicontinuous functional which is not supposed to be a
(smooth perturbation of a) convex functional and $\partial_{\ell}\phi$
is a proper,
lower semicontinuous functional which is not supposed to be a
(smooth perturbation of a) convex functional and $\partial_{\ell}\phi$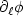 is
(a suitable limiting version of) its subdifferential.
We will present some new existence results for the solutions of the
equation by exploiting a variational approximation
technique, featuring some ideas from the theory of Minimizing Movements
and of Young measures.
Our analysis
is also motivated by some models describing phase transitions
phenomena, leading to
systems of evolutionary PDEs which have a common
underlying gradient flow structure:
in particular, we will focus on
quasistationary models, which exhibit
highly non convex Lyapunov functionals.
is
(a suitable limiting version of) its subdifferential.
We will present some new existence results for the solutions of the
equation by exploiting a variational approximation
technique, featuring some ideas from the theory of Minimizing Movements
and of Young measures.
Our analysis
is also motivated by some models describing phase transitions
phenomena, leading to
systems of evolutionary PDEs which have a common
underlying gradient flow structure:
in particular, we will focus on
quasistationary models, which exhibit
highly non convex Lyapunov functionals.


