Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-23T21:36:49.625Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero-dimensional isomorphic dynamical models

Part of: Topological dynamics

Published online by Cambridge University Press:  11 December 2018

TOMASZ DOWNAROWICZ Open the ORCID record for TOMASZ DOWNAROWICZ [Opens in a new window] ,
LEI JIN ,
WOLFGANG LUSKY  and
YIXIAO QIAO
TOMASZ DOWNAROWICZ
Affiliation:
Faculty of Mathematics and Faculty of Fundamental Problems of Technology, Wrocław University of Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland email Tomasz.Downarowicz@pwr.edu.pl
LEI JIN
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-656 Warszawa, Poland email jinleim@mail.ustc.edu.cn
WOLFGANG LUSKY
Affiliation:
Institut für Mathematik, Universität Paderborn, Warburger Strasse 100, 33098 Paderborn, Germany email lusky@math.uni-paderborn.de
YIXIAO QIAO
Affiliation:
School of Mathematical Sciences, South China Normal University, Guangzhou, Guangdong 510631, China email yxqiao@mail.ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

By an assignment we mean a mapping from a Choquet simplex 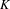$K$ to probability measure-preserving systems obeying some natural restrictions. We prove that if 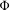$\unicode[STIX]{x1D6F7}$ is an aperiodic assignment on a Choquet simplex 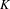$K$ such that the set of extreme points 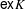$\mathsf{ex}K$ is a countable union 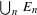$\bigcup _{n}E_{n}$, where each set 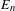$E_{n}$ is compact, zero-dimensional and the restriction of 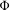$\unicode[STIX]{x1D6F7}$ to the Bauer simplex 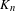$K_{n}$ spanned by 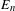$E_{n}$ can be ‘embedded’ in some topological dynamical system, then 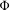$\unicode[STIX]{x1D6F7}$ can be ‘realized’ in a zero-dimensional system.

Keywords

assignmentzero-dimensional systemisomorphic modelmeasure-theoretic isomorphism

MSC classification

Primary: 37B10: Symbolic dynamics 37B40: Topological entropy
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 8 , August 2020 , pp. 2116 - 2130
Check for updates
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boyle, M. and Downarowicz, T.. The entropy theory of symbolic extensions. Invent. Math. 156 (2004), 119–161.10.1007/s00222-003-0335-2CrossRefGoogle Scholar
Boyle, M.. Lower entropy factors of sofic systems. Ergod. Th. & Dynam. Sys. 3 (1983), 541–557.10.1017/S0143385700002133CrossRefGoogle Scholar
Downarowicz, T. and Karpel, O.. Dynamics in dimension zero: a survey. Discrete Cont. Dynam. Syst. A 38(3) (2018), 1033–1062.10.3934/dcds.2018044CrossRefGoogle Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Contemp. Math. 385 (2005), 7–38.10.1090/conm/385/07188CrossRefGoogle Scholar
Downarowicz, T.. Minimal models for noninvertible and not uniquely ergodic systems. Israel J. Math. 156 (2006), 93–124.10.1007/BF02773826CrossRefGoogle Scholar
Downarowicz, T.. Faces of simplexes of invariant measures. Israel J. Math. 165(1) (2008), 189–210.10.1007/s11856-008-1009-yCrossRefGoogle Scholar
Downarowicz, T.. Entropy in Dynamical Systems. Cambridge University Press, Cambridge, 2011.10.1017/CBO9780511976155CrossRefGoogle Scholar
Downarowicz, T.. The Choquet simplex of invariant measures for minimal flows. Israel J. Math. 74 (1991), 241–256.10.1007/BF02775789CrossRefGoogle Scholar
Downarowicz, T. and Serafin, J.. Possible entropy functions. Israel J. Math. 135 (2003), 221–250.10.1007/BF02776059CrossRefGoogle Scholar
Fonf, V. P., Lindenstrauss, J. and Phelps, R. R.. Infinite Dimensional Convexity (Handbook of the Geometry of Banach Spaces, 1). North-Holland, Amsterdam, 2001, pp. 599–670.Google Scholar
Kornfeld, I. and Ormes, N.. Topological realizations of families of ergodic automorphisms, multitowers and orbit equivalence. Israel J. Math. 155 (2006), 335–357.10.1007/BF02773959CrossRefGoogle Scholar
Lazar, A. J.. Spaces of affine continuous functions on simplices. Trans. Amer. Math. Soc. 134 (1968), 503–525.10.1090/S0002-9947-1968-0233188-2CrossRefGoogle Scholar
Lindenstrauss, E.. Mean dimension, small entropy factors and an embedding theorem. Publ. Math. Inst. Hautes Études Sci. 89 (1999), 227–262.10.1007/BF02698858CrossRefGoogle Scholar
Lindenstrauss, J., Olsen, G. and Sternfeld, Y.. The Poulsen simplex. Ann. Inst. Fourier (Grenoble) 28 (1978), 91–114.10.5802/aif.682CrossRefGoogle Scholar
Phelps, R. R.. Lectures on Choquet’s Theorem (Lecture Notes in Mathematics, 1757). Springer, Berlin, 2001.10.1007/b76887CrossRefGoogle Scholar