No CrossRef data available.
Article contents
Vanishing of cohomology and parameter rigidity of actions of solvable Lie groups, II
Published online by Cambridge University Press: 03 November 2020
Abstract
Let
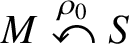 $M\stackrel {\rho _0}{\curvearrowleft }S$
be a
$M\stackrel {\rho _0}{\curvearrowleft }S$
be a
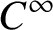 $C^\infty $
locally free action of a connected simply connected solvable Lie group S on a closed manifold M. Roughly speaking,
$C^\infty $
locally free action of a connected simply connected solvable Lie group S on a closed manifold M. Roughly speaking,
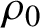 $\rho _0$
is parameter rigid if any
$\rho _0$
is parameter rigid if any
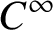 $C^\infty $
locally free action of S on M having the same orbits as
$C^\infty $
locally free action of S on M having the same orbits as
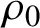 $\rho _0$
is
$\rho _0$
is
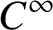 $C^\infty $
conjugate to
$C^\infty $
conjugate to
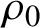 $\rho _0$
. In this paper we prove two types of result on parameter rigidity.
$\rho _0$
. In this paper we prove two types of result on parameter rigidity.
First let G be a connected semisimple Lie group with finite center of real rank at least
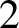 $2$
without compact factors nor simple factors locally isomorphic to
$2$
without compact factors nor simple factors locally isomorphic to
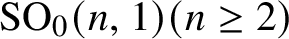 $\mathop {\mathrm {SO}}\nolimits _0(n,1)(n\,{\geq}\, 2)$
or
$\mathop {\mathrm {SO}}\nolimits _0(n,1)(n\,{\geq}\, 2)$
or
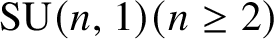 $\mathop {\mathrm {SU}}\nolimits (n,1)(n\geq 2)$
, and let
$\mathop {\mathrm {SU}}\nolimits (n,1)(n\geq 2)$
, and let
 $\Gamma $
be an irreducible cocompact lattice in G. Let
$\Gamma $
be an irreducible cocompact lattice in G. Let
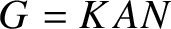 $G=KAN$
be an Iwasawa decomposition. We prove that the action
$G=KAN$
be an Iwasawa decomposition. We prove that the action
 $\Gamma \backslash G\curvearrowleft AN$
by right multiplication is parameter rigid. One of the three main ingredients of the proof is the rigidity theorems of Pansu, and Kleiner and Leeb on the quasi-isometries of Riemannian symmetric spaces of non-compact type.
$\Gamma \backslash G\curvearrowleft AN$
by right multiplication is parameter rigid. One of the three main ingredients of the proof is the rigidity theorems of Pansu, and Kleiner and Leeb on the quasi-isometries of Riemannian symmetric spaces of non-compact type.
Secondly we show that if
 $M\stackrel {\rho _0}{\curvearrowleft }S$
is parameter rigid, then the zeroth and first cohomology of the orbit foliation of
$M\stackrel {\rho _0}{\curvearrowleft }S$
is parameter rigid, then the zeroth and first cohomology of the orbit foliation of
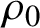 $\rho _0$
with certain coefficients must vanish. This is a partial converse to the results in the author’s [Vanishing of cohomology and parameter rigidity of actions of solvable Lie groups. Geom. Topol. 21(1) (2017), 157–191], where we saw sufficient conditions for parameter rigidity in terms of vanishing of the first cohomology with various coefficients.
$\rho _0$
with certain coefficients must vanish. This is a partial converse to the results in the author’s [Vanishing of cohomology and parameter rigidity of actions of solvable Lie groups. Geom. Topol. 21(1) (2017), 157–191], where we saw sufficient conditions for parameter rigidity in terms of vanishing of the first cohomology with various coefficients.
- Type
- Original Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press





