Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-19T10:46:24.544Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniformity of Lyapunov exponents for non-invertible matrices

Part of: Classical measure theory Random dynamical systems

Published online by Cambridge University Press:  26 February 2019

DE-JUN FENG ,
CHIU-HONG LO  and
SHUANG SHEN
DE-JUN FENG
Affiliation:
Department of Mathematics, The Chinese University of Hong Kong, Shatin, Hong Kong email djfeng@math.cuhk.edu.hk, chlo@math.cuhk.edu.hk
CHIU-HONG LO
Affiliation:
Department of Mathematics, The Chinese University of Hong Kong, Shatin, Hong Kong email djfeng@math.cuhk.edu.hk, chlo@math.cuhk.edu.hk
SHUANG SHEN
Affiliation:
Department of Mathematics, The Chinese University of Hong Kong, Shatin, Hong Kong email djfeng@math.cuhk.edu.hk, chlo@math.cuhk.edu.hk Department of Applied Mathematics, Northwestern Polytechnical University, Xi’an, Shaanxi, 710129, P.R. China email gjdyyss@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 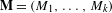$\mathbf{M}=(M_{1},\ldots ,M_{k})$ be a tuple of real 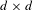$d\times d$ matrices. Under certain irreducibility assumptions, we give checkable criteria for deciding whether 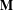$\mathbf{M}$ possesses the following property: there exist two constants 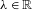$\unicode[STIX]{x1D706}\in \mathbb{R}$ and 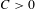$C>0$ such that for any 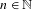$n\in \mathbb{N}$ and any 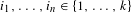$i_{1},\ldots ,i_{n}\in \{1,\ldots ,k\}$, either 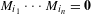$M_{i_{1}}\cdots M_{i_{n}}=\mathbf{0}$ or $C^{-1}e^{\unicode[STIX]{x1D706}n}\leq \Vert M_{i_{1}}\cdots M_{i_{n}}\Vert \leq Ce^{\unicode[STIX]{x1D706}n}$, where $\Vert \cdot \Vert$ is a matrix norm. The proof is based on symbolic dynamics and the thermodynamic formalism for matrix products. As applications, we are able to check the absolute continuity of a class of overlapping self-similar measures on 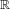$\mathbb{R}$, the absolute continuity of certain self-affine measures in 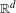$\mathbb{R}^{d}$ and the dimensional regularity of a class of sofic affine-invariant sets in the plane.

Keywords

Lyapunov exponentsmatrix productsuniformity

MSC classification

Primary: 37H15: Multiplicative ergodic theory, Lyapunov exponents
Secondary: 28A80: Fractals
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2399 - 2433
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barral, J. and Feng, D.-J.. Multifractal formalism for almost all self-affine measures. Comm. Math. Phys. 318(2) (2013), 473–504.Google Scholar
Bedford, T.. Crinkly curves, Markov partitions and dimension. PhD Thesis, University of Warwick, 1984.Google Scholar
Blondel, V. D. and Tsitsiklis, J. N.. When is a pair of matrices mortal? Inform. Process. Lett. 63(5) (1997), 283–286.Google Scholar
Blondel, V. D. and Tsitsiklis, J. N.. The boundedness of all products of a pair of matrices is undecidable. Systems Control Lett. 41(2) (2000), 135–140.Google Scholar
Blondel, V. D. and Tsitsiklis, J. N.. A survey of computational complexity results in systems and control. Automatica J. IFAC 36(9) (2000), 1249–1274.Google Scholar
Cao, Y.-L., Feng, D.-J. and Huang, W.. The thermodynamic formalism for sub-additive potentials. Discrete Contin. Dyn. Syst. 20(3) (2008), 639–657.Google Scholar
Cassaigne, J., Halava, V., Harju, T. and Nicolas, F.. Tighter undecidability bounds for matrix mortality, zero-in-the-corner problems, and more. Preprint, 2014, arXiv:1404.0644.Google Scholar
Deng, Q.-R., He, X.-G. and Lau, K.-S.. Self-affine measures and vector-valued representations. Studia Math. 188(3) (2008), 259–286.Google Scholar
Falconer, K. J.. Fractal Geometry: Mathematical Foundations and Applications, 2nd edn. John Wiley & Sons, Inc., Hoboken, NJ, 2003.Google Scholar
Fan, A.-H., Lau, K.-S. and Rao, H.. Relationships between different dimensions of a measure. Monatsh. Math. 135(3) (2002), 191–201.Google Scholar
Feng, D.-J.. Smoothness of the L q-spectrum of self-similar measures with overlaps. J. Lond. Math. Soc. (2) 68(1) (2003), 102–118.Google Scholar
Feng, D.-J.. The variational principle for products of non-negative matrices. Nonlinearity 17(2) (2004), 447–457.Google Scholar
Feng, D.-J.. Equilibrium states for factor maps between subshifts. Adv. Math. 226(3) (2011), 2470–2502.Google Scholar
Feng, D.-J. and Hu, H.. Dimension theory of iterated function systems. Comm. Pure Appl. Math. 62(11) (2009), 1435–1500.Google Scholar
Feng, D.-J. and Käenmäki, A.. Equilibrium states of the pressure function for products of matrices. Discrete Contin. Dyn. Syst. 30(3) (2011), 699–708.Google Scholar
Feng, D.-J. and Lau, K.-S.. The pressure function for products of non-negative matrices. Math. Res. Lett. 9(2–3) (2002), 363–378.Google Scholar
Feng, D.-J. and Lau, K.-S.. Multifractal formalism for self-similar measures with weak separation condition. J. Math. Pures Appl. (9) 92(4) (2009), 407–428.Google Scholar
Hare, K. E., Hare, K. G. and Ng, M. K. S.. Local dimensions of measures of finite type II — measures without full support and with non-regular probabilities. Canad. J. Math. 70(4) (2018), 824–867.Google Scholar
Hare, K. G., Morris, I. D., Sidorov, N. and Theys, J.. An explicit counterexample to the Lagarias–Wang finiteness conjecture. Adv. Math. 226(6) (2011), 4667–4701.Google Scholar
Horn, R. A. and Johnson, C. R.. Matrix Analysis. Cambridge University Press, Cambridge, 1985.Google Scholar
Huang, W.. Private communication, 2015.Google Scholar
Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30(5) (1981), 713–747.Google Scholar
Jia, R.-Q., Lau, K.-S. and Zhou, D.-X.. L p solutions of refinement equations. J. Fourier Anal. Appl. 7(2) (2001), 143–167.Google Scholar
Jungers, R.. The Joint Spectral Radius: Theory and Applications (Lecture Notes in Control and Information Sciences, 385). Springer, Berlin, 2009.Google Scholar
Käenmäki, A.. On natural invariant measures on generalised iterated function systems. Ann. Acad. Sci. Fenn. Math. 29(2) (2004), 419–458.Google Scholar
Kenyon, R. and Peres, Y.. Hausdorff dimensions of sofic affine-invariant sets. Israel J. Math. 94 (1996), 157–178.Google Scholar
Kenyon, R. and Peres, Y.. Measures of full dimension on affine-invariant sets. Ergod. Th. & Dynam. Sys. 16(2) (1996), 307–323.Google Scholar
Lagarias, J. C. and Wang, Y.. The finiteness conjecture for the generalized spectral radius of a set of matrices. Linear Algebra Appl. 214 (1995), 17–42.Google Scholar
Lagarias, J. C. and Wang, Y.. Integral self-affine tiles in Rn. I. Standard and nonstandard digit sets. J. Lond. Math. Soc. (2) 54(1) (1996), 161–179.Google Scholar
Lalley, S. P.. Random series in powers of algebraic integers: Hausdorff dimension of the limit distribution. J. Lond. Math. Soc. (2) 57(3) (1998), 629–654.Google Scholar
Lau, K.-S. and Ngai, S.-M.. Multifractal measures and a weak separation condition. Adv. Math. 141(1) (1999), 45–96.Google Scholar
Lau, K.-S., Ngai, S.-M. and Rao, H.. Iterated function systems with overlaps and self-similar measures. J. Lond. Math. Soc. (2) 63(1) (2001), 99–116.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Lo, C. H.. Dimensional regularity of some sofic affine sets. Master Thesis, The Chinese University of Hong Kong, 2012.Google Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces (Cambridge Studies in Advanced Mathematics, 44). Cambridge University Press, Cambridge, 1995.Google Scholar
McMullen, C.. The Hausdorff dimension of general Sierpiński carpets. Nagoya Math. J. 96 (1984), 1–9.Google Scholar
Morris, I. D.. Ergodic properties of matrix equilibrium states. Ergod. Th. & Dynam. Sys. 38(6) (2018), 2295–2320.Google Scholar
Ngai, S.-M. and Wang, Y.. Hausdorff dimension of self-similar sets with overlaps. J. Lond. Math. Soc. (2) 63(3) (2001), 655–672.Google Scholar
Nguyen, N.. Iterated function systems of finite type and the weak separation property. Proc. Amer. Math. Soc. 130(2) (2002), 483–487 (electronic).Google Scholar
Omladič, M. and Radjavi, H.. Irreducible semigroups with multiplicative spectral radius. Linear Algebra Appl. 251 (1997), 59–72.Google Scholar
Parry, W.. Intrinsic Markov chains. Trans. Amer. Math. Soc. 112 (1964), 55–66.Google Scholar
Paterson, M. S.. Unsolvability in 3 × 3 matrices. Stud. Appl. Math. 49 (1970), 105–107.Google Scholar
Peres, Y., Schlag, W. and Solomyak, B.. Sixty years of Bernoulli convolutions. Fractal Geometry and Stochastics, II (Greifswald/Koserow, 1998) (Progress in Probability, 46). Birkhäuser, Basel, 2000, pp. 39–65.Google Scholar
Popov, A. I.. On matrix semigroups bounded above and below. Linear Algebra Appl. 438(11) (2013), 4439–4447.Google Scholar
Protasov, V. Y.. Refinement equations with nonnegative coefficients. J. Fourier Anal. Appl. 6(1) (2000), 55–78.Google Scholar
Protasov, V. Y.. When do several linear operators share an invariant cone? Linear Algebra Appl. 433(4) (2010), 781–789.Google Scholar
Protasov, V. Y. and Voynov, A. S.. Matrix semigroups with constant spectral radius. Linear Algebra Appl. 513 (2017), 376–408.Google Scholar
Rockafellar, R. T.. Convex Analysis (Princeton Mathematical Series, No. 28). Princeton University Press, Princeton, NJ, 1970.Google Scholar
Ruiz, V.. Dimension of homogeneous rational self-similar measures with overlaps. J. Math. Anal. Appl. 353(1) (2009), 350–361.Google Scholar
Shmerkin, P.. Overlapping self-affine sets. Indiana Univ. Math. J. 55(4) (2006), 1291–1331.Google Scholar
Shmerkin, P.. On the exceptional set for absolute continuity of Bernoulli convolutions. Geom. Funct. Anal. 24(3) (2014), 946–958.Google Scholar
Shmerkin, P. and Solomyak, B.. Absolute continuity of self-similar measures, their projections and convolutions. Trans. Amer. Math. Soc. 368(7) (2016), 5125–5151.Google Scholar
Solomyak, B.. On the random series ∑ ±𝜆n (an Erdős problem). Ann. of Math. (2) 142(3) (1995), 611–625.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.Google Scholar
Zerner, M. P. W.. Weak separation properties for self-similar sets. Proc. Amer. Math. Soc. 124(11) (1996), 3529–3539.Google Scholar
Zhou, D.-X.. The p-norm joint spectral radius for even integers. Methods Appl. Anal. 5(1) (1998), 39–54.Google Scholar