Hostname: page-component-7bb8b95d7b-qxsvm Total loading time: 0 Render date: 2024-09-27T04:36:55.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Stretched-exponential mixing for 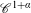$\mathscr{C}^{1+\unicode[STIX]{x1D6FC}}$ skew products with discontinuities

Published online by Cambridge University Press:  22 July 2015

PEYMAN ESLAMI
PEYMAN ESLAMI*
Affiliation:
Dipartimento di Matematica, II Università di Roma (Tor Vergata), Via della Ricerca Scientifica, 00133 Roma, Italy email eslami@mat.uniroma2.it
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the skew product 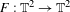$F:\mathbb{T}^{2}\rightarrow \mathbb{T}^{2}$, 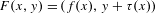$F(x,y)=(f(x),y+\unicode[STIX]{x1D70F}(x))$, where 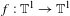$f:\mathbb{T}^{1}\rightarrow \mathbb{T}^{1}$ is a piecewise 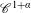$\mathscr{C}^{1+\unicode[STIX]{x1D6FC}}$ expanding map on a countable partition and 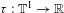$\unicode[STIX]{x1D70F}:\mathbb{T}^{1}\rightarrow \mathbb{R}$ is piecewise 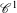$\mathscr{C}^{1}$. It is shown that if $\unicode[STIX]{x1D70F}$ is not Lipschitz-cohomologous to a piecewise constant function on the joint partition of 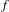$f$ and $\unicode[STIX]{x1D70F}$, then $F$ is mixing at a stretched-exponential rate.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 1 , February 2017 , pp. 146 - 175
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A., Gouëzel, S. and Yoccoz, J.-C.. Exponential mixing for the Teichmüller flow. Publ. Math. Inst. Hautes Études Sci. 104 (2006), 143–211.CrossRefGoogle Scholar
Baladi, V. and Liverani, C.. Exponential decay of correlations for piecewise cone hyperbolic contact flows. Comm. Math. Phys. 314(3) (2012), 689–773.Google Scholar
Baladi, V. and Vallée, B.. Exponential decay of correlations for surface semi-flows without finite Markov partitions. Proc. Amer. Math. Soc. 133(3) (2005), 865–874 (electronic).Google Scholar
Boyarsky, A. and Góra, P.. Laws of Chaos, Invariant Measures and Dynamical Systems in One Dimension (Probability and its Applications) . Birkhäuser Boston, Inc., Boston, MA, 1997.Google Scholar
Butterley, O.. Area expanding C1+𝛼 suspension semiflows. Comm. Math. Phys. 325(2) (2014), 803–820.Google Scholar
Butterley, O. and Eslami, P.. Exponential mixing for skew products with discontinuities. Preprint, 2014,arXiv:1405.7008.Google Scholar
Chernov, N.. A stretched exponential bound on time correlations for billiard flows. J. Stat. Phys. 127(1) (2007), 21–50.Google Scholar
Chernov, N. and Dolgopyat, D.. Particle drift in self-similar billiards. Ergod. Th. & Dynam. Sys. 28(2) (2008), 389–403.Google Scholar
Chernov, N. and Dolgopyat, D.. Brownian Brownian motion. I (Memoirs of the American Mathematical Society, 198) . American Mathematical Society, Providence, RI, 2009.Google Scholar
Chernov, N. and Markarian, R.. Chaotic Billiards (Mathematical Surveys and Monographs, 127) . American Mathematical Society, Providence, RI, 2006.Google Scholar
Chernov, N. I.. Markov approximations and decay of correlations for Anosov flows. Ann. of Math. (2) 147(2) (1998), 269–324.Google Scholar
Dolgopyat, D.. On decay of correlations in Anosov flows. Ann. of Math. (2) 147(2) (1998), 357–390.Google Scholar
Dolgopyat, D.. On differentiability of SRB states for partially hyperbolic systems. Invent. Math. 155(2) (2004), 389–449.Google Scholar
Ionescu Tulcea, C. T. and Marinescu, G.. Théorie ergodique pour des classes d’opérations non complètement continues. Ann. of Math. (2) 52 (1950), 140–147.Google Scholar
Keller, G.. Generalized bounded variation and applications to piecewise monotonic transformations. Z. Wahrsch. Verw. Gebiete 69(3) (1985), 461–478.Google Scholar
Liverani, C.. Decay of correlations for piecewise expanding maps. J. Stat. Phys. 78(3–4) (1995), 1111–1129.Google Scholar
Liverani, C.. On contact Anosov flows. Ann. of Math. (2) 159(3) (2004), 1275–1312.Google Scholar
Obayashi, I.. Exponential decay of correlations for surface semiflows with an expanding direction. Kyoto J. Math. 49(2) (2009), 427–440.Google Scholar
Peres, Y. and Solomyak, B.. Absolute continuity of Bernoulli convolutions, a simple proof. Math. Res. Lett. 3(2) (1996), 231–239.Google Scholar
Pollicott, M.. On the rate of mixing of Axiom A flows. Invent. Math. 81(3) (1985), 413–426.Google Scholar
Pollicott, M.. On the mixing of Axiom A attracting flows and a conjecture of Ruelle. Ergod. Th. & Dynam. Sys. 19(2) (1999), 535–548.Google Scholar
Ruelle, D.. Flots qui ne mélangent pas exponentiellement. C. R. Acad. Sci., Paris I 296(4) (1983), 191–193.Google Scholar
Sarig, O.. Subexponential decay of correlations. Invent. Math. 150(3) (2002), 629–653.Google Scholar
Tsujii, M.. Fat solenoidal attractors. Nonlinearity 14(5) (2001), 1011–1027.Google Scholar
Tsujii, M.. Decay of correlations in suspension semi-flows of angle-multiplying maps. Ergod. Th. & Dynam. Sys. 28(1) (2008), 291–317.Google Scholar
Young, L.-S.. Statistical properties of dynamical systems with some hyperbolicity. Ann. of Math. (2) 147(3) (1998), 585–650.Google Scholar
Young, L.-S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar