Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-25T12:55:13.357Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic approximation of Lyapunov exponents for Banach cocycles

Published online by Cambridge University Press:  20 June 2017

BORIS KALININ  and
VICTORIA SADOVSKAYA
BORIS KALININ
Affiliation:
Department of Mathematics, The Pennsylvania State University, University Park, PA 16802, USA email kalinin@psu.edu, sadovskaya@psu.edu
VICTORIA SADOVSKAYA
Affiliation:
Department of Mathematics, The Pennsylvania State University, University Park, PA 16802, USA email kalinin@psu.edu, sadovskaya@psu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider group-valued cocycles over dynamical systems. The base system is a homeomorphism 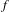$f$ of a metric space satisfying a closing property, for example a hyperbolic dynamical system or a subshift of finite type. The cocycle 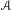$A$ takes values in the group of invertible bounded linear operators on a Banach space and is Hölder continuous. We prove that upper and lower Lyapunov exponents of 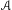$A$ with respect to an ergodic invariant measure $\unicode[STIX]{x1D707}$ can be approximated in terms of the norms of the values of 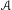$A$ on periodic orbits of 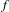$f$. We also show that these exponents cannot always be approximated by the exponents of 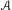$A$ with respect to measures on periodic orbits. Our arguments include a result of independent interest on construction and properties of a Lyapunov norm for the infinite-dimensional setting. As a corollary, we obtain estimates of the growth of the norm and of the quasiconformal distortion of the cocycle in terms of the growth at the periodic points o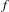f $f$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 3 , March 2019 , pp. 689 - 706
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barreira, L. and Pesin, Ya.. Nonuniform Hyperbolicity: Dynamics of Systems with Nonzero Lyapunov Exponents (Encyclopedia of Mathematics and its Applications, 115) . Cambridge University Press, New York, 2007.Google Scholar
Grabarnik, G. and Guysinsky, M.. Livšic theorem for Banach rings. Discrete Contin. Dyn. Syst. 37(8) (2017), 4379–4390.Google Scholar
Gouëzel, S. and Karlsson, A.. Subadditive and multiplicative ergodic theorems. Preprint.Google Scholar
Gurvits, L.. Stability of discrete linear inclusion. Linear Algebra Appl. 231 (1995), 47–85.Google Scholar
Kalinin, B.. Livsic theorem for matrix cocycles. Ann. of Math. (2) 173(2) (2011), 1025–1042.Google Scholar
Karlsson, A. and Margulis, G.. A multiplicative ergodic theorem and nonpositively curved spaces. Comm. Math. Phys. 208 (1999), 107–123.Google Scholar
Kalinin, B. and Sadovskaya, V.. Cocycles with one exponent over partially hyperbolic systems. Geom. Dedicata 167(1) (2013), 167–188.Google Scholar
Kalinin, B. and Sadovskaya, V.. Boundedness, compactness, and invariant norms for Banach cocycles over hyperbolic systems. Proc. Amer. Math. Soc., to appear.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54) . Cambridge University Press, Cambridge, 1995.Google Scholar
Lian, Z. and Lu, K.. Lyapunov exponents and invariant manifolds for random dynamical systems in a Banach space. Mem. Amer. Math. Soc. 206(967) (2010).Google Scholar
Lian, Z. and Young, L. S.. Lyapunov exponents, periodic orbits, and horseshoes for semiflows on Hilbert spaces. J. Amer. Math. Soc. 25(3) (2012), 637–665.Google Scholar
Morris, I.. The generalised Berger–Wang formula and the spectral radius of linear cocycles. J. Funct. Anal. 262 (2012), 811–824.Google Scholar
Sadovskaya, V.. Fiber bunching and cohomology for Banach cocycles. Discrete Contin. Dyn. Syst. 37(9) (2017).Google Scholar
Schreiber, S. J.. On growth rates of subadditive functions for semi-flows. J. Differential Equations 148 (1998), 334–350.Google Scholar