Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-19T06:00:51.923Z Has data issue: false hasContentIssue false
  • English
  • Français

On shrinking targets for piecewise expanding interval maps

Published online by Cambridge University Press:  25 August 2015

TOMAS PERSSON  and
MICHAŁ RAMS
TOMAS PERSSON
Affiliation:
Centre for Mathematical Sciences, Lund University, Box 118, 22100 Lund, Sweden email tomasp@maths.lth.se
MICHAŁ RAMS
Affiliation:
Instytut Matematyczny, Polska Akademia Nauk, ul. Sniadeckich 8, 00-656 Warszawa, Poland email rams@impan.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

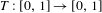For a map $T:[0,1]\rightarrow [0,1]$ with an invariant measure $\unicode[STIX]{x1D707}$, we study, for a $\unicode[STIX]{x1D707}$-typical $x$, the set of points $y$ such that the inequality 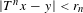$|T^{n}x-y|<r_{n}$ is satisfied for infinitely many $n$. We give a formula for the Hausdorff dimension of this set, under the assumption that $T$ is piecewise expanding and 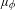$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D719}}$ is a Gibbs measure. In some cases we also show that the set has a large intersection property.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 2 , April 2017 , pp. 646 - 663
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50) . American Mathematical Society, Providence, RI, 1997.Google Scholar
Aaronson, J. and Denker, M.. Upper bounds for ergodic sums of infinite measure preserving transformations. Trans. Amer. Math. Soc. 319(1) (1990), 101–138.CrossRefGoogle Scholar
Falconer, K.. Sets with large intersection properties. J. Lond. Math. Soc. (2) 49(2) (1994), 267–280.CrossRefGoogle Scholar
Fan, A.-H., Schmeling, J. and Troubetzkoy, S.. A multifractal mass transference principle for Gibbs measures with applications to dynamical Diophantine approximation. Proc. Lond. Math. Soc. (3) 107 (2013), 1173–1219.Google Scholar
Hofbauer, F.. Local dimension for piecewise monotonic maps on the interval. Ergod. Th. & Dynam. Sys. 15(6) (1995), 1119–1142.CrossRefGoogle Scholar
Li, B., Wang, B.-W., Wu, J. and Xu, J.. The shrinking target problem in the dynamical system of continued fractions. Proc. Lond. Math. Soc. (3) 108 (2014), 159–186.CrossRefGoogle Scholar
Liao, L. and Seuret, S.. Diophantine approximation by orbits of expanding Markov maps. Ergod. Th. & Dynam. Sys. 33(2) (2013), 585–608.CrossRefGoogle Scholar
Liverani, C.. Decay of correlations for piecewise expanding maps. J. Stat. Phys. 78(3–4) (1995), 1111–1129.Google Scholar
Liverani, C., Saussol, B. and Vaienti, S.. Conformal measure and decay of correlation for covering weighted systems. Ergod. Th. & Dynam. Sys. 18(6) (1998), 1399–1420.Google Scholar
Persson, T.. A note on random coverings of Tori. Bull. Lond. Math. Soc. 47(1) (2015), 7–12.CrossRefGoogle Scholar
Persson, T. and Reeve, H.. A Frostman type lemma for sets with large intersections, and an application to Diophantine approximation. Proc. Edinburgh Math. Soc. 58(2) (2015), 521–542.CrossRefGoogle Scholar
Rychlik, M.. Bounded variation and invariant measures. Studia Math. 76(1) (1983), 69–80.CrossRefGoogle Scholar