Hostname: page-component-5c6d5d7d68-wtssw Total loading time: 0 Render date: 2024-08-16T05:42:57.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective mixing and counting in Bruhat–Tits trees

Published online by Cambridge University Press:  04 July 2016

SANGHOON KWON
SANGHOON KWON*
Affiliation:
Department of Mathematical Science, Seoul National University, 1 Gwanak-ro, Gwanak-gu, 08826 Seoul, Korea email sanghoon.kwon@snu.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 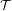${\mathcal{T}}$ be a locally finite tree, 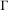$\unicode[STIX]{x1D6E4}$ be a discrete subgroup of 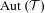$\,\operatorname{Aut}\,({\mathcal{T}})$ and 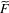$\widetilde{F}$ be a 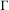$\unicode[STIX]{x1D6E4}$-invariant potential. Suppose that the length spectrum of 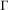$\unicode[STIX]{x1D6E4}$ is not arithmetic. In this case, we prove the exponential mixing property of the geodesic translation map 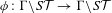$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D6E4}\backslash S{\mathcal{T}}\rightarrow \unicode[STIX]{x1D6E4}\backslash S{\mathcal{T}}$ with respect to the measure 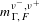$m_{\unicode[STIX]{x1D6E4},F}^{\unicode[STIX]{x1D708}^{-},\unicode[STIX]{x1D708}^{+}}$ under the assumption that 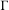$\unicode[STIX]{x1D6E4}$ is full and 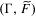$(\unicode[STIX]{x1D6E4},\widetilde{F})$ has a weighted spectral gap. We also obtain the effective formula for the number of 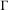$\unicode[STIX]{x1D6E4}$-orbits with weights in a Bruhat–Tits tree 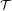${\mathcal{T}}$ of an algebraic group.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 1 , February 2018 , pp. 257 - 283
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bass, H.. Covering theory for graphs of groups. J. Pure Appl. Algebra 89 (1993), 3–47.Google Scholar
Bekka, B. and Lubotzky, A.. Lattices with and lattices without spectral gap. Groups Geom. Dyn. 5 (2011), 251–264.CrossRefGoogle Scholar
Borthwick, D.. Spectral Theory of Infinite-Area Hyperbolic Surfaces (Progress in Mathematics, 256) . Birkhäuser Boston, Inc., Boston, MA, 2007.Google Scholar
Broise-Alamichel, A. and Paulin, F.. Sur le codage du flot géodésique dans un arbre. Ann. Fac. Sci. Toulouse 16 (2007), 477–527.CrossRefGoogle Scholar
Broise-Alamichel, A., Parkkonen, J. and Paulin, F.. Equidistribution in quantum graphs and applications to non-Archimedian Diophantine approximation, In preparation.Google Scholar
Burger, M. and Mozes, S.. CAT(- 1)-spaces, divergence groups and their commensurators. J. Amer. Math. Soc. 9(1) (1996), 57–93.CrossRefGoogle Scholar
Coornaert, M. and Papadopoulos, A.. Upper and lower bounds for the mass of the geodesic flow on graphs. Math. Proc. Cambridge Philos. Soc. 121(3) (1997), 479–493.Google Scholar
Duke, W., Rudnick, Z. and Sarnak, P.. Density of integer points on affine homogeneous varieties. Duke Math. J. 71(1) (1993), 143–179.CrossRefGoogle Scholar
Eskin, A. and McMullen, C.. Mixing, counting, and equidistribution in Lie groups. Duke Math. J. 71(1) (1993), 181–209.Google Scholar
Gorodnik, A. and Nevo, A.. Counting lattice points. J. Reine Angew. Math. 663 (2012), 127–176.Google Scholar
Mohammadi, A. and Oh, H.. Matrix coefficients, counting and primes for orbits of geometrically finite groups. J. Eur. Math. Soc. (JEMS) 17(4) (2015), 837–897.Google Scholar
Meyn, S. and Tweedie, R.. Markov Chains and Stochastic Stability. Cambridge University Press, Cambridge, 2009.Google Scholar
Oh, H. and Shah, N.. Equidistribution and counting for orbits of geometrically finite hyperbolic groups. J. Amer. Math. Soc. 26 (2013), 511–562.CrossRefGoogle Scholar
Oh, H. and Winter, D.. Uniform exponential mixing and resonance free regions for convex cocompact congruence subgroups of $\text{SL}_{2}(\mathbb{Z})$ , To appear in J. Amer. Math. Soc., arXiv:1410.4401.Google Scholar
Paulin, F.. Groupes géométriquement finis d’automorphismes d’arbres et approximation Diophantienne dans les arbres. Manuscripta Math. 113 (2004), 1–23.Google Scholar
Paulin, F., Pollicott, M. and Schapira, B.. Equilibrium States in Negative Curvature (Astérisque, 373) . Société Mathématique de France, Marseille, 2015.Google Scholar
Roblin, T.. Ergodicité et équidistribution en courbure négative. (Mémoires de la Société Mathématique de France, 95). Société Mathématique de France, Paris, 2003.Google Scholar
Serre, J. P.. Trees (Springer Monographs in Mathematics) . Springer, Berlin, 2003.Google Scholar
Sullivan, D.. The density at infinity of a discrete group of hyperbolic motions. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 171–202.CrossRefGoogle Scholar
Tits, J.. Reductive groups over local fields. Automorphic Forms, Representations and L-Functions (Proceedings of Symposia in Pure Mathematics, 33) . American Mathematical Society, Providence, RI, 1979.Google Scholar
Young, L. S.. Recurrent times and rates of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar