Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T17:23:18.714Z Has data issue: false hasContentIssue false
  • English
  • Français

Chaos and frequent hypercyclicity for weighted shifts

Part of: General theory of linear operators Topological linear spaces and related structures Special classes of linear operators

Published online by Cambridge University Press:  28 December 2020

STÉPHANE CHARPENTIER ,
KARL GROSSE-ERDMANN Open the ORCID record for KARL GROSSE-ERDMANN [Opens in a new window]  and
QUENTIN MENET
STÉPHANE CHARPENTIER
Affiliation:
Institut de Mathématiques de Marseille, UMR 7373, Aix-Marseille Université, 39 rue F. Joliot Curie, 13453 Marseille Cedex 13, France (e-mail: stephane.charpentier.1@univ-amu.fr)
KARL GROSSE-ERDMANN*
Affiliation:
Département de Mathématique, Université de Mons, 20 Place du Parc, 7000Mons, Belgium (e-mail: quentin.menet@umons.ac.be)
QUENTIN MENET
Affiliation:
Département de Mathématique, Université de Mons, 20 Place du Parc, 7000Mons, Belgium (e-mail: quentin.menet@umons.ac.be)
*
e-mail: kg.grosse-erdmann@umons.ac.be
Get access Rights & Permissions [Opens in a new window]

Abstract

Bayart and Ruzsa [Difference sets and frequently hypercyclic weighted shifts. Ergod. Th. & Dynam. Sys.35 (2015), 691–709] have recently shown that every frequently hypercyclic weighted shift on 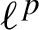$\ell ^p$ is chaotic. This contrasts with an earlier result of Bayart and Grivaux [Frequently hypercyclic operators. Trans. Amer. Math. 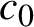Soc.358 (2006), 5083–5117], who constructed a non-chaotic frequently hypercyclic weighted shift on $c_0$ . We first generalize the Bayart–Ruzsa theorem to all Banach sequence spaces in which the unit sequences form a boundedly complete unconditional basis. We then study the relationship between frequent hypercyclicity and chaos for weighted shifts on Fréchet sequence spaces, in particular, on Köthe sequence spaces, and then on the special class of power series spaces. We obtain, rather curiously, that every frequently hypercyclic weighted shift on 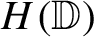$H(\mathbb {D})$ is chaotic, while $H(\mathbb {C})$ admits a non-chaotic frequently hypercyclic weighted shift.

Keywords

chaotic operatorfrequently hypercyclic operatorKöthe sequence spacepower series spaceweighted shift operator

MSC classification

Primary: 47A16: Cyclic vectors, hypercyclic and chaotic operators
Secondary: 47B37: Operators on special spaces (weighted shifts, operators on sequence spaces, etc.) 46A45: Sequence spaces (including Köthe sequence spaces)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 12 , December 2021 , pp. 3634 - 3670
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albanese, A., Bonet, J. and Ricker, W.. The Fréchet spaces $\mathrm{ces}(p+)$ , $1<p<\infty$ . J. Math. Anal. Appl. 458 (2018), 1314–1323.CrossRefGoogle Scholar
Albiac, F. and Kalton, N. J.. Topics in Banach Space Theory. Springer, New York, NY, 2006.Google Scholar
Bayart, F. and Grivaux, S.. Hypercyclicité: le rôle du spectre ponctuel unimodulaire. C. R. Acad. Sci. Paris Ser. I 338 (2004), 703–708.CrossRefGoogle Scholar
Bayart, F. and Grivaux, S.. Frequently hypercyclic operators. Trans. Amer. Math. Soc. 358 (2006), 5083–5117.10.1090/S0002-9947-06-04019-0CrossRefGoogle Scholar
Bayart, F. and Grivaux, S.. Invariant Gaussian measures for operators on Banach spaces and linear dynamics. Proc. Lond. Math. Soc. 94(3) (2007), 181–210.CrossRefGoogle Scholar
Bayart, F. and Matheron, É.. Dynamics of Linear Operators. Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Bayart, F. and Ruzsa, I. Z.. Difference sets and frequently hypercyclic weighted shifts. Ergod. Th. & Dynam. Sys. 35 (2015), 691–709.CrossRefGoogle Scholar
Bierstedt, K. D. and Bonet, J.. Some aspects of the modern theory of Fréchet spaces. RACSAM Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. 97 (2003), 159–188.Google Scholar
Bonet, J.. Topologizable operators on locally convex spaces. Topological Algebras and Applications (Contemporary Mathematics, 427). American Mathematical Society, Providence, RI, 2007, pp. 103–108.10.1090/conm/427/08144CrossRefGoogle Scholar
Bonet, J., Martínez-Giménez, F. and Peris, A.. A Banach space which admits no chaotic operator. Bull. Lond. Math. Soc. 33 (2001), 196–198.CrossRefGoogle Scholar
Bonilla, A. and Grosse-Erdmann, K.-G.. Upper frequent hypercyclicity and related notions. Rev. Mat. Complut. 31 (2018), 673–711.CrossRefGoogle Scholar
Dubinsky, E. and Ramanujan, M. S.. Inclusion theorems for absolutely $\lambda$ -summing maps. Math. Ann. 192 (1971), 177–190.CrossRefGoogle Scholar
Grosse-Erdmann, K.-G.. Hypercyclic and chaotic weighted shifts. Studia Math. 139 (2000), 47–68.CrossRefGoogle Scholar
Grosse-Erdmann, K.-G. and Peris Manguillot, A.. Linear Chaos. Springer, London, 2011.CrossRefGoogle Scholar
Kamthan, P. K. and Gupta, M.. Sequence Spaces and Series. Marcel Dekker, New York, NY, 1981.Google Scholar
Meise, R. and Vogt, D.. Introduction to Functional Analysis. The Clarendon Press, Oxford University Press, New York, NY, 1997.Google Scholar
Menet, Q.. Linear chaos and frequent hypercyclicity. Trans. Amer. Math. Soc. 369 (2017), 4977–4994.CrossRefGoogle Scholar
Shapiro, J. H.. Simple connectivity and linear chaos. Rend. Circ. Mat. Palermo (2) Suppl. no. 56 (1998), 27–48.Google Scholar
Shkarin, S.. On the spectrum of frequently hypercyclic operators. Proc. Amer. Math. Soc. 137 (2009), 123–134.CrossRefGoogle Scholar