Published online by Cambridge University Press: 11 March 2013
Iterated quadratic polynomials give rise to a rich collection of different dynamical systems that are parametrized by a simple complex parameter  $c$. The different dynamical features are encoded by the kneading sequence, which is an infinite sequence over
$c$. The different dynamical features are encoded by the kneading sequence, which is an infinite sequence over 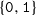 $\{ \mathtt{0} , \mathtt{1} \} $. Not every such sequence actually occurs in complex dynamics. The set of admissible kneading sequences was described by Milnor and Thurston for real quadratic polynomials, and by the authors in the complex case. We prove that the set of admissible kneading sequences has positive Bernoulli measure within the set of sequences over
$\{ \mathtt{0} , \mathtt{1} \} $. Not every such sequence actually occurs in complex dynamics. The set of admissible kneading sequences was described by Milnor and Thurston for real quadratic polynomials, and by the authors in the complex case. We prove that the set of admissible kneading sequences has positive Bernoulli measure within the set of sequences over  $\{ \mathtt{0} , \mathtt{1} \} $.
$\{ \mathtt{0} , \mathtt{1} \} $.