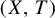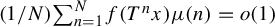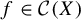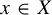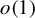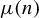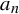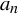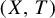1 Introduction
A topological dynamical system is a pair
$(X,T)$
where X is compact metric space and
$T\in \mathcal {C}(X)$
. If the system
$(X,T)$
has zero topological entropy, then Sarnak’s Möbius disjointness conjecture [Reference Sarnak16, Main Conjecture] predicts that
$$ \begin{align} \frac{1}{N}\sum_{n=1} ^{N} \mu(n)f(T^{n} x) = o(1)\quad \text{for every } f\in \mathcal{C}(X) \text{ and every } x\in X. \end{align} $$
Many special cases of Sarnak’s conjecture have been established. A very partial list of examples consists of [Reference Bourgain, Sarnak and Ziegler2, Reference el Abdalaoui, Lemańczyk and de la Rue5, Reference Frantzikinakis and Host8, Reference Green and Tao9]. We refer to the surveys of Ferenczi, Kułaga-Przymus, and Lemańczyk [Reference Ferenczi, Kułaga-Przymus and Lemańczyk6] and of Kułaga-Przymus and Lemańczyk [Reference Kułaga-Przymus and Lemańczyk11] for excellent expositions on the subject, and many more references.
The goal of this paper is to study the rate of decay in Sarnak’s conjecture. That is, to study the nature of the
$o(1)$
as in equation (1). We will show that there are systems for which this
$o(1)$
decays to zero arbitrarily slowly. Nevertheless, all the examples we construct to this end satisfy Sarnak’s conjecture. Here is our main result.
Theorem 1.1. For every decreasing and strictly positive sequence
$\tau (n)\rightarrow 0$
, there is a dynamical system
$(X,T)$
with zero topological entropy that satisfies the following.
-
(1) There exist
$x\in X$
and
$f\in \mathcal {C}(X)$
such that:
$$ \begin{align*}\limsup_{N\rightarrow \infty} \frac{ ({1}/{N})\! \sum_{n=1}^{N} f(T^{n} x)\mu(n) }{\tau(n)}>0.\end{align*} $$
-
(2) The system
$(X,T)$
satisfies Sarnak’s conjecture in equation (1).
Several remarks are in order. First, Sarnak [Reference Sarnak15, the remark following Main Conjecture] remarks that rates are not required in the conjecture, and this is formally justified by Theorem 1.1. Second, it is natural to ask if Theorem 1.1 may be upgraded by finding a zero entropy dynamical system
$(X,T)$
and
$f\in \mathcal {C}(X)$
such that for every rate function
$\tau $
, we can find
$x\in X$
that satisfies Theorem 1.1(1). Doing so is as hard as solving the full Möbius disjointness conjecture. Indeed, by [Reference el Abdalaoui, Kułaga-Przymus, Lemańczyk and de la Rue4, Corollary 10], if the conjecture is true, then for every zero entropy system
$(X,T)$
and
$f\in \mathcal {C}(X)$
, equation (1) holds uniformly in
$x\in X$
. This cannot hold concurrently with the aforementioned upgraded version of Theorem 1.1. In other words, Theorem 1.1 is conjecturally optimal. Next, we remark that in many cases (possibly in all cases), it is known [Reference Tao17] that a sufficiently fast rate in Sarnak’s conjecture implies that the system
$(X,T)$
satisfies a prime number theorem (PNT) in the sense discussed in [Reference Ferenczi, Kułaga-Przymus and Lemańczyk6, Section 11.2]. Thus, recent examples [Reference Frączek, Kanigowski and Lemańczyk7, Reference Kanigowski, Lemańczyk and Radziwiłł10] of zero entropy systems failing to satisfy a PNT can be viewed as evidence toward Theorem 1.1. We also mention the recent interesting counterexamples to polynomial Sarnak’s conjecture constructed by Lian and Shi [Reference Lian and Shi12] and Kanigowski, Lemańczyk, and Radziwiłł [Reference Kanigowski, Lemańczyk and Radziwiłł10] that, while not directly related to Theorem 1.1 as they focus on a sparse sequence of observations instead of the entire trajectory, are similar in spirit to our work.
Finally, we remark that our construction was partially inspired by the idea of building a sufficiently complex zero entropy system as a skew product from the recent work of Dolgopyat et al [Reference Dolgopyat, Dong, Kanigowski and Nándori3], where they exhibit some new classes of zero entropy smooth systems that satisfy the central limit theorem. In this paper, we construct a symbolic skew product instead of a smooth one to code more precise information carried by
$\{a_{n}\}$
.
We will derive Theorem 1.1 from a more general statement. This is the following theorem, which forms the main technical result of this paper.
Theorem 1.2. For every decreasing and strictly positive sequence
$\tau (n)\rightarrow 0$
, there is a zero entropy dynamical system
$(X,T)$
and some
$f\in \mathcal {C}(X)$
that satisfy the following.
-
(1) Every sequence
$|a_{n}|\leq 1$
with
$\limsup _{N\rightarrow \infty } ({1}/{N})\!\sum _{n=1}^{N}\! |a_{n}|>0$
admits some
$x\in X$
such that
$$ \begin{align*}\limsup_{N \rightarrow \infty} \frac{ ({1}/{N})\! \sum_{n=1} ^{N}\! f(T^{n} x)a_{n} }{\tau(n)}>0.\end{align*} $$
-
(2) The system
$(X,T)$
satisfies Sarnak’s conjecture in equation (1).
In fact, we will show that any subsequence
$N_{j}$
such that
$$ \begin{align} \lim_{j\rightarrow \infty} \frac{1}{N_{j}}\sum_{n=1} ^{N_{j}} |a_{n}| =\theta>0 \end{align} $$
admits a further subsequence
$N_{j_{k}}$
such that for all k large enough,
$$ \begin{align*}\frac{1}{N_{j_{k}}} \sum_{n=1} ^{N_{j_{k}}} f(T^{n} x) a_{n} \geq \theta \cdot \tau(N_{j_{k}}).\end{align*} $$
We emphasize that in Theorem 1.2, the system
$(X,T)$
and the function
$f\in \mathcal {C}(X)$
only depend on the rate function
$\tau $
, while the point
$x\in X$
depends also on the sequence
$a_{n}$
. (Indeed,
$(X,T)$
is always a subsystem of the same ambient system, which is the product of four skew product systems with Bernoulli fiber and Bernoulli base and an addition finite system. When regarded as a function on this ambient system, f is also independent of
$\tau $
.)
The derivation of Theorem 1.1 from Theorem 1.2 is straightforward. It is well known that the Möbius function
$\mu $
satisfies
$$ \begin{align*} \lim_{N\rightarrow \infty} \frac{\sum_{n=1} ^{N} |\mu(n)|}{N} = \frac{6}{\pi^{2}}>0,\end{align*} $$
see e.g. [Reference Bateman and Diamond1, Corollary 1.6]. Thus, Theorem 1.2 applied with
$a_{n} = \mu (n)$
gives Theorem 1.1.
We end this introduction with a brief explanation of our construction. We consider subshifts of
$(\lbrace -1,0,1 \rbrace ^{\mathbb {N}} \times \lbrace \lbrace -1,0,1 \rbrace ^{\mathbb {Z}}, T)$
, where
$T(y,z)=(\sigma y, \sigma ^{y_{1}} z)$
and
$\sigma $
is the left shift. Given a rate function
$\tau $
, we first construct a certain rapidly growing sequence
$q_{k}\rightarrow \infty $
. We then construct a subshift such that its base comes from words of length
$q_{k+1}-q_{k}$
that have non-zero entries at distance at least
$q_{k}$
from each other. Our space X is a product of four spaces constructed this way, together with a finite set
$\lbrace 0,1,2,3 \rbrace $
. The function f is taken to be
$$ \begin{align*}f( (y^{(0)}, z^{(0)}), (y^{(1)}, z^{(1)}), (y^{(2)}, z^{(2)}), (y^{(3)}, z^{(3)}), i) = z_{0} ^{(i)}.\end{align*} $$
We need four spaces in this construction for the reasons below. To retrieve positive correlation between observation
$f(T^{n}x)$
and
$a_{n}$
from positive correlation between
$a(n)$
and the sequence
$\gamma _{n}=\operatorname *{\mathrm {sign}} a(n)$
, we make
$\{f(T^{q_{k}j+b}x)\}$
mimic
$\{\gamma _{q_{k}j+c}\}$
for
$n=q_{k}j+b\in [q_{k},{q_{k+1}}/3]$
. For this analysis to be applied to most steps in the trajectory, we shall use two different sequences
$\{q_{k}^{(0)}\}$
,
$q_{k}^{(1)}$
such that the intervals
$[q_{k}^{(1)}, {q_{k+1}^{(1)}}/3]$
and
$[q_{k}^{(0)}, {q_{k+1}^{(0)}}/3]$
together cover
$\mathbb N$
. In addition, to express the average of
$f(T^{n}x)a_{n}$
as an approximate linear combination of that of
$\gamma _{q_{k}j+c}a_{n}=\gamma _{q_{k}j+c}a_{q_{k}j+b}$
, one has to explore different pairs of congruences
$(b,c)$
and use two different values q and
$q-1$
for q, as explained in the paragraph below. Thus, two more different sequences
$\{q_{k}^{(2)}=q_{k}^{(0)}-1\}$
and
$\{q_{k}^{(3)}=q_{k}^{(1)}-1\}$
are needed. Each of the four sequences
$\{q_{k}^{(i)}\}$
corresponds to a different space
$X^{(i)}$
. We remark that if
$\lim _{N\rightarrow \infty } ({1}/{N})\!\sum _{n=1}^{N} |a_{n}|>0$
is assumed instead of
$\limsup _{N\rightarrow \infty } ({1}/{N})\!\sum _{n=1}^{N} |a_{n}|>0$
, then only two spaces will be needed as the first concern above is no longer an issue in this case.
Given
$a_{n}$
as in Theorem 1.2(1), our construction of the point
$x\in X$
relies on the following observation. Assuming
$a_{n} \in \mathbb {R}$
(otherwise one can pass to either
$\textrm{Re} (a_{n})$
or
$\textrm{Im} (a_{n})$
), let
$\gamma _{n} := \text {sign}(a_{n})$
, and let
$N_{j}$
,
$\theta $
be as in equation (2). For every
$q,M \gg 1$
, one may show that
$$ \begin{align*}\max_{ c,d\in [0,q]\cap \mathbb{Z}} \bigg\lbrace \frac{1}{qM} \sum_{b=c}^{q-1+c} \sum_{n=1}^{M} \gamma {}_{qn+c} \cdot a_{qn+b},\, \frac{-1}{qM} \sum_{b=d}^{q-1+d} \sum_{n=1}^{M} \gamma {}_{qn+d+1} \cdot a_{qn+b} \bigg \rbrace \geq \frac{\theta}{4}.\end{align*} $$
Here we pick
$k=k(j)$
in some convenient way,
$q=q_{k}$
, and
$M\approx {N_{j}}/{q_{k}}$
. We then construct our point x via working in one of the subshifts in our space—the exact choice depends on certain technical issues coming from the relation between
$N_{j}$
and
$q_{k}$
. To set up x, we carefully concatenate pieces of arithmetic progressions in
$\gamma $
or
$-\gamma $
in the fiber (using the equation above), with the base living in the corresponding shift space and behaving nicely along the observable f. This will allow us to find a subsequence of
$N_{j}$
where the linear correlations as in Theorem 1.2(1) are well approximated by the average giving the
$\max $
in the equation above. Thus, with some more work, we bound these correlations from below by
$\tau (N_{j})\cdot \theta $
.
Finally, to derive Theorem 1.2(2), we apply the Matomäki–Radziwiłł bound [Reference Matomäki and Radziwiłł13] on averages of multiplicative functions along short intervals. To do this, we exploit some strong periodic behavior that exists in the systems we construct.
2 Proof of Theorem 1.2(1).
2.1 Preliminaries
Let
$(X,T)$
be a dynamical system, where we recall that X is a compact metric space and
$T\in \mathcal {C}(X)$
. We denote the metric on X by
$d_{X}$
. Let us recall the Bowen–Dinaburg definition of topological entropy (as in e.g. [Reference Walters18]). For every
$n\in \mathbb {N}$
, we define a metric on X via
$$ \begin{align*}d_{n}(x,y) = \max \lbrace d_{X} (T^{i} (x), T^{i}(y)): 0\leq i <n \rbrace.\end{align*} $$
A Bowen ball
$B_{n} (x,\epsilon )$
of depth n centered at
$x\in X$
of radius
$\epsilon>0$
is the corresponding (open) ball in the metric
$d_{n}$
,
$$ \begin{align*}B_{n} (x,\epsilon) = \lbrace y\in X: d_{n}(x,y)<\epsilon\rbrace.\end{align*} $$
For any set
$E\subseteq X$
, let
$N(E,n,\epsilon )$
denote the minimal number of Bowen balls of depth n and radius
$\epsilon $
needed to cover E. The topological entropy of
$(X,T)$
is then defined as
$$ \begin{align*}h(T):= \lim_{\epsilon \rightarrow 0} \bigg( \limsup_{n\rightarrow \infty} \frac{\log N(X, n,\epsilon)}{n} \bigg).\end{align*} $$
Next, let
$\sigma : \lbrace -1, 0 ,1\rbrace ^{\mathbb {Z}} \rightarrow \lbrace -1, 0 ,1\rbrace ^{\mathbb {Z}}$
denote the left shift. On
$\lbrace -1, 0 ,1\rbrace ^{\mathbb {Z}}$
and
$\lbrace -1, 0 ,1\rbrace ^{\mathbb {N}}$
, we define the metric
$$ \begin{align*} d(x,y) = 3^{- \min \lbrace |n|: x_{n} \neq y_{n} \rbrace}.\end{align*} $$
Also, for every
$x\in \lbrace -1, 0 ,1\rbrace ^{\mathbb {N}}$
and
$k>l\in \mathbb {N}$
, let
$x|_{l}^{k} \in \lbrace -1,0,1\rbrace ^{k-l}$
be the word
$$ \begin{align*}x|_{l} ^{k} := (x_{l},x_{l+1},\ldots,x_{k}),\end{align*} $$
and we use similar notation in the space
$\lbrace -1, 0 ,1\rbrace ^{\mathbb {Z}}$
as well. Next, let
$$ \begin{align*}Z:=\lbrace-1, 0 ,1\rbrace^{\mathbb{N}} \times \lbrace-1, 0 ,1\rbrace^{\mathbb{Z}}\end{align*} $$
and endow Z with the sup-metric on both its coordinates. Note that open balls in this metric are also closed, and thus for every
$n\in \mathbb {N}$
,
$x\in X$
, and
$\epsilon>0$
, the Bowen ball
$B_{n} (x,\epsilon )$
is closed. Also, we denote by
$\Pi _{i}$
,
$i=1,2$
, the coordinate projections in Z. Finally, we define the skew-product
$T:Z\rightarrow Z$
via
$$ \begin{align*}T(y,z) = (\sigma(y), \sigma^{y_{1}} (z)).\end{align*} $$
We say that
$X\subseteq Z$
is a subshift if it is closed and T-invariant.
We will require the following lemma.
Lemma 2.1. The system
$(Z,T)$
satisfies that for every
$n\in \mathbb {N}$
,
$\epsilon>0$
, and
$x=(y,z)\in Z$
, the following hold.
-
(1) We have
$$ \begin{align*}T^{n} (y, z) = ( \sigma^{n} y, \sigma^{\sum_{i=1} ^{n} y_{i}} z ).\end{align*} $$
-
(2) Let
$m\kern1.2pt{=}\kern1.2pt m(n,y) \kern1.2pt{=}\kern1.2pt \min \lbrace \min _{1\leq k\leq n} \sum _{i=1}^{k} y_{i}, 0 \rbrace $
and
$M \kern1.2pt{:=}\kern1.2pt M(n,y)\kern1.2pt{=}\kern1.2pt \max \lbrace \max _{1\leq k\leq n} \sum _{i=1}^{k} y_{i}, 0 \rbrace $
. Then for any
$l\in \mathbb {N}$
, the Bowen ball
$d_{n}(x, 3^{-l})$
equals
$$ \begin{align*} \lbrace (a,b)\in Z: a|_{1} ^{n+u} = y|_{1} ^{n+u}, b|_{m-u} ^{M+u} = z|_{m-u} ^{M+u} \rbrace.\end{align*} $$
-
(3) For any set
$E\subseteq Z$
, where
$$ \begin{align*}N(E, n ,\epsilon) = N(\mathrm{cl}(E), n ,\epsilon),\end{align*} $$
$\mathrm{cl}(E)$
is the closure of the set E.
Proof. Part (1) follows immediately from the definition of the map T. Part (2) follows from part (1). Finally, part (3) is an immediate consequence of the fact that in
$(Z, T)$
, Bowen balls are closed.
2.2 Construction of some zero entropy systems
Fix a sequence
$\tau (n) \rightarrow 0$
as in Theorem 1.2. We begin by constructing a rapidly growing sequence
$q_{k} \rightarrow \infty $
(that depends on
$\tau $
) such that for every
$k\in \mathbb {N}$
, we have the following.
-
(1)
$q_{k+1}> q_{k}^{4} + 3q_{k}$
. -
(2)
$\tau ( {q_{k+1}}/{3}) < {1}/{16q_{k}}$
.
We now use
$q_{k}$
to define four sequences:
$$ \begin{align*}q_{k} ^{(0)}:=q_{2k},\quad q_{k} ^{(1)}=q_{2k+1},\quad q_{k} ^{(2)} := q_{k} ^{(0)} -1,\quad q_{k} ^{(3)} := q_{k} ^{(1)} -1.\end{align*} $$
Notice that property (1) above also holds for
$q_{k}^{(i)}$
for every
$i\in \lbrace 0,1,2,3\rbrace $
. In particular,
$$ \begin{align*}\lim_{k\rightarrow \infty} \frac{q_{k+1} ^{(i)} }{q_{k} ^{(i)}} = \infty \quad\text{for every } i\in \lbrace 0,1,2,3\rbrace.\end{align*} $$
Next, for every
$i\in \lbrace 0,1,2, 3\rbrace $
and every k, let
$$ \begin{align*}A_{k} ^{(i)} := \lbrace j\cdot q_{k} ^{(i)}: j\in \mathbb{Z}, q_{k} ^{(i)} \leq j\cdot q_{k} ^{(i)} \leq q_{k+1} ^{(i)} \rbrace.\end{align*} $$
For every
$i\in \lbrace 0,1,2,3 \rbrace $
and every
$k\in \mathbb {N}$
, we construct elements
$s^{(i)}_{k} \in \lbrace -1,0,1\rbrace ^{\mathbb {N}}$
such that the following hold.
-
(1)
$ s^{(i)}_{k} (n) = 0$
for every integer
$n\notin A_{k}^{(i)} $
. -
(2) For every
$j\cdot q_{k}^{(i)} \in A_{k}^{(i)}$
, and
$$ \begin{align*} s^{(i)} _{k} (j\cdot q_{k} ^{(i)})=1 \quad\text{if } j \leq \bigg[\frac{q_{k+1} ^{(i)} }{3 q_{k} ^{(i)}}\bigg],\end{align*} $$
$$ \begin{align*}s^{(i)} _{k} (j\cdot q_{k} ^{(i)} )=-1 \quad\text{if } \bigg[\frac{q_{k+1} ^{(i)} }{3 q_{k} ^{(i)}}\bigg] < j\leq 2\bigg[\frac{q_{k+1} ^{(i)} }{3 q_{k} ^{(i)}}\bigg].\end{align*} $$
Next, for every element
$x\in \lbrace -1,0,1\rbrace ^{\mathbb {N}}$
and
$p\in \mathbb {N}_{0}$
, we define
$\sigma ^{-p} x\in \lbrace -1,0,1\rbrace ^{\mathbb {N}}$
as
$\sigma ^{-p} x = x$
if
$p=0$
, and otherwise
$$ \begin{align*}( \sigma^{-p} x )|_{1} ^{p} = (0,\ldots,0) \quad\text{and for all } n>p, \sigma^{-p} x (n) = x(n-p).\end{align*} $$
The following lemma is an immediate consequence of our construction.
Lemma 2.2. For every
$i\in \lbrace 0,1,2, 3\rbrace $
,
$k\in \mathbb {N}$
, and
$p = 0,\ldots ,q_{k}^{(i)}$
, we have
$$ \begin{align*}\sum_{n \in [q_{k} ^{(i)}, \, q_{k+1} ^{(i)}) \cap \mathbb{Z} } ( \sigma^{-p} s^{(i)} _{k} ) (n ) =0.\end{align*} $$
Proof. This follows since by our construction,
$$ \begin{align*} | \lbrace j\cdot q_{k} ^{(i)} \in A_{k} ^{(i)}: s^{(i)} _{k} (j\cdot q_{k} ^{(i)})=1 \rbrace | = | \lbrace j\cdot q_{k} ^{(i)} \in A_{k} ^{(i)}: s^{(i)} _{k} (j\cdot q_{k} ^{(i)})=-1 \rbrace |,\end{align*} $$
as well as the fact that for all
$n\in A_{k}^{(i)}$
and
$p = 0,\ldots ,q_{k}^{(i)}$
,
$n+p$
is still in the interval
$[q_{k}^{(i)}, \, q_{k+1}^{(i)}) \cap \mathbb {Z} $
.
Next, for every
$i \in \lbrace 0,1,2,3 \rbrace $
and
$k \in \mathbb {N}$
, define the truncations
$$ \begin{align*}R^{(i)} _{k} = \lbrace ( \sigma^{-p} s^{(i)} _{k} )|_{ q_{k} ^{(i)} } ^{ q_{k+1}^{(i)}-1} : p = 0,\ldots,q_{k} ^{(i)} \rbrace \subseteq \lbrace -1,0,1\rbrace^{ q_{k+1} ^{(i)} - q_{k} ^{(i)}}.\end{align*} $$
We now define the space
$P^{(i)}$
of all infinite sequences that have, for every k, some word from
$R^{(i)}_{k}$
between their
$q_{k}^{(i)}$
and
$q_{k+1}^{(i)}-1$
digits. Formally,
$$ \begin{align*}P^{(i)} = \lbrace x\in \lbrace -1, 0, 1 \rbrace^{\mathbb{N}}: x|_{ q_{k} ^{(i)} } ^{ q_{k+1}^{(i)}-1} \in R^{(i)} _{k} \text{ and } x|_{1} ^{q_{1}^{(i)} -1} =(0,\ldots,0) \rbrace. \end{align*} $$
The following lemma is an immediate consequence of Lemma 2.2.
Lemma 2.3. For every
$i\in \lbrace 0,1,2,3\rbrace $
,
$k\in \mathbb {N}$
, and
$y\in P^{(i)}$
,
$$ \begin{align*}\sum_{j=1} ^{q_{k}^{(i)} -1} y(j) = 0.\end{align*} $$
Finally, for every
$i\in \lbrace 0 ,1,2,3 \rbrace $
, we define the subshift of
$(Z,T)$
,
$$ \begin{align*}X_{i} = \text{cl} \bigg( \bigcup_{n\in \mathbb{N}_{0}} T^{n} ( P^{(i)} \times \lbrace -1,0,1\rbrace^{\mathbb{Z}} ) \bigg) .\end{align*} $$
Lemma 2.4. For every
$i\in \lbrace 0,1,2,3\rbrace $
, we have
$h(X_{i}, T)=0$
.
Proof. Fix
$n,u\in \mathbb {N}$
. We count how many Bowen balls of radius
${1}/{3^{u}}$
and depth n are needed to cover
$X_{i}$
. Recall that we denote this quantity by
$N(X_{i}, n,{1}/{3^{u}})$
. By Lemma 2.1(3), this is the same number as
$$ \begin{align*}N \bigg( \bigcup_{l\in \mathbb{N}_{0}} T^{l} ( P^{(i)} \times \lbrace -1,0,1\rbrace^{\mathbb{Z}} ) , n, \frac{1}{3^{u}} \bigg).\end{align*} $$
So, we work with the latter space (that is, without taking the closure).
Let
$k=k(n+u,i)$
be such that
$$ \begin{align} q_{k} ^{(i)} \leq n+u < q_{k+1} ^{(i)}. \end{align} $$
Our first observation is that we can write
$$ \begin{align*} \bigcup_{l\in \mathbb{N}_{0}} T^{l} ( P^{(i)} \times \lbrace -1,0,1\rbrace^{\mathbb{Z}} ) = A_{1} \bigcup A_{2} \bigcup A_{3}.\end{align*} $$
To define the sets
$A_{i}$
, we first note that every
$x\in \bigcup _{l\in \mathbb {N}_{0}} T^{l} ( P^{(i)} \times \lbrace -1,0,1\rbrace ^{\mathbb {Z}} )$
admits some
$l\in \mathbb {N}_{0}$
and
$\tilde {x} \in P^{(i)} \times \lbrace -1,0,1\rbrace ^{\mathbb {Z}}$
such that
$x = T^{l} \tilde {x}$
. We denote by
$p=p(x)\in \mathbb {N}$
the unique integer such that
$q_{k-1}^{(i)} +l \in [q_{p}^{(i)},\, q_{p+1}^{(i)})$
. Note that
$p\geq k-1$
. Then,
$$ \begin{align*}A_{1} = \lbrace x: p(x)\geq k+1\rbrace, \quad A_{2} = \lbrace x: p(x)= k\rbrace, \quad A_{3} = \lbrace x: p(x)= k-1\rbrace.\end{align*} $$
Thus, we bound the covering numbers for
$A_{1}$
,
$A_{2}$
,
$A_{3}$
separately. Before doing so, we notice that for any
$x\in A_{j}$
for
$j=1,2,3$
, there are at most
$3^{ q_{k-1}^{(i)}}$
possibilities for the first
$q_{k-1}^{(i)}$
digits of
$\Pi _{1} (x)$
(see Figure 1).
Figure 1 Illustration for Lemma 2.4.
(i) Covering
$A_{1}$
. For any
$x\in A_{1}$
, the word
$( \Pi _{1} x ) |_{ q_{k-1}^{(i)}}^{n+u}$
always consists of zeros separated by
$1$
or
$-1$
, and in this case, the non-zero entries appear at a distance at least
$q_{k+1}^{(i)}>n+u$
from each other. Since there can be only one non-zero entry, there are at most
$2(n+u)$
options for the configuration of this word. So, with the notation of Lemma 2.1(2), we see that
$$ \begin{align*}|m|,M \leq q_{k-1} ^{(i)}+1.\end{align*} $$
Thus, taking into account also the first
$q_{k-1}^{(i)}$
digits, and via Lemma 2.1(2), the number of Bowen balls we need here is at most
$$ \begin{align*}( 3^{ q_{k-1} ^{(i)}} \times 2(n+u) ) \times ( 3^{u+q_{k-1} ^{(i)}+1} )^{2}.\end{align*} $$
(ii) Covering
$A_{2}$
. The word
$( \Pi _{1} x ) |_{ q_{k-1}^{(i)}}^{n+u}$
consists of zeros separated by
$1$
or
$-1$
, and in this case, the first non-zero entries appear at a distance at least
$q_{k}^{(i)} \leq n+u$
from each other. We also know that the first non-zero digit needs to appear within the first
$q_{k}^{(i)}$
digits. Another factor that needs to be taken into consideration is the possibility that
$[q_{k-1}^{(i)}+l, n+u+l]$
intersects
$[q_{k+1}^{(i)}, \infty )$
. So, with the notation of Lemma 2.1(2), we see that
$$ \begin{align*}|m|,M \leq q_{k-1} ^{(i)}+\frac{ n+u }{ q_{k} ^{(i)} }+1.\end{align*} $$
Taking all these factor into account, the number of Bowen balls we need here is at most
$$ \begin{align*} ( 3^{ q_{k-1} ^{(i)}}\times q_{k} ^{(i)} \times 2(n+u) ) \times ( 3^{u+ q_{k-1} ^{(i)} + { (n+u) }/{ q_{k} ^{(i)} }+1} )^{2}.\end{align*} $$
(iii) Covering
$A_{3}$
. The word
$( \Pi _{1} x ) |_{ q_{k-1}^{(i)}}^{n+u}$
consists of zeros separated by
$1$
or
$-1$
, and in this case, the first non-zero entries appear at a distance at least
$q_{k-1}^{(i)}$
from each other. We also know that the first non-zero digit needs to appear within the first
$q_{k-1}^{(i)}$
digits. Another factor that needs to be taken into consideration is the possibility that
$[q_{k-1}^{(i)}+l, n+u+l]$
intersects
$[q_{k}^{(i)}, \infty )$
. So, with the notation of Lemma 2.1(2), we see that
$$ \begin{align*}|m|,M \leq q_{k-1} ^{(i)}+\frac{q_{k} ^{(i)} }{ q_{k-1} ^{(i)} }+ \frac{ n+u }{ q_{k} ^{(i)} } +1.\end{align*} $$
Taking all these factors into account, the number of Bowen balls we need here is at most
$$ \begin{align*}( 3^{ q_{k-1} ^{(i)}} \times q_{k-1} ^{(i)} \times q_{k} ^{(i)} \times 2(n+u) ) \times ( 3^{u+ q_{k-1} ^{(i)}+{q_{k} ^{(i)} }/{ q_{k-1} ^{(i)} }+ { (n+u) }/{ q_{k} ^{(i)} }+1} )^{2} .\end{align*} $$
Thus, we see that
$$ \begin{align*} N\bigg(X_{i}, n,\frac{1}{3^{u}}\bigg) \leq 3\cdot \max_{i=1,2,3} N\bigg(A_{i},n,\frac{1}{3^{u}}\bigg) = 3\cdot N\bigg(A_{3},n,\frac{1}{3^{u}}\bigg),\end{align*} $$
which has been computed in point (iii) above. So, making use of equation (3),
$$ \begin{align*} &\frac{\log N(X_{i}, n, {1}/{3^{u}} )}{n}\\&\quad\leq \frac{\log 3 + \log ( 3^{ q_{k-1} ^{(i)}} \cdot 2(n+u) \cdot q_{k-1} ^{(i)} \cdot q_{k} ^{(i)} ) \cdot ( 3^{u+ q_{k-1} ^{(i)}+{q_{k} ^{(i)} }/{ q_{k-1} ^{(i)} }+ { (n+u) }/{ q_{k} ^{(i)} }+1} )^{2} }{n} \\&\quad\leq \frac{\log 6}{n} + \frac{q_{k-1} ^{(i)}\cdot \log 3}{n} + \frac{\log (n+u)}{n} + \frac{2\log q_{k} ^{(i)}}{n} \\& \qquad + \frac{\bigg(u+q_{k-1} ^{(i)}+{q_{k} ^{(i)} }/{ q_{k-1} ^{(i)} }+ { n+u}/{ q_{k} ^{(i)} } +1 \bigg) \log 9 }{n} \\&\quad\leq C_{1} \cdot \bigg( \frac{ \log q_{k} ^{(i)}}{n} + \frac{q_{k-1} ^{(i)}}{n}+\frac{\log (n+u)}{n}+ \frac{q_{k} ^{(i)} }{ q_{k-1} ^{(i)} \cdot (n+u)}\cdot \frac{n+u}{n} + \frac{ n+u }{ q_{k} ^{(i)} \cdot n } \bigg) \\&\quad\leq C_{1} \cdot \frac{n+u}{n} \cdot \bigg( \frac{ 2\log (n+u)}{n} + \frac{q_{k-1} ^{(i)}}{q_{k} ^{(i)}}+ \frac{1 }{ q_{k-1} ^{(i)} } + \frac{1 }{ q_{k} ^{(i)} } \bigg). \end{align*} $$
Here,
$C_{1}$
is a large constant that depends variously on u and the other constants appearing in the second equation. We conclude that, fixing u,
$$ \begin{align*} \lim_{n\rightarrow \infty} \frac{\log N(X, n, {1}/{3^{u}} )}{n} =0, \end{align*} $$
and the claim is proved.
2.3 Finding correlations along arithmetic progressions
Let
$a_{n}$
be a sequence as in Theorem 1.2(1), that is, such that
$\limsup _{N\rightarrow \infty } ({1}/{N})\!\sum _{n=1}^{N}\! |a_{n}|>0$
. By moving to either
$\textrm{Re} (a_{n})$
or
$\textrm{Im} (a_{n})$
, we may assume
$a_{n}$
is a real valued sequence. We define a new sequence
$\gamma _{n} \in \lbrace -1, 0, 1\rbrace $
via
$$ \begin{align*}\gamma_{n} :=\operatorname*{\mathrm{sign}}(a_{n}).\end{align*} $$
In particular,
$$ \begin{align*}\limsup_{N\rightarrow \infty} \frac{1}{N}\sum_{n=1} ^{N} \gamma_{n} \cdot a_{n} = \limsup_{N\rightarrow \infty} \frac{1}{N}\sum_{n=1} ^{N} |a_{n}|>0.\end{align*} $$
Let
$\theta := \limsup ({1}/{N})\!\sum _{n=1}^{N}\! |a_{n}|>0$
, and let
$N_{j}$
be a subsequence such that
$$ \begin{align*}\lim_{j\rightarrow \infty} \frac{1}{N_{j}}\sum_{n=1} ^{N_{j}} |a_{n}|= \theta.\end{align*} $$
Definition 2.5. For every
$j\in \mathbb {N}$
large enough, we define
$k^{\prime }=k(j)\in \mathbb {N}$
and
$i^{\prime }=i(j)\in \lbrace 0, 1\rbrace $
as the unique integers such that:
$$ \begin{align*}\text{if } N_{j} \in \bigg[\frac{q_{k^{\prime}} ^{(1)}}{3},\, \frac{q_{k^{\prime}+1}^{(0)}}{3}\bigg) \quad\text{then } i^{\prime} =0; \text{ and }\end{align*} $$
$$ \begin{align*}\text{if } N_{j} \in \bigg[\frac{q_{k^{\prime}+1} ^{(0)}}{3},\, \frac{q_{k^{\prime}+1}^{(1)}}{3}\bigg) \quad\text{then } i^{\prime} =1.\end{align*} $$
We also define an integer
$$ \begin{align*}M_{k^{\prime}} ^{(i^{\prime})} := \bigg[\frac{N_{j}}{q_{k^{\prime}}^{(i^{\prime})}}\bigg].\end{align*} $$
Note that by definition and the construction of the sequence
$q_{k}$
,
$$ \begin{align} \frac{( q_{k^{\prime}} ^{(i^{\prime})} )^{3}}{3}=\frac{( q_{k^{\prime}} ^{(i^{\prime})} )^{4}}{3q_{k^{\prime}} ^{(i^{\prime})}} < M_{k^{\prime}} ^{(i^{\prime})} \leq \frac{q_{k^{\prime}+1} ^{(i^{\prime})}}{3q_{k^{\prime}} ^{(i^{\prime})}}. \end{align} $$
Next, recall the definition of Z from §2.1 and let
$g:Z\rightarrow \lbrace -1,0,1\rbrace $
be the function
$$ \begin{align*}g(y,z) = z_{0}.\end{align*} $$
For every
$q,M \gg 1$
and
$r,c$
such that
$r,c\in [0,q]$
, let
$$ \begin{align*}A_{r,c} ^{q ,M}:= \frac{1}{qM} \sum_{b=r} ^{q-1+r} \sum_{n=1} ^{M} \gamma (qn+c) \cdot a(qn+b).\end{align*} $$
Finally, we also define
$$ \begin{align*}M_{k^{\prime}} ^{(i^{\prime}+2)} := \bigg[ \frac{q_{k^{\prime}} ^{(i^{\prime})} M_{k^{\prime}} ^{(i^{\prime})} }{q_{k^{\prime}} ^{(i^{\prime})}-1} \bigg] = \bigg[ \frac{q_{k^{\prime}} ^{(i^{\prime})} M_{k^{\prime}} ^{(i^{\prime})}}{q_{k^{\prime}} ^{(i^{\prime}+2)}} \bigg]\end{align*} $$
and note that
$M_{k^{\prime }}^{(i^{\prime }+2)} \approx M_{k^{\prime }}^{(i^{\prime })} $
. In the following lemma, we use the construction from §2.2.
Lemma 2.6. For every j and
$u\in \lbrace 0,1\rbrace $
writing
$\ell = i^{\prime }+2u$
, for every two integers
$c,r \in [0, q_{k^{\prime }}^{(\ell )}]$
, let
$x \in P^{(\ell )} \times \lbrace -1,0,1\rbrace ^{\mathbb {Z}} \subseteq X_{\ell }$
be any element such that for every
$ q_{k^{\prime }}^{(\ell )} \leq n< q_{k^{\prime }+1}^{(\ell )}$
,
$$ \begin{align*}x (n) = ( s_{k^{\prime}} ^{(\ell)}(n-r), \gamma( q_{k^{\prime}} ^{(\ell)} \cdot n+c) ).\end{align*} $$
Then
$$ \begin{align*}\frac{1}{q_{k^{\prime}} ^{(\ell)}M_{k^{\prime}} ^{(\ell)} } \sum_{n=1} ^{q_{k^{\prime}}^{(\ell)}M_{k^{\prime}}^{(\ell)}} g(T^{n} x ) a(n) = A_{r,c} ^{q_{k^{\prime}}^{(\ell)}, \, M_{k^{\prime}}^{(\ell)} } + O\bigg( \frac{ q_{k^{\prime}} ^{(\ell)} }{M_{k^{\prime}} ^{(\ell)}} \bigg).\end{align*} $$
Note that by the construction of
$P^{(\ell )} \times \lbrace -1,0,1\rbrace ^{\mathbb {Z}}$
in §2.2, there exists an element x as in the statement of the lemma in that space.
Proof. In this proof, we suppress the
$\ell ,k^{\prime }$
in our notation and simply write
$q, M.$
First, for every two integers
$j\in [1, M]$
and
$b\in [r, q+r-1]$
,
$$ \begin{align*} \sum_{d=1} ^{qj+b} ( \Pi_{1} x ) (d) &= \sum_{d=1} ^{q-1} ( \Pi_{1} x ) (d)+ \sum_{d=q} ^{qj+b-1} ( \Pi_{1} x ) (d)\\ &= \sum_{d=q} ^{qj+b-1} s_{k} ^{(\ell)} (d-r)\\ &= \sum_{d=q-r} ^{qj+b-r-1} s_{k} ^{(\ell)} (d) = j. \end{align*} $$
Note the use of Lemma 2.3 in the second equality. Moreover, in the last equality, we use the fact that
$M\leq {q_{k^{\prime }+1}^{(\ell )} }/{3 q_{k^{\prime }}^{(\ell )}}$
and the definition of
$s_{k}^{(\ell )}$
to guarantee that all summands are either
$0$
or
$1$
. Therefore,
$$ \begin{align*} \frac{1}{q M } \sum_{n=1} ^{q M} g(T^{n} x) a(n) &= \frac{1}{q M } \sum_{n=q} ^{q M} g(T^{n} x) a(n) + O\bigg( \frac{1}{M } \bigg) \\[3pt]&= \frac{1}{q M } \sum_{j=1} ^{M} \sum_{b=r} ^{q+r -1} g(T^{q\cdot j+b} x) a(q\cdot j+b) + O\bigg( \frac{1}{ M } \bigg) \\[3pt]&= \frac{1}{q M } \sum_{j=1} ^{M} \sum_{b=r} ^{q+r -1} g( \sigma^{qj+b} \Pi_{1} x, \sigma^{ \sum_{d=1} ^{qj+b} ( \Pi_{1} x ) (d)} \Pi_{2} x ) a(q\cdot j+b) \\[3pt]& \quad +\, O\bigg( \frac{1}{ M } \bigg)\\[3pt]&= \frac{1}{q M } \sum_{j=1} ^{M} \sum_{b=r} ^{q+r -1} g( \sigma^{qj+b-r} s_{k^{\prime}} ^{(\ell)}, \sigma^{j} \Pi_{2} x ) a(q\cdot j+b) \\[3pt]&\quad+\, O\bigg( \frac{1}{ M } \bigg)\\[3pt]&= \frac{1}{q M } \sum_{j=1} ^{M} \sum_{b=r} ^{q +r-1} \gamma(q \cdot j+c) \cdot a(q\cdot j+b) + O\bigg( \frac{ q }{ M } \bigg) \\[3pt]&= A_{r,c} ^{q ,M} + O\bigg( \frac{ q }{ M } \bigg). \end{align*} $$
Indeed, the first equality follows since
$g(T^{n} x)$
and
$a_{n}$
are both bounded sequences; in the third equality, we use Lemma 2.1(1); and in the fourth equality, we are using the previous equation array and the definition of x. This definition along with the definition of
$s_{k}^{(\ell )}$
justify the fifth equality. The last equality is simply the definition of
$A_{r,c}^{q ,M}$
.
Remark 2.7. In the setup of Lemma 2.6, we may similarly find another
$x \in P^{(\ell )} \times \lbrace -1,0,1\rbrace ^{\mathbb {Z}}$
that satisfies the conclusion of Lemma 2.6, but for
$-A_{r,c}^{q_{k^{\prime }}^{(\ell )}, M_{k^{\prime }}^{(\ell )} }$
. Indeed, this follows from the very same proof by picking
$x \in P^{(\ell )} \times \lbrace -1,0,1\rbrace ^{\mathbb {Z}}$
to be any element such that for every
$ q_{k^{\prime }}^{(\ell )} \leq n<q_{k^{\prime }+1}^{(\ell )}$
,
$$ \begin{align*}x (n) = ( s_{k^{\prime}} ^{(\ell)}(n-r), -\gamma( q_{k^{\prime}} ^{(\ell)} \cdot n+c) ).\end{align*} $$
We will also require the following lemma.
Lemma 2.8. For every j large enough, there is either some
$c\in [0 , q_{k^{\prime }}^{(i^{\prime })} )$
such that
$$ \begin{align} A_{c,c} ^{q_{k^{\prime}}^{(i^{\prime})} ,M_{k^{\prime}}^{(i^{\prime})} } \geq \frac{\theta}{8q_{k^{\prime}} ^{(i^{\prime})}} , \end{align} $$
or some
$d\in [0 , q_{k^{\prime }}^{(i^{\prime }+2)} )$
with
$$ \begin{align*} -A_{d+1,d} ^{q_{k^{\prime}}^{(i^{\prime}+2)}, M_{k^{\prime}}^{(i^{\prime}+2)}} \geq \frac{ \theta }{8q_{k^{\prime}} ^{(i^{\prime})}}.\end{align*} $$
Proof. In this proof, we again suppress the
$i^{\prime },k^{\prime },u$
in our notation, and write instead
$q, M,$
for
$q_{k^{\prime }}^{(i^{\prime })}$
and
$M_{k^{\prime }}^{(i^{\prime })}$
, respectively (the terms corresponding to
$i^{\prime }+2$
will come up in the proof later). Now, for every
$c,r \in [0, q]$
,
$$ \begin{align*}\sum_{c=0} ^{q-1} A_{c+r,c} ^{q,M} = \frac{1}{qM} \sum_{m=1} ^{qM} \gamma(m)\cdot ( a(m+r)+\cdots+a(m+r+q-1) ) + O\bigg( \frac{1}{M} \bigg).\end{align*} $$
So,
$$ \begin{align*}qM \cdot \sum_{c=0} ^{q-1} A_{c,c} ^{q,M} = \sum_{m=1} ^{qM} \gamma(m)\cdot ( a(m)+\cdots+a(m+q-1) )+ O( q )\end{align*} $$
and
$$ \begin{align*} &(q-1) \bigg[ \frac{q M}{q-1} \bigg] \sum_{c=1} ^{q-1} A_{c+1,c} ^{q-1, [ {q M}/({q-1}) ] }\\ &\quad= \sum_{m=1} ^{qM} \gamma(m)\cdot ( a(m+1)+\cdots+a(m+q-1) )+ O( q^{2} ).\end{align*} $$
Combining the last two displayed equations,
$$ \begin{align*} &qM \cdot \sum_{c=0} ^{q-1} A_{c,c} ^{q,M} - (q-1) \bigg[ \frac{q M}{q-1} \bigg] \sum_{c=1} ^{q-1} A_{c+1,c} ^{q-1, [ {q M}/({q-1}) ] } \\ &\quad= \sum_{m=1} ^{qM} \gamma(m) a(m) +O( q^{2} ) \geq \theta/2 \cdot qM+O( q^{2} ).\end{align*} $$
It follows that, assuming q is large enough and via equation (4),
$$ \begin{align*}\sum_{c=0} ^{q-1} A_{c,c} ^{q,M} - \sum_{d=1} ^{q-1} A_{d+1,d} ^{q-1, [ {qM}/({q-1}) ] } \geq \theta/2- O\bigg( \frac{q}{M} \bigg) \geq \theta/2- O\bigg( \frac{1}{q^{2}} \bigg) \geq \theta/4.\end{align*} $$
Recalling our definition of
$q_{k^{\prime }}^{(i^{\prime }+2)}$
and
$M_{k^{\prime }}^{(i^{\prime }+2)}$
, this implies the lemma.
2.4 Construction of the point and system as in Theorem 1.2
Recalling Lemma 2.8, by perhaps moving to a further subsequence, we may assume that the inequality from Lemma 2.8 is always given by the term corresponding to
$q_{k^{\prime }}^{(i^{\prime }+2u)}$
, where
$u=u(j)$
is either
$0$
or
$1$
, and both the quantities
$i^{\prime }=i(j)$
(defined in Definition 2.5) and u are assumed to be constant in j. Let us denote this constant value
$i^{\prime }+2u \in \lbrace 0,1,2,3\rbrace $
by
$\ell $
. Recalling Definition 2.5, and passing to a subsequence if needed, we assume that the map
$j\mapsto k(j)=k^{\prime }$
is injective.
We now construct a point
$x^{(\ell )}\in P^{(\ell )} \times \lbrace -1,0,1\rbrace ^{\mathbb {Z}} \subseteq X_{\ell }$
as follows. For every
$j\in \mathbb {N}$
and
$q_{k(j)}^{(\ell )} \leq n < q_{k(j)+1}^{(\ell )}$
,
$x^{(\ell )} (n)=x(n)$
, where x is the element as in Lemma 2.6 (if
$u= 0$
) or Remark 2.7 (if
$u =1$
), corresponding to j,
$\ell $
as in the paragraph above, and either
$r=c$
and c (if
$u=0$
) or
$r=d+1$
and
$c=d$
(if
$u=1$
) yielding the inequality from Lemma 2.8. Note that here we need the map
$j\mapsto k(j)$
to be injective so this is well defined (that is, the intervals
$[q_{k(j)}^{(\ell )}, \, q_{k(j)+1}^{(\ell )})$
do not overlap). Note that so far we have only specified the digits
$n \in \bigcup _{j\in \mathbb {N}} [q_{k(j)}^{(\ell )}, \, q_{k(j)+1}^{(\ell )})$
, and (since we have passed to a subsequence) it is possible that this union does not cover all of
$\mathbb {N}$
. So, for all digits not covered, we make some choice that ensures
$x^{(\ell )} \in P^{(\ell )} \times \lbrace -1,0,1\rbrace ^{\mathbb {Z}}$
. Note that by Lemma 2.6 and the construction of
$P^{(\ell )}$
, such a choice is readily available.
We now take our space to be
$$ \begin{align} X:= X_{0} \times X_{1} \times X_{2} \times X_{3} \times \lbrace 0,1,2,3\rbrace,\end{align} $$
with the self-mapping
$\hat {T} \in \mathcal {C}(X)$
being
$$ \begin{align*}\hat{T}(p^{(0)}, p^{(1)}, p^{(2)}, p^{(3)}, i) = (T p^{(0)}, T p^{(1)}, Tp^{(2)}, Tp^{(3)}, i).\end{align*} $$
The function
$f\in \mathcal {C}(X)$
is taken to be
$$ \begin{align*}f( (y^{(0)}, z^{(0)}), (y^{(1)}, z^{(1)}), (y^{(2)}, z^{(2)}), (y^{(3)}, z^{(3)}), i) = z_{0} ^{(i)}.\end{align*} $$
We next choose our point x to be any
$x\in X$
such that its projection to
$X_{\ell }$
is
$x^{(\ell )}$
, and its projection to
$\lbrace 0,1,2,3\rbrace $
is
$\ell $
.
We now prove Theorem 1.2(1) via the following two claims.
Lemma 2.9. We have
$h(X, \hat {T})=0$
.
Proof. By Claim 2.4, each factor in the product space X has zero entropy, which implies the assertion via standard arguments.
Lemma 2.10. For all j large enough,
$$ \begin{align*} \frac{1}{N_{j}} \sum_{n=1} ^{N_{j}} f(\hat{T}^{n} x) a(n) \geq \theta\cdot \tau(N_{j}).\end{align*} $$
In particular,
$$ \begin{align*}\limsup_{N\rightarrow \infty} \frac{ ({1}/{N})\! \sum_{n=1} ^{N} f(\hat{T}^{n} x) a(n)}{\tau(N)}>0.\end{align*} $$
Proof. Fix j large, and let us write
$N, q, M, x$
, suppressing the dependence on
$k^{\prime },\ell ,j$
(except in parts of the proof where we wish to emphasize this dependence). Note that
$$ \begin{align*}q M \in [N-q, N].\end{align*} $$
Now,
$$ \begin{align*} \frac{1}{N} \sum_{n=1} ^{N} f(\hat{T}^{n} x) a(n) &= \frac{1}{q M } \sum_{n=1} ^{q M} f(\hat{T}^{n} x) a(n)+ O\bigg( \frac{1}{ M} \bigg)\\&= \frac{1}{q M } \bigg( \sum_{n=1} ^{q -1} f(\hat{T}^{n} x) a(n) + \sum_{n=q} ^{q M } f(\hat{T}^{n} x) a(n) \bigg)+ O\bigg( \frac{1}{ M} \bigg)\\&= \frac{1}{q M } \bigg( \sum_{n=1} ^{q -1} \!f(\hat{T}^{n} x) a(n) + \!\sum_{n=1} ^{q M } g(T^{n} x^{(\ell)} ) a(n) - \!\sum_{n=1} ^{q -1} g(T^{n} x^{(\ell)} ) a(n)\! \bigg)\\&\quad +\, O\bigg( \frac{1}{ M} \bigg)\\&= \frac{1}{q_{k^{\prime}} ^{(\ell)} M_{k^{\prime}} ^{(\ell)} } \sum_{n=1} ^{q_{k^{\prime}}^{(\ell)} M_{k^{\prime}}^{(\ell)} } g(T^{n} x^{(\ell)}) a(n) + O\bigg( \frac{ 1 }{M_{k^{\prime}} ^{(\ell)}} \bigg)\\&\geq \frac{\theta}{8q_{k^{\prime}} ^{(i^{\prime})}} + O\bigg( \frac{ q_{k^{\prime}} ^{(\ell)} }{M_{k^{\prime}} ^{(\ell)}} \bigg). \end{align*} $$
Note that in the third equality, we are again using Lemma 2.3 in a similar fashion to the proof of Lemma 2.6, which is allowed since
$x^{(\ell )}\in P^{(\ell )} \times \lbrace -1,0,1\rbrace ^{\mathbb {Z}}$
. For the last inequality, we are using Lemmas 2.8 and 2.6 along with the definition of x.
We conclude that
$$ \begin{align*}\frac{1}{N_{j}} \sum_{n=1} ^{N_{j}} f(\hat{T}^{n} x) a(n) \geq \frac{\theta}{8q_{k^{\prime}} ^{(i^{\prime})}} + O\bigg( \frac{ q_{k^{\prime}} ^{(\ell)} }{M_{k^{\prime}} ^{(\ell)}} \bigg).\end{align*} $$
By equation (4),
$$ \begin{align*}O\bigg( \frac{ q_{k^{\prime}} ^{(\ell)} }{M_{k^{\prime}} ^{(\ell)}} \bigg) \leq O\bigg( \bigg( \frac{1}{q_{k^{\prime}} ^{(i^{\prime})}} \bigg)^{2} \bigg),\end{align*} $$
and so, as long as j is large enough,
$$ \begin{align*}\frac{1}{N_{j}} \sum_{n=0} ^{N_{j}-1} f(\hat{T}^{n} x) a(n) \geq \frac{\theta}{16q_{k^{\prime}} ^{(i^{\prime})}}.\end{align*} $$
Finally, it follows from our choice of
$N_{j}$
that
$N_{j}$
is larger than the element of the sequence
$q_{k} /3$
that comes after
$q_{k^{\prime }}^{(i^{\prime })} /3$
. So, by the choice of the sequence
$q_{k}$
,
$$ \begin{align*}\frac{1}{16q_{k^{\prime}} ^{(i^{\prime})}} \geq \tau(N_{j}).\end{align*} $$
Combining the last two displayed equations implies the claim.
3 Proof of Theorem 1.2(2).
In this section, we prove Theorem 1.2(2). That is, we show that the system
$(X, \hat {T})$
given in equation (6) satisfies the Möbius disjointness conjecture in equation (1). The proof will be an application of Matomäki–Radziwiłł’s bound [Reference Matomäki and Radziwiłł13] on averages of multiplicative functions along short intervals. The Matomäki–Radziwiłł bound as well as its extension by Matomäki, Radziwiłł and Tao [Reference Matomäki, Radziwiłł and Tao14] have recently become a powerful tool to establish Möbius disjointness for systems with strong periodic behavior.
Denote a point
$x\in X$
as
$$ \begin{align*}(x^{(0)},x^{(1)},x^{(2)},x^{(3)},i) \text{ where } x^{(\ell)}=(y^{(\ell)},z^{(\ell)}).\end{align*} $$
For each
$p=(y,z)\in \{-1,0,1\}^{\mathbb N}\times \{-1,0,1\}^{\mathbb Z}$
and
$M\in \mathbb N$
, denote by
$[p]_{M}$
the truncation
$$ \begin{align*}[p]_{M}:=((y_{1},\ldots,y_{M}),(z_{-M},\ldots,z_{M})).\end{align*} $$
Write
$\mathcal C_{M} (X)$
for the space of cylinder functions
$f(x)$
that only depends on
$([x^{(\ell )}]_{M})_{0\leq \ell \leq 3}$
and the fifth coordinate
$i \in \lbrace 0,1,2,3 \rbrace $
. Then
$\bigcup _{M=1}^{\infty }\mathcal C_{M} (X)$
is dense in
$\mathcal C(X)$
with respect to
$C^{0}$
norm. In consequence, it suffices to verify equation (1) for all cylinder functions
$f \in \mathcal C_{M}(X)$
for every M.
The main technical lemma that we need is the following.
Lemma 3.1. For all
$0\leq \ell \leq 3$
and
$M, H\in \mathbb N$
, and
$x\in X$
, there exists a set
$\Lambda ^{(\ell )}(M,H,x) \subseteq \mathbb N$
that satisfies:
-
(1)
$\lim _{N\to \infty }( 1/N)\#(\{1,\ldots , N\}\cap \Lambda ^{(\ell )}(M,H,x))=1$
; -
(2) for all
$n\in \Lambda ^{(\ell )}(M,H,x)$
,
$[T^{n+h}x^{(\ell )}]_{M}$
is constant for
$0\leq h\leq H-1$
.
Proof. Since
$$ \begin{align*}x^{(\ell)}\in X_{\ell}= \text{cl} \bigg(\bigcup_{b\in\mathbb N {}_{0}} T^{b}(P^{(\ell)}\times\{-1,0,1\}^{\mathbb Z})\bigg),\end{align*} $$
for each
$\ell $
and all
$N\in \mathbb N_{0}$
, there exists
$x^{(N,\ell )}\in \bigcup _{b\in \mathbb N_{0}} T^{b}(P^{(\ell )}\times \{-1,0,1\}^{\mathbb Z})$
such that
$$ \begin{align*}[x^{(N,\ell)}]_{N}=[x^{(\ell)}]_{N} \quad\text{for all } n\leq N.\end{align*} $$
We also choose
$b^{(N,\ell )}\in \mathbb N_{0}$
and
$\tilde x^{(N,\ell )}\in P^{(\ell )}\times \{-1,0,1\}^{\mathbb Z}$
such that
$x^{(N,\ell )}=T^{b^{(N,\ell )}}\tilde x^{(N,\ell )}$
.
Then, for
$1\leq n\leq N$
and
$0\leq h\leq H-1$
,
$$ \begin{align*}[T^{n+h}x^{(\ell)}]_{M}=[T^{n+h}x^{(N+H+M,\ell)}]_{M}=[T^{n+b^{(N+H+M,\ell)}+h}\tilde x^{(N+H+M,\ell)}]_{M}.\end{align*} $$
Therefore, by Lemma 2.1(1),
$[T^{n+h}x^{(\ell )}]_{M}$
is constant for
$0\leq h\leq H-1$
if
$$ \begin{align}\Pi_{1}\tilde x^{(N+H+M,\ell)}(n+b^{(N,\ell)}+h^{\prime})=0 \quad\text{for all } 0\leq h^{\prime}\leq H+M-1.\end{align} $$
Since
$ \tilde x^{(N+H+M,\ell )}\in P^{(\ell )}\kern-1pt \times\kern-1pt \{-1,0,1\}^{\mathbb Z}$
, for every
$k \kern-1pt \in\kern-1pt \mathbb {N}$
, there is some
$0\kern-1pt \leq r_{k}^{(\ell )} \kern-1.5pt \leq q_{k}^{(\ell )}-1$
such that
$$ \begin{align*}\Pi_{1}\tilde x^{(N+H+M,\ell)}(n^{\prime})=s_{k}^{(\ell)}(n^{\prime}- r_{k}^{(\ell)}) \quad\text{for } q_{k}^{(\ell)}\leq n^{\prime}<q_{k+1}^{(\ell)}.\end{align*} $$
In particular,
$\Pi _{1}\tilde x^{(N+H+M,\ell )}(n^{\prime })=0$
for all
$q_{k}^{(\ell )}\leq n^{\prime }<q_{k+1}^{(\ell )}$
with
$n^{\prime }\not \equiv r_{k}^{(\ell )} (\text {mod } q_{k}^{(\ell )})$
.
It follows that for each k, equation (7) holds on the set
$$ \begin{align*}\begin{aligned}\Lambda_{N,k}^{(\ell)}(M,H,x)&:=\{1\leq n\leq N: q_{k}^{(\ell)}\leq n+b^{(N+H+M,\ell)}\leq q_{k+1}^{(\ell)}-H-M;\\ &\ \qquad n+b^{(N+H+M,\ell)}\not\equiv r_{k}^{(\ell)}-H-M+1, \ldots, r_{k}^{(\ell)}-1, r_{k}^{(\ell)} (\text{mod } q_{k}^{(\ell)})\}.\end{aligned}\end{align*} $$
Set
$\Lambda _{N}^{(\ell )}(M,H,x)=\bigcup _{k=1}^{\infty }\Lambda _{N,k}^{(\ell )}(M,H,x)\subseteq \{1,\ldots , N\}$
. Then
$[T^{n+h}x^{(\ell )}]_{M}$
is constant for
$0\leq h\leq H-1$
if
$n\in \Lambda ^{(\ell )}(M,H,x)$
.
Finally,
$$ \begin{align*}\lim_{N\to\infty}\frac 1N\#(\{1,\ldots, N\}\cap\Lambda^{(\ell)} _{N} (M,H,x))=1\end{align*} $$
because of the following facts: H and M are fixed,
$b^{(N+H+M,\ell )}\geq 0$
,
$\lim _{k\to \infty }q_{k}^{(\ell )}=\infty $
, and
$\lim _{k\to \infty }({q_{k+1}^{(\ell )}}/{q_{k}^{(\ell )}})= \infty $
. We conclude the proof by defining
$$ \begin{align*}\Lambda^{(\ell)}(M,H,x):=\bigcup_{N=1}^{\infty}\Lambda_{N}^{(\ell)}(M,H,x).\\[-4.8pc] \end{align*} $$
Corollary 3.2. For all
$ M, H\in \mathbb N$
, and
$x\in X$
, there exists a set
$\Lambda (M,H,x)\subseteq \mathbb N$
that satisfies the following:
-
(1)
$\lim _{N\to \infty }( 1/N)\#(\{1,\ldots , N\}\cap \Lambda (M,H,x))=1$
; -
(2) for all
$f\in \mathcal C_{M}(X)$
and any given
$n\in \Lambda (M,H,x)$
,
$ f(\hat {T}^{n+h}x)$
is constant for
$0\leq h\leq H-1$
.
Proof. Let
$\Lambda ^{(\ell )}(M,H,x)$
be as in Lemma 3.1, and set
$$ \begin{align*}\Lambda(M,H,x):=\bigcap_{0\leq \ell\leq 3}\Lambda^{(\ell)}(M,H,x)\subset\mathbb N.\end{align*} $$
Then clearly, we still have
$$ \begin{align*}\lim_{N\to\infty}\frac 1N\#(\{1,\ldots, N\}\cap\Lambda(M,H,x))=1.\end{align*} $$
Next, let
$f\in \mathcal C_{M} (X)$
. Since
$f(\hat {T}^{n+h}x)$
only depends on
$([T^{n+h}x^{(\ell )}]_{M})_{0\leq \ell \leq 3}$
and the i coordinate (that does not change when we apply
$\hat {T}$
), given
$n\in \Lambda ^{(\ell )}(i,M, H, x)$
, it is constant for
$0\leq h\leq H-1$
by Lemma 3.1.
We are now ready to establish Möbius disjointness.
Proof of Theorem 1.2(2)
As remarked in the beginning of this section, we may assume
$f\in \mathcal C_{M}(X)$
for some M and
$|f|\leq 1$
. Let
$x\in X$
. Then for a fixed H, as
$N\to \infty $
,
$$ \begin{align*} \begin{aligned} \bigg|\frac1N\sum_{n=1}^{N}f(\hat{T}^{n}x)\mu(n)\bigg| &=\bigg|\frac1N\sum_{n=1}^{N}\frac 1H\sum_{h=0}^{H-1}f(\hat{T}^{n+h}x)\mu(n)\bigg|+O\bigg(\frac HN\bigg)\\ &=\bigg|\frac1N\sum_{\substack{1\leq n\leq N\\n\in\Lambda(M,H,x)}}\frac1H \sum_{h=0}^{H-1}f(\hat{T}^{n+h}x)\mu(n)\bigg|+o_{H}(1)+O\bigg(\frac HN\bigg)\\ &\leq \frac1N \!\sum_{\substack{1\leq n\leq N\\n\in\Lambda(M,H,x)}} \!\bigg|\frac1H \sum_{h=0}^{H-1}f(\hat{T}^{n+h}x)\mu(n+h)\bigg|+o_{H}(1)+O\bigg(\frac HN\bigg). \end{aligned} \end{align*} $$
Here,
$o_{H}(1)$
stands for a quantity that tends to
$0$
as
$N\to \infty $
for a fixed H.
By Corollary 3.2,
$f(\hat {T}^{n+h}x)=f(\hat {T}^{n} x)$
for every
$n\in \Lambda (M,H,x)$
and
$0\leq h\leq H-1$
. So,
$$ \begin{align*} \begin{aligned} \bigg|\frac1N\sum_{n=1}^{N}f(\hat{T}^{n}x)\mu(n)\bigg| &\leq \frac1N\sum_{\substack{1\leq n\leq N\\n\in\Lambda(M,H,x)}}\bigg|\frac1H \sum_{h=0}^{H-1}f(\hat{T}^{n}x)\mu(n+h)\bigg|+o_{H}(1)+O\bigg(\frac HN\bigg)\\ &\leq \frac1N\sum_{\substack{1\leq n\leq N\\n\in\Lambda(M,H,x)}}\bigg|\frac1H \sum_{h=0}^{H-1}\mu(n+h)\bigg|+o_{H}(1)+O\bigg(\frac HN\bigg)\\ &\leq \frac1N\sum_{n=1}^{N}\bigg|\frac1H \sum_{h=0}^{H-1}\mu(n+h)\bigg|+o_{H}(1)+O\bigg(\frac HN\bigg)\\ &= O\bigg(\bigg(\frac1{\log H}\bigg)^{0.01}+\bigg(\frac{\log H}{\log N}\bigg)^{0.01}\bigg)+o_{H}(1)+O\bigg(\frac HN\bigg). \end{aligned} \end{align*} $$
The last step is given by [Reference Matomäki and Radziwiłł13, Theorem 1].
By letting
$H\to \infty $
first, and then
$N\to \infty $
for each fixed H, we see that
$$ \begin{align*}\frac1N\sum_{n=1}^{N}f(\hat T^{n}x)\mu(n)=o(1) \quad\text{as}\ N\to\infty.\\[-4pc] \end{align*} $$
Acknowledgments
We thank the anonymous referee for helpful comments. Z.W. was supported by NSF grant DMS-1753042. A. A. acknowledges support from the Hebrew University of Jerusalem, where some of this research was done.
Open access
