Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-18T15:40:47.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Affine invariant submanifolds with completely degenerate Kontsevich–Zorich spectrum

Published online by Cambridge University Press:  04 July 2016

DAVID AULICINO
DAVID AULICINO*
Affiliation:
University of Chicago, Mathematics, 5734 University Avenue, Chicago, IL 60637-1514, USA email aulicino@math.uchicago.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that if the Lyapunov spectrum of the Kontsevich–Zorich cocycle over an affine 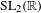$\text{SL}_{2}(\mathbb{R})$-invariant submanifold is completely degenerate, i.e. if 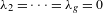$\unicode[STIX]{x1D706}_{2}=\cdots =\unicode[STIX]{x1D706}_{g}=0$, then the submanifold must be an arithmetic Teichmüller curve in the moduli space of Abelian differentials over surfaces of genus three, four, or five. As a corollary, we prove that there is at most a finite number of such Teichmüller curves.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 1 , February 2018 , pp. 10 - 33
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, J., Bufetov, A., Eskin, A. and Mirzakhani, M.. Lattice point asymptotics and volume growth on Teichmüller space. Duke Math. J. 161(6) (2012), 1055–1111.Google Scholar
Avila, A., Eskin, A. and Möller, M.. Symplectic and isometric SL(2,R) invariant subbundles of the Hodge bundle, Preprint, 2012, 1–16, arXiv:1209.2854v1.Google Scholar
Avila, A., Matheus, C. and Yoccoz, J.-C.. SL (2, ℝ)-invariant probability measures on the moduli spaces of translation surfaces are regular. Geom. Funct. Anal. 23(6) (2013), 1705–1729.CrossRefGoogle Scholar
Aulicino, D.. Affine manifolds and zero Lyapunov exponents in genus 3. Geom. Funct. Anal. 25(5) (2015), 1333–1370.CrossRefGoogle Scholar
Aulicino, D.. Teichmüller discs with completely degenerate Kontsevich–Zorich spectrum. Comment. Math. Helv. 90(3) (2015), 573–643.Google Scholar
Avila, A. and Viana, M.. Simplicity of Lyapunov spectra: proof of the Zorich–Kontsevich conjecture. Acta Math. 198(1) (2007), 1–56.Google Scholar
Calta, K.. Veech surfaces and complete periodicity in genus two. J. Amer. Math. Soc. 17(4) (2004), 871–908.Google Scholar
Eskin, A., Kontsevich, M. and Zorich, A.. Sum of Lyapunov exponents of the Hodge bundle with respect to the Teichmüller geodesic flow. Publ. Math. Inst. Hautes Études Sci. 120 (2014), 207–333.Google Scholar
Eskin, A. and Mirzakhani, M.. Invariant and stationary measures for the $\text{SL}(2,\mathbb{R})$ action on moduli space, Preprint, 2013, 1–171, arXiv:1302.3320.Google Scholar
Eskin, A., Mirzakhani, M. and Mohammadi, A.. Isolation, equidistribution, and orbit closures for the SL(2, ℝ) action on moduli space. Ann. of Math. (2) 182(2) (2015), 673–721.Google Scholar
Eskin, A., Masur, H. and Schmoll, M.. Billiards in rectangles with barriers. Duke Math. J. 118(3) (2003), 427–463.Google Scholar
Fay, J. D.. Theta Functions on Riemann Surfaces (Lecture Notes in Mathematics, 352) . Springer, Berlin, 1973.Google Scholar
Forni, G., Matheus, C. and Zorich, A.. Square-tiled cyclic covers. J. Mod. Dyn. 5(2) (2011), 285–318.Google Scholar
Forni, G., Matheus, C. and Zorich, A.. Lyapunov spectrum of invariant subbundles of the Hodge bundle. Ergod. Th. & Dynam. Sys. 34(2) (2014), 353–408.Google Scholar
Forni, G., Matheus, C. and Zorich, A.. Zero Lyapunov exponents of the Hodge bundle. Comment. Math. Helv. 89(2) (2014), 489–535.Google Scholar
Forni, G.. Deviation of ergodic averages for area-preserving flows on surfaces of higher genus. Ann. of Math. (2) 155(1) (2002), 1–103.Google Scholar
Forni, G.. On the Lyapunov exponents of the Kontsevich–Zorich cocycle. Handbook of Dynamical Systems Vol. 1B. Elsevier B. V., Amsterdam, 2006, pp. 549–580.Google Scholar
Forni, G.. A geometric criterion for the nonuniform hyperbolicity of the Kontsevich–Zorich cocycle. J. Mod. Dyn. 5(2) (2011), 355–395, With an appendix by Carlos Matheus.Google Scholar
Gutkin, E. and Judge, C.. Affine mappings of translation surfaces: geometry and arithmetic. Duke Math. J. 103(2) (2000), 191–213.Google Scholar
Möller, M.. Shimura and Teichmüller curves. J. Mod. Dyn. 5(1) (2011), 1–32.Google Scholar
Mirzakhani, M. and Wright, A.. The boundary of an affine invariant submanifold, Preprint, 2015, 1–57, arXiv:1508.01446.Google Scholar
Smillie, J. and Weiss, B.. Minimal sets for flows on moduli space. Israel J. Math. 142 (2004), 249–260.Google Scholar
Veech, W. A.. Geometric realizations of hyperelliptic curves. Algorithms, Fractals, and Dynamics (Okayama/Kyoto, 1992). Plenum, New York, 1995, pp. 217–226.Google Scholar
Wright, A.. The field of definition of affine invariant submanifolds of the moduli space of abelian differentials. Geom. Topol. 18(3) (2014), 1323–1341.Google Scholar
Wright, A.. Cylinder deformations in orbit closures of translation surfaces. Geom. Topol. 19(1) (2015), 413–438.Google Scholar
Yamada, A.. Precise variational formulas for abelian differentials. Kodai Math. J. 3(1) (1980), 114–143.Google Scholar