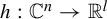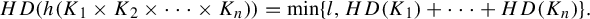1 Introduction
In this paper, we prove a version of the scale recurrence lemma of Moreira and Yoccoz (see [Reference Moreira and Yoccoz7, §3.2]) in the context of Cantor sets in the complex plane. We will use this new version, together with other results, to prove a dimension formula for projections of products of complex Cantor sets. More precisely, given conformal regular Cantor sets
![]() $K_1,\ldots ,K_n$
in
$K_1,\ldots ,K_n$
in
![]() $\mathbb {C}$
, and a
$\mathbb {C}$
, and a
![]() $C^1$
function
$C^1$
function
![]() $h:\mathbb {C}^{n}\to \mathbb {R}^{l}$
, we prove that, under natural hypothesis, one has
$h:\mathbb {C}^{n}\to \mathbb {R}^{l}$
, we prove that, under natural hypothesis, one has
Our results will be proved for conformal regular Cantor sets. Those are Cantor sets that are maximal invariant sets for an expanding map, whose derivative is conformal at the points in the Cantor set. Rigorous definitions will be given in §2. The investigation of such Cantor sets is important because they appear in the study of homoclinic bifurcations of automorphisms of
![]() $\mathbb {C}^2$
, as shown by Araújo and Moreira in [Reference Araújo and Moreira1]. We expect that conformal regular Cantor sets in
$\mathbb {C}^2$
, as shown by Araújo and Moreira in [Reference Araújo and Moreira1]. We expect that conformal regular Cantor sets in
![]() $\mathbb {C}$
will play a role in the study of homoclinic bifurcations of automorphisms of
$\mathbb {C}$
will play a role in the study of homoclinic bifurcations of automorphisms of
![]() $\mathbb {C}^2$
, similar to regular Cantor sets in
$\mathbb {C}^2$
, similar to regular Cantor sets in
![]() $\mathbb {R}$
in the study of homoclinic bifurcations of surface diffeomorphisms.
$\mathbb {R}$
in the study of homoclinic bifurcations of surface diffeomorphisms.
The study of homoclinic bifurcations has proved to be fruitful in the understanding of dynamics for surface diffeomorphisms. Complicated dynamical phenomena arise from them. For example, arbitrarily close to any diffeomorphism exhibiting a generic homoclinic tangency, there are open regions in which any diffeomorphism belonging to a residual set has an infinite number of sinks—this is the so-called Newhouse phenomenon. Looking for analogous results and using similar ideas to those of Newhouse, Buzzard [Reference Buzzard2] proved the existence of an open set of automorphisms of
![]() $\mathbb {C}^2$
with stable homoclinic tangencies.
$\mathbb {C}^2$
with stable homoclinic tangencies.
The scale recurrence lemma was an important step in the solution to the Palis conjecture, about the arithmetic difference of Cantor sets, by Moreira and Yoccoz. They proved that there is an open and dense subset, inside the set of pairs of regular Cantor sets with sum of Hausdorff dimensions bigger than one, such that any pair
![]() $(K_1,K_2)$
in this subset verifies
$(K_1,K_2)$
in this subset verifies
![]() $int(K_1-K_2)\neq \emptyset $
. The theorem of Moreira and Yoccoz is for regular Cantor sets in the real line. Together with Araujo, we are close to proving an analogous result for conformal regular Cantor sets in the complex plane. The scale recurrence lemma in these papers is a fundamental tool for this work in progress; from our point of view, this is the main motivation for proving the conformal version of the lemma.
$int(K_1-K_2)\neq \emptyset $
. The theorem of Moreira and Yoccoz is for regular Cantor sets in the real line. Together with Araujo, we are close to proving an analogous result for conformal regular Cantor sets in the complex plane. The scale recurrence lemma in these papers is a fundamental tool for this work in progress; from our point of view, this is the main motivation for proving the conformal version of the lemma.
Furthermore, Moreira and Yoccoz were able to use their solution to the Palis conjecture in the study of homoclinic bifurcations for surface diffeomorphisms (see [Reference Moreira and Yoccoz9]). They proved that given a surface diffeomorphism F with a homoclinic quadratic tangency associated to a horseshoe with dimension larger than one, the set of diffeomorphisms close to F presenting a stable tangency has positive density at F. One of the main reasons to study conformal regular Cantor sets is to apply the ideas in [Reference Moreira and Yoccoz9] to the context of homoclinic bifurcations of automorphisms of
![]() $\mathbb {C}^2$
. The work [Reference Araújo and Moreira1] already proves that this approach is rewarding; it shows that Buzzard’s example [Reference Buzzard2] can be recast in terms of the theory of conformal Cantor sets (where the concepts of limit geometries and recurrent compact set are applied).
$\mathbb {C}^2$
. The work [Reference Araújo and Moreira1] already proves that this approach is rewarding; it shows that Buzzard’s example [Reference Buzzard2] can be recast in terms of the theory of conformal Cantor sets (where the concepts of limit geometries and recurrent compact set are applied).
Another development in the subject was given by Lopez [Reference Lopez4]. He generalized the work [Reference Moreira and Yoccoz7] for a product of several Cantor sets in the real line. In this paper, we will consider a scale recurrence lemma for a product of several Cantor sets in the complex plane.
In brief, we believe that the study of conformal regular Cantor sets plays an important role in the theory of dynamics of automorphisms of
![]() $\mathbb {C}^2$
. We think that such Cantor sets should be further investigated, as we are convinced that the scale recurrence lemma is a key step towards a complex version of Palis’s conjecture, and this will have implications in the bifurcation theory of automorphisms of
$\mathbb {C}^2$
. We think that such Cantor sets should be further investigated, as we are convinced that the scale recurrence lemma is a key step towards a complex version of Palis’s conjecture, and this will have implications in the bifurcation theory of automorphisms of
![]() $\mathbb{C}^2$
.
$\mathbb{C}^2$
.
At the same time, we have the dimension formula as an application of the scale recurrence lemma. The study of this type of dimension formulas is motivated by a classical theorem of Marstrand, generalized by Mattila and others. Denote by
![]() $G(m,l)$
the set of l-dimensional linear subspaces of
$G(m,l)$
the set of l-dimensional linear subspaces of
![]() $\mathbb {R}^m$
and for
$\mathbb {R}^m$
and for
![]() $s\in G(m,l)$
, denote by
$s\in G(m,l)$
, denote by
![]() $\pi _s$
the orthogonal projection on s. The Marstrand theorem states that given
$\pi _s$
the orthogonal projection on s. The Marstrand theorem states that given
![]() $F\subset \mathbb {R}^m$
, a Borel subset, we have
$F\subset \mathbb {R}^m$
, a Borel subset, we have
for almost all
![]() $s\in G(m,l)$
, with respect to a volume measure on
$s\in G(m,l)$
, with respect to a volume measure on
![]() $G(m,l)$
. In the particular case when
$G(m,l)$
. In the particular case when
![]() $F=K_1\times \cdots \times K_n$
is a product of regular Cantor sets, one has
$F=K_1\times \cdots \times K_n$
is a product of regular Cantor sets, one has
![]() $HD(K_1\times \cdots \times K_n)=HD(K_1)+\cdots +HD(K_n)$
. Thus, our formula, equation (1), corresponds to the Marstrand formula replacing
$HD(K_1\times \cdots \times K_n)=HD(K_1)+\cdots +HD(K_n)$
. Thus, our formula, equation (1), corresponds to the Marstrand formula replacing
![]() $\pi _s$
by h. The difference between our result and the classical Marstrand theorem is that our theorem is not an ‘almost all’ result; it holds under explicit generic conditions on the map h and the Cantor sets. The formal statement of the dimension formula proven in this paper is the following main theorem.
$\pi _s$
by h. The difference between our result and the classical Marstrand theorem is that our theorem is not an ‘almost all’ result; it holds under explicit generic conditions on the map h and the Cantor sets. The formal statement of the dimension formula proven in this paper is the following main theorem.
Theorem B. (Dimension formula)
Let
![]() $K_1,\ldots ,K_n$
be
$K_1,\ldots ,K_n$
be
![]() $C^m$
,
$C^m$
,
![]() $m\geq 2$
, conformal regular Cantor sets generated by expanding maps
$m\geq 2$
, conformal regular Cantor sets generated by expanding maps
![]() $g_1,\ldots ,g_n$
, respectively. Suppose all of them are not essentially affine. Assume that there exist periodic points
$g_1,\ldots ,g_n$
, respectively. Suppose all of them are not essentially affine. Assume that there exist periodic points
![]() $p_j \in K_j$
, with period
$p_j \in K_j$
, with period
![]() $n_j$
, for
$n_j$
, for
![]() $1\leq j\leq n$
, such that if we write
$1\leq j\leq n$
, such that if we write
![]() $Dg_j^{n_j}(p_j)=({1}/{r_j}) R_{-v_j},$
where
$Dg_j^{n_j}(p_j)=({1}/{r_j}) R_{-v_j},$
where
![]() $R_v$
is the rotation matrix by an angle
$R_v$
is the rotation matrix by an angle
![]() $v\in \mathbb {T}$
, then
$v\in \mathbb {T}$
, then
 $$ \begin{align*} (\log r_1,0,\ldots,0&;v_1,0,\ldots,0),\\ &\vdots \\ (0,\ldots,\log r_{n-1}&;0,\ldots,v_{n-1},0),\\ (-\log r_n,\ldots,-\log r_n &;0,\ldots,0,v_n), \end{align*} $$
$$ \begin{align*} (\log r_1,0,\ldots,0&;v_1,0,\ldots,0),\\ &\vdots \\ (0,\ldots,\log r_{n-1}&;0,\ldots,v_{n-1},0),\\ (-\log r_n,\ldots,-\log r_n &;0,\ldots,0,v_n), \end{align*} $$
generate a dense subgroup of
![]() $\mathbb {R}^{n-1}\times \mathbb {T}^{n}$
. Let h be any
$\mathbb {R}^{n-1}\times \mathbb {T}^{n}$
. Let h be any
![]() $C^{1}$
function defined on a neighborhood of
$C^{1}$
function defined on a neighborhood of
![]() $K_1\times \cdots \times K_n$
into
$K_1\times \cdots \times K_n$
into
![]() $\mathbb {R}^l$
such that there exists
$\mathbb {R}^l$
such that there exists
![]() $x_0\in K_1\times \cdots \times K_n$
where
$x_0\in K_1\times \cdots \times K_n$
where
![]() $Dh(x_0)$
verifies the transversality hypotheses. Then
$Dh(x_0)$
verifies the transversality hypotheses. Then
The transversality hypotheses mean that for any subset
![]() $A\subset \{1,\ldots ,n\}$
, the linear map
$A\subset \{1,\ldots ,n\}$
, the linear map
![]() $Dh(x_0): \mathbb {C}^n\to \mathbb {R}^l$
satisfies
$Dh(x_0): \mathbb {C}^n\to \mathbb {R}^l$
satisfies
This is the minimum assumption one needs to have the dimension formula for linear maps. Proper definitions of all other objects are given in the next section.
This type of problem has already been investigated by other authors, we mention some of them. Peres and Shmerkin [Reference Peres and Shmerkin11] proved that for
![]() $K_1, K_2 \subset \mathbb {R}$
attractors for self-affine iterated functions system (i.f.s.) given by maps
$K_1, K_2 \subset \mathbb {R}$
attractors for self-affine iterated functions system (i.f.s.) given by maps
![]() $\{r_ix+t_i\}_{i=1}^{n}$
,
$\{r_ix+t_i\}_{i=1}^{n}$
,
![]() $\{r_i'x+t_i'\}_{i=1}^{n'}$
, if there are
$\{r_i'x+t_i'\}_{i=1}^{n'}$
, if there are
![]() $j,k$
such that
$j,k$
such that
![]() $\log (r_j)/ \log (r_k')$
is irrational, then
$\log (r_j)/ \log (r_k')$
is irrational, then
for all
![]() $\unicode{x3bb} \neq 0$
.
$\unicode{x3bb} \neq 0$
.
However, Moreira [Reference Moreira8] studied the same formula for
![]() $K_1, K_2\subset \mathbb {R}$
regular Cantor sets. He proved that the formula holds provided one of the Cantor sets is not essentially affine. Moreira’s proof uses the scale recurrence lemma of [Reference Moreira and Yoccoz7].
$K_1, K_2\subset \mathbb {R}$
regular Cantor sets. He proved that the formula holds provided one of the Cantor sets is not essentially affine. Moreira’s proof uses the scale recurrence lemma of [Reference Moreira and Yoccoz7].
In another work, Hochman and Shmerkin [Reference Hochman and Shmerkin3] proved a dimension formula without assuming any type of affinity or non-affinity in the attractors or Cantor sets. They proved (in fact, this is a corollary of their main theorem) that for
![]() $K_1,\ldots ,K_n$
attractors for i.f.s. on
$K_1,\ldots ,K_n$
attractors for i.f.s. on
![]() $\mathbb {R}$
, one has
$\mathbb {R}$
, one has
for all
![]() $\unicode{x3bb} _i\neq 0$
,
$\unicode{x3bb} _i\neq 0$
,
![]() $i=1,\ldots ,n$
, provided that a certain set is dense in the group
$i=1,\ldots ,n$
, provided that a certain set is dense in the group
![]() $(\mathbb {R}^n,+)/\Delta $
, where
$(\mathbb {R}^n,+)/\Delta $
, where
![]() $\Delta $
is the diagonal. This set depends on the derivative of the contractions of the i.f.s. on periodic points. The technique used by Hochman and Shmerkin is different from the approach of Moreira.
$\Delta $
is the diagonal. This set depends on the derivative of the contractions of the i.f.s. on periodic points. The technique used by Hochman and Shmerkin is different from the approach of Moreira.
Apart from the motivations given by the Marstrand theorem and dynamical systems, there are other reasons to study sets of the form
![]() $K_1+K_2$
, where
$K_1+K_2$
, where
![]() $K_1, K_2$
are dynamically defined Cantor sets. There are applications in number theory as well. In [Reference Moreira6], Moreira used his dimension formula to prove that fractal dimensions of the Lagrange spectrum grow continuously. More precisely, he proved that the function
$K_1, K_2$
are dynamically defined Cantor sets. There are applications in number theory as well. In [Reference Moreira6], Moreira used his dimension formula to prove that fractal dimensions of the Lagrange spectrum grow continuously. More precisely, he proved that the function
where
![]() $L\subset \mathbb {R}$
is the Lagrange spectrum, is continuous.
$L\subset \mathbb {R}$
is the Lagrange spectrum, is continuous.
In this paper, we will adapt the methods used by Moreira and Yoccoz to the context of Cantor sets in the complex plane. We will consider an arbitrary finite number of Cantor sets, not just two. This will leave us facing different difficulties. First, we need to find the right definition for the renormalization operators and the right statement for the scale recurrence lemma. Those are mainly influenced by Lemma 3.1 and equation (2). However, the high dimensionality of the context requires a more detailed analysis. This can be seen in the proof of Proposition 3.1 and the use of Lemma 3.5. The proof of the conformal scale recurrence lemma requires a new type of hypothesis, the fact that each of the Cantor sets we are working with is not contained in a
![]() $C^1$
embedded curve. We call this property not essentially real, it is introduced in §2.4. Moreover, the proof of the scale recurrence lemma in [Reference Moreira and Yoccoz7] has a minor flaw, which we need to deal with; in §4, we comment on how to solve it.
$C^1$
embedded curve. We call this property not essentially real, it is introduced in §2.4. Moreover, the proof of the scale recurrence lemma in [Reference Moreira and Yoccoz7] has a minor flaw, which we need to deal with; in §4, we comment on how to solve it.
The paper is organized as follows. Section 2 contains basic definitions and results. In this section, we state, without proof, the scale recurrence lemma. Section 3 is dedicated to the proof of the dimension formula. Finally, in §4, we prove the scale recurrence lemma.
2 Basic definitions
In this section, we define the objects and present the principal tools that will play a role in the paper. Most of the proofs of the facts stated in this section follow from standard techniques, so we leave them without proof. For proofs, we refer the reader to [Reference Zamudio13, Ch. 1].
2.1 Conformal regular Cantor set
A
![]() $C^m$
regular Cantor set (or dynamically defined Cantor set) on the complex plane is given by the following data: a finite set
$C^m$
regular Cantor set (or dynamically defined Cantor set) on the complex plane is given by the following data: a finite set
![]() $\mathbb {A}$
of letters and a set
$\mathbb {A}$
of letters and a set
![]() $B\subset \mathbb {A}\times \mathbb {A}$
of admissible pairs, for each
$B\subset \mathbb {A}\times \mathbb {A}$
of admissible pairs, for each
![]() $a\in \mathbb {A}$
a compact connected set
$a\in \mathbb {A}$
a compact connected set
![]() $G(a)\subset \mathbb {C}$
, and a
$G(a)\subset \mathbb {C}$
, and a
![]() $C^m$
function
$C^m$
function
![]() $g:V\to \mathbb {C}$
defined in an open neighborhood V of
$g:V\to \mathbb {C}$
defined in an open neighborhood V of
![]() $\bigsqcup _{a\in \mathbb {A}} G(a)$
. This data must verify the following assumptions.
$\bigsqcup _{a\in \mathbb {A}} G(a)$
. This data must verify the following assumptions.
-
• The sets
 $G(a)$
,
$G(a)$
,
 $a\in \mathbb {A}$
, are pairwise disjoint.
$a\in \mathbb {A}$
, are pairwise disjoint. -
•
 $(a,b)\in B$
implies
$(a,b)\in B$
implies
 $G(b)\subset g(G(a))$
, otherwise
$G(b)\subset g(G(a))$
, otherwise
 $G(b)\cap g(G(a))=\emptyset $
.
$G(b)\cap g(G(a))=\emptyset $
. -
• For each
 $a\in \mathbb {A}$
, the restriction
$a\in \mathbb {A}$
, the restriction
 $g|_{G(a)}$
can be extended to a
$g|_{G(a)}$
can be extended to a
 $C^m$
diffeomorphism from an open neighborhood of
$C^m$
diffeomorphism from an open neighborhood of
 $G(a)$
onto its image such that
$G(a)$
onto its image such that
 $m(Dg)>1$
(where
$m(Dg)>1$
(where
 $m(A)=\inf _{v\neq 0} {|Av|}/{|v|}$
is the minimum norm of the linear map A).
$m(A)=\inf _{v\neq 0} {|Av|}/{|v|}$
is the minimum norm of the linear map A). -
• The subshift
 $(\Sigma ^+, \sigma )$
induced by B
$(\Sigma ^+, \sigma )$
induced by B  $$ \begin{align*}\Sigma^+=\{\underline{a}=(a_0,a_1,\ldots)\in \mathbb{A}^{\mathbb{N}}:(a_i,a_{i+1})\in B \text{ for all } i\geq 0\},\end{align*} $$
$$ \begin{align*}\Sigma^+=\{\underline{a}=(a_0,a_1,\ldots)\in \mathbb{A}^{\mathbb{N}}:(a_i,a_{i+1})\in B \text{ for all } i\geq 0\},\end{align*} $$
 $\sigma (a_0,a_1,a_2,\ldots )=(a_1,a_2,\ldots )$
is topologically mixing.
$\sigma (a_0,a_1,a_2,\ldots )=(a_1,a_2,\ldots )$
is topologically mixing.
Once we have such data, we can define a Cantor set (that is, totally disconnected, perfect compact set) on the complex plane
![]() $K=\bigcap _{n\geq 0}g^{-n}(\bigsqcup _{a\in \mathbb {A}} G(a))$
.
$K=\bigcap _{n\geq 0}g^{-n}(\bigsqcup _{a\in \mathbb {A}} G(a))$
.
We will say that the regular Cantor set is conformal if for all
![]() $x\in K$
, the linear map
$x\in K$
, the linear map
![]() $Dg(x):\mathbb {R}^2\to \mathbb {R}^2$
is conformal, that is,
$Dg(x):\mathbb {R}^2\to \mathbb {R}^2$
is conformal, that is,
![]() $m(Dg(x))=\|Dg(x)\|$
. The assumption that
$m(Dg(x))=\|Dg(x)\|$
. The assumption that
![]() $Dg$
is not necessarily conformal outside of the Cantor set was introduced by Araujo in his PhD thesis, where he studied Cantor sets associated to complex horseshoes for automorphisms of
$Dg$
is not necessarily conformal outside of the Cantor set was introduced by Araujo in his PhD thesis, where he studied Cantor sets associated to complex horseshoes for automorphisms of
![]() $\mathbb {C}^2$
. It plays an important role in the investigation of a complex version of Palis’s conjecture. We will write only K to represent all the data that are required to define a conformal regular Cantor set. All Cantor sets in this paper will be conformal regular Cantor sets; we will usually refer to them just as Cantor sets.
$\mathbb {C}^2$
. It plays an important role in the investigation of a complex version of Palis’s conjecture. We will write only K to represent all the data that are required to define a conformal regular Cantor set. All Cantor sets in this paper will be conformal regular Cantor sets; we will usually refer to them just as Cantor sets.
The degree of differentiability, m, can be any real number bigger than one. If m is not an integer, then g being
![]() $C^m$
means that it is
$C^m$
means that it is
![]() $C^{[m]}$
, where
$C^{[m]}$
, where
![]() $[m]$
is the integer part of m, and
$[m]$
is the integer part of m, and
![]() $D^{[m]}g$
is Holder with exponent
$D^{[m]}g$
is Holder with exponent
![]() $m-[m]$
. To prove our results, we will assume that
$m-[m]$
. To prove our results, we will assume that
![]() $m\geq 2$
.
$m\geq 2$
.
We can actually suppose that the sets
![]() $G(a)$
verify
$G(a)$
verify
![]() $G(a)=\overline {\mathrm {int}(G(a))}$
, this is a consequence of the next lemma.
$G(a)=\overline {\mathrm {int}(G(a))}$
, this is a consequence of the next lemma.
Lemma 2.1. Let K be a
![]() $C^m$
conformal Cantor set, then there exist a family of open and connected sets
$C^m$
conformal Cantor set, then there exist a family of open and connected sets
![]() $G^*(a)\subset \mathbb {C}$
for
$G^*(a)\subset \mathbb {C}$
for
![]() $a\in \mathbb {A}$
, such that we have the following properties.
$a\in \mathbb {A}$
, such that we have the following properties.
-
(i)
 $G(a)\subset G^*(a)$
, and
$G(a)\subset G^*(a)$
, and
 $g|_{G(a)}$
can be extended to an open neighborhood of
$g|_{G(a)}$
can be extended to an open neighborhood of
 $\overline {G^*(a)}$
such that it is a
$\overline {G^*(a)}$
such that it is a
 $C^m$
diffeomorphism from this neighborhood onto its image and
$C^m$
diffeomorphism from this neighborhood onto its image and
 $m(Dg)~>~1$
.
$m(Dg)~>~1$
. -
(ii) The sets
 $\overline {G^*(a)}$
,
$\overline {G^*(a)}$
,
 $a\in \mathbb {A}$
, are pairwise disjoint.
$a\in \mathbb {A}$
, are pairwise disjoint. -
(iii)
 $(a,b)\in B$
implies
$(a,b)\in B$
implies
 $\overline {G^*(b)}\subset g(G^*(a))$
, and
$\overline {G^*(b)}\subset g(G^*(a))$
, and
 $(a,b)\notin B$
implies
$(a,b)\notin B$
implies
 $\overline {G^*(b)}\cap \overline {g(G^*(a))}=\emptyset $
.
$\overline {G^*(b)}\cap \overline {g(G^*(a))}=\emptyset $
.
2.2 Limit geometry
Associated to K, we define the sets
![]() $\Sigma ^\textit{\,fin}=\{(a_0,\ldots ,a_n):(a_i,a_{i+1})\in B \}$
and
$\Sigma ^\textit{\,fin}=\{(a_0,\ldots ,a_n):(a_i,a_{i+1})\in B \}$
and
![]() $\Sigma ^{-}=\{(\ldots ,a_{-n},\ldots ,a_{-1},a_0): (a_i,a_{i+1})\in B\}$
.
$\Sigma ^{-}=\{(\ldots ,a_{-n},\ldots ,a_{-1},a_0): (a_i,a_{i+1})\in B\}$
.
Given
![]() $\underline {a}=(a_0,\ldots ,a_n)$
,
$\underline {a}=(a_0,\ldots ,a_n)$
,
![]() $\underline {b}=(b_0,\ldots ,b_m)$
,
$\underline {b}=(b_0,\ldots ,b_m)$
,
![]() $\underline {\theta }^1=(\ldots ,\theta ^1_{-1},\theta ^1_0)$
,
$\underline {\theta }^1=(\ldots ,\theta ^1_{-1},\theta ^1_0)$
,
![]() $\underline {\theta }^2=(\ldots ,\theta ^2_{-1},\theta ^2_0)$
, we will use the following notation.
$\underline {\theta }^2=(\ldots ,\theta ^2_{-1},\theta ^2_0)$
, we will use the following notation.
-
• If
 $a_n=b_0$
,
$a_n=b_0$
,
 $\underline {a}\underline {b}=(a_0,\ldots ,a_n,b_1\ldots ,b_m)$
.
$\underline {a}\underline {b}=(a_0,\ldots ,a_n,b_1\ldots ,b_m)$
. -
• If
 $\theta ^1_0=a_0$
,
$\theta ^1_0=a_0$
,
 $\underline {\theta }^1\underline {a}=(\ldots ,\theta ^1_{-1},\theta ^1_0,a_1,\ldots ,a_n)$
.
$\underline {\theta }^1\underline {a}=(\ldots ,\theta ^1_{-1},\theta ^1_0,a_1,\ldots ,a_n)$
. -
• If
 $\theta ^1_0=\theta ^2_0$
,
$\theta ^1_0=\theta ^2_0$
,
 $\underline {\theta }^1\wedge \underline {\theta }^2= (\theta ^1_{-j},\ldots ,\theta ^1_{0})$
, where j is such that
$\underline {\theta }^1\wedge \underline {\theta }^2= (\theta ^1_{-j},\ldots ,\theta ^1_{0})$
, where j is such that
 $\theta ^1_{-i}=\theta ^2_{-i}$
for all
$\theta ^1_{-i}=\theta ^2_{-i}$
for all
 $0\leq i\leq j$
, and
$0\leq i\leq j$
, and
 $\theta ^1_{-j-1}\neq \theta ^2_{-j-1}$
.
$\theta ^1_{-j-1}\neq \theta ^2_{-j-1}$
. -
• If
 $\theta ^1_0=a_n$
,
$\theta ^1_0=a_n$
,
 $\underline {\theta }^1\wedge \underline {a}= (\theta ^1_{-j},\ldots ,\theta ^1_{0})$
, where j is such that
$\underline {\theta }^1\wedge \underline {a}= (\theta ^1_{-j},\ldots ,\theta ^1_{0})$
, where j is such that
 $\theta ^1_{-i}=a_{n-i}$
for all
$\theta ^1_{-i}=a_{n-i}$
for all
 $0\leq i\leq j$
, and
$0\leq i\leq j$
, and
 $\theta ^1_{-j-1}\neq a_{n-j-1}$
.
$\theta ^1_{-j-1}\neq a_{n-j-1}$
.
For
![]() $\underline {a}=(a_0,\ldots ,a_n)\in \Sigma ^\textit{\,fin}$
, define
$\underline {a}=(a_0,\ldots ,a_n)\in \Sigma ^\textit{\,fin}$
, define
![]() $G(\underline {a})=\{x\in \bigsqcup _{a\in \mathbb {A}} G(a) : g^j(x)\in G(a_j), j=0, 1,\ldots ,n\},$
and the function
$G(\underline {a})=\{x\in \bigsqcup _{a\in \mathbb {A}} G(a) : g^j(x)\in G(a_j), j=0, 1,\ldots ,n\},$
and the function
![]() $f_{\underline {a}}:G(a_n) \to G(\underline {a})$
given by
$f_{\underline {a}}:G(a_n) \to G(\underline {a})$
given by
Denote by
![]() $K(\underline {a})$
the set
$K(\underline {a})$
the set
![]() $K\cap G(\underline {a})$
. For each
$K\cap G(\underline {a})$
. For each
![]() $a\in \mathbb {A}$
, we choose an arbitrary point
$a\in \mathbb {A}$
, we choose an arbitrary point
![]() $c_a \in K(a)$
. Using this, define
$c_a \in K(a)$
. Using this, define
![]() $c_{\underline {a}}\in G(\underline {a})$
by
$c_{\underline {a}}\in G(\underline {a})$
by
![]() $c_{\underline {a}}=f_{\underline {a}}(c_{a_n})$
.
$c_{\underline {a}}=f_{\underline {a}}(c_{a_n})$
.
Notice that
![]() $Df_{\underline {a}}(c_{a_n})$
is a conformal matrix in
$Df_{\underline {a}}(c_{a_n})$
is a conformal matrix in
![]() $\mathbb {R}^2$
, then it is equal to a positive real number times a rotation matrix, and denote the angle of rotation by
$\mathbb {R}^2$
, then it is equal to a positive real number times a rotation matrix, and denote the angle of rotation by
![]() $v_{\underline {a}}\in \mathbb {R}/(2\pi \mathbb {Z}).$
In this way, we have a preferred point and direction for each
$v_{\underline {a}}\in \mathbb {R}/(2\pi \mathbb {Z}).$
In this way, we have a preferred point and direction for each
![]() $G(\underline {a})$
. We also define
$G(\underline {a})$
. We also define
![]() $r_{\underline {a}}=\mathrm {diam}(G(\underline {a}))$
, where
$r_{\underline {a}}=\mathrm {diam}(G(\underline {a}))$
, where
![]() $\mathrm {diam}$
means diameter.
$\mathrm {diam}$
means diameter.
Given
![]() $\underline {\theta }=(\ldots ,\theta _{-n},\ldots ,\theta _{-1},\theta _{0})\in \Sigma ^{-}$
, let
$\underline {\theta }=(\ldots ,\theta _{-n},\ldots ,\theta _{-1},\theta _{0})\in \Sigma ^{-}$
, let
![]() $\underline {\theta }^n=(\theta _{-n},\ldots ,\theta _0)$
and define
$\underline {\theta }^n=(\theta _{-n},\ldots ,\theta _0)$
and define
![]() $k^{\underline {\theta }}_n:G(\theta _0)\to \mathbb {C}$
by
$k^{\underline {\theta }}_n:G(\theta _0)\to \mathbb {C}$
by
where
![]() $\phi _{\underline {\theta }^n}$
is the unique map in
$\phi _{\underline {\theta }^n}$
is the unique map in
![]() $Aff(\mathbb {C})=\{A(z)=az+b:a,b\in \mathbb {C},\,\,a\neq 0\}$
such that
$Aff(\mathbb {C})=\{A(z)=az+b:a,b\in \mathbb {C},\,\,a\neq 0\}$
such that
![]() $\phi _{\underline {\theta }^n}(c_{\underline {\theta }^n})=0$
,
$\phi _{\underline {\theta }^n}(c_{\underline {\theta }^n})=0$
,
![]() $D\phi _{\underline {\theta }^n}(c_{\underline {\theta }^n})e^{iv_{\underline {\theta }^n}}\in \mathbb {R}^+$
,
$D\phi _{\underline {\theta }^n}(c_{\underline {\theta }^n})e^{iv_{\underline {\theta }^n}}\in \mathbb {R}^+$
,
![]() $\mathrm {diam}(\phi _{\underline {\theta }^n}(G(\underline {\theta }^n)))=1$
. For the next theorem, we consider
$\mathrm {diam}(\phi _{\underline {\theta }^n}(G(\underline {\theta }^n)))=1$
. For the next theorem, we consider
![]() $k^{\underline {\theta }}_n$
extended to a small open neighborhood
$k^{\underline {\theta }}_n$
extended to a small open neighborhood
![]() $G^*(\theta _0)$
of
$G^*(\theta _0)$
of
![]() $G(\theta _0)$
(as in Lemma 2.1).
$G(\theta _0)$
(as in Lemma 2.1).
Theorem 2.1. Let K be a
![]() $C^m$
conformal Cantor set. For any
$C^m$
conformal Cantor set. For any
![]() $\underline {\theta }\in \Sigma ^-$
, the family of functions
$\underline {\theta }\in \Sigma ^-$
, the family of functions
![]() $k^{\underline {\theta }}_n:G^*(\theta _0)\to \mathbb {C}$
converges in the
$k^{\underline {\theta }}_n:G^*(\theta _0)\to \mathbb {C}$
converges in the
![]() $C^{[m]}$
topology, with an exponential rate of convergence independent of
$C^{[m]}$
topology, with an exponential rate of convergence independent of
![]() $\underline {\theta }$
, to a
$\underline {\theta }$
, to a
![]() $C^m$
function
$C^m$
function
![]() $k^{\underline {\theta }}:G^*(\theta _0)\to \mathbb {C}$
. The function
$k^{\underline {\theta }}:G^*(\theta _0)\to \mathbb {C}$
. The function
![]() $k^{\underline {\theta }}$
is a diffeomorphism onto its image and the derivative
$k^{\underline {\theta }}$
is a diffeomorphism onto its image and the derivative
![]() $Dk^{\underline {\theta }}(x)$
is conformal for all
$Dk^{\underline {\theta }}(x)$
is conformal for all
![]() $x\in K(\theta _0)$
.
$x\in K(\theta _0)$
.
Moreover, if
![]() $m\geq 2$
, then there is a constant
$m\geq 2$
, then there is a constant
![]() $C>0$
such that given
$C>0$
such that given
![]() $\underline {\theta }^1, \underline {\theta }^2 \in \Sigma ^-$
ending with the same letter,
$\underline {\theta }^1, \underline {\theta }^2 \in \Sigma ^-$
ending with the same letter,
The function
![]() $k^{\underline {\theta }}$
is called a limit geometry of K. Notice that the rate of convergence being independent of
$k^{\underline {\theta }}$
is called a limit geometry of K. Notice that the rate of convergence being independent of
![]() $\underline {\theta }$
implies that
$\underline {\theta }$
implies that
![]() $D^l k^{\underline {\theta }}$
, for
$D^l k^{\underline {\theta }}$
, for
![]() $0\leq l\leq [m]$
, depends continuously on
$0\leq l\leq [m]$
, depends continuously on
![]() $\underline {\theta }$
. The proof of Theorem 2.1 can also be found in [Reference Araújo and Moreira1].
$\underline {\theta }$
. The proof of Theorem 2.1 can also be found in [Reference Araújo and Moreira1].
For
![]() $\underline {\theta } \in \Sigma ^{-}$
,
$\underline {\theta } \in \Sigma ^{-}$
,
![]() $\underline {a}\in \Sigma ^\textit{fin}$
, such that
$\underline {a}\in \Sigma ^\textit{fin}$
, such that
![]() $\underline {a}$
starts with the last letter of
$\underline {a}$
starts with the last letter of
![]() $\underline {\theta }$
, define
$\underline {\theta }$
, define
 $$ \begin{align*} &G^{\underline{\theta}}(\underline{a})=k^{\underline{\theta}}(G(\underline{a})),\quad K^{\underline{\theta}}(\underline{a})=k^{\underline{\theta}}(K(\underline{a})),\quad c^{\underline{\theta}}_{\underline{a}}=k^{\underline{\theta}}(c_{\underline{a}})\\ &\text{exp} (iv^{\underline{\theta}}_{\underline{a}})=\frac{Dk^{\underline{\theta}}(c_{\underline{a}})}{\|Dk^{\underline{\theta}}(c_{\underline{a}})\|} \text{exp}(iv_{\underline{a}}),\quad r^{\underline{\theta}}_{\underline{a}}=\mathrm{diam}(G^{\underline{\theta}}(\underline{a})). \end{align*} $$
$$ \begin{align*} &G^{\underline{\theta}}(\underline{a})=k^{\underline{\theta}}(G(\underline{a})),\quad K^{\underline{\theta}}(\underline{a})=k^{\underline{\theta}}(K(\underline{a})),\quad c^{\underline{\theta}}_{\underline{a}}=k^{\underline{\theta}}(c_{\underline{a}})\\ &\text{exp} (iv^{\underline{\theta}}_{\underline{a}})=\frac{Dk^{\underline{\theta}}(c_{\underline{a}})}{\|Dk^{\underline{\theta}}(c_{\underline{a}})\|} \text{exp}(iv_{\underline{a}}),\quad r^{\underline{\theta}}_{\underline{a}}=\mathrm{diam}(G^{\underline{\theta}}(\underline{a})). \end{align*} $$
Let
![]() $F_{\underline {a}}^{\underline {\theta }}$
be the affine map determined by the equation
$F_{\underline {a}}^{\underline {\theta }}$
be the affine map determined by the equation
![]() $k^{\underline {\theta }}\circ f_{\underline {a}}=F_{\underline {a}}^{\underline {\theta }}\circ k^{\underline {\theta }\underline {a}}$
. It maps
$k^{\underline {\theta }}\circ f_{\underline {a}}=F_{\underline {a}}^{\underline {\theta }}\circ k^{\underline {\theta }\underline {a}}$
. It maps
![]() $0$
to
$0$
to
![]() $c_{\underline {a}}^{\underline {\theta }}$
and can be written using
$c_{\underline {a}}^{\underline {\theta }}$
and can be written using
![]() $r_{\underline {a}}^{\underline {\theta }}\in \mathbb {R}^+$
,
$r_{\underline {a}}^{\underline {\theta }}\in \mathbb {R}^+$
,
![]() $v_{\underline {a}}^{\underline {\theta }}\in \mathbb {R}/2\pi \mathbb {Z}$
as
$v_{\underline {a}}^{\underline {\theta }}\in \mathbb {R}/2\pi \mathbb {Z}$
as
Definition 2.1. We will say that a
![]() $C^m$
,
$C^m$
,
![]() $m\geq 2$
, Cantor set K is not essentially affine if there exist
$m\geq 2$
, Cantor set K is not essentially affine if there exist
![]() $\underline {\theta }^1,\underline {\theta }^2\in \Sigma ^{-}$
, ending in the same letter, and
$\underline {\theta }^1,\underline {\theta }^2\in \Sigma ^{-}$
, ending in the same letter, and
![]() $z_0\in K^{\underline {\theta }^2}(\theta ^2_0)$
such that
$z_0\in K^{\underline {\theta }^2}(\theta ^2_0)$
such that
![]() $D^2(k^{\underline {\theta }^1}\circ (k^{\underline {\theta }^2})^{-1})(z_0)\neq 0$
.
$D^2(k^{\underline {\theta }^1}\circ (k^{\underline {\theta }^2})^{-1})(z_0)\neq 0$
.
2.3 Mass distribution principle
Typically, estimating the Hausdorff dimension from below is harder than from above. One usual technique is the mass distribution principle that we state below.
Proposition 2.1. Let
![]() $F\subset \mathbb {R}^l$
be a Borel measurable set,
$F\subset \mathbb {R}^l$
be a Borel measurable set,
![]() $\nu $
a Borel measure with
$\nu $
a Borel measure with
![]() $\nu (F)>0$
, and
$\nu (F)>0$
, and
![]() $a,b>0$
,
$a,b>0$
,
![]() $s>0$
such that
$s>0$
such that
![]() $\nu (u)\leq a\cdot \mathrm {diam}(u)^s$
for all u measurable with
$\nu (u)\leq a\cdot \mathrm {diam}(u)^s$
for all u measurable with
![]() $\mathrm {diam}(u)<b$
. Then the Hausdorff dimension of F, denoted by
$\mathrm {diam}(u)<b$
. Then the Hausdorff dimension of F, denoted by
![]() $HD(F)$
, is bigger than s.
$HD(F)$
, is bigger than s.
The next proposition is a consequence of the mass distribution principle and it will be used to prove the desired dimension formula (Theorem B). Its proof is not difficult and can be found in [Reference Zamudio13, §1.3].
Let N be the node set of a rooted tree with the property that every node has finite index. Here, N can be described in the following way: there is a marked element
![]() $p_0\in N$
called the root of N; for each
$p_0\in N$
called the root of N; for each
![]() $p\in N$
, we have a finite set
$p\in N$
, we have a finite set
![]() $Ch(p)\subset N$
called the children of p; if
$Ch(p)\subset N$
called the children of p; if
![]() $p\neq q$
, then
$p\neq q$
, then
![]() $Ch(p)\cap Ch(q)=\emptyset $
; for any
$Ch(p)\cap Ch(q)=\emptyset $
; for any
![]() $q\in N$
, there is a sequence
$q\in N$
, there is a sequence
![]() $q_0,q_1,\ldots ,q_m$
such that
$q_0,q_1,\ldots ,q_m$
such that
![]() $q_0=p_0$
,
$q_0=p_0$
,
![]() $q_m=q$
, and
$q_m=q$
, and
![]() $q_{i+1}\in Ch(q_i)$
,
$q_{i+1}\in Ch(q_i)$
,
![]() $i=0,\ldots ,m-1$
, such q is called an m-level node of N. Denote by
$i=0,\ldots ,m-1$
, such q is called an m-level node of N. Denote by
![]() $I(k)$
the set of k-level nodes. Now N can be written as the disjoint union
$I(k)$
the set of k-level nodes. Now N can be written as the disjoint union
![]() $N=\sqcup _{k=0}^{\infty } I(k)$
.
$N=\sqcup _{k=0}^{\infty } I(k)$
.
Corollary 2.1. Suppose we have a set N as described above and assume that for each
![]() $p\in N$
, we have a Borel measurable set
$p\in N$
, we have a Borel measurable set
![]() $G(p)\subset \mathbb {R}^l$
with the following properties:
$G(p)\subset \mathbb {R}^l$
with the following properties:
-
(a) if
 $p\in Ch(q)$
, then
$p\in Ch(q)$
, then
 $\overline {G(p)}\subset G(q)$
;
$\overline {G(p)}\subset G(q)$
; -
(b) if
 $p_1,p_2\in Ch(q)$
,
$p_1,p_2\in Ch(q)$
,
 $p_1\neq p_2$
, then
$p_1\neq p_2$
, then
 $\overline {G(p_1)}\cap \overline {G(p_2)}=\emptyset $
;
$\overline {G(p_1)}\cap \overline {G(p_2)}=\emptyset $
; -
(c) the supremum
 $\sup \{ \mathrm {diam}(G(p)): p\in I(k)\}$
goes to zero as k goes to infinity;
$\sup \{ \mathrm {diam}(G(p)): p\in I(k)\}$
goes to zero as k goes to infinity; -
(d) there is a constant
 $\mu>1$
such that for any
$\mu>1$
such that for any
 $p\in Ch(q)$
, we have
$p\in Ch(q)$
, we have
 $\mathrm {diam}(G(p))\geq \mu ^{-1} \mathrm {diam}(G(q))$
;
$\mathrm {diam}(G(p))\geq \mu ^{-1} \mathrm {diam}(G(q))$
; -
(e) there is a constant
 $\mu>1$
such that for any
$\mu>1$
such that for any
 $p\in N$
, the set
$p\in N$
, the set
 $G(p)$
contains a ball of radius
$G(p)$
contains a ball of radius
 $\mu ^{-1}\mathrm {diam}(G(p))$
;
$\mu ^{-1}\mathrm {diam}(G(p))$
; -
(f) there is a number
 $s>0$
such that for any
$s>0$
such that for any
 $q\in N$
,
$q\in N$
,  $$ \begin{align*}\sum_{p\in Ch(q)} \mathrm{diam}(G(p))^s\geq \mathrm{diam}(G(q))^s.\end{align*} $$
$$ \begin{align*}\sum_{p\in Ch(q)} \mathrm{diam}(G(p))^s\geq \mathrm{diam}(G(q))^s.\end{align*} $$
Let F be the set
![]() $F=\bigcap _{k=0}^{\infty } \bigcup _{p\in I(k)} G(p)$
. Then
$F=\bigcap _{k=0}^{\infty } \bigcup _{p\in I(k)} G(p)$
. Then
![]() $HD(F)\geq s$
.
$HD(F)\geq s$
.
2.4 Not essentially real Cantor sets
In this subsection, we will present a hypothesis in the Cantor set that will guarantee it is indeed two dimensional. We remark that for regular Cantor sets in the real line, there is no analogous definition and results to those in this section. Those are objects that start appearing at dimension two.
Definition 2.2. We will say that a Cantor set K is essentially real if there exists
![]() $\underline {\theta }\in \Sigma ^-$
such that the limit Cantor set
$\underline {\theta }\in \Sigma ^-$
such that the limit Cantor set
![]() $K^{\underline {\theta }}(\theta _0)$
is contained in a straight line.
$K^{\underline {\theta }}(\theta _0)$
is contained in a straight line.
It is not difficult to prove that K is essentially real if and only if for every
![]() $\underline {\theta }\in \Sigma ^-$
, the limit Cantor set
$\underline {\theta }\in \Sigma ^-$
, the limit Cantor set
![]() $K^{\underline {\theta }}(\theta _0)$
is contained in a straight line. Moreover, one can prove that K being essentially real is equivalent to K being contained in a
$K^{\underline {\theta }}(\theta _0)$
is contained in a straight line. Moreover, one can prove that K being essentially real is equivalent to K being contained in a
![]() $C^1$
one-dimensional manifold embedded in the plane. For the proof of the scale recurrence lemma, we will suppose that the Cantor set is not essentially real, in such a case, one is able to control the quantity of elements
$C^1$
one-dimensional manifold embedded in the plane. For the proof of the scale recurrence lemma, we will suppose that the Cantor set is not essentially real, in such a case, one is able to control the quantity of elements
![]() $G^{\underline {\theta }}(\underline {a})$
close to an arbitrary line; this is the content of the next lemma.
$G^{\underline {\theta }}(\underline {a})$
close to an arbitrary line; this is the content of the next lemma.
Given
![]() $c>0,\rho >0$
, define
$c>0,\rho >0$
, define
![]() $\Sigma (c,\rho )=\{\underline {a}\in \Sigma ^\textit{fin}:\,\,c^{-1}\rho \leq \mathrm {diam}(G(\underline {a}))\leq c \rho \}$
. We can think of this as the set of
$\Sigma (c,\rho )=\{\underline {a}\in \Sigma ^\textit{fin}:\,\,c^{-1}\rho \leq \mathrm {diam}(G(\underline {a}))\leq c \rho \}$
. We can think of this as the set of
![]() $G(\underline {a})$
having approximate size
$G(\underline {a})$
having approximate size
![]() $\rho $
. Using standard techniques (see [Reference Palis and Takens10] or [Reference Zamudio13]), one can prove that there is a constant
$\rho $
. Using standard techniques (see [Reference Palis and Takens10] or [Reference Zamudio13]), one can prove that there is a constant
![]() $C>0$
, depending only on c and the Cantor set K and not depending on
$C>0$
, depending only on c and the Cantor set K and not depending on
![]() $\rho $
, such that
$\rho $
, such that
Suppose we have fixed a constant
![]() $C_5>0$
. Let
$C_5>0$
. Let
![]() $(a,b)\in B$
. A subset
$(a,b)\in B$
. A subset
![]() $D\subset \Sigma (C_5,\rho )$
is called a discretization of
$D\subset \Sigma (C_5,\rho )$
is called a discretization of
![]() $K(a,b)$
of order
$K(a,b)$
of order
![]() $\rho $
if
$\rho $
if
![]() $\bigcup _{\underline {a}\in D}K(\underline {a})=K(a,b)$
.
$\bigcup _{\underline {a}\in D}K(\underline {a})=K(a,b)$
.
Lemma 2.2. Let K be a Cantor set not essentially real. There exist an angle
![]() $\alpha \in (0,\pi /2)$
and numbers
$\alpha \in (0,\pi /2)$
and numbers
![]() $\rho _2>0$
,
$\rho _2>0$
,
![]() $a\in (0,1)$
, depending only on
$a\in (0,1)$
, depending only on
![]() $C_5$
and the Cantor set K, such that for any limit geometry
$C_5$
and the Cantor set K, such that for any limit geometry
![]() $k^{\underline {\theta }}$
,
$k^{\underline {\theta }}$
,
![]() $x\in G^{\underline {\theta }}(\theta _0)$
, line L,
$x\in G^{\underline {\theta }}(\theta _0)$
, line L,
![]() $s\in \mathbb {A}$
, D discretization of
$s\in \mathbb {A}$
, D discretization of
![]() $K(\theta _0, s)$
of order less than
$K(\theta _0, s)$
of order less than
![]() $\rho _2$
,
$\rho _2$
,
where
![]() $\mathrm {Cone}(x,L,\alpha )$
is the set of
$\mathrm {Cone}(x,L,\alpha )$
is the set of
![]() $z\in \mathbb {C}$
such that the vector
$z\in \mathbb {C}$
such that the vector
![]() $z-x$
forms an angle of measure less than
$z-x$
forms an angle of measure less than
![]() $\alpha $
with the line L.
$\alpha $
with the line L.
Another use of the not essentially real hypothesis will be given in the next lemma. Let K be a Cantor set, for
![]() $x \in K$
, consider the set
$x \in K$
, consider the set
 $$ \begin{align*}K^{dir}_x :=\bigcap_{\delta>0} \overline{\bigg\{\frac{y-x}{|y-x|}:y\in B_{\delta}(x)\cap (K\setminus \{x\})\bigg\}},\end{align*} $$
$$ \begin{align*}K^{dir}_x :=\bigcap_{\delta>0} \overline{\bigg\{\frac{y-x}{|y-x|}:y\in B_{\delta}(x)\cap (K\setminus \{x\})\bigg\}},\end{align*} $$
where
![]() $B_{\delta }(x)$
is the open ball of radius
$B_{\delta }(x)$
is the open ball of radius
![]() $\delta $
centered at x. If K is not essentially real, then the set
$\delta $
centered at x. If K is not essentially real, then the set
![]() $K^{dir}_x$
has two linearly independent vectors (over
$K^{dir}_x$
has two linearly independent vectors (over
![]() $\mathbb {R}$
) and then the following lemma holds for K.
$\mathbb {R}$
) and then the following lemma holds for K.
Lemma 2.3. Let K be a Cantor set and f a
![]() $C^l$
function from a neighborhood of K into
$C^l$
function from a neighborhood of K into
![]() $\mathbb {R}^2$
. Suppose that f is conformal at K, that is,
$\mathbb {R}^2$
. Suppose that f is conformal at K, that is,
![]() $Df(x)$
is conformal for all
$Df(x)$
is conformal for all
![]() $x\in K$
, and
$x\in K$
, and
![]() $K^{dir}_x$
has two linearly independent vectors (over
$K^{dir}_x$
has two linearly independent vectors (over
![]() $\mathbb {R}$
) for all
$\mathbb {R}$
) for all
![]() $x\in K$
. Then, for all
$x\in K$
. Then, for all
![]() $x\in K$
, the l-linear map
$x\in K$
, the l-linear map
![]() $D^l f(x):\mathbb {R}^2\times \cdots \times \mathbb {R}^2 \to \mathbb {R}^2$
is conformal, that is, there is a complex number
$D^l f(x):\mathbb {R}^2\times \cdots \times \mathbb {R}^2 \to \mathbb {R}^2$
is conformal, that is, there is a complex number
![]() $c^l_x$
such that
$c^l_x$
such that
The operation
![]() $\cdot $
on the right-hand side of the last equality corresponds to complex multiplication.
$\cdot $
on the right-hand side of the last equality corresponds to complex multiplication.
In particular, if a Cantor set is not essentially real and not essentially affine, then for the values
![]() $z_0 \in K$
,
$z_0 \in K$
,
![]() $\underline {\theta }^1,\underline {\theta }^2\in \Sigma ^{-}$
, given by Definition 2.1, there is a non-zero complex number
$\underline {\theta }^1,\underline {\theta }^2\in \Sigma ^{-}$
, given by Definition 2.1, there is a non-zero complex number
![]() $d_0$
such that
$d_0$
such that
2.5 Renormalization operator
From now on, we will be working with a finite set of conformal regular Cantor sets
![]() $K_1,\ldots ,K_n$
. To each of them, we have various objects associated, as defined in the previous subsections. We will use subscripts and superscripts to differentiate the objects from one Cantor set to the other. For example, we use
$K_1,\ldots ,K_n$
. To each of them, we have various objects associated, as defined in the previous subsections. We will use subscripts and superscripts to differentiate the objects from one Cantor set to the other. For example, we use
![]() $\Sigma _j(c,\rho )$
for the set
$\Sigma _j(c,\rho )$
for the set
![]() $\Sigma (c,\rho )$
, which was defined in the last subsection, associated to the Cantor set
$\Sigma (c,\rho )$
, which was defined in the last subsection, associated to the Cantor set
![]() $K_j$
. We will denote by
$K_j$
. We will denote by
![]() $d_j$
the Hausdorff dimension of the Cantor set
$d_j$
the Hausdorff dimension of the Cantor set
![]() $K_j$
. In this section, we will define renormalization operators, which are operators associated to the family
$K_j$
. In this section, we will define renormalization operators, which are operators associated to the family
![]() $K_1,\ldots ,K_n$
of Cantor sets.
$K_1,\ldots ,K_n$
of Cantor sets.
Define
![]() $J=\mathbb {R}^{n-1}\times \mathbb {T}^n$
, where
$J=\mathbb {R}^{n-1}\times \mathbb {T}^n$
, where
![]() $\mathbb {T}=\mathbb {R}/(2\pi \mathbb {Z})$
. The group
$\mathbb {T}=\mathbb {R}/(2\pi \mathbb {Z})$
. The group
![]() $\mathbb {T}$
is endowed with the unique invariant distance giving diameter
$\mathbb {T}$
is endowed with the unique invariant distance giving diameter
![]() $2\pi $
to the whole space. For
$2\pi $
to the whole space. For
![]() $v\in \mathbb {T}$
, we denote by
$v\in \mathbb {T}$
, we denote by
![]() $\|v\|$
the distance between v and the zero element. The space J is an abelian locally compact group. We put on J the unique invariant metric such that the distance between
$\|v\|$
the distance between v and the zero element. The space J is an abelian locally compact group. We put on J the unique invariant metric such that the distance between
![]() $(t_1,\ldots ,t_{n-1},v_1,\ldots ,v_n)$
and the zero element is
$(t_1,\ldots ,t_{n-1},v_1,\ldots ,v_n)$
and the zero element is
![]() $\max _j\{|t_j|,\|v_j\|\}$
.
$\max _j\{|t_j|,\|v_j\|\}$
.
Lemma 3.1 justifies why we choose to work on
![]() $J=\mathbb {R}^{n-1}\times \mathbb {T}^n$
. The lemma states that the ‘renormalization’ of h, given by
$J=\mathbb {R}^{n-1}\times \mathbb {T}^n$
. The lemma states that the ‘renormalization’ of h, given by
![]() $h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
, becomes, modulo composition by an affine function, arbitrarily close to a function of the form
$h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
, becomes, modulo composition by an affine function, arbitrarily close to a function of the form
![]() $B\circ A(t,v)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
. The pair
$B\circ A(t,v)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
. The pair
![]() $(t,v)$
, parameterizing the maps
$(t,v)$
, parameterizing the maps
![]() $A(\cdot ,\cdot )$
, is in
$A(\cdot ,\cdot )$
, is in
![]() $\mathbb {R}^{n-1}\times \mathbb {T}^n$
. In fact, if the function h were not only
$\mathbb {R}^{n-1}\times \mathbb {T}^n$
. In fact, if the function h were not only
![]() $C^1$
but holomorphic, then we could reduce further the type of function A appearing and take J as
$C^1$
but holomorphic, then we could reduce further the type of function A appearing and take J as
![]() $\mathbb {R}^{n-1}\times \mathbb {T}^{n-1}$
. The renormalization operators are then defined observing how the expression
$\mathbb {R}^{n-1}\times \mathbb {T}^{n-1}$
. The renormalization operators are then defined observing how the expression
![]() $A(t,v)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
changes when one composes it by
$A(t,v)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
changes when one composes it by
![]() $(f_{\underline {b}^1},\ldots ,f_{\underline {b}^n})$
.
$(f_{\underline {b}^1},\ldots ,f_{\underline {b}^n})$
.
For
![]() $(\underline {b}^1,\ldots ,\underline {b}^n)\in \Sigma ^\textit{fin}_1\times \cdots \times \Sigma ^\textit{fin}_n$
, define the operator
$(\underline {b}^1,\ldots ,\underline {b}^n)\in \Sigma ^\textit{fin}_1\times \cdots \times \Sigma ^\textit{fin}_n$
, define the operator
given by
 $$ \begin{align*} &T_{\underline{b}^1,\ldots,\underline{b}^n}(\underline{\theta}^1,\ldots,\underline{\theta}^n,t_1,\ldots,t_{n-1},v_1,\ldots,v_n)\\ &\quad=\bigg(\underline{\theta}^1\underline{b}^1,\ldots,\underline{\theta}^n\underline{b}^n,t_1+\log \frac{r_{\underline{b}^1}^{\underline{\theta}^1}}{r_{\underline{b}^n}^{\underline{\theta}^n}},\ldots,t_{n-1}+\log \frac{r_{\underline{b}^{n-1}}^{\underline{\theta}^{n-1}}}{r_{\underline{b}^n}^{\underline{\theta}^n}},v_1+v_{\underline{b}^1}^{\underline{\theta}^1},\ldots,v_n+v_{\underline{b}^n}^{\underline{\theta}^n}\bigg). \end{align*} $$
$$ \begin{align*} &T_{\underline{b}^1,\ldots,\underline{b}^n}(\underline{\theta}^1,\ldots,\underline{\theta}^n,t_1,\ldots,t_{n-1},v_1,\ldots,v_n)\\ &\quad=\bigg(\underline{\theta}^1\underline{b}^1,\ldots,\underline{\theta}^n\underline{b}^n,t_1+\log \frac{r_{\underline{b}^1}^{\underline{\theta}^1}}{r_{\underline{b}^n}^{\underline{\theta}^n}},\ldots,t_{n-1}+\log \frac{r_{\underline{b}^{n-1}}^{\underline{\theta}^{n-1}}}{r_{\underline{b}^n}^{\underline{\theta}^n}},v_1+v_{\underline{b}^1}^{\underline{\theta}^1},\ldots,v_n+v_{\underline{b}^n}^{\underline{\theta}^n}\bigg). \end{align*} $$
These are called renormalization operators. They will appear in the statement of the scale recurrence lemma. For
![]() $r>0$
, we also define the set
$r>0$
, we also define the set
and denote by
![]() $\nu $
the Haar measure on J giving measure
$\nu $
the Haar measure on J giving measure
![]() $(2\pi )^n$
to the set
$(2\pi )^n$
to the set
![]() $J_{1/2}$
.
$J_{1/2}$
.
2.6 Scale recurrence lemma
In this subsection, we state one of the principal results in the paper. This is a multidimensional conformal version of the scale recurrence lemma of Moreira and Yoccoz [Reference Moreira and Yoccoz7]. The proof is technical and will be left for the end of the paper.
Theorem A. (Scale recurrence lemma)
Let
![]() $K_1$
,
$K_1$
,
![]() $K_2,\ldots ,K_{n}$
be
$K_2,\ldots ,K_{n}$
be
![]() $C^m$
conformal regular Cantor sets with
$C^m$
conformal regular Cantor sets with
![]() $m\geq 2$
. Suppose they are not essentially affine and not essentially real. Denote by
$m\geq 2$
. Suppose they are not essentially affine and not essentially real. Denote by
![]() $d_j$
the Hausdorff dimension of
$d_j$
the Hausdorff dimension of
![]() $K_j$
,
$K_j$
,
![]() $1\leq j\leq n$
. If
$1\leq j\leq n$
. If
![]() $r,c_0$
are conveniently large, there exist
$r,c_0$
are conveniently large, there exist
![]() $c_1,c_2,c_3,\rho _0>0$
with the following properties: given
$c_1,c_2,c_3,\rho _0>0$
with the following properties: given
![]() $0<\rho <\rho _0$
, and a family
$0<\rho <\rho _0$
, and a family
![]() $F(\underline {a}^1,\ldots ,\underline {a}^n)$
of subsets of
$F(\underline {a}^1,\ldots ,\underline {a}^n)$
of subsets of
![]() $J_r$
,
$J_r$
,
![]() $(\underline {a}^1,\ldots ,\underline {a}^n)\in \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
, such that
$(\underline {a}^1,\ldots ,\underline {a}^n)\in \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
, such that
there is another family
![]() $F^*(\underline {a}^1,\ldots ,\underline {a}^n)$
of subsets of
$F^*(\underline {a}^1,\ldots ,\underline {a}^n)$
of subsets of
![]() $J_r$
satisfying the following properties.
$J_r$
satisfying the following properties.
-
(i) For any
 $(\underline {a}^1,\ldots ,\underline {a}^n)$
,
$(\underline {a}^1,\ldots ,\underline {a}^n)$
,
 $F^*(\underline {a}^1,\ldots ,\underline {a}^n)$
is contained in the
$F^*(\underline {a}^1,\ldots ,\underline {a}^n)$
is contained in the
 $c_2 \rho $
-neighborhood of
$c_2 \rho $
-neighborhood of
 $F(\underline {a}^1,\ldots ,\underline {a}^n)$
.
$F(\underline {a}^1,\ldots ,\underline {a}^n)$
. -
(ii) Let
 $(\underline {a}^1,\ldots ,\underline {a}^n)\in \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
,
$(\underline {a}^1,\ldots ,\underline {a}^n)\in \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
,
 $(t,v)\in F^*(\underline {a}^1,\ldots ,\underline {a}^n)$
; there exist at least
$(t,v)\in F^*(\underline {a}^1,\ldots ,\underline {a}^n)$
; there exist at least
 $c_3\rho ^{-(d_1+d_2+\cdots +d_n)}$
tuples
$c_3\rho ^{-(d_1+d_2+\cdots +d_n)}$
tuples
 $(\underline {b}^1,\ldots ,\underline {b}^n)\in \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
(with
$(\underline {b}^1,\ldots ,\underline {b}^n)\in \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
(with
 $\underline {b}^1,\ldots ,\underline {b}^n$
starting with the last letter of
$\underline {b}^1,\ldots ,\underline {b}^n$
starting with the last letter of
 $\underline {a}^1,\ldots ,\underline {a}^n$
) such that, if
$\underline {a}^1,\ldots ,\underline {a}^n$
) such that, if
 $\underline {\theta }^i \in \Sigma _i^{-}$
ends with
$\underline {\theta }^i \in \Sigma _i^{-}$
ends with
 $\underline {a}^i$
,
$\underline {a}^i$
,
 $i=1,\ldots,n$
, and the
$i=1,\ldots,n$
, and the $$ \begin{align*}T_{\underline{b}^1,\ldots,\underline{b}^n}(\underline{\theta}^1,\ldots,\underline{\theta}^n,t,v)=(\underline{\theta}^1\underline{b}^1,\ldots,\underline{\theta}^n\underline{b}^n,\tilde{t},\tilde{v}),\end{align*} $$
$$ \begin{align*}T_{\underline{b}^1,\ldots,\underline{b}^n}(\underline{\theta}^1,\ldots,\underline{\theta}^n,t,v)=(\underline{\theta}^1\underline{b}^1,\ldots,\underline{\theta}^n\underline{b}^n,\tilde{t},\tilde{v}),\end{align*} $$
 $\rho $
-neighborhood of
$\rho $
-neighborhood of
 $(\tilde {t},\tilde {v})\in J$
is contained in
$(\tilde {t},\tilde {v})\in J$
is contained in
 $F^*(\underline {b}^1,\ldots ,\underline {b}^n)$
.
$F^*(\underline {b}^1,\ldots ,\underline {b}^n)$
.
-
(iii)
 $\nu (F^*(\underline {a}^1,\ldots ,\underline {a}^n))\geq \nu (J_r)/2$
for at least half of the
$\nu (F^*(\underline {a}^1,\ldots ,\underline {a}^n))\geq \nu (J_r)/2$
for at least half of the
 $(\underline {a}^1,\ldots ,\underline {a}^n)\in \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
.
$(\underline {a}^1,\ldots ,\underline {a}^n)\in \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
.
3 Dimension formula
In this section, we will prove the dimension formula (Theorem B), which is one of the main theorems in the paper. First, we will introduce some notation. Second, we will present the discrete Marstrand property, which will be an important tool. Finally, we give the proof of Theorem B.
The idea of the proof of Theorem B is to use the mass distribution principle in the form of Corollary 2.1. The role of the sets
![]() $G(p)$
will be played by sets of the form
$G(p)$
will be played by sets of the form
![]() $h(G(\underline {a}^1)\times \cdots \times G(\underline {a}^n))$
. Thus, we will estimate the Hausdorff dimension of a subset of
$h(G(\underline {a}^1)\times \cdots \times G(\underline {a}^n))$
. Thus, we will estimate the Hausdorff dimension of a subset of
![]() $h(K_1\times \cdots \times K_n)$
by defining a nested sequence of sets of the form
$h(K_1\times \cdots \times K_n)$
by defining a nested sequence of sets of the form
![]() $h(G(\underline {a}^1)\times \cdots \times G(\underline {a}^n))$
verifying the properties in the corollary. The main difficulty with this type of argument is to guarantee property (f). Roughly speaking, we use the Marstrand property to guarantee that for every size
$h(G(\underline {a}^1)\times \cdots \times G(\underline {a}^n))$
verifying the properties in the corollary. The main difficulty with this type of argument is to guarantee property (f). Roughly speaking, we use the Marstrand property to guarantee that for every size
![]() $\rho $
, we have a ‘positive’ proportion of sets
$\rho $
, we have a ‘positive’ proportion of sets
![]() $G(\underline {a}^1)\times \cdots \times G(\underline {a}^n)$
, with
$G(\underline {a}^1)\times \cdots \times G(\underline {a}^n)$
, with
![]() $\underline {a}^j\in \Sigma _j(c_0,\rho )$
, such that their images by h are disjoint. This helps us get property (f) at a certain level. To be able to iterate this argument and to have property (f) at all levels, one uses the scale recurrence lemma.
$\underline {a}^j\in \Sigma _j(c_0,\rho )$
, such that their images by h are disjoint. This helps us get property (f) at a certain level. To be able to iterate this argument and to have property (f) at all levels, one uses the scale recurrence lemma.
We will use the notation
![]() $R(\rho )= \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
, and think of any element
$R(\rho )= \Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
, and think of any element
![]() $Q=(\underline {a}^1,\ldots ,\underline {a}^n)\in R(\rho )$
as the set
$Q=(\underline {a}^1,\ldots ,\underline {a}^n)\in R(\rho )$
as the set
![]() $G(\underline {a}^1)\times \cdots \times G(\underline {a}^n)$
. Given a function
$G(\underline {a}^1)\times \cdots \times G(\underline {a}^n)$
. Given a function
![]() $\varphi $
defined on a neighborhood of
$\varphi $
defined on a neighborhood of
![]() $G(\underline {a}^1)\times \cdots \times G(\underline {a}^n)$
, we write
$G(\underline {a}^1)\times \cdots \times G(\underline {a}^n)$
, we write
![]() $\varphi (Q)$
to denote the set
$\varphi (Q)$
to denote the set
![]() $\varphi (G(\underline {a}^1)\times \cdots \times G(\underline {a}^n))$
.
$\varphi (G(\underline {a}^1)\times \cdots \times G(\underline {a}^n))$
.
To each
![]() $(t,v)\in J$
, we associate the linear map
$(t,v)\in J$
, we associate the linear map
![]() $A(t,v):\mathbb {C}^n\to \mathbb {C}^n$
,
$A(t,v):\mathbb {C}^n\to \mathbb {C}^n$
,
We consider the composition
![]() $\pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,t,v}:= A(t,v)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
; these maps are related to the renormalization operators by the following equation:
$\pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,t,v}:= A(t,v)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
; these maps are related to the renormalization operators by the following equation:
where
![]() $B:\mathbb {C}^n\to \mathbb {C}^n$
is an affine function of the form
$B:\mathbb {C}^n\to \mathbb {C}^n$
is an affine function of the form
![]() $B(z)=\alpha \cdot z + \beta $
for
$B(z)=\alpha \cdot z + \beta $
for
![]() $\alpha \in \mathbb {R}$
. In fact, this equation is the reason why we defined the renormalization operators as we did.
$\alpha \in \mathbb {R}$
. In fact, this equation is the reason why we defined the renormalization operators as we did.
One of the main reasons to use limit geometries is that they appear naturally when one considers compositions of a
![]() $C^1$
function with the maps
$C^1$
function with the maps
![]() $f_{\underline {a}}$
. This is explained in the next lemma.
$f_{\underline {a}}$
. This is explained in the next lemma.
Lemma 3.1. Let h be a
![]() $C^1$
function defined from a neighborhood of
$C^1$
function defined from a neighborhood of
![]() $K_1\times \cdots \times K_n$
into
$K_1\times \cdots \times K_n$
into
![]() $\mathbb {R}^l$
, and
$\mathbb {R}^l$
, and
![]() $r>0$
. There exists a function
$r>0$
. There exists a function
![]() $E:(0,\infty )\to \mathbb {R}$
, depending only on h, r, and the Cantor sets, such that
$E:(0,\infty )\to \mathbb {R}$
, depending only on h, r, and the Cantor sets, such that
![]() $\lim _{t\to 0}E(t)=0$
and with the following property: for any
$\lim _{t\to 0}E(t)=0$
and with the following property: for any
![]() $(\underline {a}^1,\ldots ,\underline {a}^n)$
such that
$(\underline {a}^1,\ldots ,\underline {a}^n)$
such that
consider the affine function
![]() $L:\mathbb {R}^{l}\to \mathbb {R}^{l}$
given by
$L:\mathbb {R}^{l}\to \mathbb {R}^{l}$
given by
![]() $L(z)={1}/{r_{\underline {a}^n}}(z-h(c_{\underline {a}^1},\ldots ,c_{\underline {a}^n}))$
. Then for any
$L(z)={1}/{r_{\underline {a}^n}}(z-h(c_{\underline {a}^1},\ldots ,c_{\underline {a}^n}))$
. Then for any
![]() $\underline {\theta }^1,\ldots ,\underline {\theta }^n$
ending in
$\underline {\theta }^1,\ldots ,\underline {\theta }^n$
ending in
![]() $\underline {a}^1,\ldots ,\underline {a}^n$
, the supremum distance between
$\underline {a}^1,\ldots ,\underline {a}^n$
, the supremum distance between
![]() $L\circ h \circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
and
$L\circ h \circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
and
![]() $Dh(c_{\underline {a}^1},\ldots ,c_{\underline {a}^n})\circ A(s)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
is less than
$Dh(c_{\underline {a}^1},\ldots ,c_{\underline {a}^n})\circ A(s)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
is less than
![]() $E(\max _{1\leq j\leq n} r_{\underline {a}^j})$
.
$E(\max _{1\leq j\leq n} r_{\underline {a}^j})$
.
This lemma is saying that
![]() $h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
, modulo composition by an affine function on the left, becomes arbitrarily close to a function of the form
$h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
, modulo composition by an affine function on the left, becomes arbitrarily close to a function of the form
![]() $B\circ A(t,v)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
as the length of the words
$B\circ A(t,v)\circ (k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
as the length of the words
![]() $\underline {a}^j$
increases.
$\underline {a}^j$
increases.
Proof. Write
![]() $h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
as
$h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
as
Use the fact that
![]() $(\phi _{\underline {a}^1}\circ f_{\underline {a}^1},\ldots ,\phi _{\underline {a}^n}\circ f_{\underline {a}^n})$
becomes close to a limit geometry
$(\phi _{\underline {a}^1}\circ f_{\underline {a}^1},\ldots ,\phi _{\underline {a}^n}\circ f_{\underline {a}^n})$
becomes close to a limit geometry
![]() $(k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
and Taylor first-order approximation for
$(k^{\underline {\theta }^1},\ldots ,k^{\underline {\theta }^n})$
and Taylor first-order approximation for
![]() $h\circ (\phi _{\underline {a}^1}^{-1},\ldots ,\phi _{\underline {a}^n}^{-1})$
.
$h\circ (\phi _{\underline {a}^1}^{-1},\ldots ,\phi _{\underline {a}^n}^{-1})$
.
3.1 Discrete Marstrand property
In this section, we present and prove the discrete Marstrand property. We first state two linear algebra results that we will need.
Lemma 3.2. Let
![]() $A:\mathbb {R}^n\to \mathbb {R}^d$
be a linear map,
$A:\mathbb {R}^n\to \mathbb {R}^d$
be a linear map,
![]() $A\neq 0$
, and denote by
$A\neq 0$
, and denote by
![]() $\sigma $
the smallest non-zero singular value of A. Then
$\sigma $
the smallest non-zero singular value of A. Then
![]() $\mathrm {dist}(x,\mathrm {ker}(A))\leq {|Ax|}/{\sigma }$
for all
$\mathrm {dist}(x,\mathrm {ker}(A))\leq {|Ax|}/{\sigma }$
for all
![]() $x\in \mathbb {R}^n$
.
$x\in \mathbb {R}^n$
.
Lemma 3.3. Let
![]() $E_1,E_2 \subset \mathbb {R}^n$
be linear subspaces such that
$E_1,E_2 \subset \mathbb {R}^n$
be linear subspaces such that
![]() $E_1+E_2=\mathbb {R}^n$
. Denote by
$E_1+E_2=\mathbb {R}^n$
. Denote by
![]() $\theta $
the angle between
$\theta $
the angle between
![]() $E_1$
and
$E_1$
and
![]() $E_2$
. Define
$E_2$
. Define
![]() $I=E_1\cap E_2$
,
$I=E_1\cap E_2$
,
![]() $L_1=I^{\perp }\cap E_1$
, and
$L_1=I^{\perp }\cap E_1$
, and
![]() $L_2=I^{\perp }\cap E_2$
. For
$L_2=I^{\perp }\cap E_2$
. For
![]() $x=l_1+v+l_2$
, with
$x=l_1+v+l_2$
, with
![]() $l_1\in L_1$
,
$l_1\in L_1$
,
![]() $l_2\in L_2$
,
$l_2\in L_2$
,
![]() $v\in I$
, we have
$v\in I$
, we have
The next proposition is the main tool that will allow us to obtain the discrete Marstrand property. Given an
![]() $\mathbb {R}$
-linear map
$\mathbb {R}$
-linear map
![]() $B: \mathbb {C}^n\to \mathbb {R}^l$
, we will say it satisfies the transversality condition if for any set
$B: \mathbb {C}^n\to \mathbb {R}^l$
, we will say it satisfies the transversality condition if for any set
![]() $A\subset \{1,\ldots ,n\}$
, we have
$A\subset \{1,\ldots ,n\}$
, we have
![]() $\textrm {dim}(Im(B|_{\{z_j=0:j\notin A\}}))=\min \{l,2\cdot \# A\};$
in all this subsection, B will denote one such map.
$\textrm {dim}(Im(B|_{\{z_j=0:j\notin A\}}))=\min \{l,2\cdot \# A\};$
in all this subsection, B will denote one such map.
Proposition 3.1. Let
![]() $r>0$
and
$r>0$
and
![]() $B:\mathbb {C}^n\to \mathbb {R}^l$
a linear map satisfying the transversality condition. There exists a constant C, depending only on r and B, such that for any pair of subsets
$B:\mathbb {C}^n\to \mathbb {R}^l$
a linear map satisfying the transversality condition. There exists a constant C, depending only on r and B, such that for any pair of subsets
![]() $Q_1,Q_2 \subset \mathbb {C}^n$
, we have
$Q_1,Q_2 \subset \mathbb {C}^n$
, we have
 $$ \begin{align*}\nu(\{s\in J_r: B\circ A(s)(Q_1) \cap B\circ A(s)(Q_2)\neq \emptyset\})\leq C \bigg(\frac{\max \{\mathrm{diam}(Q_1),\mathrm{diam}(Q_2)\}}{\mathrm{dist}(Q_1,Q_2)}\bigg)^l\!,\end{align*} $$
$$ \begin{align*}\nu(\{s\in J_r: B\circ A(s)(Q_1) \cap B\circ A(s)(Q_2)\neq \emptyset\})\leq C \bigg(\frac{\max \{\mathrm{diam}(Q_1),\mathrm{diam}(Q_2)\}}{\mathrm{dist}(Q_1,Q_2)}\bigg)^l\!,\end{align*} $$
where
![]() $\mathrm {dist}(Q_1,Q_2)$
denotes the distance between
$\mathrm {dist}(Q_1,Q_2)$
denotes the distance between
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
.
$Q_2$
.
Proof. Throughout the proof, we will use the notation
![]() $P=O(Q)$
, meaning that there is a constant
$P=O(Q)$
, meaning that there is a constant
![]() $\tilde {C}$
, depending only on r and B, such that
$\tilde {C}$
, depending only on r and B, such that
![]() $P\leq \tilde {C} \cdot Q$
.
$P\leq \tilde {C} \cdot Q$
.
Given a subset
![]() $A\subset \{1,2,\ldots ,n\}$
, we consider the subspace
$A\subset \{1,2,\ldots ,n\}$
, we consider the subspace
![]() $\mathbb {C}^A=\{(z_1,\ldots ,z_n)\in \mathbb {C}^n: z_j=0\,\text { for all } j\notin A\}.$
By the transversality condition, we can choose
$\mathbb {C}^A=\{(z_1,\ldots ,z_n)\in \mathbb {C}^n: z_j=0\,\text { for all } j\notin A\}.$
By the transversality condition, we can choose
![]() $\theta>0$
, only depending on B, such that the angle between
$\theta>0$
, only depending on B, such that the angle between
![]() $\mathrm {ker}(B)$
and
$\mathrm {ker}(B)$
and
![]() $\mathbb {C}^A$
is bigger than
$\mathbb {C}^A$
is bigger than
![]() $\theta $
for any non-empty subset A.
$\theta $
for any non-empty subset A.
Denote
![]() $\max \{\mathrm {diam}(Q_1),\mathrm {diam}(Q_2)\}$
by
$\max \{\mathrm {diam}(Q_1),\mathrm {diam}(Q_2)\}$
by
![]() $\rho $
. Fix
$\rho $
. Fix
![]() $c_1,c_2 \in \mathbb {C}^n$
such that
$c_1,c_2 \in \mathbb {C}^n$
such that
and
![]() $c_2-c_1$
has all its coordinates in
$c_2-c_1$
has all its coordinates in
![]() $\mathbb {C}^n$
different from zero. Suppose that
$\mathbb {C}^n$
different from zero. Suppose that
![]() $s\in J_r$
is such that
$s\in J_r$
is such that
![]() $BA(s)(Q_1) \cap BA(s)(Q_2)\neq \emptyset .$
Then there are
$BA(s)(Q_1) \cap BA(s)(Q_2)\neq \emptyset .$
Then there are
![]() $\tilde {c}_1\in Q_1$
,
$\tilde {c}_1\in Q_1$
,
![]() $\tilde {c}_2\in Q_2$
verifying
$\tilde {c}_2\in Q_2$
verifying
![]() $B\circ A(s)(\tilde {c}_1)=B\circ A(s)(\tilde {c}_2)$
. We conclude that
$B\circ A(s)(\tilde {c}_1)=B\circ A(s)(\tilde {c}_2)$
. We conclude that
Define
![]() $x=({c_2-c_1})/{|c_2-c_1|}$
, and hence
$x=({c_2-c_1})/{|c_2-c_1|}$
, and hence
![]() $|B\circ A(s)(x)|=O({\rho }/{\mathrm {dist}(Q_1,Q_2)}).$
By the first linear algebra lemma, we get that
$|B\circ A(s)(x)|=O({\rho }/{\mathrm {dist}(Q_1,Q_2)}).$
By the first linear algebra lemma, we get that
![]() $\mathrm {dist}(A(s)(x), \mathrm {ker}(B))=O({\rho }/{\mathrm {dist}(Q_1,Q_2)}).$
Up until now, we have proven that there is a constant
$\mathrm {dist}(A(s)(x), \mathrm {ker}(B))=O({\rho }/{\mathrm {dist}(Q_1,Q_2)}).$
Up until now, we have proven that there is a constant
![]() $C_1$
, depending only on r and B, such that
$C_1$
, depending only on r and B, such that
Notice that if
![]() ${\rho }/{\mathrm {dist}(Q_1,Q_2)} \geq ({e^{-r} \sin \theta })/{4 C_1},$
then the proposition follows taking
${\rho }/{\mathrm {dist}(Q_1,Q_2)} \geq ({e^{-r} \sin \theta })/{4 C_1},$
then the proposition follows taking
![]() $C =(2r)^{n-1} (2\pi )^n ({4C_1}/{e^{-r} \sin \theta })^{l}$
. This is thanks to the fact that
$C =(2r)^{n-1} (2\pi )^n ({4C_1}/{e^{-r} \sin \theta })^{l}$
. This is thanks to the fact that
For the rest of the proof, we suppose
![]() ${\rho }/{\mathrm {dist}(Q_1,Q_2)} < ({e^{-r} \sin \theta })/{4 C_1}$
. Define
${\rho }/{\mathrm {dist}(Q_1,Q_2)} < ({e^{-r} \sin \theta })/{4 C_1}$
. Define
![]() $a=({e^{-r} \sin \theta })/{4n}$
and write
$a=({e^{-r} \sin \theta })/{4n}$
and write
![]() $x\in \mathbb {C}^n$
as
$x\in \mathbb {C}^n$
as
![]() $x=(e^{\chi _1+i\phi _1},\ldots ,e^{\chi _n+i\phi _n}).$
Consider the set
$x=(e^{\chi _1+i\phi _1},\ldots ,e^{\chi _n+i\phi _n}).$
Consider the set
and the subspace
![]() $\mathbb {C}^A$
; we will see that
$\mathbb {C}^A$
; we will see that
![]() $\textrm {dim}_{\mathbb {R}}\mathbb {C}^A\geq l$
. Let
$\textrm {dim}_{\mathbb {R}}\mathbb {C}^A\geq l$
. Let
![]() $u\in \mathbb {C}^A$
be the orthogonal projection of
$u\in \mathbb {C}^A$
be the orthogonal projection of
![]() $A(s)(x)$
in
$A(s)(x)$
in
![]() $\mathbb {C}^A$
. By the definition of
$\mathbb {C}^A$
. By the definition of
![]() $\mathbb {C}^A$
, we have
$\mathbb {C}^A$
, we have
![]() $|A(s)x-u|< na$
. Given that
$|A(s)x-u|< na$
. Given that
![]() $\|A(s)\|\geq e^{-r}$
(remember that
$\|A(s)\|\geq e^{-r}$
(remember that
![]() $s\in J_r$
) and
$s\in J_r$
) and
![]() $na<e^{-r}/2$
, we have
$na<e^{-r}/2$
, we have
If
![]() $\textrm {dim}_{\mathbb {R}} \mathbb {C}^A<l$
, the transversality implies
$\textrm {dim}_{\mathbb {R}} \mathbb {C}^A<l$
, the transversality implies
![]() $\mathbb {C}^A \cap \mathrm {ker}(B)=\{0\}$
and then, by the choice of
$\mathbb {C}^A \cap \mathrm {ker}(B)=\{0\}$
and then, by the choice of
![]() $\theta $
, we would get
$\theta $
, we would get
![]() $\mathrm {dist}(u,\mathrm {ker}(B))\geq |u|\sin \theta \geq ({e^{-r}\sin \theta })/{2}.$
However, this is not possible since
$\mathrm {dist}(u,\mathrm {ker}(B))\geq |u|\sin \theta \geq ({e^{-r}\sin \theta })/{2}.$
However, this is not possible since
 $$ \begin{align*} \mathrm{dist}(u,\mathrm{ker}(B))&\leq |u-A(s)(x)|+\mathrm{dist}(A(s)(x),\mathrm{ker}(B))\\ &\leq na+ C_1 \cdot \frac{\rho}{\mathrm{dist}(Q_1,Q_2)} < \frac{e^{-r}\sin \theta}{2}. \end{align*} $$
$$ \begin{align*} \mathrm{dist}(u,\mathrm{ker}(B))&\leq |u-A(s)(x)|+\mathrm{dist}(A(s)(x),\mathrm{ker}(B))\\ &\leq na+ C_1 \cdot \frac{\rho}{\mathrm{dist}(Q_1,Q_2)} < \frac{e^{-r}\sin \theta}{2}. \end{align*} $$
Given that
![]() $\textrm {dim}_{\mathbb {R}}\mathbb {C}^A\geq l$
, the transversality condition implies
$\textrm {dim}_{\mathbb {R}}\mathbb {C}^A\geq l$
, the transversality condition implies
![]() $\mathrm {ker}(B)+\mathbb {C}^A=\mathbb {C}^n$
. Let
$\mathrm {ker}(B)+\mathbb {C}^A=\mathbb {C}^n$
. Let
![]() $L=\mathbb {C}^A\cap (\mathrm {ker}(B)\cap \mathbb {C}^A)^{\perp }$
. Define the
$L=\mathbb {C}^A\cap (\mathrm {ker}(B)\cap \mathbb {C}^A)^{\perp }$
. Define the
![]() $\mathbb {R}$
-linear function
$\mathbb {R}$
-linear function
![]() $\hat {x}:\mathbb {C}^n\to \mathbb {C}^n$
given by
$\hat {x}:\mathbb {C}^n\to \mathbb {C}^n$
given by
![]() $\hat {x}(z_1,\ldots ,z_n)=(e^{\chi _1+i\phi _1}\cdot z_1,\ldots ,e^{\chi _n+i\phi _n}\cdot z_n).$
Notice that
$\hat {x}(z_1,\ldots ,z_n)=(e^{\chi _1+i\phi _1}\cdot z_1,\ldots ,e^{\chi _n+i\phi _n}\cdot z_n).$
Notice that
![]() $A(s)(x)=\hat {x}([s])$
, where
$A(s)(x)=\hat {x}([s])$
, where
![]() $[s]=(e^{t_1+iv_1},\ldots ,e^{t_{n-1}+iv_{n-1}},e^{iv_n}).$
Write
$[s]=(e^{t_1+iv_1},\ldots ,e^{t_{n-1}+iv_{n-1}},e^{iv_n}).$
Write
![]() $\hat {x}([s])=b_1+b_2$
, where
$\hat {x}([s])=b_1+b_2$
, where
![]() $b_1\in L$
,
$b_1\in L$
,
![]() $b_2\in \mathrm {ker}(B)$
. The second lemma in linear algebra implies
$b_2\in \mathrm {ker}(B)$
. The second lemma in linear algebra implies
 $$ \begin{align*}|b_1|\leq \frac{\mathrm{dist}(b_1,\mathrm{ker}(B))}{\sin \theta}=\frac{\mathrm{dist}(\hat{x}([s]),\mathrm{ker}(B))}{\sin \theta}=O\bigg(\frac{\rho}{\mathrm{dist}(Q_1,Q_2)}\bigg).\end{align*} $$
$$ \begin{align*}|b_1|\leq \frac{\mathrm{dist}(b_1,\mathrm{ker}(B))}{\sin \theta}=\frac{\mathrm{dist}(\hat{x}([s]),\mathrm{ker}(B))}{\sin \theta}=O\bigg(\frac{\rho}{\mathrm{dist}(Q_1,Q_2)}\bigg).\end{align*} $$
Given that
![]() $b_1\in \mathbb {C}^A$
, we get that
$b_1\in \mathbb {C}^A$
, we get that
![]() $|\hat {x}^{-1}(b_1)|=O({\rho }/{\mathrm {dist}(Q_1,Q_2)})$
. Therefore,
$|\hat {x}^{-1}(b_1)|=O({\rho }/{\mathrm {dist}(Q_1,Q_2)})$
. Therefore,
![]() $[s]=\hat {x}^{-1}(b_1)+ \hat {x}^{-1}(b_2)$
implies
$[s]=\hat {x}^{-1}(b_1)+ \hat {x}^{-1}(b_2)$
implies
 $$ \begin{align*}\mathrm{dist}([s],\hat{x}^{-1}(\mathrm{ker}(B)))=O\bigg(\frac{\rho}{\mathrm{dist}(Q_1,Q_2)}\bigg).\end{align*} $$
$$ \begin{align*}\mathrm{dist}([s],\hat{x}^{-1}(\mathrm{ker}(B)))=O\bigg(\frac{\rho}{\mathrm{dist}(Q_1,Q_2)}\bigg).\end{align*} $$
This last inequality tells us that the vector
![]() $[s]$
is close to a
$[s]$
is close to a
![]() $2n-l$
subspace. Moreover, the last coordinate of this vector has modulus 1. This two properties will allow us to obtain the desired estimate.
$2n-l$
subspace. Moreover, the last coordinate of this vector has modulus 1. This two properties will allow us to obtain the desired estimate.
Consider the set
We have proven that there is a constant
![]() $C_2>0$
, depending only on B and r, such that
$C_2>0$
, depending only on B and r, such that
![]() $\mathrm {dist}([s],\hat {x}^{-1}(\mathrm {ker}(B))) \leq C_2 \cdot {\rho }/{\mathrm {dist}(Q_1,Q_2)}.$
Thus, there is a constant
$\mathrm {dist}([s],\hat {x}^{-1}(\mathrm {ker}(B))) \leq C_2 \cdot {\rho }/{\mathrm {dist}(Q_1,Q_2)}.$
Thus, there is a constant
![]() $C_3>0$
, depending only on B and r, such that
$C_3>0$
, depending only on B and r, such that
In fact, let
![]() $u=(u_1,\ldots ,u_n)\in \hat {x}^{-1}(\mathrm {ker}(B))$
such that
$u=(u_1,\ldots ,u_n)\in \hat {x}^{-1}(\mathrm {ker}(B))$
such that
![]() $|u-[s]|\leq C_2\cdot {\rho }/{\mathrm {dist}(Q_1,Q_2)}$
. We have
$|u-[s]|\leq C_2\cdot {\rho }/{\mathrm {dist}(Q_1,Q_2)}$
. We have
and
for
![]() $j=1,\ldots ,n-1$
. Therefore, if
$j=1,\ldots ,n-1$
. Therefore, if
![]() ${\rho }/{\mathrm {dist}(Q_1,Q_2)}$
is small enough, one has that
${\rho }/{\mathrm {dist}(Q_1,Q_2)}$
is small enough, one has that
![]() $u/|u_n|$
is in H and
$u/|u_n|$
is in H and
![]() $|[s]-(u/|u_n|)|=O({\rho }/{\mathrm {dist}(Q_1,Q_2)})$
. If
$|[s]-(u/|u_n|)|=O({\rho }/{\mathrm {dist}(Q_1,Q_2)})$
. If
![]() ${\rho }/{\mathrm {dist}(Q_1,Q_2)}$
is big, the proposition follows choosing C properly, as it was done before when we considered the case
${\rho }/{\mathrm {dist}(Q_1,Q_2)}$
is big, the proposition follows choosing C properly, as it was done before when we considered the case
![]() ${\rho }/{\mathrm {dist}(Q_1,Q_2)} \geq ({e^{-r} \sin \theta })/{4 C_1}$
.
${\rho }/{\mathrm {dist}(Q_1,Q_2)} \geq ({e^{-r} \sin \theta })/{4 C_1}$
.
Define the function
 $$ \begin{align*}\varphi:\bigg\{(z_1,\ldots,z_n) \in \mathbb{S}^{2n-1} \cap \hat{x}^{-1}( \mathrm{ker}(B)): \,\frac{|z_j|}{|z_n|}\in [e^{-2r},e^{2r}],\,j=1,\ldots,n-1\bigg\} \to H,\end{align*} $$
$$ \begin{align*}\varphi:\bigg\{(z_1,\ldots,z_n) \in \mathbb{S}^{2n-1} \cap \hat{x}^{-1}( \mathrm{ker}(B)): \,\frac{|z_j|}{|z_n|}\in [e^{-2r},e^{2r}],\,j=1,\ldots,n-1\bigg\} \to H,\end{align*} $$
given by
![]() $\varphi (z_1,\ldots ,z_n)=(z_1/|z_n|,\ldots ,z_n/|z_n|).$
Notice that
$\varphi (z_1,\ldots ,z_n)=(z_1/|z_n|,\ldots ,z_n/|z_n|).$
Notice that
![]() $\varphi $
is surjective and smooth. Moreover, one has that
$\varphi $
is surjective and smooth. Moreover, one has that
![]() $\|D\varphi \|$
is bounded by a constant depending only on r and n. Since the domain of
$\|D\varphi \|$
is bounded by a constant depending only on r and n. Since the domain of
![]() $\varphi $
is contained in a
$\varphi $
is contained in a
![]() $(2n-l-1)$
-dimensional unit sphere inside
$(2n-l-1)$
-dimensional unit sphere inside
![]() $\hat {x}^{-1}(\mathrm {ker}(B))$
, there exist
$\hat {x}^{-1}(\mathrm {ker}(B))$
, there exist
![]() $w_1,\ldots ,w_p\in H$
such that H is covered by the balls
$w_1,\ldots ,w_p\in H$
such that H is covered by the balls
![]() $B_{{\rho }/{\mathrm {dist}(Q_1,Q_2)}}(w_j)$
,
$B_{{\rho }/{\mathrm {dist}(Q_1,Q_2)}}(w_j)$
,
![]() $j=1,\ldots ,p$
, and
$j=1,\ldots ,p$
, and
 $$ \begin{align*}p=O\bigg(\bigg(\frac{\rho}{\mathrm{dist}(Q_1,Q_2)}\bigg)^{-(2n-l-1)}\bigg).\end{align*} $$
$$ \begin{align*}p=O\bigg(\bigg(\frac{\rho}{\mathrm{dist}(Q_1,Q_2)}\bigg)^{-(2n-l-1)}\bigg).\end{align*} $$
We conclude that
![]() $[s]\in \bigcup _{j=1}^{p} B_{C_4\cdot {\rho }/{\mathrm {dist}(Q_1,Q_2)}}(w_j),$
for a constant
$[s]\in \bigcup _{j=1}^{p} B_{C_4\cdot {\rho }/{\mathrm {dist}(Q_1,Q_2)}}(w_j),$
for a constant
![]() $C_4>0$
depending only on r and B.
$C_4>0$
depending only on r and B.
Writing
![]() $w_j$
as
$w_j$
as
![]() $w_j=(w_{j,1},\ldots ,w_{j,n}),$
we obtain that for some
$w_j=(w_{j,1},\ldots ,w_{j,n}),$
we obtain that for some
![]() $1\leq j\leq p$
,
$1\leq j\leq p$
,
![]() $q=1,\ldots ,n-1$
. Notice that
$q=1,\ldots ,n-1$
. Notice that
![]() $|w_{j,q}|$
is bounded below by
$|w_{j,q}|$
is bounded below by
![]() $e^{-2r}$
, and hence
$e^{-2r}$
, and hence
![]() $q=1,\ldots ,n$
, where
$q=1,\ldots ,n$
, where
![]() $C_5$
is a constant depending only on r and B, and
$C_5$
is a constant depending only on r and B, and
![]() $\text {arg}(w_{j,q})\in \mathbb {T}$
is the argument of
$\text {arg}(w_{j,q})\in \mathbb {T}$
is the argument of
![]() $w_{j,q}$
. This implies that the set
$w_{j,q}$
. This implies that the set
![]() $\{s\in J_r: B\circ A(s)(Q_1) \cap B\circ A(s)(Q_2)\neq \emptyset \}$
is contained in the union of p sets, each one with a
$\{s\in J_r: B\circ A(s)(Q_1) \cap B\circ A(s)(Q_2)\neq \emptyset \}$
is contained in the union of p sets, each one with a
![]() $\nu $
-volume of order
$\nu $
-volume of order
![]() $O ( ( {\rho }/{\mathrm {dist}(Q_1,Q_2)})^{2n-1} )$
. Finally, using the order of p, we conclude that
$O ( ( {\rho }/{\mathrm {dist}(Q_1,Q_2)})^{2n-1} )$
. Finally, using the order of p, we conclude that
 $$ \begin{align*}\nu(\{s\in J_r: B\circ A(s)(Q_1) \cap B\circ A(s)(Q_2)\neq \emptyset\})= O \bigg(\bigg(\frac{\rho}{\mathrm{dist}(Q_1,Q_2)}\bigg)^{(2n-1)-(2n-l-1)}\bigg),\end{align*} $$
$$ \begin{align*}\nu(\{s\in J_r: B\circ A(s)(Q_1) \cap B\circ A(s)(Q_2)\neq \emptyset\})= O \bigg(\bigg(\frac{\rho}{\mathrm{dist}(Q_1,Q_2)}\bigg)^{(2n-1)-(2n-l-1)}\bigg),\end{align*} $$
as we wanted.
Proposition 3.1 implies that there is a constant
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $\underline {\theta }^1,\ldots ,\underline {\theta }^n$
and
$\underline {\theta }^1,\ldots ,\underline {\theta }^n$
and
![]() $Q_1,Q_2\in R( \rho )$
, we have
$Q_1,Q_2\in R( \rho )$
, we have
 $$ \begin{align*}\nu(\{s\in J_r: B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_1) \cap B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_2)\neq \emptyset\})\leq C \bigg(\frac{\rho}{\mathrm{ dist}(Q_1,Q_2)}\bigg)^l.\end{align*} $$
$$ \begin{align*}\nu(\{s\in J_r: B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_1) \cap B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_2)\neq \emptyset\})\leq C \bigg(\frac{\rho}{\mathrm{ dist}(Q_1,Q_2)}\bigg)^l.\end{align*} $$
The constant
![]() $C>0$
depends on B, r,
$C>0$
depends on B, r,
![]() $c_0$
, and the Cantor sets
$c_0$
, and the Cantor sets
![]() $K_1,\ldots ,K_n$
, but it is independent of
$K_1,\ldots ,K_n$
, but it is independent of
![]() $\rho $
. For the next proposition, we will also need the following fact: if p is big enough, then for any
$\rho $
. For the next proposition, we will also need the following fact: if p is big enough, then for any
![]() $Q_1\in R(\rho )$
and
$Q_1\in R(\rho )$
and
![]() $a\in \mathbb {Z}$
, we have
$a\in \mathbb {Z}$
, we have
where
![]() $d_j=HD(K_j)$
,
$d_j=HD(K_j)$
,
![]() $j=1,\ldots ,n$
. For a proof, see [Reference Zamudio13, Lemma 1.2.3].
$j=1,\ldots ,n$
. For a proof, see [Reference Zamudio13, Lemma 1.2.3].
Proposition 3.2. Assume
![]() $d_1+\cdots +d_n< l$
. Let
$d_1+\cdots +d_n< l$
. Let
 $$ \begin{align*}&N_{\rho}(\underline{\theta}^1,\ldots,\underline{\theta}^n,s)\\&\quad=\# \{(Q_1,Q_2)\in R(\rho)^2: B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_1) \cap B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_2)\neq \emptyset \}.\end{align*} $$
$$ \begin{align*}&N_{\rho}(\underline{\theta}^1,\ldots,\underline{\theta}^n,s)\\&\quad=\# \{(Q_1,Q_2)\in R(\rho)^2: B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_1) \cap B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_2)\neq \emptyset \}.\end{align*} $$
Then for any
![]() $\underline {\theta }^1,\ldots ,\underline {\theta }^n$
, we have
$\underline {\theta }^1,\ldots ,\underline {\theta }^n$
, we have
![]() $\int _{J_r}N_{\rho }(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)ds=O(\rho ^{-(d_1+\cdots +d_j)}),$
and the constant in the O notation is independent of
$\int _{J_r}N_{\rho }(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)ds=O(\rho ^{-(d_1+\cdots +d_j)}),$
and the constant in the O notation is independent of
![]() $\underline {\theta }^1,\ldots ,\underline {\theta }^n$
.
$\underline {\theta }^1,\ldots ,\underline {\theta }^n$
.
Proof. Since the Cantor sets
![]() $K_1,\ldots ,K_n$
have bounded geometries, then there is a constant
$K_1,\ldots ,K_n$
have bounded geometries, then there is a constant
![]() $C_1$
, independent of
$C_1$
, independent of
![]() $\rho $
, such that
$\rho $
, such that
![]() $\mathrm {dist}(Q_1,Q_2)\geq C_1 \rho $
for any
$\mathrm {dist}(Q_1,Q_2)\geq C_1 \rho $
for any
![]() $Q_1,Q_2\in R(\rho )$
,
$Q_1,Q_2\in R(\rho )$
,
![]() $Q_1\cap Q_2=\emptyset $
. Let
$Q_1\cap Q_2=\emptyset $
. Let
![]() $k_0\in \mathbb {Z}$
such that
$k_0\in \mathbb {Z}$
such that
![]() $p^{-k_0}\leq C_1 \rho < p^{-k_0+1}$
. Using the previous lemma, we have
$p^{-k_0}\leq C_1 \rho < p^{-k_0+1}$
. Using the previous lemma, we have
 $$ \begin{align*} &\int_{J_r} N_{\rho}(\underline{\theta}^1,\ldots,\underline{\theta}^n,s)\,ds\\ &\quad= \sum_{Q_1,Q_2 \in R(\rho)} \nu(\{s\in J_r: B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_1) \cap B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_2)\neq \emptyset \})\\ &\quad=\sum_{Q_1 \in R(\rho)} \sum_{k=-\infty}^{k_0} \sum_{\mathrm{dist}(Q_1,Q_2)\in [p^{-k},p^{-k+1})} O(\rho^l/[\mathrm{dist}(Q_1,Q_2)]^l)\\ &\qquad+ \sum_{Q_1 \in R(\rho)} \sum_{Q_2 \cap Q_1\neq \emptyset} (2r)^{n-1}. \end{align*} $$
$$ \begin{align*} &\int_{J_r} N_{\rho}(\underline{\theta}^1,\ldots,\underline{\theta}^n,s)\,ds\\ &\quad= \sum_{Q_1,Q_2 \in R(\rho)} \nu(\{s\in J_r: B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_1) \cap B\circ \pi_{\underline{\theta}^1,\ldots,\underline{\theta}^n,s}(Q_2)\neq \emptyset \})\\ &\quad=\sum_{Q_1 \in R(\rho)} \sum_{k=-\infty}^{k_0} \sum_{\mathrm{dist}(Q_1,Q_2)\in [p^{-k},p^{-k+1})} O(\rho^l/[\mathrm{dist}(Q_1,Q_2)]^l)\\ &\qquad+ \sum_{Q_1 \in R(\rho)} \sum_{Q_2 \cap Q_1\neq \emptyset} (2r)^{n-1}. \end{align*} $$
Clearly,
![]() $\sum _{Q_1 \in R(\rho )} \sum _{Q_2 \cap Q_1\neq \emptyset } (2r)^{n-1}=O(\# R(\rho ))=O(\rho ^{-(d_1+\cdots +d_n)}).$
However,
$\sum _{Q_1 \in R(\rho )} \sum _{Q_2 \cap Q_1\neq \emptyset } (2r)^{n-1}=O(\# R(\rho ))=O(\rho ^{-(d_1+\cdots +d_n)}).$
However,
 $$ \begin{align*} &\sum_{Q_1 \in R(\rho)} \sum_{k=-\infty}^{k_0} \sum_{\mathrm{dist}(Q_1,Q_2)\in [p^{-k},p^{-k+1})} O(\rho^l/[\mathrm{dist}(Q_1,Q_2)]^l)\\ &\quad=\sum_{Q_1 \in R(\rho)} \sum_{k=-\infty}^{k_0} O((p^k)^{l-(d_1+\cdots+d_n)}\rho^{l-(d_1+\cdots+d_n)})\\ &\quad=\sum_{Q_1 \in R(\rho)} O((p^{k_0})^{l-(d_1+\cdots+d_n)}\rho^{l-(d_1+\cdots+d_n)})\sum_{k=-\infty}^{0} (p^{l-(d_1+\cdots+d_n)})^k\\ &\quad= O(\rho^{-(d_1+\cdots+d_n)}\rho^{-l+(d_1+\cdots+d_l)}\rho^{l-(d_1+\cdots+d_n)})=O(\rho^{-(d_1+\cdots+d_n)}).\\[-3pc] \end{align*} $$
$$ \begin{align*} &\sum_{Q_1 \in R(\rho)} \sum_{k=-\infty}^{k_0} \sum_{\mathrm{dist}(Q_1,Q_2)\in [p^{-k},p^{-k+1})} O(\rho^l/[\mathrm{dist}(Q_1,Q_2)]^l)\\ &\quad=\sum_{Q_1 \in R(\rho)} \sum_{k=-\infty}^{k_0} O((p^k)^{l-(d_1+\cdots+d_n)}\rho^{l-(d_1+\cdots+d_n)})\\ &\quad=\sum_{Q_1 \in R(\rho)} O((p^{k_0})^{l-(d_1+\cdots+d_n)}\rho^{l-(d_1+\cdots+d_n)})\sum_{k=-\infty}^{0} (p^{l-(d_1+\cdots+d_n)})^k\\ &\quad= O(\rho^{-(d_1+\cdots+d_n)}\rho^{-l+(d_1+\cdots+d_l)}\rho^{l-(d_1+\cdots+d_n)})=O(\rho^{-(d_1+\cdots+d_n)}).\\[-3pc] \end{align*} $$
Proposition 3.3. Let
![]() $b>0$
,
$b>0$
,
![]() $F\subset R(\rho )$
such that
$F\subset R(\rho )$
such that
![]() $\#F\geq b\rho ^{-(d_1+\cdots +d_n)}$
. Let
$\#F\geq b\rho ^{-(d_1+\cdots +d_n)}$
. Let
![]() $(\underline {\theta }^1,\ldots , \underline {\theta }^n,s)$
such that
$(\underline {\theta }^1,\ldots , \underline {\theta }^n,s)$
such that
![]() $N_{\rho }(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\leq a \rho ^{-(d_1+\cdots +d_n)}$
, then there exists a subset
$N_{\rho }(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\leq a \rho ^{-(d_1+\cdots +d_n)}$
, then there exists a subset
![]() $T\subset F$
with the properties that
$T\subset F$
with the properties that
![]() $B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_1) \cap B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_2)= \emptyset $
for all
$B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_1) \cap B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_2)= \emptyset $
for all
![]() $Q_1,Q_2 \in T$
,
$Q_1,Q_2 \in T$
,
![]() $Q_1\neq Q_2$
, and
$Q_1\neq Q_2$
, and
![]() $\#T \geq ({b^2}/{4a})\rho ^{-(d_1+\cdots +d_n)}.$
$\#T \geq ({b^2}/{4a})\rho ^{-(d_1+\cdots +d_n)}.$
Proof. For
![]() $Q_0\in F$
, define
$Q_0\in F$
, define
We have
![]() $\sum _{Q \in F} n(Q)\leq N_{\rho }(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s) \leq a \rho ^{-(d_1+\cdots +d_n)}. $
Therefore, the set
$\sum _{Q \in F} n(Q)\leq N_{\rho }(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s) \leq a \rho ^{-(d_1+\cdots +d_n)}. $
Therefore, the set
![]() $T_0=\{Q\in F: n(Q)\leq 2a/b\}$
has at least
$T_0=\{Q\in F: n(Q)\leq 2a/b\}$
has at least
![]() $(1/2)\#F$
elements. Finally, it is clear that from
$(1/2)\#F$
elements. Finally, it is clear that from
![]() $T_0$
, we can extract a subset T with at least
$T_0$
, we can extract a subset T with at least
![]() $({1}/({2a/b}))\#T_0$
elements and such that
$({1}/({2a/b}))\#T_0$
elements and such that
![]() $B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_1) \cap B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_2)= \emptyset $
for any
$B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_1) \cap B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_2)= \emptyset $
for any
![]() $Q_1,Q_2 \in T$
. For this set, we have
$Q_1,Q_2 \in T$
. For this set, we have
 $$ \begin{align*}\#T \geq \frac{1}{2a/b}\#T_0 \geq \frac{1}{2a/b}\frac{1}{2}b \rho^{-(d_1+\cdots+d_n)}=\frac{b^2}{4a}\rho^{-(d_1+\cdots+d_n)}.\\[-38pt]\end{align*} $$
$$ \begin{align*}\#T \geq \frac{1}{2a/b}\#T_0 \geq \frac{1}{2a/b}\frac{1}{2}b \rho^{-(d_1+\cdots+d_n)}=\frac{b^2}{4a}\rho^{-(d_1+\cdots+d_n)}.\\[-38pt]\end{align*} $$
Notice that since
![]() $\int _{J_r} N_{\rho }(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\,ds=O(\rho ^{-(d_1+\cdots +d_m)})$
, then choosing a big enough, we can guarantee that the set
$\int _{J_r} N_{\rho }(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\,ds=O(\rho ^{-(d_1+\cdots +d_m)})$
, then choosing a big enough, we can guarantee that the set
has measure as small as we want. Thus, for every
![]() $(\underline {\theta }^1,\ldots ,\underline {\theta }^n)$
, we have that most of the
$(\underline {\theta }^1,\ldots ,\underline {\theta }^n)$
, we have that most of the
![]() $s\in J_r$
verify the property of the last proposition, that is, for any family
$s\in J_r$
verify the property of the last proposition, that is, for any family
![]() $F\subset R(\rho )$
with
$F\subset R(\rho )$
with
![]() $\# F\geq b\rho ^{-(d_1+\cdots +d_n)}$
, there exist a positive proportion of F,
$\# F\geq b\rho ^{-(d_1+\cdots +d_n)}$
, there exist a positive proportion of F,
![]() $T\subset F$
with
$T\subset F$
with
![]() $\#T\geq (b^2/(4a))\rho ^{-(d_1+\cdots +d_n)}$
, such that elements of T project to
$\#T\geq (b^2/(4a))\rho ^{-(d_1+\cdots +d_n)}$
, such that elements of T project to
![]() $\mathbb {R}^l$
, in the direction of s, to disjoint sets:
$\mathbb {R}^l$
, in the direction of s, to disjoint sets:
![]() $B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_1) \cap B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_2)=\emptyset \ \text { for all } Q_1,Q_2 \in T$
. This is what we call the discrete Marstrand property.
$B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_1) \cap B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}(Q_2)=\emptyset \ \text { for all } Q_1,Q_2 \in T$
. This is what we call the discrete Marstrand property.
The next lemma guarantees that the property of Proposition 3.3 still holds for small perturbations of
![]() $B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}$
; it is inspired in the presentation given by Shmerkin [Reference Shmerkin12].
$B\circ \pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}$
; it is inspired in the presentation given by Shmerkin [Reference Shmerkin12].
Lemma 3.4. Let
![]() $T\subset R(\rho )$
,
$T\subset R(\rho )$
,
![]() $\phi $
a function defined on a neighborhood of
$\phi $
a function defined on a neighborhood of
![]() $\bigcup _{Q\in T} Q$
into
$\bigcup _{Q\in T} Q$
into
![]() $\mathbb {R}^l$
, and
$\mathbb {R}^l$
, and
![]() $L,\tau>0$
real numbers. Suppose that for each
$L,\tau>0$
real numbers. Suppose that for each
![]() $Q\in T$
, we have
$Q\in T$
, we have
![]() $B_{L^{-1}\rho }(c_Q)\subset \phi (Q) \subset B_{L\rho }(c_Q)$
for some
$B_{L^{-1}\rho }(c_Q)\subset \phi (Q) \subset B_{L\rho }(c_Q)$
for some
![]() $c_Q\in \mathbb {R}^l$
, and
$c_Q\in \mathbb {R}^l$
, and
![]() $\phi (Q_1)\cap \phi (Q_2)= \emptyset \ \text { for all } Q_1,Q_2\in T$
,
$\phi (Q_1)\cap \phi (Q_2)= \emptyset \ \text { for all } Q_1,Q_2\in T$
,
![]() $Q_1\neq Q_2$
. Then for any
$Q_1\neq Q_2$
. Then for any
![]() $\psi $
defined on a neighborhood of
$\psi $
defined on a neighborhood of
![]() $\bigcup _{Q\in T} Q$
, such that the supremum norm
$\bigcup _{Q\in T} Q$
, such that the supremum norm
![]() $\|\phi - \psi \|<\tau \rho $
, there exists
$\|\phi - \psi \|<\tau \rho $
, there exists
![]() $T'\subset T$
such that
$T'\subset T$
such that
and
![]() $\psi (Q_1)\cap \psi (Q_2)= \emptyset \ \text { for all } Q_1,Q_2\in T'$
,
$\psi (Q_1)\cap \psi (Q_2)= \emptyset \ \text { for all } Q_1,Q_2\in T'$
,
![]() $Q_1\neq Q_2$
.
$Q_1\neq Q_2$
.
Proof. Here,
![]() $\|\psi -\phi \|<\tau \rho $
implies
$\|\psi -\phi \|<\tau \rho $
implies
![]() $\psi (Q)\subset B_{(L+\tau )\rho }(c_Q)$
. Use the Vitali covering lemma for the family
$\psi (Q)\subset B_{(L+\tau )\rho }(c_Q)$
. Use the Vitali covering lemma for the family
![]() $\{B_{(L+\tau )\rho }(c_Q):Q\in T\}$
. We get
$\{B_{(L+\tau )\rho }(c_Q):Q\in T\}$
. We get
![]() $T'\subset T$
such that
$T'\subset T$
such that
![]() $\{B_{(L+\tau )\rho }(c_Q):Q\in T'\}$
is a pairwise disjoint family and
$\{B_{(L+\tau )\rho }(c_Q):Q\in T'\}$
is a pairwise disjoint family and
![]() $\bigcup _{Q\in T} B_{(L+\tau )\rho }(c_Q)\subset \bigcup _{Q\in T'} B_{3(L+\tau )\rho }(c_Q).$
From this, we get
$\bigcup _{Q\in T} B_{(L+\tau )\rho }(c_Q)\subset \bigcup _{Q\in T'} B_{3(L+\tau )\rho }(c_Q).$
From this, we get
 $$ \begin{align*} \# T' \cdot [3(L+\tau)\rho]^l w_l &\geq \mathrm{Vol}\bigg(\bigcup_{Q\in T} B_{(L+\tau)\rho}(c_Q)\bigg) \\ &\geq \mathrm{Vol}\bigg(\bigcup_{Q\in T} B_{L^{-1}\rho}(c_Q)\bigg) \\ &=\#T\cdot L^{-l}\rho^l w_l, \end{align*} $$
$$ \begin{align*} \# T' \cdot [3(L+\tau)\rho]^l w_l &\geq \mathrm{Vol}\bigg(\bigcup_{Q\in T} B_{(L+\tau)\rho}(c_Q)\bigg) \\ &\geq \mathrm{Vol}\bigg(\bigcup_{Q\in T} B_{L^{-1}\rho}(c_Q)\bigg) \\ &=\#T\cdot L^{-l}\rho^l w_l, \end{align*} $$
where
![]() $w_l$
is the volume of the l-dimensional unitary ball. Hence,
$w_l$
is the volume of the l-dimensional unitary ball. Hence,
3.2 Proof of the dimension formula
In this subsection, we prove the desired dimension formula (Theorem B). Assume we have
![]() $K_1,\ldots ,K_n$
satisfying the hypothesis of the scale recurrence lemma. We start by using the discrete Marstrand property and the scale recurrence lemma to obtain, for each limit geometry
$K_1,\ldots ,K_n$
satisfying the hypothesis of the scale recurrence lemma. We start by using the discrete Marstrand property and the scale recurrence lemma to obtain, for each limit geometry
![]() $(\underline {\theta }^1,\ldots ,\underline {\theta }^n)$
, a set of ‘good’ directions to project. Fix
$(\underline {\theta }^1,\ldots ,\underline {\theta }^n)$
, a set of ‘good’ directions to project. Fix
![]() $c_0,r>0$
big enough, and let
$c_0,r>0$
big enough, and let
![]() $c_1,c_2,c_3,\rho _0$
be the constants given by the scale recurrence lemma. Suppose that h is a
$c_1,c_2,c_3,\rho _0$
be the constants given by the scale recurrence lemma. Suppose that h is a
![]() $C^{1}$
function defined from a neighborhood of
$C^{1}$
function defined from a neighborhood of
![]() $K_1\times \cdots \times K_n$
into
$K_1\times \cdots \times K_n$
into
![]() $\mathbb {R}^l$
such that there exists a point
$\mathbb {R}^l$
such that there exists a point
![]() $x_0\in K_1\times \cdots \times K_n$
, where
$x_0\in K_1\times \cdots \times K_n$
, where
![]() $B=Dh(x_0)$
verifies the transversality hypotheses. By the results in §3.1, we can fix
$B=Dh(x_0)$
verifies the transversality hypotheses. By the results in §3.1, we can fix
![]() $a>0$
big enough such that
$a>0$
big enough such that
for all
![]() $(\underline {\theta }^1,\ldots ,\underline {\theta }^n)$
. Define
$(\underline {\theta }^1,\ldots ,\underline {\theta }^n)$
. Define
and for
![]() $(\underline {a}^1,\ldots ,\underline {a}^n)\in \Sigma _{1}(c_0,\rho )\times \cdots \times \Sigma _{n}(c_0,\rho )$
,
$(\underline {a}^1,\ldots ,\underline {a}^n)\in \Sigma _{1}(c_0,\rho )\times \cdots \times \Sigma _{n}(c_0,\rho )$
,
 $$ \begin{align*}F(\underline{a}^1,\ldots,\underline{a}^n)=\bigcup_{\underline{\theta}^1,\ldots,\underline{\theta}^n} F(\underline{\theta}^1,\ldots,\underline{\theta}^n),\end{align*} $$
$$ \begin{align*}F(\underline{a}^1,\ldots,\underline{a}^n)=\bigcup_{\underline{\theta}^1,\ldots,\underline{\theta}^n} F(\underline{\theta}^1,\ldots,\underline{\theta}^n),\end{align*} $$
where the union is over all
![]() $\underline {\theta }^1,\ldots ,\underline {\theta }^n$
ending in
$\underline {\theta }^1,\ldots ,\underline {\theta }^n$
ending in
![]() $\underline {a}^1,\ldots ,\underline {a}^n$
, respectively. We clearly have
$\underline {a}^1,\ldots ,\underline {a}^n$
, respectively. We clearly have
![]() $\nu (J_r\setminus F(\underline {a}^1,\ldots ,\underline {a}^n))<c_1$
, and thus we can apply the scale recurrence lemma (from now on, we assume
$\nu (J_r\setminus F(\underline {a}^1,\ldots ,\underline {a}^n))<c_1$
, and thus we can apply the scale recurrence lemma (from now on, we assume
![]() $\rho <\rho _0$
) to obtain sets
$\rho <\rho _0$
) to obtain sets
![]() $F^*(\underline {a}^1,\ldots ,\underline {a}^n)$
with the three properties in Theorem A (see §2.6).
$F^*(\underline {a}^1,\ldots ,\underline {a}^n)$
with the three properties in Theorem A (see §2.6).
Theorem 3.1. Suppose that
![]() $d_1+\cdots +d_n<l$
and for any
$d_1+\cdots +d_n<l$
and for any
![]() $(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in \Sigma _1^-\times \cdots \times \Sigma _n^-\hspace{-0.2pt}\times\hspace{-0.2pt} J_r$
, there exists
$(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in \Sigma _1^-\times \cdots \times \Sigma _n^-\hspace{-0.2pt}\times\hspace{-0.2pt} J_r$
, there exists
![]() $(\underline {c}^1,\ldots ,\underline {c}^n)\in \Sigma _1^\textit{fin}\hspace{-0.5pt}\times \cdots \times\hspace{-0.5pt} \Sigma _n^\textit{fin}$
such that
$(\underline {c}^1,\ldots ,\underline {c}^n)\in \Sigma _1^\textit{fin}\hspace{-0.5pt}\times \cdots \times\hspace{-0.5pt} \Sigma _n^\textit{fin}$
such that
![]() $T_{\underline {c}^1,\ldots ,\underline {c}^n}(\underline {\theta }^1,\ldots, \underline {\theta }^n,s)=(\underline {\theta }^1\underline {c}^1,\ldots ,\underline {\theta }^n\underline {c}^n,\tilde {s})$
and
$T_{\underline {c}^1,\ldots ,\underline {c}^n}(\underline {\theta }^1,\ldots, \underline {\theta }^n,s)=(\underline {\theta }^1\underline {c}^1,\ldots ,\underline {\theta }^n\underline {c}^n,\tilde {s})$
and
![]() $\tilde {s}\in F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for some
$\tilde {s}\in F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for some
![]() $(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for which
$(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for which
![]() $(\underline {\theta }^1\underline {c}^1,\ldots ,\underline {\theta }^n\underline {c}^n)$
ends in it. Then
$(\underline {\theta }^1\underline {c}^1,\ldots ,\underline {\theta }^n\underline {c}^n)$
ends in it. Then
![]() $HD(h(K_1\times \cdots \times K_n))=d_1+\cdots +d_n.$
$HD(h(K_1\times \cdots \times K_n))=d_1+\cdots +d_n.$
Proof. Since h is Lipschitz in a neighborhood of
![]() $K_1\times \cdots \times K_n$
and
$K_1\times \cdots \times K_n$
and
![]() $HD(K_1\times \cdots \times K_n)=d_1+\cdots +d_n$
, we have
$HD(K_1\times \cdots \times K_n)=d_1+\cdots +d_n$
, we have
![]() $HD(h(K_1\times \cdots \times K_n))\leq d_1+\cdots +d_n.$
Thus, we only need to show
$HD(h(K_1\times \cdots \times K_n))\leq d_1+\cdots +d_n.$
Thus, we only need to show
![]() $HD(h(K_1\times \cdots \times K_n))\geq d_1+\cdots +d_n$
. Let
$HD(h(K_1\times \cdots \times K_n))\geq d_1+\cdots +d_n$
. Let
![]() $\eta>0$
arbitrary, we will prove that
$\eta>0$
arbitrary, we will prove that
![]() $HD(h(K_1\times \cdots \times K_n))\geq d_1+\cdots +d_n-\eta ,$
this will finish the proof of the theorem.
$HD(h(K_1\times \cdots \times K_n))\geq d_1+\cdots +d_n-\eta ,$
this will finish the proof of the theorem.
Since
![]() $\Sigma _1^-\times \cdots \times \Sigma _n^-\times J_r$
is compact and
$\Sigma _1^-\times \cdots \times \Sigma _n^-\times J_r$
is compact and
![]() $\pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}$
depends continuously in
$\pi _{\underline {\theta }^1,\ldots ,\underline {\theta }^n,s}$
depends continuously in
![]() $(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)$
, then we can choose a constant
$(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)$
, then we can choose a constant
![]() $L>0$
(only depending on r,
$L>0$
(only depending on r,
![]() $K_1,\ldots,K_n$
, and
$K_1,\ldots,K_n$
, and
![]() $Dh(x_0)$
) such that
$Dh(x_0)$
) such that
for some
![]() $c_Q\in \mathbb {R}^l$
, which depends on
$c_Q\in \mathbb {R}^l$
, which depends on
![]() $\underline {\theta }^1,\ldots ,\underline {\theta }^n,s$
and Q.
$\underline {\theta }^1,\ldots ,\underline {\theta }^n,s$
and Q.
Choose
![]() $\tau>0$
big enough such that
$\tau>0$
big enough such that
for all
![]() $\underline {\theta }^j,\tilde {\underline {\theta }}^j\in \Sigma _j^-$
,
$\underline {\theta }^j,\tilde {\underline {\theta }}^j\in \Sigma _j^-$
,
![]() $j=1,\ldots ,n$
,
$j=1,\ldots ,n$
,
![]() $s,\tilde {s}\in J_r$
with
$s,\tilde {s}\in J_r$
with
![]() $|s-\tilde {s}|<c_2\rho $
,
$|s-\tilde {s}|<c_2\rho $
,
![]() $\underline {\theta }^j\wedge \tilde {\underline {\theta }}^j\in \Sigma _j(c_0,\rho )$
,
$\underline {\theta }^j\wedge \tilde {\underline {\theta }}^j\in \Sigma _j(c_0,\rho )$
,
![]() $j=1,\ldots ,n$
.
$j=1,\ldots ,n$
.
Until now, all the statements where
![]() $\rho $
appeared were true for any value small enough. For the rest of the proof, we are going to fix a particular value, which we call
$\rho $
appeared were true for any value small enough. For the rest of the proof, we are going to fix a particular value, which we call
![]() $\rho _1$
to distinguish it from the ‘variable’
$\rho _1$
to distinguish it from the ‘variable’
![]() $\rho $
. It is chosen such that
$\rho $
. It is chosen such that
![]() $\rho _1^{\eta }\leq C_3[3L(L+\tau )]^{-l}{c_3^2}/{4a},$
where
$\rho _1^{\eta }\leq C_3[3L(L+\tau )]^{-l}{c_3^2}/{4a},$
where
![]() $C_3>0$
is a constant, independent of
$C_3>0$
is a constant, independent of
![]() $\rho $
, which will be fixed later (equation (5)).
$\rho $
, which will be fixed later (equation (5)).
We can choose
![]() $\underline {a}_0^1,\ldots ,\underline {a}_0^n$
and
$\underline {a}_0^1,\ldots ,\underline {a}_0^n$
and
![]() $\underline {\theta }_0^1,\ldots ,\underline {\theta }_0^n$
ending in it, respectively, with the following properties.
$\underline {\theta }_0^1,\ldots ,\underline {\theta }_0^n$
ending in it, respectively, with the following properties.
(a) The element
![]() $s_0=(\log ({r_{\underline {a}_0^1}}/{r_{\underline {a}_0^n}}),\ldots ,\log ({r_{\underline {a}_0^{n-1}}}/{r_{\underline {a}_0^n}}),v_{\underline {a}_0^1},\ldots ,v_{\underline {a}_0^n})$
is in
$s_0=(\log ({r_{\underline {a}_0^1}}/{r_{\underline {a}_0^n}}),\ldots ,\log ({r_{\underline {a}_0^{n-1}}}/{r_{\underline {a}_0^n}}),v_{\underline {a}_0^1},\ldots ,v_{\underline {a}_0^n})$
is in
![]() $J_r$
.
$J_r$
.
(b)
![]() $x_{0}\in G(\underline {a}_0^1)\times \cdots \times G(\underline {a}_0^n)$
.
$x_{0}\in G(\underline {a}_0^1)\times \cdots \times G(\underline {a}_0^n)$
.
(c) For any
![]() $\underline {b}^1,\ldots ,\underline {b}^n$
, consider
$\underline {b}^1,\ldots ,\underline {b}^n$
, consider
![]() $\tilde {s}=(\log ({r_{\underline {a}_0^1\underline {b}^1}}/{r_{\underline {a}_0^n\underline {b}^n}}),\ldots ,\log ({r_{\underline {a}_0^{n-1}\underline {b}^{n-1}}}/{r_{\underline {a}_0^n\underline {b}^n}}), v_{\underline {a}_0^1\underline {b}^1},\ldots ,v_{\underline {a}_0^n\underline {b}^n}).$
Then
$\tilde {s}=(\log ({r_{\underline {a}_0^1\underline {b}^1}}/{r_{\underline {a}_0^n\underline {b}^n}}),\ldots ,\log ({r_{\underline {a}_0^{n-1}\underline {b}^{n-1}}}/{r_{\underline {a}_0^n\underline {b}^n}}), v_{\underline {a}_0^1\underline {b}^1},\ldots ,v_{\underline {a}_0^n\underline {b}^n}).$
Then
This is achieved by choosing very long words for
![]() $\underline {a}_0^1,\ldots ,\underline {a}_0^n$
. If the number of symbols in
$\underline {a}_0^1,\ldots ,\underline {a}_0^n$
. If the number of symbols in
![]() $\underline {a}_0^j$
, for
$\underline {a}_0^j$
, for
![]() $1\leq j\leq n$
, increases, then
$1\leq j\leq n$
, increases, then
![]() $|x_0-(c_{\underline {a}_0^1\underline {b}^1},\ldots ,c_{\underline {a}_0^n\underline {b}^n})|$
goes to zero; the same happens for the distance between the last coordinate of
$|x_0-(c_{\underline {a}_0^1\underline {b}^1},\ldots ,c_{\underline {a}_0^n\underline {b}^n})|$
goes to zero; the same happens for the distance between the last coordinate of
![]() $T_{\underline {b}^1,\ldots ,\underline {b}^n}(\underline {\theta }_0^1,\ldots ,\underline {\theta }_0^n,s)$
and
$T_{\underline {b}^1,\ldots ,\underline {b}^n}(\underline {\theta }_0^1,\ldots ,\underline {\theta }_0^n,s)$
and
![]() $\tilde {s}$
. This a consequence of item (b) and the fact that
$\tilde {s}$
. This a consequence of item (b) and the fact that
![]() $r_{\underline {a}_0^j}r^{\underline {\theta }_0^j}_{\underline {b}^j}/r_{\underline {a}_0^j\underline {b}^j} \to 1$
,
$r_{\underline {a}_0^j}r^{\underline {\theta }_0^j}_{\underline {b}^j}/r_{\underline {a}_0^j\underline {b}^j} \to 1$
,
![]() $\|v_{\underline {a}_0^j\underline {b}^j}-(v_{\underline {a}_0^j}+v^{\underline {\theta }_0^j}_{\underline {b}^j})\|\to 0$
as the number of symbols in
$\|v_{\underline {a}_0^j\underline {b}^j}-(v_{\underline {a}_0^j}+v^{\underline {\theta }_0^j}_{\underline {b}^j})\|\to 0$
as the number of symbols in
![]() $\underline {a}_0^j$
goes to infinity.
$\underline {a}_0^j$
goes to infinity.
(d) For any
![]() $\underline {b}^1,\ldots ,\underline {b}^n$
such that
$\underline {b}^1,\ldots ,\underline {b}^n$
such that
![]() $\tilde {s}\in J_r$
, there is an affine function L such that
$\tilde {s}\in J_r$
, there is an affine function L such that
This is a consequence of Lemma 3.1.
By hypothesis, there exists
![]() $(\underline {c}^1,\ldots ,\underline {c}^n)\in \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}$
such that
$(\underline {c}^1,\ldots ,\underline {c}^n)\in \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}$
such that
and
![]() $\tilde {s}_0\in F^*(\tilde {\underline {a}}_0^1,\ldots ,\tilde {\underline {a}}_0^n)$
for some
$\tilde {s}_0\in F^*(\tilde {\underline {a}}_0^1,\ldots ,\tilde {\underline {a}}_0^n)$
for some
![]() $(\tilde {\underline {a}}_0^1,\ldots ,\tilde {\underline {a}}_0^n)$
for which
$(\tilde {\underline {a}}_0^1,\ldots ,\tilde {\underline {a}}_0^n)$
for which
![]() $(\underline {\theta }_0^1\underline {c}^1,\ldots ,\underline {\theta }_0^n\underline {c}^n)$
ends in it.
$(\underline {\theta }_0^1\underline {c}^1,\ldots ,\underline {\theta }_0^n\underline {c}^n)$
ends in it.
We will define inductively a set
![]() $N\subset \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}\times \Sigma _1^-\times \cdots \times \Sigma _n^-\times J_r$
. Every
$N\subset \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}\times \Sigma _1^-\times \cdots \times \Sigma _n^-\times J_r$
. Every
![]() $p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
should verify:
$p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
should verify:
-
(i)
 $s\in F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for some
$s\in F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for some
 $(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
such that
$(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
such that
 $(\underline {\theta }^1,\ldots ,\underline {\theta }^n)$
ends in
$(\underline {\theta }^1,\ldots ,\underline {\theta }^n)$
ends in
 $(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
;
$(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
; -
(ii)
 $(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)=(\underline {a}_0^1\underline {b}^1,\ldots ,\underline {a}_0^n\underline {b}^n,T_{\underline {b}^1,\ldots ,\underline {b}^n}(\underline {\theta }_0^1,\ldots ,\underline {\theta }_0^n,s_0))$
for some
$(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)=(\underline {a}_0^1\underline {b}^1,\ldots ,\underline {a}_0^n\underline {b}^n,T_{\underline {b}^1,\ldots ,\underline {b}^n}(\underline {\theta }_0^1,\ldots ,\underline {\theta }_0^n,s_0))$
for some
 $(\underline {b}^1,\ldots ,\underline {b}^n)\in \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}$
.
$(\underline {b}^1,\ldots ,\underline {b}^n)\in \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}$
.
For
![]() $p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
, we will define a set
$p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
, we will define a set
![]() $T'(p)\subset R(\rho _1)$
verifying:
$T'(p)\subset R(\rho _1)$
verifying:
-
(iii)
 $\#T'(p)\geq C_3^{-1}\rho _1^{\eta -(d_1+\cdots +d_n)}$
;
$\#T'(p)\geq C_3^{-1}\rho _1^{\eta -(d_1+\cdots +d_n)}$
; -
(iv)
 $h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})(Q_1)\cap h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})(Q_2)=\emptyset $
for all
$h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})(Q_1)\cap h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})(Q_2)=\emptyset $
for all
 $Q_1,Q_2\in T'(p)$
,
$Q_1,Q_2\in T'(p)$
,
 $Q_1\neq Q_2$
;
$Q_1\neq Q_2$
; -
(v) for all
 $(\underline {b}^1,\ldots ,\underline {b}^n)\in T'(p)$
, we have
$(\underline {b}^1,\ldots ,\underline {b}^n)\in T'(p)$
, we have
 $T_{\underline {b}^1,\ldots ,\underline {b}^n}(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)=(\underline {\theta }^1\underline {b}^1,\ldots , \underline {\theta }^n\underline {b}^n,\tilde {s})$
and
$T_{\underline {b}^1,\ldots ,\underline {b}^n}(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)=(\underline {\theta }^1\underline {b}^1,\ldots , \underline {\theta }^n\underline {b}^n,\tilde {s})$
and
 $\tilde {s}\in F^*(\underline {b}^1,\ldots ,\underline {b}^n)$
.
$\tilde {s}\in F^*(\underline {b}^1,\ldots ,\underline {b}^n)$
.
Elements of N are defined inductively, that is, every element already defined as
![]() $p\in N$
generates new elements, which we call the children of p and denote by
$p\in N$
generates new elements, which we call the children of p and denote by
![]() $Ch(p)$
. Thus, N has the structure of a rooted tree. The root of the tree is
$Ch(p)$
. Thus, N has the structure of a rooted tree. The root of the tree is
![]() $p_0=(\underline {a}_0^1\underline {c}^1,\ldots ,\underline {a}_0^n\underline {c}^n,\underline {\theta }_0^1\underline {c}^1,\ldots ,\underline {\theta }_0^n\underline {c}^n,\tilde {s}_0)$
, the set
$p_0=(\underline {a}_0^1\underline {c}^1,\ldots ,\underline {a}_0^n\underline {c}^n,\underline {\theta }_0^1\underline {c}^1,\ldots ,\underline {\theta }_0^n\underline {c}^n,\tilde {s}_0)$
, the set
![]() $T'(p_0)$
is defined as described below.
$T'(p_0)$
is defined as described below.
Given
![]() $p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)$
verifying items (i), (ii) (as
$p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)$
verifying items (i), (ii) (as
![]() $p_0$
does), define
$p_0$
does), define
![]() $T'(p)$
in the following way.
$T'(p)$
in the following way.
By item (i), we know that
![]() $s\in F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
, and hence the scale recurrence lemma implies that there exists a set
$s\in F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
, and hence the scale recurrence lemma implies that there exists a set
![]() $F\subset R(\rho _1)$
with
$F\subset R(\rho _1)$
with
![]() $\#F\geq c_3\rho _1^{-(d_1+\cdots +d_n)}$
and such that item (v) holds for F.
$\#F\geq c_3\rho _1^{-(d_1+\cdots +d_n)}$
and such that item (v) holds for F.
Since
![]() $F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)\subset V_{c_2\rho _1}(F(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n))$
, then there exist
$F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)\subset V_{c_2\rho _1}(F(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n))$
, then there exist
![]() $s'\in F(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
with
$s'\in F(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
with
![]() $|s-s'|\leq c_2\rho _1$
. By the definition of
$|s-s'|\leq c_2\rho _1$
. By the definition of
![]() $F(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
, we have
$F(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
, we have
![]() $N_{\rho _1}(\tilde {\underline {\theta }}^1,\ldots ,\tilde {\underline {\theta }}^n,s')\leq a\rho _1^{-(d_1+\cdots +d_n)}$
for some
$N_{\rho _1}(\tilde {\underline {\theta }}^1,\ldots ,\tilde {\underline {\theta }}^n,s')\leq a\rho _1^{-(d_1+\cdots +d_n)}$
for some
![]() $(\tilde {\underline {\theta }}^1,\ldots ,\tilde {\underline {\theta }}^n)$
that ends in
$(\tilde {\underline {\theta }}^1,\ldots ,\tilde {\underline {\theta }}^n)$
that ends in
![]() $(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
.
$(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
.
Using Proposition 3.3, we obtain a set
![]() $T\subset F$
such that
$T\subset F$
such that
 $$ \begin{align*}&Dh(x_0)\circ \pi_{\tilde{\underline{\theta}}^1,\ldots,\tilde{\underline{\theta}}^n,s'}(Q_1) \cap Dh(x_0)\circ \pi_{\tilde{\underline{\theta}}^1,\ldots,\tilde{\underline{\theta}}^n,s'}(Q_2)= \emptyset\\ &\qquad\text{for all } Q_1,Q_2\in T,\quad Q_1\neq Q_2,\end{align*} $$
$$ \begin{align*}&Dh(x_0)\circ \pi_{\tilde{\underline{\theta}}^1,\ldots,\tilde{\underline{\theta}}^n,s'}(Q_1) \cap Dh(x_0)\circ \pi_{\tilde{\underline{\theta}}^1,\ldots,\tilde{\underline{\theta}}^n,s'}(Q_2)= \emptyset\\ &\qquad\text{for all } Q_1,Q_2\in T,\quad Q_1\neq Q_2,\end{align*} $$
and
![]() $\#T\geq (c_3^2/(4a))\rho _1^{-(d_1+\cdots +d_n)}$
.
$\#T\geq (c_3^2/(4a))\rho _1^{-(d_1+\cdots +d_n)}$
.
We want to use Lemma 3.4 for
![]() $\phi =Dh(x_0)\circ \pi _{\tilde {\underline {\theta }}^1,\ldots ,\tilde {\underline {\theta }}^n,s'}$
,
$\phi =Dh(x_0)\circ \pi _{\tilde {\underline {\theta }}^1,\ldots ,\tilde {\underline {\theta }}^n,s'}$
,
![]() $\psi =L\circ h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
, where L is some affine function, and the set T. Note first that
$\psi =L\circ h\circ (f_{\underline {a}^1},\ldots ,f_{\underline {a}^n})$
, where L is some affine function, and the set T. Note first that
![]() $\underline {\theta }^j\wedge \tilde {\underline {\theta }}^j\in \Sigma _j(c_0,\rho _1)$
,
$\underline {\theta }^j\wedge \tilde {\underline {\theta }}^j\in \Sigma _j(c_0,\rho _1)$
,
![]() $1\leq j \leq n$
, since both
$1\leq j \leq n$
, since both
![]() $\underline {\theta }^j$
and
$\underline {\theta }^j$
and
![]() $\tilde {\underline {\theta }}^j$
end in
$\tilde {\underline {\theta }}^j$
end in
![]() $\tilde {\underline {a}}^j$
. Equation (4) implies then
$\tilde {\underline {a}}^j$
. Equation (4) implies then
However, item (ii) together with items (c) and (d) imply
We conclude
which together with equation (3) shows that we can use Lemma 3.4. Hence, there is a subset
![]() $T'(p)\subset T\subset F$
such that
$T'(p)\subset T\subset F$
such that
 $$ \begin{align*} &h\circ (f_{\underline{a}^1},\ldots,f_{\underline{a}^n})(Q_1)\cap h\circ (f_{\underline{a}^1},\ldots,f_{\underline{a}^n})(Q_1) = \emptyset\\ &\qquad\text{for all } Q_1,Q_2 \in T'(p), Q_1\neq Q_2,\end{align*} $$
$$ \begin{align*} &h\circ (f_{\underline{a}^1},\ldots,f_{\underline{a}^n})(Q_1)\cap h\circ (f_{\underline{a}^1},\ldots,f_{\underline{a}^n})(Q_1) = \emptyset\\ &\qquad\text{for all } Q_1,Q_2 \in T'(p), Q_1\neq Q_2,\end{align*} $$
and
 $$ \begin{align*}\#T'(p)\geq [3L(L+\tau)]^{-l}\cdot\frac{c_3^2}{4a}\rho_1^{-(d_1+\cdots+d_n)}\geq C_3^{-1}\rho_1^{\eta-(d_1+\cdots+d_n)}.\end{align*} $$
$$ \begin{align*}\#T'(p)\geq [3L(L+\tau)]^{-l}\cdot\frac{c_3^2}{4a}\rho_1^{-(d_1+\cdots+d_n)}\geq C_3^{-1}\rho_1^{\eta-(d_1+\cdots+d_n)}.\end{align*} $$
In the way we have defined
![]() $T'(p)$
, it clearly verifies items (iii), (iv), and (v).
$T'(p)$
, it clearly verifies items (iii), (iv), and (v).
Given
![]() $p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
, the children of p are defined by
$p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
, the children of p are defined by
The children of p clearly satisfy items (i) and (ii).
Now that we have defined N, we can finish the proof. For each non-negative integer k, consider the set
![]() $I(k)$
of elements
$I(k)$
of elements
![]() $p\in N$
generated in the k-step of the inductive process. (They are children of elements generated in the
$p\in N$
generated in the k-step of the inductive process. (They are children of elements generated in the
![]() $(k-1)$
-step, and the only element in the 0-step is
$(k-1)$
-step, and the only element in the 0-step is
![]() $p_0$
.) For each
$p_0$
.) For each
![]() $p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
, define the set
$p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
, define the set
We clearly have
 $$ \begin{align*}\bigcap_{k\geq 0}\bigcup_{p\in I(k)}G(p)\subset h(K_1\times\cdots\times K_n).\end{align*} $$
$$ \begin{align*}\bigcap_{k\geq 0}\bigcup_{p\in I(k)}G(p)\subset h(K_1\times\cdots\times K_n).\end{align*} $$
The desired result,
![]() $HD(h(K_1\times \cdots \times K_n))\geq d_1+\cdots +d_n-\eta $
, follows from Corollary 2.1 if we can prove that
$HD(h(K_1\times \cdots \times K_n))\geq d_1+\cdots +d_n-\eta $
, follows from Corollary 2.1 if we can prove that
 $$ \begin{align*}\sum_{q\in Ch(p)} \bigg(\frac{\mathrm{diam}(G(q))}{\mathrm{diam} (G(p))}\bigg)^{d_1+\cdots+d_n-\eta}\geq 1,\end{align*} $$
$$ \begin{align*}\sum_{q\in Ch(p)} \bigg(\frac{\mathrm{diam}(G(q))}{\mathrm{diam} (G(p))}\bigg)^{d_1+\cdots+d_n-\eta}\geq 1,\end{align*} $$
and each set
![]() $G(p)$
contains a ball with radius proportional to its diameter. All other requirements in the corollary are obviously verified.
$G(p)$
contains a ball with radius proportional to its diameter. All other requirements in the corollary are obviously verified.
Given
![]() $p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
, properties (i), (ii) and the observation in property (c) imply that
$p=(\underline {a}^1,\ldots ,\underline {a}^n,\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in N$
, properties (i), (ii) and the observation in property (c) imply that
![]() $s\in J_r$
and
$s\in J_r$
and
![]() $s(\underline {a}^1,\ldots ,\underline {a}^n):=(\log ({r_{\underline {a}^1}}/{r_{\underline {a}^n}}),\ldots ,\log ({r_{\underline {a}^{n-1}}}/{r_{\underline {a}^n}}), v_{\underline {a}^1},\ldots , v_{\underline {a}^n})$
is very close to s. Thus, we can assume
$s(\underline {a}^1,\ldots ,\underline {a}^n):=(\log ({r_{\underline {a}^1}}/{r_{\underline {a}^n}}),\ldots ,\log ({r_{\underline {a}^{n-1}}}/{r_{\underline {a}^n}}), v_{\underline {a}^1},\ldots , v_{\underline {a}^n})$
is very close to s. Thus, we can assume
![]() $s(\underline {a}^1,\ldots ,\underline {a}^n)\in J_{2r}$
and then we can think of
$s(\underline {a}^1,\ldots ,\underline {a}^n)\in J_{2r}$
and then we can think of
![]() $G(\underline {a}^1)\times \cdots \times G(\underline {a}^n)$
as being a square; indeed we have
$G(\underline {a}^1)\times \cdots \times G(\underline {a}^n)$
as being a square; indeed we have
![]() $\mathrm { diam}(G(\underline {a}^j))\leq e^{4r} \mathrm {diam}(G(\underline {a}^m))$
for any
$\mathrm { diam}(G(\underline {a}^j))\leq e^{4r} \mathrm {diam}(G(\underline {a}^m))$
for any
![]() $j, m$
. This together with the fact that
$j, m$
. This together with the fact that
![]() $Dh(x_0)$
verify that the transversality hypotheses allow us to conclude that
$Dh(x_0)$
verify that the transversality hypotheses allow us to conclude that
![]() $h(G(\underline {a}^1)\times \cdots \times G(\underline {a}^n))$
contains a ball with radius proportional to its diameter. Moreover,
$h(G(\underline {a}^1)\times \cdots \times G(\underline {a}^n))$
contains a ball with radius proportional to its diameter. Moreover,
 $$ \begin{align*} (C_3')^{-1} \mathrm{diam}(G(\underline{a}^1)\times\cdots\times G(\underline{a}^n)) &\leq \mathrm{diam}(h(G(\underline{a}^1)\times\cdots\times G(\underline{a}^n)))\\ &\leq C_3' \mathrm{diam}(G(\underline{a}^1)\times\cdots\times G(\underline{a}^n)) \end{align*} $$
$$ \begin{align*} (C_3')^{-1} \mathrm{diam}(G(\underline{a}^1)\times\cdots\times G(\underline{a}^n)) &\leq \mathrm{diam}(h(G(\underline{a}^1)\times\cdots\times G(\underline{a}^n)))\\ &\leq C_3' \mathrm{diam}(G(\underline{a}^1)\times\cdots\times G(\underline{a}^n)) \end{align*} $$
for a constant
![]() $C_3'>0$
, depending only on r, h, and the Cantor sets. However, we can choose
$C_3'>0$
, depending only on r, h, and the Cantor sets. However, we can choose
![]() $C_4'>0$
, independent of
$C_4'>0$
, independent of
![]() $\rho $
, such that
$\rho $
, such that
![]() $\mathrm {diam}(G(\underline {a}\underline {b}))\geq C^{\prime }_4 \rho \cdot \mathrm {diam} (G(\underline {a}))$
for any
$\mathrm {diam}(G(\underline {a}\underline {b}))\geq C^{\prime }_4 \rho \cdot \mathrm {diam} (G(\underline {a}))$
for any
![]() $\underline {a}\in \Sigma _j^\textit{fin}$
and
$\underline {a}\in \Sigma _j^\textit{fin}$
and
![]() $\underline {b}\in \Sigma _j(c_0,\rho )$
,
$\underline {b}\in \Sigma _j(c_0,\rho )$
,
![]() $0 \leq j\leq n$
. Therefore, we can choose
$0 \leq j\leq n$
. Therefore, we can choose
![]() $C_3>0$
that does not depend on
$C_3>0$
that does not depend on
![]() $\rho _1$
, such that
$\rho _1$
, such that
 $$ \begin{align} \bigg(\frac{\mathrm{diam}(G(q))}{\mathrm{diam} (G(p))}\bigg)^{d_1+\cdots+d_n-\eta}\geq C_3 \rho_1^{d_1+\cdots+d_n-\eta} \end{align} $$
$$ \begin{align} \bigg(\frac{\mathrm{diam}(G(q))}{\mathrm{diam} (G(p))}\bigg)^{d_1+\cdots+d_n-\eta}\geq C_3 \rho_1^{d_1+\cdots+d_n-\eta} \end{align} $$
for any
![]() $q\in Ch(p)$
. Now that
$q\in Ch(p)$
. Now that
![]() $C_3$
has been chosen, we get
$C_3$
has been chosen, we get
 $$ \begin{align*}\sum_{q\in Ch(p)} \bigg(\frac{\mathrm{diam}(G(q))}{\mathrm{diam} (G(p))}\bigg)^{d_1+\cdots+d_n-\eta}&\geq \sum_{q\in Ch(p)} C_3 \rho_1^{d_1+\cdots+d_n-\eta}\\&= C_3 \rho_1^{d_1+\cdots+d_n-\eta}\cdot \#T'(p)\geq 1.\\[-3.1pc]\end{align*} $$
$$ \begin{align*}\sum_{q\in Ch(p)} \bigg(\frac{\mathrm{diam}(G(q))}{\mathrm{diam} (G(p))}\bigg)^{d_1+\cdots+d_n-\eta}&\geq \sum_{q\in Ch(p)} C_3 \rho_1^{d_1+\cdots+d_n-\eta}\\&= C_3 \rho_1^{d_1+\cdots+d_n-\eta}\cdot \#T'(p)\geq 1.\\[-3.1pc]\end{align*} $$
Theorem B. (Dimension formula)
Let
![]() $K_1,\ldots ,K_n$
be
$K_1,\ldots ,K_n$
be
![]() $C^m$
,
$C^m$
,
![]() $m\geq 2$
, conformal regular Cantor sets generated by expanding maps
$m\geq 2$
, conformal regular Cantor sets generated by expanding maps
![]() $g_1,\ldots ,g_n$
, respectively. Suppose all of them are not essentially affine. Assume that there exist periodic points
$g_1,\ldots ,g_n$
, respectively. Suppose all of them are not essentially affine. Assume that there exist periodic points
![]() $p_j \in K_j$
, with period
$p_j \in K_j$
, with period
![]() $n_j$
for
$n_j$
for
![]() $1\leq j\leq n$
, such that if we write
$1\leq j\leq n$
, such that if we write
![]() $Dg_j^{n_j}(p_j)=\frac {1}{r_j} R_{-v_j},$
where
$Dg_j^{n_j}(p_j)=\frac {1}{r_j} R_{-v_j},$
where
![]() $R_v$
is the rotation matrix by an angle
$R_v$
is the rotation matrix by an angle
![]() $v\in \mathbb {T}$
, then
$v\in \mathbb {T}$
, then
 $$ \begin{align*} (\log r_1,0,\ldots,0&;v_1,0,\ldots,0),\\ &\vdots \\ (0,\ldots,\log r_{n-1}&;0,\ldots,v_{n-1},0),\\ (-\log r_n,\ldots,-\log r_n &;0,\ldots,0,v_n) \end{align*} $$
$$ \begin{align*} (\log r_1,0,\ldots,0&;v_1,0,\ldots,0),\\ &\vdots \\ (0,\ldots,\log r_{n-1}&;0,\ldots,v_{n-1},0),\\ (-\log r_n,\ldots,-\log r_n &;0,\ldots,0,v_n) \end{align*} $$
generate a dense subgroup of J. Let h be any
![]() $C^{1}$
function defined on a neighborhood of
$C^{1}$
function defined on a neighborhood of
![]() $K_1\times \cdots \times K_n$
into
$K_1\times \cdots \times K_n$
into
![]() $\mathbb {R}^l$
such that there exists a point
$\mathbb {R}^l$
such that there exists a point
![]() $x_0\in K_1\times \cdots \times K_n$
where
$x_0\in K_1\times \cdots \times K_n$
where
![]() $Dh(x_0)$
verifies the transversality hypotheses, then
$Dh(x_0)$
verifies the transversality hypotheses, then
Proof. We first treat the case
![]() $HD(K_1)+\cdots +HD(K_n)<l$
. Notice that
$HD(K_1)+\cdots +HD(K_n)<l$
. Notice that
![]() $K_1,\ldots ,K_n$
verify the hypotheses of the scale recurrence lemma; the existence of the periodic points
$K_1,\ldots ,K_n$
verify the hypotheses of the scale recurrence lemma; the existence of the periodic points
![]() $p_j$
imply that all of the Cantor sets are not essentially real. The desired result follows from the preceding theorem if we show that for any
$p_j$
imply that all of the Cantor sets are not essentially real. The desired result follows from the preceding theorem if we show that for any
![]() $(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in \Sigma _1^-\times \cdots \times \Sigma _n^-\times J_r$
, there exists
$(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)\in \Sigma _1^-\times \cdots \times \Sigma _n^-\times J_r$
, there exists
![]() $(\underline {c}^1,\ldots ,\underline {c}^n)\in \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}$
such that
$(\underline {c}^1,\ldots ,\underline {c}^n)\in \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}$
such that
![]() $T_{\underline {c}^1,\ldots ,\underline {c}^n}(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)=(\underline {\theta }^1\underline {c}^1,\ldots ,\underline {\theta }^n\underline {c}^n,\tilde {s})$
and
$T_{\underline {c}^1,\ldots ,\underline {c}^n}(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)=(\underline {\theta }^1\underline {c}^1,\ldots ,\underline {\theta }^n\underline {c}^n,\tilde {s})$
and
![]() $\tilde {s}\in F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for some
$\tilde {s}\in F^*(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for some
![]() $(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for which
$(\tilde {\underline {a}}^1,\ldots ,\tilde {\underline {a}}^n)$
for which
![]() $(\underline {\theta }^1\underline {c}^1,\ldots ,\underline {\theta }^n\underline {c}^n)$
ends in it.
$(\underline {\theta }^1\underline {c}^1,\ldots ,\underline {\theta }^n\underline {c}^n)$
ends in it.
Let
![]() $\underline {a}_j \in \Sigma _j^\textit{fin}$
be the word of length
$\underline {a}_j \in \Sigma _j^\textit{fin}$
be the word of length
![]() $n_j$
such that the periodic point
$n_j$
such that the periodic point
![]() $p_j$
corresponds to the sequence
$p_j$
corresponds to the sequence
![]() $\underline {a}_j \underline {a}_j \underline {a}_j\cdots $
. For a finite sequence
$\underline {a}_j \underline {a}_j \underline {a}_j\cdots $
. For a finite sequence
![]() $\underline {a}\in \Sigma _j^\textit{fin}$
and
$\underline {a}\in \Sigma _j^\textit{fin}$
and
![]() $k\in \mathbb {Z}^+$
, we are going to use the notation
$k\in \mathbb {Z}^+$
, we are going to use the notation
 $\underline {a}^k=\underbrace {\underline {a} \underline {a}\cdots \underline {a}}_{k-times}.$
$\underline {a}^k=\underbrace {\underline {a} \underline {a}\cdots \underline {a}}_{k-times}.$
Choosing
![]() $c_0$
big enough and assuming
$c_0$
big enough and assuming
![]() $\rho $
is small, we can find
$\rho $
is small, we can find
![]() $k_j\in \mathbb {Z}^+$
such that
$k_j\in \mathbb {Z}^+$
such that
![]() $\tilde {\underline {a}}_j:=\underline {a}_j^{k_j} \in \Sigma _j(c_0,\rho ).$
Define
$\tilde {\underline {a}}_j:=\underline {a}_j^{k_j} \in \Sigma _j(c_0,\rho ).$
Define
![]() $\underline {\theta }_j=\cdots \tilde {\underline {a}}_j\cdots \tilde {\underline {a}}_j\in \Sigma _j^-.$
$\underline {\theta }_j=\cdots \tilde {\underline {a}}_j\cdots \tilde {\underline {a}}_j\in \Sigma _j^-.$
By properties (ii) and (iii) of the scale recurrence lemma, we know that there are
![]() $s_0, s_1 \in J$
,
$s_0, s_1 \in J$
,
![]() $\underline {b}_j\in \Sigma _j(c_0,\rho )$
and
$\underline {b}_j\in \Sigma _j(c_0,\rho )$
and
![]() $\underline {c}_j \in \Sigma ^\textit{fin}_j$
,
$\underline {c}_j \in \Sigma ^\textit{fin}_j$
,
![]() $1\leq j \leq n$
, such that
$1\leq j \leq n$
, such that
![]() $T_{\underline {c}_1\underline {b}_1,\ldots ,\underline {c}_n\underline {b}_n}(\underline {\theta }_1,\ldots ,\underline {\theta }_n,s_0)=(\underline {\theta }_1\underline {c}_1\underline {b}_1,\ldots ,\underline {\theta }_n\underline {c}_n\underline {b}_n,s_1),$
and the
$T_{\underline {c}_1\underline {b}_1,\ldots ,\underline {c}_n\underline {b}_n}(\underline {\theta }_1,\ldots ,\underline {\theta }_n,s_0)=(\underline {\theta }_1\underline {c}_1\underline {b}_1,\ldots ,\underline {\theta }_n\underline {c}_n\underline {b}_n,s_1),$
and the
![]() $\rho $
-neighborhood of
$\rho $
-neighborhood of
![]() $s_1$
is contained in
$s_1$
is contained in
![]() $F^*(\underline {b}_1,\ldots ,\underline {b}_n)$
.
$F^*(\underline {b}_1,\ldots ,\underline {b}_n)$
.
Thanks to the continuity of the map
![]() $\underline {\theta }\to k^{\underline {\theta }}$
, we can choose positive integers
$\underline {\theta }\to k^{\underline {\theta }}$
, we can choose positive integers
![]() $l_1,\ldots ,l_n$
, depending on
$l_1,\ldots ,l_n$
, depending on
![]() $\rho $
, such that for any
$\rho $
, such that for any
![]() $m_j>l_j$
, any
$m_j>l_j$
, any
![]() $\underline {\theta }^j \in \Sigma _j^-$
,
$\underline {\theta }^j \in \Sigma _j^-$
,
![]() $1\leq j\leq n$
, and x in the
$1\leq j\leq n$
, and x in the
![]() $\rho /2$
-neighborhood of
$\rho /2$
-neighborhood of
![]() $s_0$
, we have
$s_0$
, we have
and
![]() $\tilde {x} \in F^*(\underline {b}_1,\ldots ,\underline {b}_n)$
. (We assume
$\tilde {x} \in F^*(\underline {b}_1,\ldots ,\underline {b}_n)$
. (We assume
![]() $\underline {\theta }^j$
,
$\underline {\theta }^j$
,
![]() $1\leq j \leq n$
, ends with the letters in which
$1\leq j \leq n$
, ends with the letters in which
![]() $\underline {a}_j$
,
$\underline {a}_j$
,
![]() $1\leq j \leq n$
, starts, otherwise we consider
$1\leq j \leq n$
, starts, otherwise we consider
![]() $\underline {d}^j\tilde {\underline {a}}_j^m$
instead of
$\underline {d}^j\tilde {\underline {a}}_j^m$
instead of
![]() $\tilde {\underline {a}}_j^m$
for some
$\tilde {\underline {a}}_j^m$
for some
![]() $\underline {d}^j$
, and the proof follows in the same way.)
$\underline {d}^j$
, and the proof follows in the same way.)
Now notice that
![]() $r^{\underline {\theta }^j}_{\tilde {\underline {a}}^{l_j+m_j}}=r^{\underline {\theta }^j}_{\tilde {\underline {a}}^{l_j}}\cdot r^{\underline {\theta }^j\tilde {\underline {a}}^{l_j}}_{\tilde {\underline {a}}^{m_j}},$
and if
$r^{\underline {\theta }^j}_{\tilde {\underline {a}}^{l_j+m_j}}=r^{\underline {\theta }^j}_{\tilde {\underline {a}}^{l_j}}\cdot r^{\underline {\theta }^j\tilde {\underline {a}}^{l_j}}_{\tilde {\underline {a}}^{m_j}},$
and if
![]() $l_j$
is big enough, we have
$l_j$
is big enough, we have
 $$ \begin{align*}\Big|\log r^{\underline{\theta}^j\tilde{\underline{a}}_j^{l_j}}_{\tilde{\underline{a}}_j^{m_j}}-\log r^{\underline{\theta}_j}_{\tilde{\underline{a}}_j^{m_j}}\Big|<\frac{\rho}{8(2n-1)}\end{align*} $$
$$ \begin{align*}\Big|\log r^{\underline{\theta}^j\tilde{\underline{a}}_j^{l_j}}_{\tilde{\underline{a}}_j^{m_j}}-\log r^{\underline{\theta}_j}_{\tilde{\underline{a}}_j^{m_j}}\Big|<\frac{\rho}{8(2n-1)}\end{align*} $$
for any
![]() $m_j\in \mathbb {Z}^+$
. Similar formulas hold for
$m_j\in \mathbb {Z}^+$
. Similar formulas hold for
![]() $v^{\underline {\theta }^j\tilde {\underline {a}}_j^{l_j}}_{\tilde {\underline {a}}_j^{m_j}}$
.
$v^{\underline {\theta }^j\tilde {\underline {a}}_j^{l_j}}_{\tilde {\underline {a}}_j^{m_j}}$
.
For
![]() $m_j\in \mathbb {Z}^+$
,
$m_j\in \mathbb {Z}^+$
,
![]() $1\leq j\leq n$
, consider
$1\leq j\leq n$
, consider
![]() $T_{\tilde {\underline {a}}_1^{l_1+m_1},\ldots ,\tilde {\underline {a}}_j^{l_j+m_j}}(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)=(\tilde {\underline {\theta }}^1,\ldots ,\tilde {\underline {\theta }}^n,\tilde {s}).$
We have
$T_{\tilde {\underline {a}}_1^{l_1+m_1},\ldots ,\tilde {\underline {a}}_j^{l_j+m_j}}(\underline {\theta }^1,\ldots ,\underline {\theta }^n,s)=(\tilde {\underline {\theta }}^1,\ldots ,\tilde {\underline {\theta }}^n,\tilde {s}).$
We have
 $$ \begin{align*} \tilde{s}&=s+\Big(\!\log r_{\tilde{\underline{a}}_1^{l_1+m_1}}^{\underline{\theta}^1}-\log r_{\tilde{\underline{a}}_n^{l_n+m_n}}^{\underline{\theta}^n},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{l_{n-1}+m_{n-1}}}^{\underline{\theta}^{n-1}}-\log r_{\tilde{\underline{a}}_n^{l_n+m_n}}^{\underline{\theta}^n};v_{\tilde{\underline{a}}_1^{l_1+m_1}}^{\underline{\theta}^1},\ldots,v_{\tilde{\underline{a}}_n^{l_n+m_n}}^{\underline{\theta}^n}\!\Big)\\ &=s+\Big(\!\log r_{\tilde{\underline{a}}_1^{l_1}}^{\underline{\theta}^1}-\log r_{\tilde{\underline{a}}_n^{l_n}}^{\underline{\theta}^n},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{l_{n-1}}}^{\underline{\theta}^{n-1}}-\log r_{\tilde{\underline{a}}_n^{l_n}}^{\underline{\theta}^n};v_{\tilde{\underline{a}}_1^{l_1}}^{\underline{\theta}^1},\ldots,v_{\tilde{\underline{a}}_n^{l_n}}^{\underline{\theta}^n}\!\Big)\\ &\quad+\Big(\!\log r_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}^1\tilde{\underline{a}}_1^{l_1}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{m_{n-1}}}^{\underline{\theta}^{n-1}\tilde{\underline{a}}_{n-1}^{l_{n-1}}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}};v_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}^1\tilde{\underline{a}}_1^{l_1}},\ldots,v_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}}\!\Big). \end{align*} $$
$$ \begin{align*} \tilde{s}&=s+\Big(\!\log r_{\tilde{\underline{a}}_1^{l_1+m_1}}^{\underline{\theta}^1}-\log r_{\tilde{\underline{a}}_n^{l_n+m_n}}^{\underline{\theta}^n},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{l_{n-1}+m_{n-1}}}^{\underline{\theta}^{n-1}}-\log r_{\tilde{\underline{a}}_n^{l_n+m_n}}^{\underline{\theta}^n};v_{\tilde{\underline{a}}_1^{l_1+m_1}}^{\underline{\theta}^1},\ldots,v_{\tilde{\underline{a}}_n^{l_n+m_n}}^{\underline{\theta}^n}\!\Big)\\ &=s+\Big(\!\log r_{\tilde{\underline{a}}_1^{l_1}}^{\underline{\theta}^1}-\log r_{\tilde{\underline{a}}_n^{l_n}}^{\underline{\theta}^n},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{l_{n-1}}}^{\underline{\theta}^{n-1}}-\log r_{\tilde{\underline{a}}_n^{l_n}}^{\underline{\theta}^n};v_{\tilde{\underline{a}}_1^{l_1}}^{\underline{\theta}^1},\ldots,v_{\tilde{\underline{a}}_n^{l_n}}^{\underline{\theta}^n}\!\Big)\\ &\quad+\Big(\!\log r_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}^1\tilde{\underline{a}}_1^{l_1}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{m_{n-1}}}^{\underline{\theta}^{n-1}\tilde{\underline{a}}_{n-1}^{l_{n-1}}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}};v_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}^1\tilde{\underline{a}}_1^{l_1}},\ldots,v_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}}\!\Big). \end{align*} $$
Now notice that
 $$ \begin{align*}\Big(\log r_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}^1\tilde{\underline{a}}_1^{l_1}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{m_{n-1}}}^{\underline{\theta}^{n-1}\tilde{\underline{a}}_{n-1}^{l_{n-1}}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}};v_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}^1\tilde{\underline{a}}_1^{l_1}},\ldots,v_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}}\Big)\end{align*} $$
$$ \begin{align*}\Big(\log r_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}^1\tilde{\underline{a}}_1^{l_1}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{m_{n-1}}}^{\underline{\theta}^{n-1}\tilde{\underline{a}}_{n-1}^{l_{n-1}}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}};v_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}^1\tilde{\underline{a}}_1^{l_1}},\ldots,v_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}^n\tilde{\underline{a}}_n^{l_n}}\Big)\end{align*} $$
is in the
![]() $\rho /4$
neighborhood of
$\rho /4$
neighborhood of
However,
 $$ \begin{align*} &\Big(\log r_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}_1}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}_n},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{m_{n-1}}}^{\underline{\theta}_{n-1}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}_n};v_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}_1},\ldots,v_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}_n}\Big)\\ &\quad= m_1 \Big(\log r_{\tilde{\underline{a}}_1}^{\underline{\theta}_1},0,\ldots,0;v_{\tilde{\underline{a}}_1}^{\underline{\theta}_1},0,\ldots,0\Big)\\&\qquad+\cdots+ m_{n-1}\Big(0,\ldots,\log r_{\tilde{\underline{a}}_{n-1}}^{\underline{\theta}_{n-1}};0,\ldots,v_{\tilde{\underline{a}}_{n-1}}^{\underline{\theta}_{n-1}},0\Big)\\ &\qquad+m_n\Big(-\log r_{\tilde{\underline{a}}_{n}}^{\underline{\theta}_{n}},\ldots,-\log r_{\tilde{\underline{a}}_{n}}^{\underline{\theta}_{n}};0,\ldots,0,v_{\tilde{\underline{a}}_{n}}^{\underline{\theta}_{n}}\Big). \end{align*} $$
$$ \begin{align*} &\Big(\log r_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}_1}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}_n},\ldots, \log r_{\tilde{\underline{a}}_{n-1}^{m_{n-1}}}^{\underline{\theta}_{n-1}}-\log r_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}_n};v_{\tilde{\underline{a}}_1^{m_1}}^{\underline{\theta}_1},\ldots,v_{\tilde{\underline{a}}_n^{m_n}}^{\underline{\theta}_n}\Big)\\ &\quad= m_1 \Big(\log r_{\tilde{\underline{a}}_1}^{\underline{\theta}_1},0,\ldots,0;v_{\tilde{\underline{a}}_1}^{\underline{\theta}_1},0,\ldots,0\Big)\\&\qquad+\cdots+ m_{n-1}\Big(0,\ldots,\log r_{\tilde{\underline{a}}_{n-1}}^{\underline{\theta}_{n-1}};0,\ldots,v_{\tilde{\underline{a}}_{n-1}}^{\underline{\theta}_{n-1}},0\Big)\\ &\qquad+m_n\Big(-\log r_{\tilde{\underline{a}}_{n}}^{\underline{\theta}_{n}},\ldots,-\log r_{\tilde{\underline{a}}_{n}}^{\underline{\theta}_{n}};0,\ldots,0,v_{\tilde{\underline{a}}_{n}}^{\underline{\theta}_{n}}\Big). \end{align*} $$
Moreover,
 $r_{\tilde {\underline {a}}_j}^{\underline {\theta }_j} R_{v_{\tilde {\underline {a}}_j}^{\underline {\theta }_j}}=[Dg^{k_jn_j}(p_j)]^{-1}=r_j^{k_j}R_{k_jv_j}.$
Therefore, the density hypothesis in the theorem, together with the next lemma, implies that there exist
$r_{\tilde {\underline {a}}_j}^{\underline {\theta }_j} R_{v_{\tilde {\underline {a}}_j}^{\underline {\theta }_j}}=[Dg^{k_jn_j}(p_j)]^{-1}=r_j^{k_j}R_{k_jv_j}.$
Therefore, the density hypothesis in the theorem, together with the next lemma, implies that there exist
![]() $m_1,\ldots ,m_n \in \mathbb {Z}^+$
such that
$m_1,\ldots ,m_n \in \mathbb {Z}^+$
such that
is in the
![]() $\rho /4$
-neighborhood of
$\rho /4$
-neighborhood of
Hence,
![]() $\tilde {s}$
is in the
$\tilde {s}$
is in the
![]() $\rho /2$
-neighborhood of
$\rho /2$
-neighborhood of
![]() $s_0$
and from this, we get
$s_0$
and from this, we get
 $$ \begin{align*} T_{\tilde{\underline{a}}_1^{l_1+m_1}\underline{c}_1\underline{b}_1,\ldots,\tilde{\underline{a}}_n^{l_n+m_n}\underline{c}_n\underline{b}_n}(\underline{\theta}^1,\ldots,\underline{\theta}^n,s)&= T_{\underline{c}_1\underline{b}_1,\ldots,\underline{c}_n\underline{b}_n}(\underline{\theta}^1\tilde{\underline{a}}_1^{l_1+m_1},\ldots,\underline{\theta}^n\tilde{\underline{a}}_n^{l_n+m_n},\tilde{s})\\ &=(\underline{\theta}^1\tilde{\underline{a}}_1^{l_1+m_1}\underline{c}_1\underline{b}_1,\ldots,\underline{\theta}^n\tilde{\underline{a}}_n^{l_n+m_n}\underline{c}_n\underline{b}_n,\tilde{s}'), \end{align*} $$
$$ \begin{align*} T_{\tilde{\underline{a}}_1^{l_1+m_1}\underline{c}_1\underline{b}_1,\ldots,\tilde{\underline{a}}_n^{l_n+m_n}\underline{c}_n\underline{b}_n}(\underline{\theta}^1,\ldots,\underline{\theta}^n,s)&= T_{\underline{c}_1\underline{b}_1,\ldots,\underline{c}_n\underline{b}_n}(\underline{\theta}^1\tilde{\underline{a}}_1^{l_1+m_1},\ldots,\underline{\theta}^n\tilde{\underline{a}}_n^{l_n+m_n},\tilde{s})\\ &=(\underline{\theta}^1\tilde{\underline{a}}_1^{l_1+m_1}\underline{c}_1\underline{b}_1,\ldots,\underline{\theta}^n\tilde{\underline{a}}_n^{l_n+m_n}\underline{c}_n\underline{b}_n,\tilde{s}'), \end{align*} $$
and
![]() $\tilde {s}'\in F^*(\underline {b}_1,\ldots ,\underline {b}_n)$
, as we wanted.
$\tilde {s}'\in F^*(\underline {b}_1,\ldots ,\underline {b}_n)$
, as we wanted.
If
![]() $HD(K_1)+\cdots +HD(K_n)\geq l$
, fix
$HD(K_1)+\cdots +HD(K_n)\geq l$
, fix
![]() $\epsilon>0$
and find conformal regular Cantor sets
$\epsilon>0$
and find conformal regular Cantor sets
![]() $\tilde {K}_j\subset K_j$
,
$\tilde {K}_j\subset K_j$
,
![]() $1\leq j\leq n$
such that
$1\leq j\leq n$
such that
![]() $l-\epsilon <HD(\tilde {K}_1)+\cdots +HD(\tilde {K}_n)<l$
,
$l-\epsilon <HD(\tilde {K}_1)+\cdots +HD(\tilde {K}_n)<l$
,
![]() $p_j\in \tilde {K}_j$
, and the expanding map of
$p_j\in \tilde {K}_j$
, and the expanding map of
![]() $\tilde {K}_j$
is given by a power of
$\tilde {K}_j$
is given by a power of
![]() $g_j$
,
$g_j$
,
![]() $1\leq j \leq n$
(see [Reference Moreira8, Lemma in p. 16]). We get
$1\leq j \leq n$
(see [Reference Moreira8, Lemma in p. 16]). We get
 $$ \begin{align*} l\geq HD(h(K_1\times \cdots\times K_n))&\geq HD(h(\tilde{K}_1 \times\cdots\times \tilde{K}_n))\\ &=HD(\tilde{K}_1)+\cdots+HD(\tilde{K}_n)>l-\epsilon. \end{align*} $$
$$ \begin{align*} l\geq HD(h(K_1\times \cdots\times K_n))&\geq HD(h(\tilde{K}_1 \times\cdots\times \tilde{K}_n))\\ &=HD(\tilde{K}_1)+\cdots+HD(\tilde{K}_n)>l-\epsilon. \end{align*} $$
Since
![]() $\epsilon $
can be arbitrarily small, we obtain
$\epsilon $
can be arbitrarily small, we obtain
![]() $HD(h(K\times \cdots \times K_n))=l$
as we wanted.
$HD(h(K\times \cdots \times K_n))=l$
as we wanted.
The following lemma was used in the previous theorem. It also implies that the hypothesis needed for the dimension formula is generic. Its proof is based on the well-known Kronecker theorem.
Lemma 3.5. Let
![]() $\unicode{x3bb} _j<0$
,
$\unicode{x3bb} _j<0$
,
![]() $v_j\in \mathbb {T}$
,
$v_j\in \mathbb {T}$
,
![]() $1\leq j\leq n$
, and consider the set
$1\leq j\leq n$
, and consider the set
![]() $E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots, v_n)\subset \mathbb {R}^{n-1}\times \mathbb {T}^{n}$
given by the vectors
$E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots, v_n)\subset \mathbb {R}^{n-1}\times \mathbb {T}^{n}$
given by the vectors

We have the following properties.
-
(a) If
 $E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)$
generates a dense subgroup of
$E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)$
generates a dense subgroup of
 $\mathbb {R}^{n-1}\times \mathbb {T}^{n}$
, then
$\mathbb {R}^{n-1}\times \mathbb {T}^{n}$
, then
 $E(k_1 \unicode{x3bb} _1,\ldots ,k_n \unicode{x3bb} _n,k_1 v_1,\ldots ,k_n v_n)$
also generates a dense subgroup for all
$E(k_1 \unicode{x3bb} _1,\ldots ,k_n \unicode{x3bb} _n,k_1 v_1,\ldots ,k_n v_n)$
also generates a dense subgroup for all
 $k_1,\ldots ,k_n \in \mathbb {Z}\setminus \{0\}$
.
$k_1,\ldots ,k_n \in \mathbb {Z}\setminus \{0\}$
. -
(b) If
 $E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)$
generates a dense subgroup of
$E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)$
generates a dense subgroup of
 $\mathbb {R}^{n-1}\times \mathbb {T}^{n}$
, then it also generates a dense semigroup, that is, the set of linear combinations of vectors in
$\mathbb {R}^{n-1}\times \mathbb {T}^{n}$
, then it also generates a dense semigroup, that is, the set of linear combinations of vectors in
 $E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)$
with coefficients in
$E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)$
with coefficients in
 $\mathbb {N}$
is dense in
$\mathbb {N}$
is dense in
 $\mathbb {R}^{n-1}\times \mathbb {T}^{n}$
.
$\mathbb {R}^{n-1}\times \mathbb {T}^{n}$
. -
(c) The set of values
 $(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)\in \mathbb {R}_{<0}^{n}\times \mathbb {T}^n$
, for which the set
$(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)\in \mathbb {R}_{<0}^{n}\times \mathbb {T}^n$
, for which the set
 $E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)$
generates a dense subgroup, is a countable intersection of open and dense subsets.
$E(\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _n,v_1,\ldots ,v_n)$
generates a dense subgroup, is a countable intersection of open and dense subsets.
4 Proof of the scale recurrence lemma
In this section, we will present the proof of the scale recurrence lemma, it follows the ideas in [Reference Moreira and Yoccoz7] with some modifications. One of the main new features is the use of the not essentially real hypotheses. In §4.3, we use this hypothesis to estimate the norm
![]() $|x-y|$
from an inner product
$|x-y|$
from an inner product
![]() $\langle \xi , x-y \rangle $
, for some pairs x, y in a Cantor set. Roughly speaking, the not essentially real hypothesis allows us to choose many x, y such that the vector
$\langle \xi , x-y \rangle $
, for some pairs x, y in a Cantor set. Roughly speaking, the not essentially real hypothesis allows us to choose many x, y such that the vector
![]() $x-y$
is far from being orthogonal to
$x-y$
is far from being orthogonal to
![]() $\xi $
.
$\xi $
.
We also introduced new objects that were not present in the logical structure of [Reference Moreira and Yoccoz7]; there was a minor flaw in that paper, exactly in the proof of the scale recurrence lemma. We defined these objects to deal with this problem.
The flaw in [Reference Moreira and Yoccoz7] is in the proof of lemma 6.6, exactly in the part where one tries to estimate the measure of
![]() $\hat {\hat {E}}_n(\unicode{x3bb} )$
outside the interval
$\hat {\hat {E}}_n(\unicode{x3bb} )$
outside the interval
![]() $[-r+2\log c_0+\Delta _1\rho ,r-2\log c_0-\Delta _1\rho ]$
, which would correspond to estimating the measure of
$[-r+2\log c_0+\Delta _1\rho ,r-2\log c_0-\Delta _1\rho ]$
, which would correspond to estimating the measure of
![]() $\tilde {E}_m(\unicode{x3bb} )$
outside of
$\tilde {E}_m(\unicode{x3bb} )$
outside of
![]() $J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }$
in our paper. We considered, apart from the parameter
$J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }$
in our paper. We considered, apart from the parameter
![]() $c_0$
, another parameter
$c_0$
, another parameter
![]() $\tilde {c}_0$
, which is smaller than
$\tilde {c}_0$
, which is smaller than
![]() $c_0$
. We then created a statement, similar to the scale recurrence lemma, involving both parameters, the sets
$c_0$
. We then created a statement, similar to the scale recurrence lemma, involving both parameters, the sets
![]() $\Sigma _j(\tilde {c}_0,\rho )$
used to parameterize sets
$\Sigma _j(\tilde {c}_0,\rho )$
used to parameterize sets
![]() $E(\underline {a}^1,\ldots ,\underline {a}^n)$
and the sets
$E(\underline {a}^1,\ldots ,\underline {a}^n)$
and the sets
![]() $\Sigma _j(c_0,\rho )$
used to parameterize renormalization operators. We prove that the statement implies the original lemma. Finally, we prove the statement using an analogous logical structure to that presented in [Reference Moreira and Yoccoz7]. A similar approach can be used in [Reference Moreira and Yoccoz7].
$\Sigma _j(c_0,\rho )$
used to parameterize renormalization operators. We prove that the statement implies the original lemma. Finally, we prove the statement using an analogous logical structure to that presented in [Reference Moreira and Yoccoz7]. A similar approach can be used in [Reference Moreira and Yoccoz7].
4.1 General setting
We proceed as in [Reference Moreira and Yoccoz7, 6.1] using Fourier analysis in the group J instead of
![]() $\mathbb {R}$
. Let A be a set of indices,
$\mathbb {R}$
. Let A be a set of indices,
![]() $\Lambda $
a finite set, and maps
$\Lambda $
a finite set, and maps
![]() $\alpha :\Lambda \to A$
,
$\alpha :\Lambda \to A$
,
![]() $\omega :\Lambda \to A$
. Define
$\omega :\Lambda \to A$
. Define
![]() $\Lambda _i=\alpha ^{-1}(i)$
,
$\Lambda _i=\alpha ^{-1}(i)$
,
![]() $\Lambda ^j=\omega ^{-1}(j)$
,
$\Lambda ^j=\omega ^{-1}(j)$
,
![]() $\Lambda _i^j=\Lambda _i\cap \Lambda ^j$
,
$\Lambda _i^j=\Lambda _i\cap \Lambda ^j$
,
![]() $N_i=\#\Lambda _i$
,
$N_i=\#\Lambda _i$
,
![]() $N_i^j=\#\Lambda _i^j$
,
$N_i^j=\#\Lambda _i^j$
,
![]() $p_i^j=N_i^j/N_i$
. The numbers
$p_i^j=N_i^j/N_i$
. The numbers
![]() $(p_i^j)$
define a stochastic matrix, it has a probability vector
$(p_i^j)$
define a stochastic matrix, it has a probability vector
![]() $(p^i)$
verifying
$(p^i)$
verifying
![]() $\sum _{i \in A}p^i p_i^j=p^j, \sum _{i\in A}p^i=1.$
Set
$\sum _{i \in A}p^i p_i^j=p^j, \sum _{i\in A}p^i=1.$
Set
 $$ \begin{align*} p_{\unicode{x3bb}}^{\unicode{x3bb}'}=\begin{cases} 0 & \mbox{if } \omega(\unicode{x3bb}) \neq \alpha(\unicode{x3bb}'), \\ 1/N_{\omega(\unicode{x3bb})} & \mbox{if } \omega(\unicode{x3bb}) = \alpha(\unicode{x3bb}'), \end{cases} \end{align*} $$
$$ \begin{align*} p_{\unicode{x3bb}}^{\unicode{x3bb}'}=\begin{cases} 0 & \mbox{if } \omega(\unicode{x3bb}) \neq \alpha(\unicode{x3bb}'), \\ 1/N_{\omega(\unicode{x3bb})} & \mbox{if } \omega(\unicode{x3bb}) = \alpha(\unicode{x3bb}'), \end{cases} \end{align*} $$
and
![]() $p^{\unicode{x3bb} }=\frac {p^{\alpha (\unicode{x3bb} )}}{N_{\alpha (\unicode{x3bb} )}}.$
It is easily proved that
$p^{\unicode{x3bb} }=\frac {p^{\alpha (\unicode{x3bb} )}}{N_{\alpha (\unicode{x3bb} )}}.$
It is easily proved that
![]() $(p_{\unicode{x3bb} }^{\unicode{x3bb} '})$
is a stochastic matrix with probability vector
$(p_{\unicode{x3bb} }^{\unicode{x3bb} '})$
is a stochastic matrix with probability vector
![]() $(p^{\unicode{x3bb} })$
. Let
$(p^{\unicode{x3bb} })$
. Let
![]() $J^*=\mathbb {R}^{n-1}\times \mathbb {Z}^n$
denote the Pontryagin dual of J. Elements
$J^*=\mathbb {R}^{n-1}\times \mathbb {Z}^n$
denote the Pontryagin dual of J. Elements
![]() $\xi =(\mu _1,\ldots ,\mu _{n-1},m_1,\ldots ,m_n)\in J^*$
are homomorphisms from J to
$\xi =(\mu _1,\ldots ,\mu _{n-1},m_1,\ldots ,m_n)\in J^*$
are homomorphisms from J to
![]() $\mathbb {S}^1$
, given by
$\mathbb {S}^1$
, given by
Now suppose that for each
![]() $(\unicode{x3bb} ,\unicode{x3bb} ')\in \Lambda ^2$
, there is an element
$(\unicode{x3bb} ,\unicode{x3bb} ')\in \Lambda ^2$
, there is an element
![]() $a_{\unicode{x3bb} }^{\unicode{x3bb} '} \in J$
. Using this, we define for each
$a_{\unicode{x3bb} }^{\unicode{x3bb} '} \in J$
. Using this, we define for each
![]() $\xi \in J^*$
, a linear operator
$\xi \in J^*$
, a linear operator
![]() $T_{\xi }:\mathbb {C}^{\Lambda }\to \mathbb {C}^{\Lambda }$
given by
$T_{\xi }:\mathbb {C}^{\Lambda }\to \mathbb {C}^{\Lambda }$
given by
![]() $T_{\xi }((z_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda })=(w_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda }$
, where
$T_{\xi }((z_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda })=(w_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda }$
, where
![]() $w_\unicode{x3bb} =\sum _{\unicode{x3bb} '\in \Lambda } p_{\unicode{x3bb} }^{\unicode{x3bb} '}\xi (a_{\unicode{x3bb} }^{\unicode{x3bb} '})z_{\unicode{x3bb} '}.$
$w_\unicode{x3bb} =\sum _{\unicode{x3bb} '\in \Lambda } p_{\unicode{x3bb} }^{\unicode{x3bb} '}\xi (a_{\unicode{x3bb} }^{\unicode{x3bb} '})z_{\unicode{x3bb} '}.$
We endow the space
![]() $\mathbb {C}^{\Lambda }$
with the norm
$\mathbb {C}^{\Lambda }$
with the norm
![]() $\|(z_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda }\|^2=\sum _{\unicode{x3bb} \in \Lambda }p^{\unicode{x3bb} }|z_{\unicode{x3bb} }|^2.$
In a similar way to [Reference Moreira and Yoccoz7], a short computation shows that
$\|(z_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda }\|^2=\sum _{\unicode{x3bb} \in \Lambda }p^{\unicode{x3bb} }|z_{\unicode{x3bb} }|^2.$
In a similar way to [Reference Moreira and Yoccoz7], a short computation shows that
![]() $\| T_{\xi }\|\leq 1$
for all
$\| T_{\xi }\|\leq 1$
for all
![]() $\xi \in J^*$
.
$\xi \in J^*$
.
Assume that we have a family
![]() $\{E(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
of bounded measurable subsets of J, and consider the function
$\{E(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
of bounded measurable subsets of J, and consider the function
 $$ \begin{align*}n_{\unicode{x3bb}}(x)=\frac{1}{N_{\omega(\unicode{x3bb})}}\cdot \#\{\unicode{x3bb}'\in \Lambda_{\omega(\unicode{x3bb})}: B_{\rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset E(\unicode{x3bb}')\}.\end{align*} $$
$$ \begin{align*}n_{\unicode{x3bb}}(x)=\frac{1}{N_{\omega(\unicode{x3bb})}}\cdot \#\{\unicode{x3bb}'\in \Lambda_{\omega(\unicode{x3bb})}: B_{\rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset E(\unicode{x3bb}')\}.\end{align*} $$
Let
![]() $0<\tau <1$
, and denote by
$0<\tau <1$
, and denote by
![]() $E^*(\unicode{x3bb} )$
the set
$E^*(\unicode{x3bb} )$
the set
![]() $E^*(\unicode{x3bb} )=\{x\in J: n_{\unicode{x3bb} }(x)>\tau \}.$
$E^*(\unicode{x3bb} )=\{x\in J: n_{\unicode{x3bb} }(x)>\tau \}.$
Proposition 4.1. Suppose there exist
![]() $\Delta _0>0$
and
$\Delta _0>0$
and
![]() $k_{0}\in (0,1)$
such that
$k_{0}\in (0,1)$
such that
![]() $\| T_{\xi }\|<k_0$
for all
$\| T_{\xi }\|<k_0$
for all
![]() $\xi =(\mu _1,\ldots ,\mu _{n-1},m_1,\ldots ,m_n)$
, with
$\xi =(\mu _1,\ldots ,\mu _{n-1},m_1,\ldots ,m_n)$
, with
![]() $|\xi |=\max _j \{|\mu _j|,|m_j|\}\in [1,\Delta _0 \rho ^{-1}]$
. Then there exist
$|\xi |=\max _j \{|\mu _j|,|m_j|\}\in [1,\Delta _0 \rho ^{-1}]$
. Then there exist
![]() $k_1\in (0,1)$
,
$k_1\in (0,1)$
,
![]() $\epsilon>0$
, and
$\epsilon>0$
, and
![]() $\tau \in (0,1)$
depending only on
$\tau \in (0,1)$
depending only on
![]() $\Delta _0$
,
$\Delta _0$
,
![]() $k_0$
(and not on
$k_0$
(and not on
![]() $\rho $
) such that if
$\rho $
) such that if
![]() $\nu (E(\unicode{x3bb} ))\leq \epsilon $
for all
$\nu (E(\unicode{x3bb} ))\leq \epsilon $
for all
![]() $\unicode{x3bb} \in \Lambda $
, then
$\unicode{x3bb} \in \Lambda $
, then
Proof. Consider the functions
![]() $X_{\unicode{x3bb} }=1_{E(\unicode{x3bb} )},\ Y_{\unicode{x3bb} }(x)=\sum _{\unicode{x3bb} '\in \Lambda }p_{\unicode{x3bb} }^{\unicode{x3bb} '}X_{\unicode{x3bb} '}(x+a_{\unicode{x3bb} }^{\unicode{x3bb} '}),$
$X_{\unicode{x3bb} }=1_{E(\unicode{x3bb} )},\ Y_{\unicode{x3bb} }(x)=\sum _{\unicode{x3bb} '\in \Lambda }p_{\unicode{x3bb} }^{\unicode{x3bb} '}X_{\unicode{x3bb} '}(x+a_{\unicode{x3bb} }^{\unicode{x3bb} '}),$
 $$ \begin{align*} Z_{\unicode{x3bb}}(x)=\frac{1}{\nu(B_{\rho}(0))}\cdot \int_{B_{\rho}(0)}Y_{\unicode{x3bb}}(x-t)d\nu(t)=\frac{1}{\nu(B_{\rho}(0))} 1_{B_{\rho}(0)}\ast Y_{\unicode{x3bb}}(x). \end{align*} $$
$$ \begin{align*} Z_{\unicode{x3bb}}(x)=\frac{1}{\nu(B_{\rho}(0))}\cdot \int_{B_{\rho}(0)}Y_{\unicode{x3bb}}(x-t)d\nu(t)=\frac{1}{\nu(B_{\rho}(0))} 1_{B_{\rho}(0)}\ast Y_{\unicode{x3bb}}(x). \end{align*} $$
Note that
![]() $Z_{\unicode{x3bb} }(x)\geq n_{\unicode{x3bb} }(x)$
, then
$Z_{\unicode{x3bb} }(x)\geq n_{\unicode{x3bb} }(x)$
, then
![]() $\|Z_{\unicode{x3bb} }\|_{L^2}^2\geq \tau ^2 \nu (E^*(\unicode{x3bb} ))$
, which implies
$\|Z_{\unicode{x3bb} }\|_{L^2}^2\geq \tau ^2 \nu (E^*(\unicode{x3bb} ))$
, which implies
The Fourier transforms of
![]() $X_{\unicode{x3bb} }$
,
$X_{\unicode{x3bb} }$
,
![]() $Y_{\unicode{x3bb} }$
,
$Y_{\unicode{x3bb} }$
,
![]() $Z_{\unicode{x3bb} }$
are
$Z_{\unicode{x3bb} }$
are
 $$ \begin{align*} \hat{X}_{\unicode{x3bb}}(\xi)&=\int_{J}X_{\unicode{x3bb}}(x)\bar{\xi}(x)d\nu(x),\,\, \hat{Y}_{\unicode{x3bb}}(\xi)= \sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}\xi(a_{\unicode{x3bb}}^{\unicode{x3bb}'})\hat{X}_{\unicode{x3bb}'}(\xi),\\ \hat{Z}_{\unicode{x3bb}}(\xi)&=\frac{1}{\nu(B_{\rho}(0))} \hat{1}_{B_{\rho}(0)}\cdot \hat{Y}_{\unicode{x3bb}}(\xi)= \prod_{j=1}^{n-1}\frac{\sin(\mu_j\rho)}{\mu_j\rho} \prod_{j=1}^{n}\frac{\sin(m_j\rho)}{m_j\rho}\cdot \hat{Y}_{\unicode{x3bb}}(\xi), \end{align*} $$
$$ \begin{align*} \hat{X}_{\unicode{x3bb}}(\xi)&=\int_{J}X_{\unicode{x3bb}}(x)\bar{\xi}(x)d\nu(x),\,\, \hat{Y}_{\unicode{x3bb}}(\xi)= \sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}\xi(a_{\unicode{x3bb}}^{\unicode{x3bb}'})\hat{X}_{\unicode{x3bb}'}(\xi),\\ \hat{Z}_{\unicode{x3bb}}(\xi)&=\frac{1}{\nu(B_{\rho}(0))} \hat{1}_{B_{\rho}(0)}\cdot \hat{Y}_{\unicode{x3bb}}(\xi)= \prod_{j=1}^{n-1}\frac{\sin(\mu_j\rho)}{\mu_j\rho} \prod_{j=1}^{n}\frac{\sin(m_j\rho)}{m_j\rho}\cdot \hat{Y}_{\unicode{x3bb}}(\xi), \end{align*} $$
where
![]() $\xi =(\mu _1,\ldots ,\mu _{n-1},m_1,\ldots ,m_n)$
. Hence,
$\xi =(\mu _1,\ldots ,\mu _{n-1},m_1,\ldots ,m_n)$
. Hence,
![]() $|\hat {Z}_{\unicode{x3bb} }(\xi )|\leq |\hat {Y}_{\unicode{x3bb} }(\xi )|$
, and there exists
$|\hat {Z}_{\unicode{x3bb} }(\xi )|\leq |\hat {Y}_{\unicode{x3bb} }(\xi )|$
, and there exists
![]() $\tilde {k}_1\in (0,1)$
, depending only on
$\tilde {k}_1\in (0,1)$
, depending only on
![]() $\Delta _0$
, such that
$\Delta _0$
, such that
![]() $|\hat {Z}_{\unicode{x3bb} }(\xi )|\leq \tilde {k}_1|\hat {Y}_{\unicode{x3bb} }(\xi )|$
if
$|\hat {Z}_{\unicode{x3bb} }(\xi )|\leq \tilde {k}_1|\hat {Y}_{\unicode{x3bb} }(\xi )|$
if
![]() $|\xi |>\Delta _0 \rho ^{-1}$
. We estimate
$|\xi |>\Delta _0 \rho ^{-1}$
. We estimate
![]() $\sum _{\unicode{x3bb} \in \Lambda }p^{\unicode{x3bb} }|\hat {Z}_{\unicode{x3bb} }(\xi )|^2$
in various ways depending on
$\sum _{\unicode{x3bb} \in \Lambda }p^{\unicode{x3bb} }|\hat {Z}_{\unicode{x3bb} }(\xi )|^2$
in various ways depending on
![]() $|\xi |$
.
$|\xi |$
.
If
![]() $|\xi |<1$
, then
$|\xi |<1$
, then
 $$ \begin{align*} |\hat{Z}_{\unicode{x3bb}}(\xi)|\leq |\hat{Y}_{\unicode{x3bb}}(\xi)| \leq \int_{J}|Y_{\unicode{x3bb}}(x)|d\nu(x) \leq \sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}\nu(E(\unicode{x3bb}')), \end{align*} $$
$$ \begin{align*} |\hat{Z}_{\unicode{x3bb}}(\xi)|\leq |\hat{Y}_{\unicode{x3bb}}(\xi)| \leq \int_{J}|Y_{\unicode{x3bb}}(x)|d\nu(x) \leq \sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}\nu(E(\unicode{x3bb}')), \end{align*} $$
therefore,
 $$ \begin{align*} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}|\hat{Z}_{\unicode{x3bb}}(\xi)|^2 \leq \sum_{\unicode{x3bb}' \in \Lambda} \bigg( \sum_{\unicode{x3bb} \in \unicode{x3bb}}p^{\unicode{x3bb}}p_{\unicode{x3bb}}^{\unicode{x3bb}'}\bigg)\nu(E(\unicode{x3bb}'))^2 = \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}} \nu(E(\unicode{x3bb}))^2. \end{align*} $$
$$ \begin{align*} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}|\hat{Z}_{\unicode{x3bb}}(\xi)|^2 \leq \sum_{\unicode{x3bb}' \in \Lambda} \bigg( \sum_{\unicode{x3bb} \in \unicode{x3bb}}p^{\unicode{x3bb}}p_{\unicode{x3bb}}^{\unicode{x3bb}'}\bigg)\nu(E(\unicode{x3bb}'))^2 = \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}} \nu(E(\unicode{x3bb}))^2. \end{align*} $$
If
![]() $1\leq |\xi | \leq \Delta _{0}\rho ^{-1}$
,
$1\leq |\xi | \leq \Delta _{0}\rho ^{-1}$
,
note that we used the fact that
![]() $(\hat {Y}_{\unicode{x3bb} }(\xi ))_{\unicode{x3bb} \in \Lambda }=T_{\xi }((\hat {X}_{\unicode{x3bb} }(\xi ))_{\unicode{x3bb} \in \Lambda })$
.
$(\hat {Y}_{\unicode{x3bb} }(\xi ))_{\unicode{x3bb} \in \Lambda }=T_{\xi }((\hat {X}_{\unicode{x3bb} }(\xi ))_{\unicode{x3bb} \in \Lambda })$
.
If
![]() $|\xi |>\Delta _{0}\rho ^{-1}$
,
$|\xi |>\Delta _{0}\rho ^{-1}$
,
Combining all three inequalities, we get
 $$ \begin{align*} &\int_{J^*}\sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}|\hat{Z}_{\unicode{x3bb}}(\xi)|^2d\hat{\nu}(\xi) \\ &\quad\leq \int_{|\xi|<1} \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}} \nu(E(\unicode{x3bb}))^2 d\hat{\nu}(\xi)+ k_{0}^2\int_{1\leq |\xi|\leq \Delta_0\rho^{-1}} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}|\hat{X}_{\unicode{x3bb}}(\xi)|^2 d\hat{\nu}(\xi)\\ &\qquad+ \tilde{k}_1^2\int_{|\xi|>\Delta_0\rho^{-1}} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}|\hat{X}_{\unicode{x3bb}}(\xi)|^2 d\hat{\nu}(\xi). \end{align*} $$
$$ \begin{align*} &\int_{J^*}\sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}|\hat{Z}_{\unicode{x3bb}}(\xi)|^2d\hat{\nu}(\xi) \\ &\quad\leq \int_{|\xi|<1} \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}} \nu(E(\unicode{x3bb}))^2 d\hat{\nu}(\xi)+ k_{0}^2\int_{1\leq |\xi|\leq \Delta_0\rho^{-1}} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}|\hat{X}_{\unicode{x3bb}}(\xi)|^2 d\hat{\nu}(\xi)\\ &\qquad+ \tilde{k}_1^2\int_{|\xi|>\Delta_0\rho^{-1}} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}|\hat{X}_{\unicode{x3bb}}(\xi)|^2 d\hat{\nu}(\xi). \end{align*} $$
Hence,
Using Plancherel theorem and the fact that
![]() $\nu (E(\unicode{x3bb} ))=\|X_{\unicode{x3bb} }\|_{L^2}^2$
, we get
$\nu (E(\unicode{x3bb} ))=\|X_{\unicode{x3bb} }\|_{L^2}^2$
, we get
This together with equation (6) imply
Finally, we get the desired inequality setting
and taking
![]() $\epsilon $
small enough such that
$\epsilon $
small enough such that
![]() $\hat {\nu }(\{|\xi |<1\})\cdot \epsilon +\max \{k_0^2,\tilde {k}_1^2\}<1.$
$\hat {\nu }(\{|\xi |<1\})\cdot \epsilon +\max \{k_0^2,\tilde {k}_1^2\}<1.$
Let
![]() $\Delta _1>0$
be any positive number and consider
$\Delta _1>0$
be any positive number and consider
 $$ \begin{align*}\hat{n}_{\unicode{x3bb}}(x)=\frac{1}{\# \Lambda_{\omega(\unicode{x3bb})}}\cdot \#\{\unicode{x3bb}'\in \Lambda_{\omega(\unicode{x3bb})}:B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\cap E(\unicode{x3bb}')\neq \emptyset \};\end{align*} $$
$$ \begin{align*}\hat{n}_{\unicode{x3bb}}(x)=\frac{1}{\# \Lambda_{\omega(\unicode{x3bb})}}\cdot \#\{\unicode{x3bb}'\in \Lambda_{\omega(\unicode{x3bb})}:B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\cap E(\unicode{x3bb}')\neq \emptyset \};\end{align*} $$
define
![]() $\hat {E}(\unicode{x3bb} )=\{x\in J: \hat {n}_{\unicode{x3bb} }(x)>\tau \}$
. For a set
$\hat {E}(\unicode{x3bb} )=\{x\in J: \hat {n}_{\unicode{x3bb} }(x)>\tau \}$
. For a set
![]() $E\subset J$
, denote by
$E\subset J$
, denote by
![]() $V_{\delta }(E)$
the
$V_{\delta }(E)$
the
![]() $\delta $
-neighborhood of E.
$\delta $
-neighborhood of E.
Corollary 4.1. Under the same hypothesis as Proposition 4.1, let
![]() $k_4>0$
such that
$k_4>0$
such that
![]() $k_1<k_4<1$
; if we choose
$k_1<k_4<1$
; if we choose
![]() $\Delta>0$
big enough and
$\Delta>0$
big enough and
![]() $\epsilon _1>0$
small enough such that
$\epsilon _1>0$
small enough such that
 $$ \begin{align*} k_1\bigg(1+\frac{1+\Delta_1}{\Delta}\bigg)^{2n-1}<k_4,\,\,\, \epsilon_1 \bigg(1+\frac{1+\Delta_1}{\Delta}\bigg)^{2n-1} < \epsilon, \end{align*} $$
$$ \begin{align*} k_1\bigg(1+\frac{1+\Delta_1}{\Delta}\bigg)^{2n-1}<k_4,\,\,\, \epsilon_1 \bigg(1+\frac{1+\Delta_1}{\Delta}\bigg)^{2n-1} < \epsilon, \end{align*} $$
then
![]() $\nu (V_{\Delta \rho }(E(\unicode{x3bb} )))\leq \epsilon _1$
, for all
$\nu (V_{\Delta \rho }(E(\unicode{x3bb} )))\leq \epsilon _1$
, for all
![]() $\unicode{x3bb} \in \Lambda $
, implies that
$\unicode{x3bb} \in \Lambda $
, implies that
Proof. First observe that (see [Reference Lowther5])
 $$ \begin{align*}\nu(V_{\rho+\Delta\rho+\Delta_1\rho}(E(\unicode{x3bb})))\leq \bigg(1+\frac{1+\Delta_1}{\Delta}\bigg)^{2n-1} \nu(V_{\Delta\rho}(E(\unicode{x3bb}))).\end{align*} $$
$$ \begin{align*}\nu(V_{\rho+\Delta\rho+\Delta_1\rho}(E(\unicode{x3bb})))\leq \bigg(1+\frac{1+\Delta_1}{\Delta}\bigg)^{2n-1} \nu(V_{\Delta\rho}(E(\unicode{x3bb}))).\end{align*} $$
Now consider the family
![]() $A(\unicode{x3bb} )=V_{\rho +\Delta \rho +\Delta _1\rho }(E(\unicode{x3bb} ))$
; by our choice of
$A(\unicode{x3bb} )=V_{\rho +\Delta \rho +\Delta _1\rho }(E(\unicode{x3bb} ))$
; by our choice of
![]() $\epsilon _1$
, we can apply Proposition 4.1 to
$\epsilon _1$
, we can apply Proposition 4.1 to
![]() $A(\unicode{x3bb} )$
. Notice also that if
$A(\unicode{x3bb} )$
. Notice also that if
![]() $x\in V_{\Delta \rho }(\hat {E}(\unicode{x3bb} ))$
, then there exist
$x\in V_{\Delta \rho }(\hat {E}(\unicode{x3bb} ))$
, then there exist
![]() $y\in B_{\Delta \rho }(x)$
and
$y\in B_{\Delta \rho }(x)$
and
![]() $\tau \cdot \#\Lambda _{\omega (\unicode{x3bb} )}$
elements
$\tau \cdot \#\Lambda _{\omega (\unicode{x3bb} )}$
elements
![]() $\unicode{x3bb} '\in \Lambda _{\omega (\unicode{x3bb} )}$
such that
$\unicode{x3bb} '\in \Lambda _{\omega (\unicode{x3bb} )}$
such that
![]() $B_{\Delta _1 \rho }(y+a_{\unicode{x3bb} }^{\unicode{x3bb} '})\cap E(\unicode{x3bb} ')\neq \emptyset ,$
and thus
$B_{\Delta _1 \rho }(y+a_{\unicode{x3bb} }^{\unicode{x3bb} '})\cap E(\unicode{x3bb} ')\neq \emptyset ,$
and thus
![]() $B_{\rho }(x+a_{\unicode{x3bb} }^{\unicode{x3bb} '})\subset V_{\rho +\Delta \rho +\Delta _1\rho }(E(\unicode{x3bb} '))=A(\unicode{x3bb} ').$
$B_{\rho }(x+a_{\unicode{x3bb} }^{\unicode{x3bb} '})\subset V_{\rho +\Delta \rho +\Delta _1\rho }(E(\unicode{x3bb} '))=A(\unicode{x3bb} ').$
This shows that
![]() $V_{\Delta \rho }(\hat {E}(\unicode{x3bb} ))\subset A^*(\unicode{x3bb} )$
. Applying Proposition 4.1 to
$V_{\Delta \rho }(\hat {E}(\unicode{x3bb} ))\subset A^*(\unicode{x3bb} )$
. Applying Proposition 4.1 to
![]() $A(\unicode{x3bb} )$
gives
$A(\unicode{x3bb} )$
gives
 $$ \begin{align*}\sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(\hat{E}(\unicode{x3bb}))) &\leq \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(A^*(\unicode{x3bb})) \leq k_1 \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\rho+\Delta\rho+\Delta_1\rho}(E(\unicode{x3bb}))) \\ &\leq k_1\bigg(1+\frac{1+\Delta_1}{\Delta}\bigg)^{2n-1} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E(\unicode{x3bb})))\\ &\leq k_4 \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E(\unicode{x3bb}))).\\[-3.8pc] \end{align*} $$
$$ \begin{align*}\sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(\hat{E}(\unicode{x3bb}))) &\leq \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(A^*(\unicode{x3bb})) \leq k_1 \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\rho+\Delta\rho+\Delta_1\rho}(E(\unicode{x3bb}))) \\ &\leq k_1\bigg(1+\frac{1+\Delta_1}{\Delta}\bigg)^{2n-1} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E(\unicode{x3bb})))\\ &\leq k_4 \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E(\unicode{x3bb}))).\\[-3.8pc] \end{align*} $$
4.2 Proof of Theorem A
In this subsection, we will prove the multidimensional conformal scale recurrence lemma. First we will fix the values of the main parameters playing a role in the proof. This is done to make it clear that there are no contradictions between their values.
Start by choosing a positive constant
![]() $\mu $
such that
$\mu $
such that
![]() $-\log r^{\underline {\theta }}_{\underline {c}}<\mu $
for any
$-\log r^{\underline {\theta }}_{\underline {c}}<\mu $
for any
![]() $\underline {\theta }\in \Sigma _j^{-}$
, and
$\underline {\theta }\in \Sigma _j^{-}$
, and
![]() $\underline {c}=(c_0,c_1)\in \Sigma _j^\textit{fin}$
a finite sequence with only two symbols. The choice of
$\underline {c}=(c_0,c_1)\in \Sigma _j^\textit{fin}$
a finite sequence with only two symbols. The choice of
![]() $\mu $
and the equation
$\mu $
and the equation
![]() $r^{\underline {\theta }}_{\underline {b}\underline {c}}=r^{\underline {\theta }}_{\underline {b}}\cdot r^{\underline {\theta }\underline {b}}_{\underline {c}}$
imply that
$r^{\underline {\theta }}_{\underline {b}\underline {c}}=r^{\underline {\theta }}_{\underline {b}}\cdot r^{\underline {\theta }\underline {b}}_{\underline {c}}$
imply that
![]() $\log r^{\underline {\theta }}_{\underline {b}\underline {c}}>\log r^{\underline {\theta }}_{\underline {b}}-\mu .$
This is saying that as the length of
$\log r^{\underline {\theta }}_{\underline {b}\underline {c}}>\log r^{\underline {\theta }}_{\underline {b}}-\mu .$
This is saying that as the length of
![]() $\underline {b}$
increases, the number
$\underline {b}$
increases, the number
![]() $\log r^{\underline {\theta }}_{\underline {b}}$
decreases by steps no bigger than
$\log r^{\underline {\theta }}_{\underline {b}}$
decreases by steps no bigger than
![]() $\mu $
.
$\mu $
.
Now choose
![]() $c>0$
such that
$c>0$
such that
![]() $c^{-1}\mathrm {diam}(G(\underline {a}^j))\leq \mathrm {diam}(G^{\underline {\theta }^j}(\underline {a}^j)) \leq c\, \mathrm {diam}(G(\underline {a}^j))$
for
$c^{-1}\mathrm {diam}(G(\underline {a}^j))\leq \mathrm {diam}(G^{\underline {\theta }^j}(\underline {a}^j)) \leq c\, \mathrm {diam}(G(\underline {a}^j))$
for
![]() $\underline {a}^j\in \Sigma _j^\textit{fin}$
,
$\underline {a}^j\in \Sigma _j^\textit{fin}$
,
![]() $\underline {\theta }^j \in \Sigma _j^-$
. These constants only depend on
$\underline {\theta }^j \in \Sigma _j^-$
. These constants only depend on
![]() $K_1,\ldots ,K_n$
. Fix
$K_1,\ldots ,K_n$
. Fix
![]() $\tilde {c}_0>0$
such that
$\tilde {c}_0>0$
such that
We will use Proposition 4.1 with the following data:
 $$ \begin{align*} \Lambda&=\Sigma_1 (\tilde{c}_0,\rho)\times\cdots\times \Sigma_n (\tilde{c}_0,\rho),\\ A&=\mathbb{A}_1\times \cdots\times \mathbb{A}_n,\\ \alpha(\underline{a}^1,\ldots,\underline{a}^n)&=(a^1_0,\ldots,a^n_0),\\ \omega(\underline{a}^1,\ldots,\underline{a}^n)&=(a^1_{m_1},\ldots,a^n_{m_n}),\\ a_{\unicode{x3bb}}^{\unicode{x3bb}'}&=\bigg(\log \frac{r_{\underline{b}^1}^{\underline{\theta}^1}}{r_{\underline{b}^n}^{\underline{\theta}^n}},\ldots,\log \frac{r_{\underline{b}^{n-1}}^{\underline{\theta}^{n-1}}}{r_{\underline{b}^n}^{\underline{\theta}^n}},v_{\underline{b}^1}^{\underline{\theta}^1},\ldots,v_{\underline{b}^n}^{\underline{\theta}^n}\bigg), \end{align*} $$
$$ \begin{align*} \Lambda&=\Sigma_1 (\tilde{c}_0,\rho)\times\cdots\times \Sigma_n (\tilde{c}_0,\rho),\\ A&=\mathbb{A}_1\times \cdots\times \mathbb{A}_n,\\ \alpha(\underline{a}^1,\ldots,\underline{a}^n)&=(a^1_0,\ldots,a^n_0),\\ \omega(\underline{a}^1,\ldots,\underline{a}^n)&=(a^1_{m_1},\ldots,a^n_{m_n}),\\ a_{\unicode{x3bb}}^{\unicode{x3bb}'}&=\bigg(\log \frac{r_{\underline{b}^1}^{\underline{\theta}^1}}{r_{\underline{b}^n}^{\underline{\theta}^n}},\ldots,\log \frac{r_{\underline{b}^{n-1}}^{\underline{\theta}^{n-1}}}{r_{\underline{b}^n}^{\underline{\theta}^n}},v_{\underline{b}^1}^{\underline{\theta}^1},\ldots,v_{\underline{b}^n}^{\underline{\theta}^n}\bigg), \end{align*} $$
where
![]() $\underline {a}^j=(a^j_0,\ldots ,a^j_{m_j})$
,
$\underline {a}^j=(a^j_0,\ldots ,a^j_{m_j})$
,
![]() $\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)$
,
$\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)$
,
![]() $\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^n)$
, and
$\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^n)$
, and
![]() $\underline {\theta }^j \in \Sigma _j^-$
finishes in
$\underline {\theta }^j \in \Sigma _j^-$
finishes in
![]() $\underline {a}^j$
,
$\underline {a}^j$
,
![]() $1\leq j\leq n$
. (For every
$1\leq j\leq n$
. (For every
![]() $\underline {a}^j\in \Sigma _j^\textit{fin}$
, we choose, arbitrarily, an element
$\underline {a}^j\in \Sigma _j^\textit{fin}$
, we choose, arbitrarily, an element
![]() $\underline {\theta }^j\in \Sigma _j^-$
that ends in
$\underline {\theta }^j\in \Sigma _j^-$
that ends in
![]() $\underline {a}^j$
. Using this, we define
$\underline {a}^j$
. Using this, we define
![]() $a_{\unicode{x3bb} }^{\unicode{x3bb} '}$
.) Assume that the hypothesis of Proposition 4.1 holds, namely that there exist
$a_{\unicode{x3bb} }^{\unicode{x3bb} '}$
.) Assume that the hypothesis of Proposition 4.1 holds, namely that there exist
![]() $\Delta _0$
,
$\Delta _0$
,
![]() $k_0$
such that
$k_0$
such that
![]() $\| T_{\xi }\|\leq k_0$
for all
$\| T_{\xi }\|\leq k_0$
for all
![]() $|\xi |\in [1,\Delta _0\rho ^{-1}]$
; this will be verified in the next subsection. Applying the proposition in this setting gives constants
$|\xi |\in [1,\Delta _0\rho ^{-1}]$
; this will be verified in the next subsection. Applying the proposition in this setting gives constants
![]() $k_1$
,
$k_1$
,
![]() $\tau $
,
$\tau $
,
![]() $\epsilon $
.
$\epsilon $
.
Now fix
![]() $k_4,k_5>0$
such that
$k_4,k_5>0$
such that
![]() $k_1<k_4<k_5<1$
and
$k_1<k_4<k_5<1$
and
![]() $\delta>0$
such that
$\delta>0$
such that
where
![]() $C_2>0$
,
$C_2>0$
,
![]() $L>0$
are constants such that
$L>0$
are constants such that
for any
![]() $i\in A$
,
$i\in A$
,
![]() $\unicode{x3bb} \in \Lambda $
, and
$\unicode{x3bb} \in \Lambda $
, and
![]() $C_4>0$
is defined by equation (19). All these constants depend only on
$C_4>0$
is defined by equation (19). All these constants depend only on
![]() $\tilde {c}_0$
.
$\tilde {c}_0$
.
Fix
![]() $r>0$
such that
$r>0$
such that
 $$ \begin{align} 2r>\delta^{-1}\bigg(9+\frac{1}{4}\bigg)\log (c\tilde{c}_0). \end{align} $$
$$ \begin{align} 2r>\delta^{-1}\bigg(9+\frac{1}{4}\bigg)\log (c\tilde{c}_0). \end{align} $$
The choice of
![]() $\mu $
and
$\mu $
and
![]() $\tilde {c}_0$
allow us to find
$\tilde {c}_0$
allow us to find
![]() $\rho _{1}>0$
, small enough, such that for any family of intervals
$\rho _{1}>0$
, small enough, such that for any family of intervals
![]() $I_1,\ldots , I_{n-1}$
, with
$I_1,\ldots , I_{n-1}$
, with
![]() $\mathrm {diam}(I_j)\geq 2 \log (c \tilde {c}_0)$
, any
$\mathrm {diam}(I_j)\geq 2 \log (c \tilde {c}_0)$
, any
![]() $x=(t,v)\in J$
with
$x=(t,v)\in J$
with
![]() $\mathrm {dist}(t_j,I_j)\leq \delta ^{-1}(9+\tfrac 14)\log (c\tilde {c}_0)$
, and any
$\mathrm {dist}(t_j,I_j)\leq \delta ^{-1}(9+\tfrac 14)\log (c\tilde {c}_0)$
, and any
![]() $\unicode{x3bb} \in \Lambda $
, there exists
$\unicode{x3bb} \in \Lambda $
, there exists
![]() $\unicode{x3bb} _0=(\underline {b}^1,\ldots ,\underline {b}^n) \in \Sigma _1^\textit{fin}\hspace{-0.5pt}\times\hspace{-0.5pt} \cdots \hspace{-0.5pt}\times\hspace{-0.5pt} \Sigma _n^\textit{fin}$
with the property
$\unicode{x3bb} _0=(\underline {b}^1,\ldots ,\underline {b}^n) \in \Sigma _1^\textit{fin}\hspace{-0.5pt}\times\hspace{-0.5pt} \cdots \hspace{-0.5pt}\times\hspace{-0.5pt} \Sigma _n^\textit{fin}$
with the property
![]() $x+a_{\unicode{x3bb} }^{\unicode{x3bb} _0}\in I_1\times \cdots \times I_{n-1}\times \mathbb {T}^{n},$
and
$x+a_{\unicode{x3bb} }^{\unicode{x3bb} _0}\in I_1\times \cdots \times I_{n-1}\times \mathbb {T}^{n},$
and
![]() $\mathrm {diam} (G({\underline {b}^j}))>\rho _1$
,
$\mathrm {diam} (G({\underline {b}^j}))>\rho _1$
,
![]() $1\leq j\leq n$
. Choose
$1\leq j\leq n$
. Choose
![]() $c_0>\tilde {c}_0$
big enough such that
$c_0>\tilde {c}_0$
big enough such that
for all
![]() $\unicode{x3bb} _0=(\underline {b}^1,\ldots ,\underline {b}^n)$
, such that
$\unicode{x3bb} _0=(\underline {b}^1,\ldots ,\underline {b}^n)$
, such that
![]() $\mathrm {diam} (G({\underline {b}^j}))>\rho _1$
,
$\mathrm {diam} (G({\underline {b}^j}))>\rho _1$
,
![]() $1\leq j\leq n$
, and any
$1\leq j\leq n$
, and any
![]() $\unicode{x3bb} \in \Lambda $
with
$\unicode{x3bb} \in \Lambda $
with
![]() $\omega (\unicode{x3bb} _0)=\alpha (\unicode{x3bb} )$
. (If
$\omega (\unicode{x3bb} _0)=\alpha (\unicode{x3bb} )$
. (If
![]() $\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)$
,
$\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)$
,
![]() $\unicode{x3bb} _0=(\underline {b}^1,\ldots ,\underline {b}^n)$
, with
$\unicode{x3bb} _0=(\underline {b}^1,\ldots ,\underline {b}^n)$
, with
![]() $\omega (\unicode{x3bb} _0)=\alpha (\unicode{x3bb} )$
, then
$\omega (\unicode{x3bb} _0)=\alpha (\unicode{x3bb} )$
, then
![]() $\unicode{x3bb} _0\unicode{x3bb} =(\underline {b}^1\underline {a}^1,\ldots ,\underline {b}^n\underline {a}^n)$
.)
$\unicode{x3bb} _0\unicode{x3bb} =(\underline {b}^1\underline {a}^1,\ldots ,\underline {b}^n\underline {a}^n)$
.)
We also fix a constant
![]() $\Delta _1>0$
that should be big enough to verify equation (15); this is a condition that only depends on
$\Delta _1>0$
that should be big enough to verify equation (15); this is a condition that only depends on
![]() $c_0$
. Finally, we choose
$c_0$
. Finally, we choose
![]() $\Delta $
,
$\Delta $
,
![]() $\epsilon _1$
as in Corollary 4.1.
$\epsilon _1$
as in Corollary 4.1.
Notice that
![]() $\Lambda '=\Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
contains
$\Lambda '=\Sigma _1(c_0,\rho )\times \cdots \times \Sigma _n(c_0,\rho )$
contains
![]() $\Lambda $
. Choose a function
$\Lambda $
. Choose a function
![]() $\varphi :\Lambda '\to \Lambda $
such that we have the following properties.
$\varphi :\Lambda '\to \Lambda $
such that we have the following properties.
-
(a) If
 $\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)\in \Lambda '$
and
$\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)\in \Lambda '$
and
 $\varphi (\unicode{x3bb} )=(\underline {b}^1,\ldots ,\underline {b}^n)$
, then either
$\varphi (\unicode{x3bb} )=(\underline {b}^1,\ldots ,\underline {b}^n)$
, then either
 $\underline {a}^j$
ends with
$\underline {a}^j$
ends with
 $\underline {b}^j$
or
$\underline {b}^j$
or
 $\underline {b}^j$
ends with
$\underline {b}^j$
ends with
 $\underline {a}^j$
for every
$\underline {a}^j$
for every
 $1\leq j\leq n$
.
$1\leq j\leq n$
. -
(b)
 $\varphi (\unicode{x3bb} )=\unicode{x3bb} \ \text { for all } \unicode{x3bb} \in \Lambda $
.
$\varphi (\unicode{x3bb} )=\unicode{x3bb} \ \text { for all } \unicode{x3bb} \in \Lambda $
.
Thanks to properties (a),(b) of
![]() $\varphi $
, there are constants
$\varphi $
, there are constants
![]() $T_1$
,
$T_1$
,
![]() $T_2$
depending only on
$T_2$
depending only on
![]() $c_0,\, \tilde {c}_0$
, and not on
$c_0,\, \tilde {c}_0$
, and not on
![]() $\rho $
, such that
$\rho $
, such that
![]() $1\leq T_1\leq \#\varphi ^{-1}(\unicode{x3bb} )\leq T_2 \text { for all } \unicode{x3bb} \in \Lambda .$
$1\leq T_1\leq \#\varphi ^{-1}(\unicode{x3bb} )\leq T_2 \text { for all } \unicode{x3bb} \in \Lambda .$
We show that we can suppose
![]() $F(\unicode{x3bb} )=F(\varphi (\unicode{x3bb} ))$
. Assume that for the given values of
$F(\unicode{x3bb} )=F(\varphi (\unicode{x3bb} ))$
. Assume that for the given values of
![]() $c_0$
and r, there exist
$c_0$
and r, there exist
![]() $c_1,c_2,c_3,\rho _0>0$
such that the scale recurrence lemma is verified in the special case when
$c_1,c_2,c_3,\rho _0>0$
such that the scale recurrence lemma is verified in the special case when
![]() $F(\unicode{x3bb} )=F(\varphi (\unicode{x3bb} )) \text { for all } \unicode{x3bb} \in \Lambda '.$
We find new values for
$F(\unicode{x3bb} )=F(\varphi (\unicode{x3bb} )) \text { for all } \unicode{x3bb} \in \Lambda '.$
We find new values for
![]() $c_1,c_2,c_3, \rho _0>0$
verifying the lemma in the general case. In fact, we do not need to change
$c_1,c_2,c_3, \rho _0>0$
verifying the lemma in the general case. In fact, we do not need to change
![]() $c_2,c_3,\rho _0>0$
, just redefine
$c_2,c_3,\rho _0>0$
, just redefine
![]() $c_1$
as
$c_1$
as
![]() $c_1/T_2$
. Given a family
$c_1/T_2$
. Given a family
![]() $\{F(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda '}$
with
$\{F(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda '}$
with
![]() $\nu (J_r\setminus F(\unicode{x3bb} ))\leq c_1/T_2$
, consider
$\nu (J_r\setminus F(\unicode{x3bb} ))\leq c_1/T_2$
, consider
![]() $\tilde {F}(\unicode{x3bb} )=\bigcap _{\unicode{x3bb} '\in \,\varphi ^{-1}(\varphi (\unicode{x3bb} ))}F(\unicode{x3bb} ').$
This new family verifies
$\tilde {F}(\unicode{x3bb} )=\bigcap _{\unicode{x3bb} '\in \,\varphi ^{-1}(\varphi (\unicode{x3bb} ))}F(\unicode{x3bb} ').$
This new family verifies
![]() $\tilde {F}(\unicode{x3bb} )=\tilde {F}(\varphi (\unicode{x3bb} ))$
, moreover,
$\tilde {F}(\unicode{x3bb} )=\tilde {F}(\varphi (\unicode{x3bb} ))$
, moreover,
![]() $\nu (J_r\setminus \tilde {F}(\unicode{x3bb} ))\leq c_1$
, then there exists
$\nu (J_r\setminus \tilde {F}(\unicode{x3bb} ))\leq c_1$
, then there exists
![]() $\tilde {F}^*(\unicode{x3bb} )$
with the properties of the scale recurrence lemma. Taking
$\tilde {F}^*(\unicode{x3bb} )$
with the properties of the scale recurrence lemma. Taking
![]() $F^*(\unicode{x3bb} )=\tilde {F}^*(\unicode{x3bb} )$
gives the lemma in the general case.
$F^*(\unicode{x3bb} )=\tilde {F}^*(\unicode{x3bb} )$
gives the lemma in the general case.
For the scale recurrence lemma to hold, it is enough to prove the following statement.
Statement 4.1. For the given values of
![]() $c_0$
and r, there exist
$c_0$
and r, there exist
![]() $c_1,c_2,c_3,\rho _0>0$
with the following properties: given
$c_1,c_2,c_3,\rho _0>0$
with the following properties: given
![]() $0<\rho <\rho _0$
and a family
$0<\rho <\rho _0$
and a family
![]() $F(\unicode{x3bb} )$
of subsets of
$F(\unicode{x3bb} )$
of subsets of
![]() $J_r$
,
$J_r$
,
![]() $\unicode{x3bb} \in \Lambda =\Sigma _1(\tilde {c}_0,\rho )\times \cdots \times \Sigma _n(\tilde {c}_0,\rho )$
such that
$\unicode{x3bb} \in \Lambda =\Sigma _1(\tilde {c}_0,\rho )\times \cdots \times \Sigma _n(\tilde {c}_0,\rho )$
such that
![]() $\nu (J_r\setminus F(\unicode{x3bb} ))\leq c_1 \text { for all } \unicode{x3bb} ,$
there is another family
$\nu (J_r\setminus F(\unicode{x3bb} ))\leq c_1 \text { for all } \unicode{x3bb} ,$
there is another family
![]() $F^*(\unicode{x3bb} )$
of subsets of
$F^*(\unicode{x3bb} )$
of subsets of
![]() $J_r$
satisfying the following properties.
$J_r$
satisfying the following properties.
-
(i) For any
 $\unicode{x3bb} \in \Lambda $
,
$\unicode{x3bb} \in \Lambda $
,
 $F^*(\unicode{x3bb} )$
is contained in the
$F^*(\unicode{x3bb} )$
is contained in the
 $c_2 \rho $
-neighborhood of
$c_2 \rho $
-neighborhood of
 $F(\unicode{x3bb} )$
.
$F(\unicode{x3bb} )$
. -
(ii) Let
 $\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)\in \Lambda $
,
$\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)\in \Lambda $
,
 $(t,v)\in F^*(\unicode{x3bb} )$
; there exist at least
$(t,v)\in F^*(\unicode{x3bb} )$
; there exist at least
 $c_3\rho ^{-(d_1+\cdots +d_n)}$
elements
$c_3\rho ^{-(d_1+\cdots +d_n)}$
elements
 $\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^n)\in \Lambda '$
(with
$\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^n)\in \Lambda '$
(with
 $\underline {b}^j$
starting with the last letter of
$\underline {b}^j$
starting with the last letter of
 $\underline {a}^j$
) such that if
$\underline {a}^j$
) such that if
 $\underline {\theta }^j \in \Sigma _j^{-}$
,
$\underline {\theta }^j \in \Sigma _j^{-}$
,
 $1\leq j\leq n$
, verify
$1\leq j\leq n$
, verify
 $\underline {\theta }^j \wedge \underline {a}^j\in \Sigma _j(c_0,\rho )$
,
$\underline {\theta }^j \wedge \underline {a}^j\in \Sigma _j(c_0,\rho )$
,
 $1\leq j\leq n$
and the
$1\leq j\leq n$
and the $$ \begin{align*}T_{\underline{b}^1,\ldots,\underline{b}^n}(\underline{\theta}^1,\ldots,\underline{\theta}^n,t,v)=(\underline{\theta}^1\underline{b}^1,\ldots,\underline{\theta}^n\underline{b}^n,\tilde{t},\tilde{v})\end{align*} $$
$$ \begin{align*}T_{\underline{b}^1,\ldots,\underline{b}^n}(\underline{\theta}^1,\ldots,\underline{\theta}^n,t,v)=(\underline{\theta}^1\underline{b}^1,\ldots,\underline{\theta}^n\underline{b}^n,\tilde{t},\tilde{v})\end{align*} $$
 $\rho $
-neighborhood of
$\rho $
-neighborhood of
 $(\tilde {t},\tilde {v})\in J$
is contained in
$(\tilde {t},\tilde {v})\in J$
is contained in
 $F^*(\varphi (\unicode{x3bb} '))$
.
$F^*(\varphi (\unicode{x3bb} '))$
.
-
(iii)
 $\nu (F^*(\unicode{x3bb} ))\geq \nu (J_r)/2$
for at least
$\nu (F^*(\unicode{x3bb} ))\geq \nu (J_r)/2$
for at least
 $T_2/(T_2+T_1)$
of the
$T_2/(T_2+T_1)$
of the
 $\unicode{x3bb} \in \Lambda $
.
$\unicode{x3bb} \in \Lambda $
.
The difference between Statement 4.1 and the scale recurrence lemma is that
![]() $\Lambda $
is parameterizing the sets
$\Lambda $
is parameterizing the sets
![]() $F(\unicode{x3bb} )$
instead of
$F(\unicode{x3bb} )$
instead of
![]() $\Lambda '$
; however,
$\Lambda '$
; however,
![]() $\Lambda '$
, which is much bigger than
$\Lambda '$
, which is much bigger than
![]() $\Lambda $
, still parameterizes the set of renormalization operators.
$\Lambda $
, still parameterizes the set of renormalization operators.
Let
![]() $\{F(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda '}$
be a family of sets as in the scale recurrence lemma. We can suppose that
$\{F(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda '}$
be a family of sets as in the scale recurrence lemma. We can suppose that
![]() $F(\unicode{x3bb} )=F(\varphi (\unicode{x3bb} ))$
. Now assume that Statement 4.1 holds, then we can apply it to the restricted family
$F(\unicode{x3bb} )=F(\varphi (\unicode{x3bb} ))$
. Now assume that Statement 4.1 holds, then we can apply it to the restricted family
![]() $\{F(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
, which produces another family
$\{F(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
, which produces another family
![]() $\{F^*(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
. We extend it to
$\{F^*(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
. We extend it to
![]() $\unicode{x3bb} \in \Lambda '$
by
$\unicode{x3bb} \in \Lambda '$
by
![]() $F^*(\unicode{x3bb} )=F^*(\varphi (\unicode{x3bb} ))$
. It is easily seen that
$F^*(\unicode{x3bb} )=F^*(\varphi (\unicode{x3bb} ))$
. It is easily seen that
![]() $\{F^*(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda '}$
verifies the desired properties on the scale recurrence lemma. From now on, we will focus in the proof of Statement 4.1.
$\{F^*(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda '}$
verifies the desired properties on the scale recurrence lemma. From now on, we will focus in the proof of Statement 4.1.
Suppose we have a family of sets
![]() $\{F(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
. Define
$\{F(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
. Define
![]() $E_0(\unicode{x3bb} )=J_r\setminus V_{\Delta \rho }(F(\unicode{x3bb} ))$
,
$E_0(\unicode{x3bb} )=J_r\setminus V_{\Delta \rho }(F(\unicode{x3bb} ))$
,
![]() $\unicode{x3bb} \in \Lambda .$
Now we define recursively two families of sets
$\unicode{x3bb} \in \Lambda .$
Now we define recursively two families of sets
![]() $\{E_m(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
and
$\{E_m(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
and
![]() $\{\tilde {E}_m(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
. The set
$\{\tilde {E}_m(\unicode{x3bb} )\}_{\unicode{x3bb} \in \Lambda }$
. The set
![]() $\tilde {E}_m(\unicode{x3bb} )$
is given by the
$\tilde {E}_m(\unicode{x3bb} )$
is given by the
![]() $x\in J_r$
such that (when
$x\in J_r$
such that (when
![]() $\unicode{x3bb} '\in \Lambda '\setminus \Lambda $
, the element
$\unicode{x3bb} '\in \Lambda '\setminus \Lambda $
, the element
![]() $a_{\unicode{x3bb} }^{\unicode{x3bb} '}$
is defined in the same way as when
$a_{\unicode{x3bb} }^{\unicode{x3bb} '}$
is defined in the same way as when
![]() $\unicode{x3bb} ,\unicode{x3bb} ' \in \Lambda $
)
$\unicode{x3bb} ,\unicode{x3bb} ' \in \Lambda $
)
and
![]() $E_{m+1}(\unicode{x3bb} )=E_0(\unicode{x3bb} )\cup \tilde {E}_m(\unicode{x3bb} )$
. (In fact, since
$E_{m+1}(\unicode{x3bb} )=E_0(\unicode{x3bb} )\cup \tilde {E}_m(\unicode{x3bb} )$
. (In fact, since
![]() $\tilde {E}_j(\unicode{x3bb} ) \subset \tilde {E}_{j+1}(\unicode{x3bb} )$
, we have
$\tilde {E}_j(\unicode{x3bb} ) \subset \tilde {E}_{j+1}(\unicode{x3bb} )$
, we have
![]() $E_m(\unicode{x3bb} )=E_0(\unicode{x3bb} )\cup \tilde {E}_0(\unicode{x3bb} )\cup \cdots \cup \tilde {E}_{m-1}(\unicode{x3bb} )$
.) The value of
$E_m(\unicode{x3bb} )=E_0(\unicode{x3bb} )\cup \tilde {E}_0(\unicode{x3bb} )\cup \cdots \cup \tilde {E}_{m-1}(\unicode{x3bb} )$
.) The value of
![]() $c_3$
will be fixed during the proof of the next lemma. Note that for
$c_3$
will be fixed during the proof of the next lemma. Note that for
![]() $x\in \tilde {E}_0(\unicode{x3bb} )$
, one has
$x\in \tilde {E}_0(\unicode{x3bb} )$
, one has
 $$ \begin{align*}\{\unicode{x3bb}'\in \Lambda':\,B_{\Delta_1\rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})&\subset J_r\setminus E_1(\varphi(\unicode{x3bb}'))\}\\ &\subset \{\unicode{x3bb}'\in \Lambda':\,B_{\Delta_1\rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset J_r \setminus E_0(\varphi(\unicode{x3bb}'))\},\end{align*} $$
$$ \begin{align*}\{\unicode{x3bb}'\in \Lambda':\,B_{\Delta_1\rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})&\subset J_r\setminus E_1(\varphi(\unicode{x3bb}'))\}\\ &\subset \{\unicode{x3bb}'\in \Lambda':\,B_{\Delta_1\rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset J_r \setminus E_0(\varphi(\unicode{x3bb}'))\},\end{align*} $$
and hence
![]() $\tilde {E}_0(\unicode{x3bb} )\subset \tilde {E}_1(\unicode{x3bb} )$
. Analogously, one proves that
$\tilde {E}_0(\unicode{x3bb} )\subset \tilde {E}_1(\unicode{x3bb} )$
. Analogously, one proves that
![]() $\tilde {E}_m(\unicode{x3bb} )\subset \tilde {E}_{m+1}(\unicode{x3bb} )$
,
$\tilde {E}_m(\unicode{x3bb} )\subset \tilde {E}_{m+1}(\unicode{x3bb} )$
,
![]() $E_m(\unicode{x3bb} )\subset E_{m+1}(\unicode{x3bb} )$
for all m.
$E_m(\unicode{x3bb} )\subset E_{m+1}(\unicode{x3bb} )$
for all m.
Lemma 4.1. If
![]() $c_1$
,
$c_1$
,
![]() $c_3$
,
$c_3$
,
![]() $\rho _0$
are sufficiently small, then
$\rho _0$
are sufficiently small, then
 $$ \begin{align} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb}))) &\leq \frac{\nu(J_{r+\Delta \rho}\setminus J_r)+c_1}{1-k_5}. \end{align} $$
$$ \begin{align} \sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb}))) &\leq \frac{\nu(J_{r+\Delta \rho}\setminus J_r)+c_1}{1-k_5}. \end{align} $$
Before proving the lemma, we will use it to prove Statement 4.1. Consider
![]() $E_{\infty }(\unicode{x3bb} )=\bigcup _{m\geq 0}E_m(\unicode{x3bb} )$
; thanks to equation (13), we have
$E_{\infty }(\unicode{x3bb} )=\bigcup _{m\geq 0}E_m(\unicode{x3bb} )$
; thanks to equation (13), we have
 $$ \begin{align}\sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_{\infty}(\unicode{x3bb}))) \leq \frac{\nu(J_{r+\Delta \rho}\setminus J_r)+c_1}{1-k_5}.\end{align} $$
$$ \begin{align}\sum_{\unicode{x3bb} \in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_{\infty}(\unicode{x3bb}))) \leq \frac{\nu(J_{r+\Delta \rho}\setminus J_r)+c_1}{1-k_5}.\end{align} $$
Now define
![]() $F^*(\unicode{x3bb} )=J_r\setminus E_{\infty }(\unicode{x3bb} )$
. We will prove that this family of sets has the desired properties.
$F^*(\unicode{x3bb} )=J_r\setminus E_{\infty }(\unicode{x3bb} )$
. We will prove that this family of sets has the desired properties.
(i) Since
![]() $E_0(\unicode{x3bb} )\subset E_{\infty }(\unicode{x3bb} )$
then
$E_0(\unicode{x3bb} )\subset E_{\infty }(\unicode{x3bb} )$
then
![]() $F^*(\unicode{x3bb} )\subset J_r\setminus E_0(\unicode{x3bb} )=V_{\Delta \rho }(F(\unicode{x3bb} ))$
, choosing
$F^*(\unicode{x3bb} )\subset J_r\setminus E_0(\unicode{x3bb} )=V_{\Delta \rho }(F(\unicode{x3bb} ))$
, choosing
![]() $c_2=\Delta $
gives the first property.
$c_2=\Delta $
gives the first property.
(ii) Let
![]() $x\in F^*(\unicode{x3bb} )$
, then
$x\in F^*(\unicode{x3bb} )$
, then
![]() $x\notin \tilde {E}_m(\unicode{x3bb} )$
and the set
$x\notin \tilde {E}_m(\unicode{x3bb} )$
and the set
has more than
![]() $c_3\rho ^{-(d_1+\cdots +d_n)}$
elements for all m. Moreover, since
$c_3\rho ^{-(d_1+\cdots +d_n)}$
elements for all m. Moreover, since
![]() $E_m(\varphi (\unicode{x3bb} '))\subset E_{m+1}(\varphi (\unicode{x3bb} '))$
, one has
$E_m(\varphi (\unicode{x3bb} '))\subset E_{m+1}(\varphi (\unicode{x3bb} '))$
, one has
![]() $A_{m+1}\subset A_m$
and then
$A_{m+1}\subset A_m$
and then
![]() $\#(\bigcap _{m\geq 0}A_m)\geq c_3\rho ^{-(d_1+\cdots +d_n)}.$
Therefore,
$\#(\bigcap _{m\geq 0}A_m)\geq c_3\rho ^{-(d_1+\cdots +d_n)}.$
Therefore,
To finish, it is enough to prove that for any
![]() $\tilde {\underline {\theta }}^1,\ldots,\tilde {\underline {\theta }}^n $
such that
$\tilde {\underline {\theta }}^1,\ldots,\tilde {\underline {\theta }}^n $
such that
![]() $\tilde {\underline {\theta }}^j\wedge \underline {a}^j\in \Sigma _j(c_0,\rho )$
,
$\tilde {\underline {\theta }}^j\wedge \underline {a}^j\in \Sigma _j(c_0,\rho )$
,
![]() $1\leq j\leq n$
, one has
$1\leq j\leq n$
, one has
 $$ \begin{align*}B_{\rho}\bigg(x+\bigg(\log \frac{r_{\underline{b}^1}^{\tilde{\underline{\theta}}^1}}{r_{\underline{b}^n}^{\tilde{\underline{\theta}}^n}},\ldots,\log \frac{r_{\underline{b}^{n-1}}^{\tilde{\underline{\theta}}^{n-1}}}{r_{\underline{b}^n}^{\tilde{\underline{\theta}}^n}},v_{\underline{b}^1}^{\tilde{\underline{\theta}}^1},\ldots,v_{\underline{b}^n}^{\tilde{\underline{\theta}}^n}\bigg)\bigg)\subset B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'}),\end{align*} $$
$$ \begin{align*}B_{\rho}\bigg(x+\bigg(\log \frac{r_{\underline{b}^1}^{\tilde{\underline{\theta}}^1}}{r_{\underline{b}^n}^{\tilde{\underline{\theta}}^n}},\ldots,\log \frac{r_{\underline{b}^{n-1}}^{\tilde{\underline{\theta}}^{n-1}}}{r_{\underline{b}^n}^{\tilde{\underline{\theta}}^n}},v_{\underline{b}^1}^{\tilde{\underline{\theta}}^1},\ldots,v_{\underline{b}^n}^{\tilde{\underline{\theta}}^n}\bigg)\bigg)\subset B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'}),\end{align*} $$
where
![]() $\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^n)$
,
$\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^n)$
,
![]() $\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)$
,
$\unicode{x3bb} =(\underline {a}^1,\ldots ,\underline {a}^n)$
,
![]() $a_{\unicode{x3bb} }^{\unicode{x3bb} '}=(\log ({r_{\underline {b}^1}^{\underline {\theta }^1}}/{r_{\underline {b}^n}^{\underline {\theta }^n}}),\ldots ,\log ({r_{\underline {b}^{n-1}}^{\underline {\theta }^{n-1}}}/ {r_{\underline {b}^n}^{\underline {\theta }^n}}), v_{\underline {b}^1}^{\underline {\theta }^1},\ldots ,v_{\underline {b}^n}^{\underline {\theta }^n})$
for some
$a_{\unicode{x3bb} }^{\unicode{x3bb} '}=(\log ({r_{\underline {b}^1}^{\underline {\theta }^1}}/{r_{\underline {b}^n}^{\underline {\theta }^n}}),\ldots ,\log ({r_{\underline {b}^{n-1}}^{\underline {\theta }^{n-1}}}/ {r_{\underline {b}^n}^{\underline {\theta }^n}}), v_{\underline {b}^1}^{\underline {\theta }^1},\ldots ,v_{\underline {b}^n}^{\underline {\theta }^n})$
for some
![]() $\underline {\theta }^j$
ending in
$\underline {\theta }^j$
ending in
![]() $\underline {a}^j$
,
$\underline {a}^j$
,
![]() $1\leq j\leq n$
. This is accomplished by taking
$1\leq j\leq n$
. This is accomplished by taking
![]() $\Delta _1$
big. More precisely, since
$\Delta _1$
big. More precisely, since
for all
![]() $1\leq j\leq n$
, for some constant
$1\leq j\leq n$
, for some constant
![]() $\tilde {C}$
only depending on
$\tilde {C}$
only depending on
![]() $c_0$
, we can conclude that
$c_0$
, we can conclude that
![]() $|\! \log r_{\underline {b}}^{\underline {\theta }^j}-\log r_{\underline {b}}^{\tilde {\underline {\theta }}^j}|\leq \tilde {C}_1 \rho ,\,\,\,| v_{\underline {b}}^{\underline {\theta }^j}-v_{\underline {b}}^{\tilde {\underline {\theta }}^j}|\leq \tilde {C}_1 \rho $
for all
$|\! \log r_{\underline {b}}^{\underline {\theta }^j}-\log r_{\underline {b}}^{\tilde {\underline {\theta }}^j}|\leq \tilde {C}_1 \rho ,\,\,\,| v_{\underline {b}}^{\underline {\theta }^j}-v_{\underline {b}}^{\tilde {\underline {\theta }}^j}|\leq \tilde {C}_1 \rho $
for all
![]() $1\leq j\leq n$
, for some constant
$1\leq j\leq n$
, for some constant
![]() $\tilde {C}_1$
only depending on
$\tilde {C}_1$
only depending on
![]() $c_0$
. Therefore, imposing
$c_0$
. Therefore, imposing
would be sufficient to guarantee the second property.
(iii) By equation (14), choosing
![]() $c_1$
,
$c_1$
,
![]() $\rho _0$
small such that
$\rho _0$
small such that
where
![]() $C_1$
is a constant such that
$C_1$
is a constant such that
![]() $p^{\unicode{x3bb} }\geq C_1 (\#\Lambda )^{-1}\ \text { for all } \unicode{x3bb} \in \Lambda $
, implies that
$p^{\unicode{x3bb} }\geq C_1 (\#\Lambda )^{-1}\ \text { for all } \unicode{x3bb} \in \Lambda $
, implies that
 $$ \begin{align*}\sum_{\unicode{x3bb} \in\Lambda} p^{\unicode{x3bb}}\nu(F^*(\unicode{x3bb}))\geq \bigg(1-\frac{C_1T_1}{2(T_1+T_2)}\bigg)\nu(J_r).\end{align*} $$
$$ \begin{align*}\sum_{\unicode{x3bb} \in\Lambda} p^{\unicode{x3bb}}\nu(F^*(\unicode{x3bb}))\geq \bigg(1-\frac{C_1T_1}{2(T_1+T_2)}\bigg)\nu(J_r).\end{align*} $$
Let
![]() $A=\{\unicode{x3bb} : \nu (F^*(\unicode{x3bb} ))\geq \nu (J_r)/2\}$
, and hence,
$A=\{\unicode{x3bb} : \nu (F^*(\unicode{x3bb} ))\geq \nu (J_r)/2\}$
, and hence,
 $$ \begin{align*} \bigg(1-\frac{C_1T_1}{2(T_1+T_2)}\bigg)\nu(J_r) &\leq \sum_{\unicode{x3bb} \in A} p^{\unicode{x3bb}}\nu(F^*(\unicode{x3bb})) + \sum_{\unicode{x3bb} \in \Lambda\setminus A} p^{\unicode{x3bb}}\nu(F^*(\unicode{x3bb}))\\ &\leq \nu(J_r) \sum_{\unicode{x3bb} \in A} p^{\unicode{x3bb}} + \frac{\nu(J_r)}{2} \sum_{\unicode{x3bb} \in \Lambda\setminus A} p^{\unicode{x3bb}}\\ &= \nu(J_r)-\frac{\nu(J_r)}{2} \sum_{\unicode{x3bb} \in \Lambda\setminus A} p^{\unicode{x3bb}}. \end{align*} $$
$$ \begin{align*} \bigg(1-\frac{C_1T_1}{2(T_1+T_2)}\bigg)\nu(J_r) &\leq \sum_{\unicode{x3bb} \in A} p^{\unicode{x3bb}}\nu(F^*(\unicode{x3bb})) + \sum_{\unicode{x3bb} \in \Lambda\setminus A} p^{\unicode{x3bb}}\nu(F^*(\unicode{x3bb}))\\ &\leq \nu(J_r) \sum_{\unicode{x3bb} \in A} p^{\unicode{x3bb}} + \frac{\nu(J_r)}{2} \sum_{\unicode{x3bb} \in \Lambda\setminus A} p^{\unicode{x3bb}}\\ &= \nu(J_r)-\frac{\nu(J_r)}{2} \sum_{\unicode{x3bb} \in \Lambda\setminus A} p^{\unicode{x3bb}}. \end{align*} $$
From this inequality, we get
![]() $({C_1}/{2})({\#(\Lambda \setminus A)}/{\#\Lambda })\leq \tfrac 12 \sum _{\unicode{x3bb} \in \Lambda \setminus A} p^{\unicode{x3bb} } \leq {C_1T_1}/ {2(T_1+T_2)}.$
Finally, this implies
$({C_1}/{2})({\#(\Lambda \setminus A)}/{\#\Lambda })\leq \tfrac 12 \sum _{\unicode{x3bb} \in \Lambda \setminus A} p^{\unicode{x3bb} } \leq {C_1T_1}/ {2(T_1+T_2)}.$
Finally, this implies
![]() $\# A>(T_2/(T_1+T_2))\#\Lambda $
, as we wanted.
$\# A>(T_2/(T_1+T_2))\#\Lambda $
, as we wanted.
Proof of Lemma 4.1
Choose
![]() $c_3>0$
,
$c_3>0$
,
![]() $\epsilon _2>0$
small such that
$\epsilon _2>0$
small such that
 $$ \begin{align} \bigg( c_3+ C_2^{-1}\frac{\epsilon_2}{\epsilon_1}\bigg)\rho^{-(d_1+\cdots+d_n)}<(1-\tau)N_{\omega(\unicode{x3bb})}\quad\text{for all } \unicode{x3bb} \in \Lambda, \end{align} $$
$$ \begin{align} \bigg( c_3+ C_2^{-1}\frac{\epsilon_2}{\epsilon_1}\bigg)\rho^{-(d_1+\cdots+d_n)}<(1-\tau)N_{\omega(\unicode{x3bb})}\quad\text{for all } \unicode{x3bb} \in \Lambda, \end{align} $$
where
![]() $C_2$
is a constant such that
$C_2$
is a constant such that
![]() $p^{\unicode{x3bb} }\geq C_2 \rho ^{d_1+\cdots +d_n}\ \text { for all } \unicode{x3bb} \in \Lambda $
. We suppose that
$p^{\unicode{x3bb} }\geq C_2 \rho ^{d_1+\cdots +d_n}\ \text { for all } \unicode{x3bb} \in \Lambda $
. We suppose that
![]() $c_1$
,
$c_1$
,
![]() $\rho _0$
are small enough such that
$\rho _0$
are small enough such that
We will proceed by induction following the scheme
For the base case, equation (13) for
![]() $m=0$
, notice that
$m=0$
, notice that
![]() $V_{\Delta \rho }(E_0(\unicode{x3bb} ))\subset J_{r+\Delta \rho }\setminus F(\unicode{x3bb} ).$
Therefore,
$V_{\Delta \rho }(E_0(\unicode{x3bb} ))\subset J_{r+\Delta \rho }\setminus F(\unicode{x3bb} ).$
Therefore,
Now we prove ‘equation (13) for
![]() $m\ \Rightarrow $
equation (12) for m’: define
$m\ \Rightarrow $
equation (12) for m’: define
![]() $\Lambda _b=\{\unicode{x3bb} \in \Lambda : \nu (V_{\Delta \rho }(E_m(\unicode{x3bb} )))<\epsilon _1\}$
,
$\Lambda _b=\{\unicode{x3bb} \in \Lambda : \nu (V_{\Delta \rho }(E_m(\unicode{x3bb} )))<\epsilon _1\}$
,
![]() $A(\unicode{x3bb} )=E_m(\unicode{x3bb} )$
for
$A(\unicode{x3bb} )=E_m(\unicode{x3bb} )$
for
![]() $\unicode{x3bb} \in \Lambda _b$
and
$\unicode{x3bb} \in \Lambda _b$
and
![]() $A(\unicode{x3bb} )=\emptyset $
otherwise. We will show that
$A(\unicode{x3bb} )=\emptyset $
otherwise. We will show that
![]() $\tilde {E}_m(\unicode{x3bb} )\cap J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }\subset \hat {A}(\unicode{x3bb} ).$
Here
$\tilde {E}_m(\unicode{x3bb} )\cap J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }\subset \hat {A}(\unicode{x3bb} ).$
Here
![]() $\hat {A}(\unicode{x3bb} )$
is the set from Corollary 4.1, that is, the
$\hat {A}(\unicode{x3bb} )$
is the set from Corollary 4.1, that is, the
![]() $x\in J$
such that
$x\in J$
such that
 $$ \begin{align*}\frac{1}{\# \Lambda_{\omega(\unicode{x3bb})}}\cdot \#\{\unicode{x3bb}'\in \Lambda_{\omega(\unicode{x3bb})}:B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset J\setminus A(\unicode{x3bb}') \} \leq 1-\tau.\end{align*} $$
$$ \begin{align*}\frac{1}{\# \Lambda_{\omega(\unicode{x3bb})}}\cdot \#\{\unicode{x3bb}'\in \Lambda_{\omega(\unicode{x3bb})}:B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset J\setminus A(\unicode{x3bb}') \} \leq 1-\tau.\end{align*} $$
Using equation (17) gives
![]() $\epsilon _2>\sum _{\unicode{x3bb} \in \Lambda }p^{\unicode{x3bb} }\nu (V_{\Delta \rho }(E_m(\unicode{x3bb} )))\geq C_2 \rho ^{d_1+\cdots +d_n}\epsilon _1 \#(\Lambda \setminus \Lambda _b),$
and hence,
$\epsilon _2>\sum _{\unicode{x3bb} \in \Lambda }p^{\unicode{x3bb} }\nu (V_{\Delta \rho }(E_m(\unicode{x3bb} )))\geq C_2 \rho ^{d_1+\cdots +d_n}\epsilon _1 \#(\Lambda \setminus \Lambda _b),$
and hence,
Let
![]() $x\in \tilde {E}_m(\unicode{x3bb} )\cap J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }$
, using the last inequality, equation (16), and the fact that
$x\in \tilde {E}_m(\unicode{x3bb} )\cap J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }$
, using the last inequality, equation (16), and the fact that
![]() $a_{\unicode{x3bb} }^{\unicode{x3bb} '}\in J_{2\log (c \tilde {c}_0)}\ \text { for all } \unicode{x3bb} , \unicode{x3bb} '\in \Lambda $
, we have
$a_{\unicode{x3bb} }^{\unicode{x3bb} '}\in J_{2\log (c \tilde {c}_0)}\ \text { for all } \unicode{x3bb} , \unicode{x3bb} '\in \Lambda $
, we have
 $$ \begin{align*} \#\{\unicode{x3bb}'\in \Lambda_{\omega(\unicode{x3bb})}:B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})&\subset J\setminus A(\unicode{x3bb}') \} \\ &\leq \#\{\unicode{x3bb}'\in \Lambda_b:B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset J\setminus E_m(\varphi(\unicode{x3bb}')) \}\\ &\quad+ \#(\Lambda\setminus \Lambda_b)\\ &\leq \#\{\unicode{x3bb}'\in \Lambda':B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset J_r\setminus E_m(\varphi(\unicode{x3bb}'))\}\\ &\quad+C_2^{-1}\frac{\epsilon_2}{\epsilon_1}\rho^{-(d_1+\cdots+d_n)}\\ &\leq (c_3+C_2^{-1}\frac{\epsilon_2}{\epsilon_1})\rho^{-(d_1+\cdots+d_n)}\\ &<(1-\tau)N_{\omega(\unicode{x3bb})}. \end{align*} $$
$$ \begin{align*} \#\{\unicode{x3bb}'\in \Lambda_{\omega(\unicode{x3bb})}:B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})&\subset J\setminus A(\unicode{x3bb}') \} \\ &\leq \#\{\unicode{x3bb}'\in \Lambda_b:B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset J\setminus E_m(\varphi(\unicode{x3bb}')) \}\\ &\quad+ \#(\Lambda\setminus \Lambda_b)\\ &\leq \#\{\unicode{x3bb}'\in \Lambda':B_{\Delta_1 \rho}(x+a_{\unicode{x3bb}}^{\unicode{x3bb}'})\subset J_r\setminus E_m(\varphi(\unicode{x3bb}'))\}\\ &\quad+C_2^{-1}\frac{\epsilon_2}{\epsilon_1}\rho^{-(d_1+\cdots+d_n)}\\ &\leq (c_3+C_2^{-1}\frac{\epsilon_2}{\epsilon_1})\rho^{-(d_1+\cdots+d_n)}\\ &<(1-\tau)N_{\omega(\unicode{x3bb})}. \end{align*} $$
Hence,
![]() $x\in \hat {A}(\unicode{x3bb} )$
, and we have shown
$x\in \hat {A}(\unicode{x3bb} )$
, and we have shown
![]() $\tilde {E}_m(\unicode{x3bb} )\cap J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }\subset \hat {A}(\unicode{x3bb} ).$
Clearly the family
$\tilde {E}_m(\unicode{x3bb} )\cap J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }\subset \hat {A}(\unicode{x3bb} ).$
Clearly the family
![]() $A(\unicode{x3bb} )$
satisfies the hypothesis of Corollary 4.1, that is,
$A(\unicode{x3bb} )$
satisfies the hypothesis of Corollary 4.1, that is,
![]() $\nu (V_{\Delta \rho }(A(\unicode{x3bb} )))<\epsilon _1$
. Using the corollary gives
$\nu (V_{\Delta \rho }(A(\unicode{x3bb} )))<\epsilon _1$
. Using the corollary gives
 $$ \begin{align} \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\tilde{E}_m(\unicode{x3bb})\cap J_{r-2\log (c\tilde{c}_0)-\Delta_1\rho}))&\leq \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\hat{A}(\unicode{x3bb})))\nonumber \\ &\leq k_4 \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(A(\unicode{x3bb})))\nonumber \\ &\leq k_4\sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}))). \end{align} $$
$$ \begin{align} \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\tilde{E}_m(\unicode{x3bb})\cap J_{r-2\log (c\tilde{c}_0)-\Delta_1\rho}))&\leq \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\hat{A}(\unicode{x3bb})))\nonumber \\ &\leq k_4 \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(A(\unicode{x3bb})))\nonumber \\ &\leq k_4\sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}))). \end{align} $$
Now we estimate
![]() $\tilde {E}_m(\unicode{x3bb} )$
outside of
$\tilde {E}_m(\unicode{x3bb} )$
outside of
![]() $J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }$
. Assume that
$J_{r-2\log (c\tilde {c}_0)-\Delta _1\rho }$
. Assume that
![]() $\rho _0$
is small enough such that
$\rho _0$
is small enough such that
![]() $2\Delta \rho <\tfrac 14\log (c\tilde {c}_0)$
,
$2\Delta \rho <\tfrac 14\log (c\tilde {c}_0)$
,
![]() $\Delta _1 \rho <\tfrac 14\log (c\tilde {c}_0)$
. By equation (11), for every
$\Delta _1 \rho <\tfrac 14\log (c\tilde {c}_0)$
. By equation (11), for every
![]() $j=1,\ldots ,n$
, there exist intervals
$j=1,\ldots ,n$
, there exist intervals
 $$ \begin{align*} I_j^- &\subset [-r,-r+\delta^{-1}(9\log (c\tilde{c}_0)+2\Delta \rho)]\subset [-r,r],\\ I_j^+ &\subset [r-\delta^{-1}(9\log (c\tilde{c}_0)+2\Delta \rho),r]\subset [-r,r], \end{align*} $$
$$ \begin{align*} I_j^- &\subset [-r,-r+\delta^{-1}(9\log (c\tilde{c}_0)+2\Delta \rho)]\subset [-r,r],\\ I_j^+ &\subset [r-\delta^{-1}(9\log (c\tilde{c}_0)+2\Delta \rho),r]\subset [-r,r], \end{align*} $$
with
![]() $\mathrm {diam}(I_j^-)=\mathrm {diam}(I_j^+)=9\log (c\tilde {c}_0)$
such that
$\mathrm {diam}(I_j^-)=\mathrm {diam}(I_j^+)=9\log (c\tilde {c}_0)$
such that
 $$ \begin{align*} \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb})\cap J^-_j))&\leq \delta \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb}))),\\ \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb})\cap J^+_j))&\leq \delta \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb}))), \end{align*} $$
$$ \begin{align*} \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb})\cap J^-_j))&\leq \delta \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb}))),\\ \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb})\cap J^+_j))&\leq \delta \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta \rho}(E_m(\unicode{x3bb}))), \end{align*} $$
where
![]() $J^{+(-)}_j=\{(t_1,\ldots ,t_{n-1},v)\in J_r:t_j\in I^{+(-)}_j\}$
.
$J^{+(-)}_j=\{(t_1,\ldots ,t_{n-1},v)\in J_r:t_j\in I^{+(-)}_j\}$
.
For every pair
![]() $(A,B)$
such that
$(A,B)$
such that
![]() $A,B \subset \{1,\ldots ,n-1\}$
and
$A,B \subset \{1,\ldots ,n-1\}$
and
![]() $A\cap B=\emptyset $
, consider
$A\cap B=\emptyset $
, consider
![]() $y_{A,B}=(t_1(A,B),\ldots ,t_{n-1}(A,B),0)\in J$
given by
$y_{A,B}=(t_1(A,B),\ldots ,t_{n-1}(A,B),0)\in J$
given by
 $$ \begin{align*} t_j(A,B)= \begin{cases} -r+\log(c\tilde{c}_0) & \mbox{if } j \in A, \\ r-\log(c\tilde{c}_0) & \mbox{if } j \in B, \\ 0 & \mbox{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} t_j(A,B)= \begin{cases} -r+\log(c\tilde{c}_0) & \mbox{if } j \in A, \\ r-\log(c\tilde{c}_0) & \mbox{if } j \in B, \\ 0 & \mbox{otherwise}. \end{cases} \end{align*} $$
We also define sets
![]() $\tilde {J}_{A,B}, J_{A,B} \subset J$
in the following way:
$\tilde {J}_{A,B}, J_{A,B} \subset J$
in the following way:
 $$ \begin{align*} J_{A,B}=\{(t_1,\ldots,t_{n-1},v)\in J_{r}:t_j\in I^{+}_j\,& \mbox{if } j\in B, t_j\in I^{-}_j\, \mbox{if } j\in A\},& \\ \tilde{J}_{A,B}=\{(t_1,\ldots,t_{n-1},v)\in J_r:t_j\in \tilde{I}^{+}_j\,& \mbox{if } j\in B, t_j\in \tilde{I}^{-}_j\, \mbox{if } j\in A\}, \end{align*} $$
$$ \begin{align*} J_{A,B}=\{(t_1,\ldots,t_{n-1},v)\in J_{r}:t_j\in I^{+}_j\,& \mbox{if } j\in B, t_j\in I^{-}_j\, \mbox{if } j\in A\},& \\ \tilde{J}_{A,B}=\{(t_1,\ldots,t_{n-1},v)\in J_r:t_j\in \tilde{I}^{+}_j\,& \mbox{if } j\in B, t_j\in \tilde{I}^{-}_j\, \mbox{if } j\in A\}, \end{align*} $$
where the interval
![]() $\tilde {I}^{u}_j$
has the same center as
$\tilde {I}^{u}_j$
has the same center as
![]() $I^{u}_j$
and has length
$I^{u}_j$
and has length
![]() $2\log (c\tilde {c}_0)$
; here
$2\log (c\tilde {c}_0)$
; here
![]() $u=+$
or
$u=+$
or
![]() $-$
.
$-$
.
Fix
![]() $\unicode{x3bb} \in \Lambda $
. From the choice of
$\unicode{x3bb} \in \Lambda $
. From the choice of
![]() $\rho _1$
and
$\rho _1$
and
![]() $c_0$
, we know that there is
$c_0$
, we know that there is
![]() $\unicode{x3bb} _{A,B}\in \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}$
such that
$\unicode{x3bb} _{A,B}\in \Sigma _1^\textit{fin}\times \cdots \times \Sigma _n^\textit{fin}$
such that
![]() $y_{A,B}+a_{\unicode{x3bb} }^{\unicode{x3bb} _{A,B}}\in \tilde {J}_{A,B},$
and
$y_{A,B}+a_{\unicode{x3bb} }^{\unicode{x3bb} _{A,B}}\in \tilde {J}_{A,B},$
and
![]() $\unicode{x3bb} _{A,B}\unicode{x3bb} '\in \Lambda '\ \text { for all } \unicode{x3bb} '\in \Lambda _{\omega (\unicode{x3bb} _{A,B})}$
.
$\unicode{x3bb} _{A,B}\unicode{x3bb} '\in \Lambda '\ \text { for all } \unicode{x3bb} '\in \Lambda _{\omega (\unicode{x3bb} _{A,B})}$
.
Let
![]() $x\in V_{\Delta \rho }(\tilde {E}_m(\unicode{x3bb} )\cap J_r\setminus J_{r-2\log (c\tilde {c}_0)-\Delta _1 \rho }),$
then there is
$x\in V_{\Delta \rho }(\tilde {E}_m(\unicode{x3bb} )\cap J_r\setminus J_{r-2\log (c\tilde {c}_0)-\Delta _1 \rho }),$
then there is
![]() $y\in \tilde {E}_m(\unicode{x3bb} )\cap J_r\setminus J_{r-2\log (c\tilde {c}_0)-\Delta _1 \rho }$
,
$y\in \tilde {E}_m(\unicode{x3bb} )\cap J_r\setminus J_{r-2\log (c\tilde {c}_0)-\Delta _1 \rho }$
,
![]() $y\in B_{\Delta \rho }(x)$
, and for y, we have
$y\in B_{\Delta \rho }(x)$
, and for y, we have
Write
![]() $y=(t_1,\ldots ,t_{n-1},v)$
and consider the sets
$y=(t_1,\ldots ,t_{n-1},v)$
and consider the sets
 $$ \begin{align*} A&=\{j\in [1,n-1]\cap \mathbb{Z}: t_j<-r+2\log (c\tilde{c}_0)+\Delta_1 \rho\},\\ B&=\{j\in [1,n-1]\cap \mathbb{Z}: t_j>r-2\log (c\tilde{c}_0)-\Delta_1 \rho\}. \end{align*} $$
$$ \begin{align*} A&=\{j\in [1,n-1]\cap \mathbb{Z}: t_j<-r+2\log (c\tilde{c}_0)+\Delta_1 \rho\},\\ B&=\{j\in [1,n-1]\cap \mathbb{Z}: t_j>r-2\log (c\tilde{c}_0)-\Delta_1 \rho\}. \end{align*} $$
Since
![]() $y\notin J_{r-2\log (c\tilde {c}_0)-\Delta _1 \rho }$
, we know that
$y\notin J_{r-2\log (c\tilde {c}_0)-\Delta _1 \rho }$
, we know that
![]() $A\cup B\neq \emptyset $
and we can consider
$A\cup B\neq \emptyset $
and we can consider
![]() $\unicode{x3bb} _{A,B}$
. Given that
$\unicode{x3bb} _{A,B}$
. Given that
![]() $\#\Lambda _{\omega (\unicode{x3bb} _{A,B})}\geq L^{-1}\rho ^{-(d_1+\cdots +d_n)}$
, we conclude that
$\#\Lambda _{\omega (\unicode{x3bb} _{A,B})}\geq L^{-1}\rho ^{-(d_1+\cdots +d_n)}$
, we conclude that

where we are assuming that
![]() $c_3<L^{-1}/2$
. Notice that
$c_3<L^{-1}/2$
. Notice that
![]() $B_{\Delta _1\rho }(y+a_{\unicode{x3bb} }^{\unicode{x3bb} _{A,B}\unicode{x3bb} '})\cap J_r\subset J_{A,B}\ \text { for all } \unicode{x3bb} '\in \Lambda _{\omega (\unicode{x3bb} _0)}$
; therefore,
$B_{\Delta _1\rho }(y+a_{\unicode{x3bb} }^{\unicode{x3bb} _{A,B}\unicode{x3bb} '})\cap J_r\subset J_{A,B}\ \text { for all } \unicode{x3bb} '\in \Lambda _{\omega (\unicode{x3bb} _0)}$
; therefore,
Hence,
![]() $V_{\Delta \rho }(\tilde {E}_n(\unicode{x3bb} )\cap J_r\setminus J_{r-2\log (c\tilde {c}_0)-\Delta _1 \rho })$
is contained in
$V_{\Delta \rho }(\tilde {E}_n(\unicode{x3bb} )\cap J_r\setminus J_{r-2\log (c\tilde {c}_0)-\Delta _1 \rho })$
is contained in

where the first sum is over all pairs
![]() $(A,B)$
such that
$(A,B)$
such that
![]() $A,B\subset \{1,\ldots ,n\}$
,
$A,B\subset \{1,\ldots ,n\}$
,
![]() $A\cap B=\emptyset $
,
$A\cap B=\emptyset $
,
![]() $A\cup B\neq \emptyset $
. Now using Chebyshev’s inequality, we get
$A\cup B\neq \emptyset $
. Now using Chebyshev’s inequality, we get

where
![]() $C_4>0$
is a constant, only depending on
$C_4>0$
is a constant, only depending on
![]() $\tilde {c}_0$
, such that
$\tilde {c}_0$
, such that
Now we will sum over
![]() $\unicode{x3bb} $
. By the definition of
$\unicode{x3bb} $
. By the definition of
![]() $\Delta $
, we know that
$\Delta $
, we know that
![]() $(1+{\Delta _1}/{\Delta })^{2n-1}<k_1^{-1},$
and using
$(1+{\Delta _1}/{\Delta })^{2n-1}<k_1^{-1},$
and using
![]() $p^{\unicode{x3bb} '}\geq C_2\rho ^{d_1+\cdots +d_n}$
, we get
$p^{\unicode{x3bb} '}\geq C_2\rho ^{d_1+\cdots +d_n}$
, we get
 $$ \begin{align*} &\sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\tilde{E}_m(\unicode{x3bb})\cap J_r\setminus J_{r-2\log (c\tilde{c}_0)-\Delta_1 \rho}))\\ &\quad\leq 2\bigg(1+\frac{\Delta_1}{\Delta}\bigg)^{2n-1} C_4 L\rho^{d_1+\cdots+d_n}\sum_{(A,B)} \sum_{\unicode{x3bb}'\in \Lambda}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}')\cap J_{A,B}))\\ &\quad\leq 2k_1^{-1}C_4L\rho^{d_1+\cdots+d_n}\frac{1}{C_2\rho^{d_1+\cdots+d^{\prime}_n}}\sum_{(A,B)} \sum_{\unicode{x3bb}'\in \Lambda}p^{\unicode{x3bb}'}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}')\cap J_{A,B}))\\ &\quad\leq 2\cdot 3^n k_1^{-1} LC_2^{-1}C_4\delta \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}))). \end{align*} $$
$$ \begin{align*} &\sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\tilde{E}_m(\unicode{x3bb})\cap J_r\setminus J_{r-2\log (c\tilde{c}_0)-\Delta_1 \rho}))\\ &\quad\leq 2\bigg(1+\frac{\Delta_1}{\Delta}\bigg)^{2n-1} C_4 L\rho^{d_1+\cdots+d_n}\sum_{(A,B)} \sum_{\unicode{x3bb}'\in \Lambda}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}')\cap J_{A,B}))\\ &\quad\leq 2k_1^{-1}C_4L\rho^{d_1+\cdots+d_n}\frac{1}{C_2\rho^{d_1+\cdots+d^{\prime}_n}}\sum_{(A,B)} \sum_{\unicode{x3bb}'\in \Lambda}p^{\unicode{x3bb}'}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}')\cap J_{A,B}))\\ &\quad\leq 2\cdot 3^n k_1^{-1} LC_2^{-1}C_4\delta \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}))). \end{align*} $$
Putting this inequality together with (18) gives
 $$ \begin{align*} \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\tilde{E}_m(\unicode{x3bb})))&\leq (k_4+2\cdot 3^n k_1^{-1} LC_2^{-1}C_4\delta)\sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb})))\\ &\leq k_5 \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}))), \end{align*} $$
$$ \begin{align*} \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\tilde{E}_m(\unicode{x3bb})))&\leq (k_4+2\cdot 3^n k_1^{-1} LC_2^{-1}C_4\delta)\sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb})))\\ &\leq k_5 \sum_{\unicode{x3bb}\in \Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_m(\unicode{x3bb}))), \end{align*} $$
which is equation (12) for m. Here we have used equation (8) where
![]() $\delta $
was chosen.
$\delta $
was chosen.
To finish, we prove ‘equation (13) for m and equation (12) for
![]() $m\ \Rightarrow $
equation (13) for
$m\ \Rightarrow $
equation (13) for
![]() $m+1$
’. Since
$m+1$
’. Since
![]() $E_{m+1}(\unicode{x3bb} )=E_0(\unicode{x3bb} )\cup \tilde {E}_m(\unicode{x3bb} )$
and
$E_{m+1}(\unicode{x3bb} )=E_0(\unicode{x3bb} )\cup \tilde {E}_m(\unicode{x3bb} )$
and
![]() $\nu (V_{\Delta \rho }(E_0(\unicode{x3bb} )))\leq \nu (J_{r+\Delta \rho }\setminus J_r)+c_1$
, we get
$\nu (V_{\Delta \rho }(E_0(\unicode{x3bb} )))\leq \nu (J_{r+\Delta \rho }\setminus J_r)+c_1$
, we get
 $$ \begin{align*} \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_{m+1}(\unicode{x3bb})))&\leq \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_0(\unicode{x3bb})))+\sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\tilde{E}_{m}(\unicode{x3bb})))\\ &\leq \nu(J_{r+\Delta \rho}\setminus J_r)+c_1+k_5\sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_{m}(\unicode{x3bb})))\\ &\leq \nu(J_{r+\Delta \rho}\setminus J_r)+c_1+k_5\frac{\nu(J_{r+\Delta \rho}\setminus J_r)+c_1}{1-k_5}\\ &=\frac{\nu(J_{r+\Delta \rho}\setminus J_r)+c_1}{1-k_5}.\\[-3.7pc] \end{align*} $$
$$ \begin{align*} \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_{m+1}(\unicode{x3bb})))&\leq \sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_0(\unicode{x3bb})))+\sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(\tilde{E}_{m}(\unicode{x3bb})))\\ &\leq \nu(J_{r+\Delta \rho}\setminus J_r)+c_1+k_5\sum_{\unicode{x3bb}\in\Lambda}p^{\unicode{x3bb}}\nu(V_{\Delta\rho}(E_{m}(\unicode{x3bb})))\\ &\leq \nu(J_{r+\Delta \rho}\setminus J_r)+c_1+k_5\frac{\nu(J_{r+\Delta \rho}\setminus J_r)+c_1}{1-k_5}\\ &=\frac{\nu(J_{r+\Delta \rho}\setminus J_r)+c_1}{1-k_5}.\\[-3.7pc] \end{align*} $$
4.3 Proof of hypothesis on Proposition 4.1
In this subsection, we prove that there exist
![]() $0<k_0<1$
,
$0<k_0<1$
,
![]() $\Delta _0>0$
such that
$\Delta _0>0$
such that
![]() $\|T_{\xi }\|\leq k_0$
for all
$\|T_{\xi }\|\leq k_0$
for all
![]() $|\xi |\in [1,\Delta _0\rho ^{-1}]$
, and these constants does not depend on
$|\xi |\in [1,\Delta _0\rho ^{-1}]$
, and these constants does not depend on
![]() $\rho $
. Remember that the operator
$\rho $
. Remember that the operator
![]() $T_{\xi }:\mathbb {C}^{\Lambda }\to \mathbb {C}^{\Lambda }$
is given by
$T_{\xi }:\mathbb {C}^{\Lambda }\to \mathbb {C}^{\Lambda }$
is given by
![]() $T_{\xi }((z_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda })=(w_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda }$
, where
$T_{\xi }((z_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda })=(w_{\unicode{x3bb} })_{\unicode{x3bb} \in \Lambda }$
, where
![]() $w_{\unicode{x3bb} }=\sum _{\unicode{x3bb} '\in \Lambda } p_{\unicode{x3bb} }^{\unicode{x3bb} '}\xi (a_{\unicode{x3bb} }^{\unicode{x3bb} '})z_{\unicode{x3bb} '}.$
Notice that
$w_{\unicode{x3bb} }=\sum _{\unicode{x3bb} '\in \Lambda } p_{\unicode{x3bb} }^{\unicode{x3bb} '}\xi (a_{\unicode{x3bb} }^{\unicode{x3bb} '})z_{\unicode{x3bb} '}.$
Notice that
![]() $\mathbb {C}^{\Lambda }$
can be decomposed in two ways:
$\mathbb {C}^{\Lambda }$
can be decomposed in two ways:
 $$ \begin{align*}\mathbb{C}^{\Lambda}=\bigoplus_{i\in A} \mathbb{C}^{\Lambda_i},\,\,\,\mathbb{C}^{\Lambda}=\bigoplus_{j\in A} \mathbb{C}^{\Lambda^j},\end{align*} $$
$$ \begin{align*}\mathbb{C}^{\Lambda}=\bigoplus_{i\in A} \mathbb{C}^{\Lambda_i},\,\,\,\mathbb{C}^{\Lambda}=\bigoplus_{j\in A} \mathbb{C}^{\Lambda^j},\end{align*} $$
and the operator
![]() $T_{\xi }$
sends
$T_{\xi }$
sends
![]() $\mathbb {C}^{\Lambda _i}$
into
$\mathbb {C}^{\Lambda _i}$
into
![]() $\mathbb {C}^{\Lambda ^i}$
. Let
$\mathbb {C}^{\Lambda ^i}$
. Let
![]() $\|\cdot \|_i$
,
$\|\cdot \|_i$
,
![]() $\|\cdot \|^{j}$
be the restriction to
$\|\cdot \|^{j}$
be the restriction to
![]() $\mathbb {C}^{\Lambda _i}$
,
$\mathbb {C}^{\Lambda _i}$
,
![]() $\mathbb {C}^{\Lambda ^j}$
, respectively, of the norm
$\mathbb {C}^{\Lambda ^j}$
, respectively, of the norm
![]() $\|\cdot \|$
on
$\|\cdot \|$
on
![]() $\Lambda $
. Note that
$\Lambda $
. Note that
 $$ \begin{align*}\|z\|^2=\sum_{i\in A}\|\pi_i(z)\|_i^2=\sum_{j\in A}(\|\pi^j(z)\|^j)^2 \text{ for all } z\in \mathbb{C}^{\Lambda},\end{align*} $$
$$ \begin{align*}\|z\|^2=\sum_{i\in A}\|\pi_i(z)\|_i^2=\sum_{j\in A}(\|\pi^j(z)\|^j)^2 \text{ for all } z\in \mathbb{C}^{\Lambda},\end{align*} $$
where
![]() $\pi _i:\mathbb {C}^{\Lambda }\to \mathbb {C}^{\Lambda _i}$
,
$\pi _i:\mathbb {C}^{\Lambda }\to \mathbb {C}^{\Lambda _i}$
,
![]() $\pi ^j:\mathbb {C}^{\Lambda }\to \mathbb {C}^{\Lambda ^j}$
are the projections given by the decompositions. This implies that
$\pi ^j:\mathbb {C}^{\Lambda }\to \mathbb {C}^{\Lambda ^j}$
are the projections given by the decompositions. This implies that
![]() $\|T_{\xi }\|\leq k_0$
if and only if
$\|T_{\xi }\|\leq k_0$
if and only if
![]() $\|T_{\xi }|_{\mathbb {C}^{\Lambda _i}}\|\leq k_0\ \text { for all } i\in A$
, where
$\|T_{\xi }|_{\mathbb {C}^{\Lambda _i}}\|\leq k_0\ \text { for all } i\in A$
, where
![]() $T_{\xi }|_{\mathbb {C}^{\Lambda _i}}$
is the restriction
$T_{\xi }|_{\mathbb {C}^{\Lambda _i}}$
is the restriction
![]() $T_{\xi }|_{\mathbb {C}^{\Lambda _i}}:(\mathbb {C}^{\Lambda _i},\|\cdot \|_i)\to (\mathbb {C}^{\Lambda ^i},\|\cdot \|^i).$
We start by supposing that there exist
$T_{\xi }|_{\mathbb {C}^{\Lambda _i}}:(\mathbb {C}^{\Lambda _i},\|\cdot \|_i)\to (\mathbb {C}^{\Lambda ^i},\|\cdot \|^i).$
We start by supposing that there exist
![]() $\rho>0$
,
$\rho>0$
,
![]() $|\xi |\in [1,\Delta _0\rho ^{-1}]$
,
$|\xi |\in [1,\Delta _0\rho ^{-1}]$
,
![]() $i\in A$
such that
$i\in A$
such that
From this, we will derive a series of inequalities depending on parameters
![]() $\eta _0$
,
$\eta _0$
,
![]() $\eta _1$
,
$\eta _1$
,
![]() $\eta _2, \ldots,$
each new parameter
$\eta _2, \ldots,$
each new parameter
![]() $\eta _{j+1}$
will depend on
$\eta _{j+1}$
will depend on
![]() $\eta _{j}$
, not on
$\eta _{j}$
, not on
![]() $\rho $
, and
$\rho $
, and
![]() $\lim _{\eta _j\to 0}\eta _{j+1}=0$
. Finally, we will see that with the appropriate value of
$\lim _{\eta _j\to 0}\eta _{j+1}=0$
. Finally, we will see that with the appropriate value of
![]() $\Delta _0$
, the last
$\Delta _0$
, the last
![]() $\eta _j$
will be bounded away from zero and then also
$\eta _j$
will be bounded away from zero and then also
![]() $\eta _0$
, and this will complete the proof.
$\eta _0$
, and this will complete the proof.
By our assumption, there is
![]() $z=(z_{\unicode{x3bb} })\in \mathbb {C}^{\Lambda _i}$
such that
$z=(z_{\unicode{x3bb} })\in \mathbb {C}^{\Lambda _i}$
such that
![]() $\sum _{\unicode{x3bb} \in \Lambda _i}p^{\unicode{x3bb} }|z_\unicode{x3bb} |^2=1$
and for
$\sum _{\unicode{x3bb} \in \Lambda _i}p^{\unicode{x3bb} }|z_\unicode{x3bb} |^2=1$
and for
![]() $w=T_{\xi }(z)$
, we have
$w=T_{\xi }(z)$
, we have
![]() $\|w\|^2=\sum _{\unicode{x3bb} \in \Lambda ^i}p^{\unicode{x3bb} }|w_{\unicode{x3bb} }|^2\geq 1-\eta _0.$
Note that
$\|w\|^2=\sum _{\unicode{x3bb} \in \Lambda ^i}p^{\unicode{x3bb} }|w_{\unicode{x3bb} }|^2\geq 1-\eta _0.$
Note that
 $$ \begin{align*}|w_{\unicode{x3bb}}|^2=\bigg| \sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}\xi(a_{\unicode{x3bb}}^{\unicode{x3bb}'})z_{\unicode{x3bb}'}\bigg|^2\leq \bigg( \frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|\bigg)^2\leq \frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|^2.\end{align*} $$
$$ \begin{align*}|w_{\unicode{x3bb}}|^2=\bigg| \sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}\xi(a_{\unicode{x3bb}}^{\unicode{x3bb}'})z_{\unicode{x3bb}'}\bigg|^2\leq \bigg( \frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|\bigg)^2\leq \frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|^2.\end{align*} $$
Consider the set
 $$ \begin{align*}\tilde{\Lambda}=\bigg\{\unicode{x3bb} \in \Lambda^i: |w_{\unicode{x3bb}}|^2 \geq (1-\eta_1)\frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|^2\bigg\},\end{align*} $$
$$ \begin{align*}\tilde{\Lambda}=\bigg\{\unicode{x3bb} \in \Lambda^i: |w_{\unicode{x3bb}}|^2 \geq (1-\eta_1)\frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|^2\bigg\},\end{align*} $$
where
![]() $\eta _1=\eta _0^{1/2}$
. Hence,
$\eta _1=\eta _0^{1/2}$
. Hence,
 $$ \begin{align*} 1-\eta_0&\leq \sum_{\unicode{x3bb}\in \Lambda^i}p^{\unicode{x3bb}}|w_{\unicode{x3bb}}|^2= \sum_{\unicode{x3bb}\in \tilde{\Lambda}}p^{\unicode{x3bb}}|w_{\unicode{x3bb}}|^2+ \sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}p^{\unicode{x3bb}}|w_{\unicode{x3bb}}|^2\\ &<\sum_{\unicode{x3bb}\in \tilde{\Lambda}}p^{\unicode{x3bb}}\bigg(\sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\bigg)+ \sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}p^{\unicode{x3bb}}\bigg((1-\eta_1)\sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\bigg)\\ &=\sum_{\unicode{x3bb},\unicode{x3bb}'\in \Lambda} p^{\unicode{x3bb}}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2-\eta_1\sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}p^{\unicode{x3bb}}\bigg(\sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\bigg). \end{align*} $$
$$ \begin{align*} 1-\eta_0&\leq \sum_{\unicode{x3bb}\in \Lambda^i}p^{\unicode{x3bb}}|w_{\unicode{x3bb}}|^2= \sum_{\unicode{x3bb}\in \tilde{\Lambda}}p^{\unicode{x3bb}}|w_{\unicode{x3bb}}|^2+ \sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}p^{\unicode{x3bb}}|w_{\unicode{x3bb}}|^2\\ &<\sum_{\unicode{x3bb}\in \tilde{\Lambda}}p^{\unicode{x3bb}}\bigg(\sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\bigg)+ \sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}p^{\unicode{x3bb}}\bigg((1-\eta_1)\sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\bigg)\\ &=\sum_{\unicode{x3bb},\unicode{x3bb}'\in \Lambda} p^{\unicode{x3bb}}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2-\eta_1\sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}p^{\unicode{x3bb}}\bigg(\sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\bigg). \end{align*} $$
Since
![]() $\sum _{\unicode{x3bb} ,\unicode{x3bb} '\in \Lambda } p^{\unicode{x3bb} }p_{\unicode{x3bb} }^{\unicode{x3bb} '}|z_{\unicode{x3bb} '}|^2=\sum _{\unicode{x3bb} '\in \Lambda }p^{\unicode{x3bb} '}|z_{\unicode{x3bb} '}|^2=1$
and
$\sum _{\unicode{x3bb} ,\unicode{x3bb} '\in \Lambda } p^{\unicode{x3bb} }p_{\unicode{x3bb} }^{\unicode{x3bb} '}|z_{\unicode{x3bb} '}|^2=\sum _{\unicode{x3bb} '\in \Lambda }p^{\unicode{x3bb} '}|z_{\unicode{x3bb} '}|^2=1$
and
![]() $\eta _1^2=\eta _0$
, we get
$\eta _1^2=\eta _0$
, we get
 $$ \begin{align*} \eta_1&>\sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}p^{\unicode{x3bb}}\bigg(\sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\bigg) = \sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}\frac{p^{\unicode{x3bb}}}{p^i}\sum_{\unicode{x3bb}'\in \Lambda}p^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\\ &=\sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}\frac{p^{\unicode{x3bb}}}{p^i} \geq C_2\rho^{d_1+\cdots+d_n} \#(\Lambda^i\setminus \tilde{\Lambda}). \end{align*} $$
$$ \begin{align*} \eta_1&>\sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}p^{\unicode{x3bb}}\bigg(\sum_{\unicode{x3bb}'\in \Lambda}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\bigg) = \sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}\frac{p^{\unicode{x3bb}}}{p^i}\sum_{\unicode{x3bb}'\in \Lambda}p^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2\\ &=\sum_{\unicode{x3bb}\in \Lambda^i\setminus \tilde{\Lambda}}\frac{p^{\unicode{x3bb}}}{p^i} \geq C_2\rho^{d_1+\cdots+d_n} \#(\Lambda^i\setminus \tilde{\Lambda}). \end{align*} $$
Putting
![]() $\eta _2=\eta _1/C_2$
, we obtain
$\eta _2=\eta _1/C_2$
, we obtain
![]() $\#(\Lambda ^i\setminus \tilde {\Lambda })\leq \eta _2 \rho ^{-(d_1+\cdots +d_n)}.$
Proceeding as in [Reference Moreira and Yoccoz7], define
$\#(\Lambda ^i\setminus \tilde {\Lambda })\leq \eta _2 \rho ^{-(d_1+\cdots +d_n)}.$
Proceeding as in [Reference Moreira and Yoccoz7], define
![]() $Z_{\unicode{x3bb} }^{\unicode{x3bb} '}=\xi (a_{\unicode{x3bb} }^{\unicode{x3bb} '})z_{\unicode{x3bb} '}$
, then
$Z_{\unicode{x3bb} }^{\unicode{x3bb} '}=\xi (a_{\unicode{x3bb} }^{\unicode{x3bb} '})z_{\unicode{x3bb} '}$
, then
 $$ \begin{align*}\frac{1}{2}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}\sum_{\unicode{x3bb}^{\prime}_1\in \Lambda_i}p_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}p_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_1}|Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_1}|^2=\sum_{\unicode{x3bb}'\in \Lambda_i}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2-|w_{\unicode{x3bb}}|^2.\end{align*} $$
$$ \begin{align*}\frac{1}{2}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}\sum_{\unicode{x3bb}^{\prime}_1\in \Lambda_i}p_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}p_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_1}|Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_1}|^2=\sum_{\unicode{x3bb}'\in \Lambda_i}p_{\unicode{x3bb}}^{\unicode{x3bb}'}|z_{\unicode{x3bb}'}|^2-|w_{\unicode{x3bb}}|^2.\end{align*} $$
If
![]() $\unicode{x3bb} \in \tilde {\Lambda }$
,
$\unicode{x3bb} \in \tilde {\Lambda }$
,
 $$ \begin{align*}\frac{1}{2}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}\sum_{\unicode{x3bb}^{\prime}_1\in \Lambda_i}p_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}p_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_1}|Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_1}|^2\leq \frac{\eta_1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|^2=\frac{\eta_1}{p^i},\end{align*} $$
$$ \begin{align*}\frac{1}{2}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}\sum_{\unicode{x3bb}^{\prime}_1\in \Lambda_i}p_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}p_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_1}|Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_1}|^2\leq \frac{\eta_1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|^2=\frac{\eta_1}{p^i},\end{align*} $$
and hence
![]() $\sum _{\unicode{x3bb} ^{\prime }_0\in \Lambda _i}\sum _{\unicode{x3bb} ^{\prime }_1\in \Lambda _i}|Z_{\unicode{x3bb} }^{\unicode{x3bb} ^{\prime }_0}-Z_{\unicode{x3bb} }^{\unicode{x3bb} ^{\prime }_1}|^2\leq ({2(\#\Lambda _i)^2}/{p^i})\eta _1.$
Now set
$\sum _{\unicode{x3bb} ^{\prime }_0\in \Lambda _i}\sum _{\unicode{x3bb} ^{\prime }_1\in \Lambda _i}|Z_{\unicode{x3bb} }^{\unicode{x3bb} ^{\prime }_0}-Z_{\unicode{x3bb} }^{\unicode{x3bb} ^{\prime }_1}|^2\leq ({2(\#\Lambda _i)^2}/{p^i})\eta _1.$
Now set
![]() $\tilde {Z}_{\unicode{x3bb} }^{\unicode{x3bb} '}=z_{\unicode{x3bb} '}-\xi (-a_{\unicode{x3bb} }^{\unicode{x3bb} '})w_{\unicode{x3bb} }$
, then
$\tilde {Z}_{\unicode{x3bb} }^{\unicode{x3bb} '}=z_{\unicode{x3bb} '}-\xi (-a_{\unicode{x3bb} }^{\unicode{x3bb} '})w_{\unicode{x3bb} }$
, then
 $$ \begin{align*} |\tilde{Z}_{\unicode{x3bb}}^{\unicode{x3bb}'}|^2&=|\xi(a_{\unicode{x3bb}}^{\unicode{x3bb}'})z_{\unicode{x3bb}'}-w_{\unicode{x3bb}}|^2=\bigg|\xi(a_{\unicode{x3bb}}^{\unicode{x3bb}'})z_{\unicode{x3bb}'}-\frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}\bigg|^2\\ &=\bigg|\frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}(Z_{\unicode{x3bb}}^{\unicode{x3bb}'}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0})\bigg|^2\leq \frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}|Z_{\unicode{x3bb}}^{\unicode{x3bb}'}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}|^2. \end{align*} $$
$$ \begin{align*} |\tilde{Z}_{\unicode{x3bb}}^{\unicode{x3bb}'}|^2&=|\xi(a_{\unicode{x3bb}}^{\unicode{x3bb}'})z_{\unicode{x3bb}'}-w_{\unicode{x3bb}}|^2=\bigg|\xi(a_{\unicode{x3bb}}^{\unicode{x3bb}'})z_{\unicode{x3bb}'}-\frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}\bigg|^2\\ &=\bigg|\frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}(Z_{\unicode{x3bb}}^{\unicode{x3bb}'}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0})\bigg|^2\leq \frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}|Z_{\unicode{x3bb}}^{\unicode{x3bb}'}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}|^2. \end{align*} $$
Summing over
![]() $\unicode{x3bb} '$
gives
$\unicode{x3bb} '$
gives
 $$ \begin{align*}\sum_{\unicode{x3bb}'\in \Lambda_i}|\tilde{Z}_{\unicode{x3bb}}^{\unicode{x3bb}'}|^2\leq \frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}|Z_{\unicode{x3bb}}^{\unicode{x3bb}'}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}|^2\leq \frac{2\#\Lambda_i}{p^i}\eta_1\leq \eta_3 \rho^{-(d_1+\cdots+d_n)},\end{align*} $$
$$ \begin{align*}\sum_{\unicode{x3bb}'\in \Lambda_i}|\tilde{Z}_{\unicode{x3bb}}^{\unicode{x3bb}'}|^2\leq \frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}\sum_{\unicode{x3bb}^{\prime}_0\in \Lambda_i}|Z_{\unicode{x3bb}}^{\unicode{x3bb}'}-Z_{\unicode{x3bb}}^{\unicode{x3bb}^{\prime}_0}|^2\leq \frac{2\#\Lambda_i}{p^i}\eta_1\leq \eta_3 \rho^{-(d_1+\cdots+d_n)},\end{align*} $$
for
![]() $\eta _3$
a constant multiple of
$\eta _3$
a constant multiple of
![]() $\eta _1$
. Pick
$\eta _1$
. Pick
![]() $\unicode{x3bb} _0,\unicode{x3bb} _1\in \tilde {\Lambda }$
, then
$\unicode{x3bb} _0,\unicode{x3bb} _1\in \tilde {\Lambda }$
, then
![]() $z_{\unicode{x3bb} '}=\xi (-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '})w_{\unicode{x3bb} _0}+\tilde {Z}_{\unicode{x3bb} _0}^{\unicode{x3bb} '}=\xi (-a_{\unicode{x3bb} _1}^{\unicode{x3bb} '})w_{\unicode{x3bb} _1}+\tilde {Z}_{\unicode{x3bb} _1}^{\unicode{x3bb} '},$
and from this (redefine
$z_{\unicode{x3bb} '}=\xi (-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '})w_{\unicode{x3bb} _0}+\tilde {Z}_{\unicode{x3bb} _0}^{\unicode{x3bb} '}=\xi (-a_{\unicode{x3bb} _1}^{\unicode{x3bb} '})w_{\unicode{x3bb} _1}+\tilde {Z}_{\unicode{x3bb} _1}^{\unicode{x3bb} '},$
and from this (redefine
![]() $\eta _3$
as
$\eta _3$
as
![]() $4\eta _3$
),
$4\eta _3$
),

Observe that

where
![]() $\langle \xi , (t,v)\rangle =\sum _{j=1}^{n-1}\mu _j t_j+\sum _{j=1}^{n}m_j v_j\in \mathbb {T}$
for
$\langle \xi , (t,v)\rangle =\sum _{j=1}^{n-1}\mu _j t_j+\sum _{j=1}^{n}m_j v_j\in \mathbb {T}$
for
![]() $\xi =(\mu ,m)\in \mathbb {R}^{n-1}\times \mathbb {Z}^n$
, and
$\xi =(\mu ,m)\in \mathbb {R}^{n-1}\times \mathbb {Z}^n$
, and
![]() $\phi $
is the argument of the complex number
$\phi $
is the argument of the complex number
![]() $w_{\unicode{x3bb} _0}/w_{\unicode{x3bb} _1}$
. Using this inequality together with (here we assume
$w_{\unicode{x3bb} _0}/w_{\unicode{x3bb} _1}$
. Using this inequality together with (here we assume
![]() $\eta _1<3/4$
, which can be assumed without loss of generality)
$\eta _1<3/4$
, which can be assumed without loss of generality)
 $$ \begin{align*} |w_{\unicode{x3bb}}|^2 \geq (1-\eta_1)\frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|^2 = \frac{1-\eta_1}{p^i} \geq \frac{1}{4}\quad\text{for all } \unicode{x3bb}\in \tilde{\Lambda},\end{align*} $$
$$ \begin{align*} |w_{\unicode{x3bb}}|^2 \geq (1-\eta_1)\frac{1}{\#\Lambda_i}\sum_{\unicode{x3bb}'\in \Lambda_i}|z_{\unicode{x3bb}'}|^2 = \frac{1-\eta_1}{p^i} \geq \frac{1}{4}\quad\text{for all } \unicode{x3bb}\in \tilde{\Lambda},\end{align*} $$
we see that

Let
![]() $\eta _4=\eta _3^{1/3}$
. The previous inequality implies that
$\eta _4=\eta _3^{1/3}$
. The previous inequality implies that

for all
![]() $\unicode{x3bb} '\in \Lambda _i$
, but
$\unicode{x3bb} '\in \Lambda _i$
, but
![]() $\eta _4\rho ^{-(d_1+\cdots +d_n)}\ \unicode{x3bb} '$
. From this, we get
$\eta _4\rho ^{-(d_1+\cdots +d_n)}\ \unicode{x3bb} '$
. From this, we get
![]() $\|\langle \xi ,a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}\rangle +\phi \|\leq \eta _5$
for all
$\|\langle \xi ,a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}\rangle +\phi \|\leq \eta _5$
for all
![]() $\unicode{x3bb} '\in \Lambda _i$
, but
$\unicode{x3bb} '\in \Lambda _i$
, but
![]() $\eta _5\rho ^{-(d_1+\cdots +d_n)}\ \unicode{x3bb} '$
, where
$\eta _5\rho ^{-(d_1+\cdots +d_n)}\ \unicode{x3bb} '$
, where
![]() $\eta _5$
is a constant multiple of
$\eta _5$
is a constant multiple of
![]() $\eta _4$
.
$\eta _4$
.
Let
![]() $j_0$
such that
$j_0$
such that
![]() $|\xi |=|\mu _{j_0}|$
or
$|\xi |=|\mu _{j_0}|$
or
![]() $|\xi |=|m_{j_0}|$
. We will fix some specific
$|\xi |=|m_{j_0}|$
. We will fix some specific
![]() $\unicode{x3bb} _0, \unicode{x3bb} _1 \in \tilde {\Lambda }$
of the form
$\unicode{x3bb} _0, \unicode{x3bb} _1 \in \tilde {\Lambda }$
of the form

Notice that
![]() $\unicode{x3bb} _0, \unicode{x3bb} _1$
only differ on the
$\unicode{x3bb} _0, \unicode{x3bb} _1$
only differ on the
![]() $j_0$
coordinate. Moreover, if
$j_0$
coordinate. Moreover, if
![]() $j_0\neq n$
, we have
$j_0\neq n$
, we have
![]() $ a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}= (0,\ldots ,0,\log ({r_{\underline {b}^{j_0}}^{\underline {\theta }^1}}/{r_{\underline {b}^{j_0}}^{\underline {\theta }^0}}),0,\ldots ,0,v_{\underline {b}^{j_0}}^{\underline {\theta }^1}-v_{\underline {b}^{j_0}}^{\underline {\theta }^0},0,\ldots ,0) $
, where
$ a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}= (0,\ldots ,0,\log ({r_{\underline {b}^{j_0}}^{\underline {\theta }^1}}/{r_{\underline {b}^{j_0}}^{\underline {\theta }^0}}),0,\ldots ,0,v_{\underline {b}^{j_0}}^{\underline {\theta }^1}-v_{\underline {b}^{j_0}}^{\underline {\theta }^0},0,\ldots ,0) $
, where
![]() $\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^n)$
, and
$\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^n)$
, and
![]() $\underline {\theta }^0,\, \underline {\theta }^1 \in \Sigma _{j_0}^-$
end with
$\underline {\theta }^0,\, \underline {\theta }^1 \in \Sigma _{j_0}^-$
end with
![]() $\underline {a}^0$
,
$\underline {a}^0$
,
![]() $\underline {a}^1$
, respectively. If
$\underline {a}^1$
, respectively. If
![]() $j_0=n$
, then
$j_0=n$
, then
![]() $ a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}= (\log ({r^{\underline {\theta }^0}_{\underline {b}^n}}/{r^{\underline {\theta }^1}_{\underline {b}^n}}), \ldots ,\log ({r^{\underline {\theta }^0}_{\underline {b}^n}}/{r^{\underline {\theta }^1}_{\underline {b}^n}}),0,\ldots ,0,v_{\underline {b}^{n}}^{\underline {\theta }^1}-v_{\underline {b}^{n}}^{\underline {\theta }^0}). $
We remark that
$ a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}= (\log ({r^{\underline {\theta }^0}_{\underline {b}^n}}/{r^{\underline {\theta }^1}_{\underline {b}^n}}), \ldots ,\log ({r^{\underline {\theta }^0}_{\underline {b}^n}}/{r^{\underline {\theta }^1}_{\underline {b}^n}}),0,\ldots ,0,v_{\underline {b}^{n}}^{\underline {\theta }^1}-v_{\underline {b}^{n}}^{\underline {\theta }^0}). $
We remark that
![]() $a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}$
only depends on the
$a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}$
only depends on the
![]() $j_0$
Cantor set
$j_0$
Cantor set
![]() $K_{j_0}$
.
$K_{j_0}$
.
Given that
![]() $K_{j_0}$
is not essentially affine, there is
$K_{j_0}$
is not essentially affine, there is
![]() $\tilde {\underline {\theta }}^0, \tilde {\underline {\theta }}^1 \in \Sigma _{j_0}^-$
and
$\tilde {\underline {\theta }}^0, \tilde {\underline {\theta }}^1 \in \Sigma _{j_0}^-$
and
![]() $x_0\in K_{j_0}^{\tilde {\underline {\theta }}^0}$
such that
$x_0\in K_{j_0}^{\tilde {\underline {\theta }}^0}$
such that
For any
![]() $\underline {\theta }^0, \underline {\theta }^1 \in \Sigma _{j_0}^-$
, we define
$\underline {\theta }^0, \underline {\theta }^1 \in \Sigma _{j_0}^-$
, we define
![]() $F_{\underline {\theta }^0,\underline {\theta }^1}:=k^{\underline {\theta }^1}\circ (k^{\underline {\theta }^0})^{-1}$
. Since
$F_{\underline {\theta }^0,\underline {\theta }^1}:=k^{\underline {\theta }^1}\circ (k^{\underline {\theta }^0})^{-1}$
. Since
![]() $x_0\in K_{j_0}^{\tilde {\underline {\theta }}^0}$
, then
$x_0\in K_{j_0}^{\tilde {\underline {\theta }}^0}$
, then
![]() $DF_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)$
is a conformal matrix. Denote by
$DF_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)$
is a conformal matrix. Denote by
![]() $C\subset GL(2,\mathbb {R})$
the set of
$C\subset GL(2,\mathbb {R})$
the set of
![]() $2\times 2$
conformal matrices. Let
$2\times 2$
conformal matrices. Let
![]() $P:U\to C$
be a smooth function from a neighborhood
$P:U\to C$
be a smooth function from a neighborhood
![]() $U\subset GL(2,\mathbb {R})$
of
$U\subset GL(2,\mathbb {R})$
of
![]() $DF_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)$
into C, such that
$DF_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)$
into C, such that
![]() $P(A)=A$
for all
$P(A)=A$
for all
![]() $A\in C\cap U$
. We will use the notation
$A\in C\cap U$
. We will use the notation
![]() $\mathbb {D}F_{\underline {\theta }^0,\underline {\theta }^1}(x)= P(DF_{\underline {\theta }^0,\underline {\theta }^1}(x))$
. The properties of P and the fact that
$\mathbb {D}F_{\underline {\theta }^0,\underline {\theta }^1}(x)= P(DF_{\underline {\theta }^0,\underline {\theta }^1}(x))$
. The properties of P and the fact that
![]() $K_{j_0}$
is not essentially real allow us to conclude that
$K_{j_0}$
is not essentially real allow us to conclude that
![]() $D\mathbb {D}F_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)= D^2 F_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)$
. Now notice that C can be naturally identified with
$D\mathbb {D}F_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)= D^2 F_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)$
. Now notice that C can be naturally identified with
![]() $\mathbb {C}^*$
and in this sense, we can choose a branch of logarithm
$\mathbb {C}^*$
and in this sense, we can choose a branch of logarithm
![]() $\log $
defined in
$\log $
defined in
![]() $P(U)$
(for U small). Then Lemma 2.3 will imply that
$P(U)$
(for U small). Then Lemma 2.3 will imply that
![]() $\beta := D \log \mathbb {D}F_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)\neq 0$
is a conformal matrix.
$\beta := D \log \mathbb {D}F_{\tilde {\underline {\theta }}^0,\tilde {\underline {\theta }}^1}(x_0)\neq 0$
is a conformal matrix.
In the rest of the proof, we will make an abuse of notation, where
![]() $v_{\underline {b}^{j_0}}^{\underline {\theta }^1}-v_{\underline {b}^{j_0}}^{\underline {\theta }^0}$
will not represent an element of
$v_{\underline {b}^{j_0}}^{\underline {\theta }^1}-v_{\underline {b}^{j_0}}^{\underline {\theta }^0}$
will not represent an element of
![]() $\mathbb {T}$
but the imaginary part of
$\mathbb {T}$
but the imaginary part of
![]() $\log \exp [(v_{\underline {b}^{j_0}}^{\underline {\theta }^1}-v_{\underline {b}^{j_0}}^{\underline {\theta }^0})i]$
. In this way, we have chosen a representative in the class defined by
$\log \exp [(v_{\underline {b}^{j_0}}^{\underline {\theta }^1}-v_{\underline {b}^{j_0}}^{\underline {\theta }^0})i]$
. In this way, we have chosen a representative in the class defined by
![]() $v_{\underline {b}^{j_0}}^{\underline {\theta }^1}-v_{\underline {b}^{j_0}}^{\underline {\theta }^0}$
. Define the following vectors in
$v_{\underline {b}^{j_0}}^{\underline {\theta }^1}-v_{\underline {b}^{j_0}}^{\underline {\theta }^0}$
. Define the following vectors in
![]() $\mathbb {R}^2$
:
$\mathbb {R}^2$
:

and
 $$ \begin{align*} \tilde{\xi}= \begin{cases} (\mu_{j_0},m_{j_0}) & \mbox{if } j_0\neq n, \\ (-(\mu_1+\cdots+\mu_{n-1}),m_n) & \mbox{if } j_0=n. \end{cases} \end{align*} $$
$$ \begin{align*} \tilde{\xi}= \begin{cases} (\mu_{j_0},m_{j_0}) & \mbox{if } j_0\neq n, \\ (-(\mu_1+\cdots+\mu_{n-1}),m_n) & \mbox{if } j_0=n. \end{cases} \end{align*} $$
Notice that
![]() $1\leq |\tilde {\xi }|\leq n \Delta _0 \rho ^{-1}$
and
$1\leq |\tilde {\xi }|\leq n \Delta _0 \rho ^{-1}$
and
![]() $\langle \xi ,a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}\rangle =\langle \tilde {\xi }, d_{\unicode{x3bb} _1, \unicode{x3bb} _0}^{\unicode{x3bb} '}\rangle \mod 2\pi \mathbb {Z},$
where the
$\langle \xi ,a_{\unicode{x3bb} _1}^{\unicode{x3bb} '}-a_{\unicode{x3bb} _0}^{\unicode{x3bb} '}\rangle =\langle \tilde {\xi }, d_{\unicode{x3bb} _1, \unicode{x3bb} _0}^{\unicode{x3bb} '}\rangle \mod 2\pi \mathbb {Z},$
where the
![]() $\langle \cdot , \cdot \rangle $
in the right-hand side of the equation refers to the usual inner product on
$\langle \cdot , \cdot \rangle $
in the right-hand side of the equation refers to the usual inner product on
![]() $\mathbb {R}^2$
.
$\mathbb {R}^2$
.
Since
![]() $k^{\underline {\theta }}$
depends continuously on
$k^{\underline {\theta }}$
depends continuously on
![]() $\underline {\theta }$
, we get that
$\underline {\theta }$
, we get that
for all
![]() $\underline {\theta }^0$
,
$\underline {\theta }^0$
,
![]() $\underline {\theta }^1$
, x close enough to
$\underline {\theta }^1$
, x close enough to
![]() $\tilde {\underline {\theta }}^0$
,
$\tilde {\underline {\theta }}^0$
,
![]() $\tilde {\underline {\theta }}^1$
,
$\tilde {\underline {\theta }}^1$
,
![]() $x_0$
; the value of
$x_0$
; the value of
![]() $\delta _1$
will be fixed later. We assume that
$\delta _1$
will be fixed later. We assume that
![]() $\eta _2$
is small such that the proportion of
$\eta _2$
is small such that the proportion of
![]() $\tilde {\Lambda }$
inside
$\tilde {\Lambda }$
inside
![]() $\Lambda ^i$
is big enough to exist
$\Lambda ^i$
is big enough to exist
![]() $\unicode{x3bb} _0, \unicode{x3bb} _1\in \tilde {\Lambda }$
, with the form specified before, verifying that
$\unicode{x3bb} _0, \unicode{x3bb} _1\in \tilde {\Lambda }$
, with the form specified before, verifying that
![]() $\underline {\theta }^0$
,
$\underline {\theta }^0$
,
![]() $\underline {\theta }^1$
are close to
$\underline {\theta }^1$
are close to
![]() $\tilde {\underline {\theta }^0}$
,
$\tilde {\underline {\theta }^0}$
,
![]() $\tilde {\underline {\theta }^1}$
so that equation (20) holds. (Here we also need to suppose that
$\tilde {\underline {\theta }^1}$
so that equation (20) holds. (Here we also need to suppose that
![]() $\rho _0$
is small enough.) From now on,
$\rho _0$
is small enough.) From now on,
![]() $\unicode{x3bb} _0$
and
$\unicode{x3bb} _0$
and
![]() $\unicode{x3bb} _1$
are fixed as these values.
$\unicode{x3bb} _1$
are fixed as these values.
Now fix
![]() $\underline {c}^0\in \Sigma _{j_0}^\textit{fin}$
such that any x in the convex hull of
$\underline {c}^0\in \Sigma _{j_0}^\textit{fin}$
such that any x in the convex hull of
![]() $G^{\underline {\theta }^0}(\underline {c}^0)$
is close enough to
$G^{\underline {\theta }^0}(\underline {c}^0)$
is close enough to
![]() $x_0$
to have equation (20). Denote by
$x_0$
to have equation (20). Denote by
![]() $\Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
all the elements of
$\Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
all the elements of
![]() $\Sigma _{j_0}(\tilde {c}_0,\rho )$
starting with
$\Sigma _{j_0}(\tilde {c}_0,\rho )$
starting with
![]() $\underline {c}^0$
. This is a positive proportion of
$\underline {c}^0$
. This is a positive proportion of
![]() $\Sigma _{j_0}(\tilde {c}_0,\rho )$
(independent of
$\Sigma _{j_0}(\tilde {c}_0,\rho )$
(independent of
![]() $\rho $
). Then, if we assume
$\rho $
). Then, if we assume
![]() $\eta _5$
small enough, we can guarantee that for a proportion of
$\eta _5$
small enough, we can guarantee that for a proportion of
![]() $\underline {b}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
, as big as we want, there exist
$\underline {b}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
, as big as we want, there exist
![]() $\underline {b}^j\in \Sigma _j(\tilde {c}_0,\rho )$
,
$\underline {b}^j\in \Sigma _j(\tilde {c}_0,\rho )$
,
![]() $j\neq j_0$
, such that
$j\neq j_0$
, such that
![]() $\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^{j_0-1},\underline {b},\underline {b}^{j_0+1},\ldots ,\underline {b}^n)$
verifies
$\unicode{x3bb} '=(\underline {b}^1,\ldots ,\underline {b}^{j_0-1},\underline {b},\underline {b}^{j_0+1},\ldots ,\underline {b}^n)$
verifies
where
![]() $m(\underline {b})$
is an integer depending on
$m(\underline {b})$
is an integer depending on
![]() $\underline {b}$
. Denote the set of such
$\underline {b}$
. Denote the set of such
![]() $\underline {b}$
by
$\underline {b}$
by
![]() $\tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
.
$\tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
.
For simplicity, write
![]() $F=k^{\underline {\theta }^1}\circ (k^{\underline {\theta }^0})^{-1}$
, instead of
$F=k^{\underline {\theta }^1}\circ (k^{\underline {\theta }^0})^{-1}$
, instead of
![]() $F_{\underline {\theta }^0,\underline {\theta }^1}$
, then we have
$F_{\underline {\theta }^0,\underline {\theta }^1}$
, then we have
We will show that the distance between
![]() $\log \mathbb {D}F(c_{\underline {b}}^{\underline {\theta }^0})$
and
$\log \mathbb {D}F(c_{\underline {b}}^{\underline {\theta }^0})$
and
![]() $d_{\unicode{x3bb} _1,\unicode{x3bb} _0}^{\unicode{x3bb} '}$
is of order
$d_{\unicode{x3bb} _1,\unicode{x3bb} _0}^{\unicode{x3bb} '}$
is of order
![]() $\rho $
for any
$\rho $
for any
![]() $\unicode{x3bb} '\in \Lambda $
. Let
$\unicode{x3bb} '\in \Lambda $
. Let
![]() $z_0, z_1 \in G^{\underline {\theta }^0}(\underline {b})$
such that
$z_0, z_1 \in G^{\underline {\theta }^0}(\underline {b})$
such that
![]() $r^{\underline {\theta }^0}_{\underline {b}}=|z_0-z_1|$
. Using Taylor expansion at
$r^{\underline {\theta }^0}_{\underline {b}}=|z_0-z_1|$
. Using Taylor expansion at
![]() $c^{\underline {\theta }^0}_{\underline {b}}$
, we get
$c^{\underline {\theta }^0}_{\underline {b}}$
, we get
![]() $F(z_0)-F(z_1)=DF(c^{\underline {\theta }^0}_{\underline {b}})(z_0-z_1)+O(|z_0-z_1|^2),$
where the constant in the O notation does not depend on
$F(z_0)-F(z_1)=DF(c^{\underline {\theta }^0}_{\underline {b}})(z_0-z_1)+O(|z_0-z_1|^2),$
where the constant in the O notation does not depend on
![]() $\rho $
,
$\rho $
,
![]() $\underline {b}$
,
$\underline {b}$
,
![]() $\underline {\theta }^1$
, or
$\underline {\theta }^1$
, or
![]() $\underline {\theta }^0$
. Hence,
$\underline {\theta }^0$
. Hence,
 $$ \begin{align*} r_{\underline{b}}^{\underline{\theta}^0}\|DF(c_{\underline{b}}^{\underline{\theta}^0})\|&=|z_0-z_1|\|DF(c_{\underline{b}}^{\underline{\theta}^0})\|\\ &\leq |F(z_0)-F(z_1)|+O(|z_0-z_1|^2) \leq r_{\underline{b}}^{\underline{\theta}^1}+O((r_{\underline{b}}^{\underline{\theta}^0})^2). \end{align*} $$
$$ \begin{align*} r_{\underline{b}}^{\underline{\theta}^0}\|DF(c_{\underline{b}}^{\underline{\theta}^0})\|&=|z_0-z_1|\|DF(c_{\underline{b}}^{\underline{\theta}^0})\|\\ &\leq |F(z_0)-F(z_1)|+O(|z_0-z_1|^2) \leq r_{\underline{b}}^{\underline{\theta}^1}+O((r_{\underline{b}}^{\underline{\theta}^0})^2). \end{align*} $$
From this and the fact that
![]() $r_{\underline {b}}^{\underline {\theta }^0}$
is of order
$r_{\underline {b}}^{\underline {\theta }^0}$
is of order
![]() $\rho $
, we get
$\rho $
, we get
![]() $ \|DF(c_{\underline {b}}^{\underline {\theta }^0})\|-{r_{\underline {b}}^{\underline {\theta }^1}}/{r_{\underline {b}}^{\underline {\theta }^0}} \leq O(\rho ).$
A similar argument gives
$ \|DF(c_{\underline {b}}^{\underline {\theta }^0})\|-{r_{\underline {b}}^{\underline {\theta }^1}}/{r_{\underline {b}}^{\underline {\theta }^0}} \leq O(\rho ).$
A similar argument gives
![]() ${r_{\underline {b}}^{\underline {\theta }^1}}/{r_{\underline {b}}^{\underline {\theta }^0}}-\|DF(c_{\underline {b}}^{\underline {\theta }^0})\| \leq O(\rho ).$
Therefore,
${r_{\underline {b}}^{\underline {\theta }^1}}/{r_{\underline {b}}^{\underline {\theta }^0}}-\|DF(c_{\underline {b}}^{\underline {\theta }^0})\| \leq O(\rho ).$
Therefore,
![]() $ | \|DF(c_{\underline {b}}^{\underline {\theta }^0})\|-{r_{\underline {b}}^{\underline {\theta }^1}}/{r_{\underline {b}}^{\underline {\theta }^0}} | \leq O(\rho ).$
$ | \|DF(c_{\underline {b}}^{\underline {\theta }^0})\|-{r_{\underline {b}}^{\underline {\theta }^1}}/{r_{\underline {b}}^{\underline {\theta }^0}} | \leq O(\rho ).$
Now, given the fact that
![]() $\|DF(c_{\underline {b}}^{\underline {\theta }^0})\|$
and
$\|DF(c_{\underline {b}}^{\underline {\theta }^0})\|$
and
![]() $r_{\underline {b}}^{\underline {\theta }^1}/r_{\underline {b}}^{\underline {\theta }^0}$
are uniformly bounded away from zero, we obtain that there is a constant
$r_{\underline {b}}^{\underline {\theta }^1}/r_{\underline {b}}^{\underline {\theta }^0}$
are uniformly bounded away from zero, we obtain that there is a constant
![]() $C_3>0$
, independent of
$C_3>0$
, independent of
![]() $\rho $
, such that
$\rho $
, such that
Given
![]() $\underline {b}^1,\underline {b}^2\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
, by the choice of
$\underline {b}^1,\underline {b}^2\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
, by the choice of
![]() $\underline {c}^0$
, using Taylor approximation and equation (20), we will have that
$\underline {c}^0$
, using Taylor approximation and equation (20), we will have that
for some
![]() $\beta _1$
such that
$\beta _1$
such that
![]() $\|\beta _1-\beta \|\leq \delta _1$
.
$\|\beta _1-\beta \|\leq \delta _1$
.
The idea to finish the proof is the following: we use equation (21) to see that the set of
![]() $d_{\unicode{x3bb} _1, \unicode{x3bb} _0}^{\unicode{x3bb} '}$
projected to the line generated by
$d_{\unicode{x3bb} _1, \unicode{x3bb} _0}^{\unicode{x3bb} '}$
projected to the line generated by
![]() $\tilde {\xi }$
is close to an arithmetic progression, then two points will be either very close or very far from each other. Equations (22), (23), (24) allow to translate this fact about
$\tilde {\xi }$
is close to an arithmetic progression, then two points will be either very close or very far from each other. Equations (22), (23), (24) allow to translate this fact about
![]() $d_{\unicode{x3bb} _1,\unicode{x3bb} _0}^{\unicode{x3bb} '}$
to the analogous one about the set of
$d_{\unicode{x3bb} _1,\unicode{x3bb} _0}^{\unicode{x3bb} '}$
to the analogous one about the set of
![]() $c^{\underline {\theta }^0}_{\underline {b}}$
. Finally, we will use the fact that
$c^{\underline {\theta }^0}_{\underline {b}}$
. Finally, we will use the fact that
![]() $K_{j_0}$
is not essentially real to estimate
$K_{j_0}$
is not essentially real to estimate
![]() $|c^{\underline {\theta }^0}_{\underline {b}^1}-c^{\underline {\theta }^0}_{\underline {b}^2}|$
from
$|c^{\underline {\theta }^0}_{\underline {b}^1}-c^{\underline {\theta }^0}_{\underline {b}^2}|$
from
![]() $\langle \tilde {\xi }, \beta _1 (c^{\underline {\theta }^0}_{\underline {b}^1}-c^{\underline {\theta }^0}_{\underline {b}^2})\rangle $
, and thus it will happen that
$\langle \tilde {\xi }, \beta _1 (c^{\underline {\theta }^0}_{\underline {b}^1}-c^{\underline {\theta }^0}_{\underline {b}^2})\rangle $
, and thus it will happen that
![]() $|c^{\underline {\theta }^0}_{\underline {b}^1}-c^{\underline {\theta }^0}_{\underline {b}^2}|$
is either too big or too small which will bring us into a contradiction with the boundedness of the geometry of the Cantor set.
$|c^{\underline {\theta }^0}_{\underline {b}^1}-c^{\underline {\theta }^0}_{\underline {b}^2}|$
is either too big or too small which will bring us into a contradiction with the boundedness of the geometry of the Cantor set.
Any pair
![]() $\underline {b}_1, \underline {b}_2 \in \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
should verify one of two options.
$\underline {b}_1, \underline {b}_2 \in \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
should verify one of two options.
-
(i) If
 $m(\underline {b}_1)=m(\underline {b}_2)$
, using equation (21) for
$m(\underline {b}_1)=m(\underline {b}_2)$
, using equation (21) for
 $\unicode{x3bb} ^{\prime }_1$
,
$\unicode{x3bb} ^{\prime }_1$
,
 $\unicode{x3bb} ^{\prime }_2$
associated to
$\unicode{x3bb} ^{\prime }_2$
associated to
 $\underline {b}_1$
,
$\underline {b}_1$
,
 $\underline {b}_2$
, respectively, we get
$\underline {b}_2$
, respectively, we get
 $ |\langle \tilde {\xi },d_{\unicode{x3bb} _1,\unicode{x3bb} _0}^{\unicode{x3bb} ^{\prime }_1}\rangle -\langle \tilde {\xi },d_{\unicode{x3bb} _1,\unicode{x3bb} _0}^{\unicode{x3bb} ^{\prime }_2}\rangle |\leq 2\eta _5.$
This together with equations (22), (23) give Considering equation (24) leads to
$ |\langle \tilde {\xi },d_{\unicode{x3bb} _1,\unicode{x3bb} _0}^{\unicode{x3bb} ^{\prime }_1}\rangle -\langle \tilde {\xi },d_{\unicode{x3bb} _1,\unicode{x3bb} _0}^{\unicode{x3bb} ^{\prime }_2}\rangle |\leq 2\eta _5.$
This together with equations (22), (23) give Considering equation (24) leads to $$ \begin{align*}| \langle \tilde{\xi}, \log \mathbb{D}F(c_{\underline{b}_1}^{\underline{\theta}^0})-\log \mathbb{D}F(c_{\underline{b}_2}^{\underline{\theta}^0})\rangle| \leq 2\eta_5+2C_3 |\tilde{\xi}|\rho. \end{align*} $$
where
$$ \begin{align*}| \langle \tilde{\xi}, \log \mathbb{D}F(c_{\underline{b}_1}^{\underline{\theta}^0})-\log \mathbb{D}F(c_{\underline{b}_2}^{\underline{\theta}^0})\rangle| \leq 2\eta_5+2C_3 |\tilde{\xi}|\rho. \end{align*} $$
where $$ \begin{align*} |\langle \beta_1^T \tilde{\xi},c_{\underline{b}_1}^{\underline{\theta}^0}-c_{\underline{b}_2}^{\underline{\theta}^0}\rangle|=|\langle \tilde{\xi},\beta_1(c_{\underline{b}_1}^{\underline{\theta}^0}-c_{\underline{b}_2}^{\underline{\theta}^0})\rangle | \leq 2\eta_5+2C_3 |\tilde{\xi}|\rho,\end{align*} $$
$$ \begin{align*} |\langle \beta_1^T \tilde{\xi},c_{\underline{b}_1}^{\underline{\theta}^0}-c_{\underline{b}_2}^{\underline{\theta}^0}\rangle|=|\langle \tilde{\xi},\beta_1(c_{\underline{b}_1}^{\underline{\theta}^0}-c_{\underline{b}_2}^{\underline{\theta}^0})\rangle | \leq 2\eta_5+2C_3 |\tilde{\xi}|\rho,\end{align*} $$
 $\beta _1^T$
is the transpose of
$\beta _1^T$
is the transpose of
 $\beta _1$
.
$\beta _1$
.
-
(ii) If
 $m(\underline {b}_1)\neq m(\underline {b}_2)$
, a similar process arrives to
$m(\underline {b}_1)\neq m(\underline {b}_2)$
, a similar process arrives to  $$ \begin{align*} |\langle \beta_1^T \tilde{\xi},c_{\underline{b}_1}^{\underline{\theta}^0}-c_{\underline{b}_2}^{\underline{\theta}^0}\rangle| \geq \pi-2C_3 |\tilde{\xi}|\rho.\end{align*} $$
$$ \begin{align*} |\langle \beta_1^T \tilde{\xi},c_{\underline{b}_1}^{\underline{\theta}^0}-c_{\underline{b}_2}^{\underline{\theta}^0}\rangle| \geq \pi-2C_3 |\tilde{\xi}|\rho.\end{align*} $$
Now we use the hypothesis that
![]() $K_{j_0}$
is not essentially real. First, we choose a constant
$K_{j_0}$
is not essentially real. First, we choose a constant
![]() $C_5>0$
, depending only on
$C_5>0$
, depending only on
![]() $\tilde {c}_0$
and the Cantor set
$\tilde {c}_0$
and the Cantor set
![]() $K_{j_0}$
, such that for any
$K_{j_0}$
, such that for any
![]() $\underline {a}\in \Sigma _{j_0}^\textit{fin}$
, one has
$\underline {a}\in \Sigma _{j_0}^\textit{fin}$
, one has
for some
![]() $\tilde {\rho }>0$
, which depends on
$\tilde {\rho }>0$
, which depends on
![]() $\rho $
and
$\rho $
and
![]() $\underline {a}$
. Lemma 2.2 proves that there is an angle
$\underline {a}$
. Lemma 2.2 proves that there is an angle
![]() $\alpha \in (0,\pi /2)$
and numbers
$\alpha \in (0,\pi /2)$
and numbers
![]() $\rho _2>0$
,
$\rho _2>0$
,
![]() $a\in (0,1)$
such that for any limit geometry
$a\in (0,1)$
such that for any limit geometry
![]() $k^{\underline {\theta }}$
,
$k^{\underline {\theta }}$
,
![]() $x\in G^{\underline {\theta }}(\theta _0)$
, line L,
$x\in G^{\underline {\theta }}(\theta _0)$
, line L,
![]() $s\in \mathbb {A}_{j_0}$
, D discretization of
$s\in \mathbb {A}_{j_0}$
, D discretization of
![]() $K_{j_0}(\theta _0, s)$
of order less than
$K_{j_0}(\theta _0, s)$
of order less than
![]() $\rho _2$
,
$\rho _2$
,
Remember that a discretization D of
![]() $K_{j_0}(\theta _0, s)$
of order
$K_{j_0}(\theta _0, s)$
of order
![]() $\rho $
is a subset of
$\rho $
is a subset of
![]() $\Sigma _{j_0} (C_5,\rho )$
such that
$\Sigma _{j_0} (C_5,\rho )$
such that
![]() $\bigcup _{\underline {a}\in D}K_{j_0}(\underline {a})=K_{j_0}(\theta _0, s)$
for some pre-fixed constant
$\bigcup _{\underline {a}\in D}K_{j_0}(\underline {a})=K_{j_0}(\theta _0, s)$
for some pre-fixed constant
![]() $C_5$
.
$C_5$
.
Fix
![]() $\delta _1$
by requiring that
$\delta _1$
by requiring that
![]() $\|\beta _1-\beta \|<\delta _1$
implies that
$\|\beta _1-\beta \|<\delta _1$
implies that
and the angle between
![]() $\beta ^T w$
and
$\beta ^T w$
and
![]() $\beta _1^T w$
is less than
$\beta _1^T w$
is less than
![]() $\alpha /2$
for any
$\alpha /2$
for any
![]() $w\in \mathbb {R} \setminus \{0\}$
. Remember that
$w\in \mathbb {R} \setminus \{0\}$
. Remember that ![]() and that
and that
![]() $\beta $
is conformal, and hence
$\beta $
is conformal, and hence
![]() $m(\beta ^T)=m(\beta )=\|\beta \|=\|\beta ^T\|$
. Fix
$m(\beta ^T)=m(\beta )=\|\beta \|=\|\beta ^T\|$
. Fix
![]() $\tilde {a}\in (a,1)$
. Assuming
$\tilde {a}\in (a,1)$
. Assuming
![]() $\eta _5$
small enough, we can guarantee that
$\eta _5$
small enough, we can guarantee that
This allows us to find a finite sequence
![]() $\underline {c}^0,\ldots ,\underline {c}^m$
of elements of
$\underline {c}^0,\ldots ,\underline {c}^m$
of elements of
![]() $\Sigma ^\textit{fin}$
such that:
$\Sigma ^\textit{fin}$
such that:
-
•
 $\underline {c}^{j+1}$
starts with
$\underline {c}^{j+1}$
starts with
 $\underline {c}^j$
and has one more letter;
$\underline {c}^j$
and has one more letter; -
•
 $\#(\Sigma _{j_0}(\tilde {c}_0,\rho , \underline {c}^j)\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho , \underline {c}^0))> \tilde {a}\cdot \#\Sigma _{j_0}(\tilde {c}_0,\rho , \underline {c}^j)$
;
$\#(\Sigma _{j_0}(\tilde {c}_0,\rho , \underline {c}^j)\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho , \underline {c}^0))> \tilde {a}\cdot \#\Sigma _{j_0}(\tilde {c}_0,\rho , \underline {c}^j)$
; -
•
 $\Sigma _{j_0}(\tilde {c}_0,\rho , \underline {c}^j)\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho , \underline {c}^0) \not \subset \Sigma _{j_0}(\tilde {c}_0,\rho , \underline {c}^{j+1})$
(actually, for this property to be true, we take
$\Sigma _{j_0}(\tilde {c}_0,\rho , \underline {c}^j)\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho , \underline {c}^0) \not \subset \Sigma _{j_0}(\tilde {c}_0,\rho , \underline {c}^{j+1})$
(actually, for this property to be true, we take
 $\tilde {a}$
big such that
$\tilde {a}$
big such that
 $\#\Sigma _{\tilde {c}_0}(\rho , \underline {c}^{j+1})<\tilde {a}\cdot \Sigma _{\tilde {c}_0}(\rho , \underline {c}^j)$
);
$\#\Sigma _{\tilde {c}_0}(\rho , \underline {c}^{j+1})<\tilde {a}\cdot \Sigma _{\tilde {c}_0}(\rho , \underline {c}^j)$
); -
•
 $\underline {c}^j \in \Sigma _{j_0}(\tilde {c}_0,\rho )$
only for
$\underline {c}^j \in \Sigma _{j_0}(\tilde {c}_0,\rho )$
only for
 $j=m$
.
$j=m$
.
Fix an integer
![]() $m_0<m$
such that for any
$m_0<m$
such that for any
![]() $\underline {b}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^j)$
and
$\underline {b}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^j)$
and
![]() $j<m_0$
, we have
$j<m_0$
, we have
![]() $f_{\underline {c}^j}^{-1}(G(\underline {b}))=G(\underline {b}')$
for
$f_{\underline {c}^j}^{-1}(G(\underline {b}))=G(\underline {b}')$
for
![]() $\underline {b}'\in \Sigma _{j_0}(C_5,\tilde {\rho })$
, for
$\underline {b}'\in \Sigma _{j_0}(C_5,\tilde {\rho })$
, for
![]() $\tilde {\rho }<\rho _2$
(this only requires that
$\tilde {\rho }<\rho _2$
(this only requires that
![]() $m-m_0$
is big enough). For each
$m-m_0$
is big enough). For each
![]() $\underline {c}^j$
,
$\underline {c}^j$
,
![]() $j<m$
, we will choose two elements
$j<m$
, we will choose two elements
![]() $\underline {a}^{1,j}, \underline {a}^{2,j}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^j)\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
in the following way.
$\underline {a}^{1,j}, \underline {a}^{2,j}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^j)\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
in the following way.
-
• First, we choose any
 $\underline {a}^{1,j} \in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^j s')\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
, where
$\underline {a}^{1,j} \in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^j s')\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
, where
 $s'$
is a letter in
$s'$
is a letter in
 $\mathbb {A}_{j_0}$
such that
$\mathbb {A}_{j_0}$
such that
 $\underline {c}^{j+1}\neq \underline {c}^j s'$
.
$\underline {c}^{j+1}\neq \underline {c}^j s'$
. -
• If
 $j\geq m_0$
, then we choose any
$j\geq m_0$
, then we choose any
 $\underline {a}^{2,j}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^{j+1})\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
.
$\underline {a}^{2,j}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^{j+1})\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
. -
• Suppose
 $j<m_0$
. Given
$j<m_0$
. Given
 $\underline {b}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^{j+1})$
, it can be written as where
$\underline {b}\in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^{j+1})$
, it can be written as where $$ \begin{align*}\underline{b}=(c^j_{-k},\ldots,c^j_{-1},c^j_0,c^{j+1}_0,b_1,\ldots,b_p),\end{align*} $$
$$ \begin{align*}\underline{b}=(c^j_{-k},\ldots,c^j_{-1},c^j_0,c^{j+1}_0,b_1,\ldots,b_p),\end{align*} $$
 $c^j_0$
,
$c^j_0$
,
 $c^{j+1}_0$
are the last letters of
$c^{j+1}_0$
are the last letters of
 $\underline {c}^j$
,
$\underline {c}^j$
,
 $\underline {c}^{j+1}$
, respectively. Using this notation, we can define the set This set is a discretization of
$\underline {c}^{j+1}$
, respectively. Using this notation, we can define the set This set is a discretization of $$ \begin{align*}D&=\{(c^j_0,c^{j+1}_0,b_1,\ldots,b_p)\in \Sigma^\textit{fin}: (c^j_{-k},\ldots,c^j_{-1},c^j_0,c^{j+1}_0,b_1,\ldots,b_p)\\&\in \Sigma_{j_0}(\tilde{c}_0,\rho,\underline{c}^{j+1})\}.\end{align*} $$
$$ \begin{align*}D&=\{(c^j_0,c^{j+1}_0,b_1,\ldots,b_p)\in \Sigma^\textit{fin}: (c^j_{-k},\ldots,c^j_{-1},c^j_0,c^{j+1}_0,b_1,\ldots,b_p)\\&\in \Sigma_{j_0}(\tilde{c}_0,\rho,\underline{c}^{j+1})\}.\end{align*} $$
 $K_{j_0}(c^j_0,c^{j+1}_0)$
and by our choice of
$K_{j_0}(c^j_0,c^{j+1}_0)$
and by our choice of
 $m_0$
, it has order less than
$m_0$
, it has order less than
 $\rho _2$
. Now use Lemma 2.2 for the limit geometry
$\rho _2$
. Now use Lemma 2.2 for the limit geometry
 $K_{j_0}^{\underline {\theta }^0 \underline {c}^j}$
, point
$K_{j_0}^{\underline {\theta }^0 \underline {c}^j}$
, point
 $x=(F^{\underline {\theta }^0}_{\underline {c}^j})^{-1}(c^{\underline {\theta }^0}_{\underline {a}^{1,j}})$
, and line L such that
$x=(F^{\underline {\theta }^0}_{\underline {c}^j})^{-1}(c^{\underline {\theta }^0}_{\underline {a}^{1,j}})$
, and line L such that
 $F^{\underline {\theta }^0}_{\underline {c}^j}(L)$
is orthogonal to the line generated by
$F^{\underline {\theta }^0}_{\underline {c}^j}(L)$
is orthogonal to the line generated by
 $\beta ^T \tilde {\xi }$
. Hence, and then
$\beta ^T \tilde {\xi }$
. Hence, and then $$ \begin{align*}\#\{\underline{a}\in D:\,\, G^{\underline{\theta}^0 \underline{c}^j}(\underline{a})\cap \mathrm{Cone}(x,L,\alpha)\neq \emptyset \}\leq a\cdot \#D,\end{align*} $$
Since
$$ \begin{align*}\#\{\underline{a}\in D:\,\, G^{\underline{\theta}^0 \underline{c}^j}(\underline{a})\cap \mathrm{Cone}(x,L,\alpha)\neq \emptyset \}\leq a\cdot \#D,\end{align*} $$
Since $$ \begin{align*}&\#\{\underline{b}\in \Sigma_{j_0}(\tilde{c}_0,\rho,\underline{c}^{j+1}): G^{\underline{\theta}^0}(\underline{b})\cap \mathrm{ Cone}(c^{\underline{\theta}^0}_{\underline{a}^{1,j}},F^{\underline{\theta}^0}_{\underline{c}^j}(L),\alpha)\neq \emptyset \}\\&\quad\leq a\cdot \# \Sigma_{j_0}(\tilde{c}_0,\rho,\underline{c}^{j+1}).\end{align*} $$
$$ \begin{align*}&\#\{\underline{b}\in \Sigma_{j_0}(\tilde{c}_0,\rho,\underline{c}^{j+1}): G^{\underline{\theta}^0}(\underline{b})\cap \mathrm{ Cone}(c^{\underline{\theta}^0}_{\underline{a}^{1,j}},F^{\underline{\theta}^0}_{\underline{c}^j}(L),\alpha)\neq \emptyset \}\\&\quad\leq a\cdot \# \Sigma_{j_0}(\tilde{c}_0,\rho,\underline{c}^{j+1}).\end{align*} $$
 $\tilde {a}>a$
, then there are elements
$\tilde {a}>a$
, then there are elements
 $\underline {a} \in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^{j+1})\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
such that We choose
$\underline {a} \in \Sigma _{j_0}(\tilde {c}_0,\rho ,\underline {c}^{j+1})\cap \tilde {\Sigma }_{j_0}(\tilde {c}_0,\rho ,\underline {c}^0)$
such that We choose $$ \begin{align*}G^{\underline{\theta}^0}(\underline{a})\cap \mathrm{Cone}(c^{\underline{\theta}^0}_{\underline{a}^{1,j}},F^{\underline{\theta}^0}_{\underline{c}^j}(L),\alpha)= \emptyset.\end{align*} $$
$$ \begin{align*}G^{\underline{\theta}^0}(\underline{a})\cap \mathrm{Cone}(c^{\underline{\theta}^0}_{\underline{a}^{1,j}},F^{\underline{\theta}^0}_{\underline{c}^j}(L),\alpha)= \emptyset.\end{align*} $$
 $\underline {a}^{2,j}$
as any such element. It easily follows from the choice of
$\underline {a}^{2,j}$
as any such element. It easily follows from the choice of
 $\underline {a}^{2,j}$
that
$\underline {a}^{2,j}$
that  $$ \begin{align*}\measuredangle (c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}, F^{\underline{\theta}^0}_{\underline{c}^j}(L))>\alpha. \end{align*} $$
$$ \begin{align*}\measuredangle (c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}, F^{\underline{\theta}^0}_{\underline{c}^j}(L))>\alpha. \end{align*} $$
Let
![]() $\tilde {L}$
be the line orthogonal to the vector
$\tilde {L}$
be the line orthogonal to the vector
![]() $\beta _1^T \tilde {\xi }$
. The previous inequality and the choice of
$\beta _1^T \tilde {\xi }$
. The previous inequality and the choice of
![]() $\delta _1$
implies that
$\delta _1$
implies that
Now we have all the ingredients to finish the proof. For any j, the pair
![]() $\underline {a}^{1,j}, \underline {a}^{2,j}$
verifies either option (i) or (ii), note that option (ii) implies
$\underline {a}^{1,j}, \underline {a}^{2,j}$
verifies either option (i) or (ii), note that option (ii) implies
 $$ \begin{align*} |c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}| \geq \frac{|\langle \beta_1^T \tilde{\xi}, c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}\rangle|}{ \|\beta_1^T\|\cdot |\tilde{\xi}| } &\geq \pi \|\beta_1\|^{-1}|\tilde{\xi}|^{-1}-2C_3 \|\beta_1\|^{-1}\rho\\ &\geq \frac{\pi \|\beta\|^{-1}}{2}|\tilde{\xi}|^{-1}-4C_3 \|\beta\|^{-1}\rho\\ &\geq \bigg(\frac{\pi \|\beta\|^{-1}}{2n}\Delta_0^{-1} -4C_3 \|\beta\|^{-1}\bigg)\rho. \end{align*} $$
$$ \begin{align*} |c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}| \geq \frac{|\langle \beta_1^T \tilde{\xi}, c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}\rangle|}{ \|\beta_1^T\|\cdot |\tilde{\xi}| } &\geq \pi \|\beta_1\|^{-1}|\tilde{\xi}|^{-1}-2C_3 \|\beta_1\|^{-1}\rho\\ &\geq \frac{\pi \|\beta\|^{-1}}{2}|\tilde{\xi}|^{-1}-4C_3 \|\beta\|^{-1}\rho\\ &\geq \bigg(\frac{\pi \|\beta\|^{-1}}{2n}\Delta_0^{-1} -4C_3 \|\beta\|^{-1}\bigg)\rho. \end{align*} $$
Hence, choosing
![]() $\Delta _0$
small enough, we can guarantee that option (ii) is not verified for
$\Delta _0$
small enough, we can guarantee that option (ii) is not verified for
![]() $j=n-1$
. However, if
$j=n-1$
. However, if
![]() $\underline {a}^{1,j}, \underline {a}^{2,j}$
verifies option (i), then using equation (25), we get
$\underline {a}^{1,j}, \underline {a}^{2,j}$
verifies option (i), then using equation (25), we get
 $$ \begin{align*} |c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}| \cdot \sin (\alpha/2) &\leq |c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}| \cdot \sin \measuredangle (c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}, \tilde{L})\\ &= |c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}| \cdot \cos \measuredangle (c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}, \mathbb{R} \beta_1^T \tilde{\xi})\\ &= \frac{|\langle \beta_1^T \tilde{\xi} , c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}\rangle|}{|\beta_1^T \tilde{\xi}|}\\&\leq \frac{2\eta_5 + 2C_3 |\tilde{\xi}| \rho}{{1}/{2}\|\beta\| \cdot |\tilde{\xi}|}\\ &\leq 4\eta_5 |\tilde{\xi}|^{-1}\|\beta\|^{-1}+4C_3\rho \|\beta\|^{-1}, \end{align*} $$
$$ \begin{align*} |c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}| \cdot \sin (\alpha/2) &\leq |c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}| \cdot \sin \measuredangle (c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}, \tilde{L})\\ &= |c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}| \cdot \cos \measuredangle (c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}, \mathbb{R} \beta_1^T \tilde{\xi})\\ &= \frac{|\langle \beta_1^T \tilde{\xi} , c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}\rangle|}{|\beta_1^T \tilde{\xi}|}\\&\leq \frac{2\eta_5 + 2C_3 |\tilde{\xi}| \rho}{{1}/{2}\|\beta\| \cdot |\tilde{\xi}|}\\ &\leq 4\eta_5 |\tilde{\xi}|^{-1}\|\beta\|^{-1}+4C_3\rho \|\beta\|^{-1}, \end{align*} $$
and we obtain
Hence, assuming
![]() $\eta _5$
and
$\eta _5$
and
![]() $\rho $
small enough, we can guarantee that option (i) is not verified for
$\rho $
small enough, we can guarantee that option (i) is not verified for
![]() $j=0$
. Therefore, there exists j such that
$j=0$
. Therefore, there exists j such that
![]() $\underline {a}^{1,j}, \underline {a}^{2,j}$
verifies option (ii) and
$\underline {a}^{1,j}, \underline {a}^{2,j}$
verifies option (ii) and
![]() $\underline {a}^{1,j+1}, \underline {a}^{2,j+1}$
verifies option (i). From the inequalities obtained, we see that
$\underline {a}^{1,j+1}, \underline {a}^{2,j+1}$
verifies option (i). From the inequalities obtained, we see that
 $$ \begin{align*} \frac{|c^{\underline{\theta}^0}_{\underline{a}^{1,j+1}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j+1}}|}{|c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}|}&\leq \bigg(\sin \frac{\alpha}{2}\bigg)^{-1} \frac{4\eta_5 |\tilde{\xi}|^{-1}\|\beta\|^{-1}+4C_3\rho \|\beta\|^{-1}}{\frac{\pi \|\beta\|^{-1}}{2}|\tilde{\xi}|^{-1}-4C_3\|\beta\|^{-1}\rho}\\ &= \bigg(\sin \frac{\alpha}{2}\bigg)^{-1} \frac{4\eta_5 +4C_3\rho |\tilde{\xi}|}{(\pi /2)-4C_3\rho|\tilde{\xi}|}\\ &\leq \bigg(\sin \frac{\alpha}{2}\bigg)^{-1} \frac{4\eta_5 +4nC_3\Delta_0}{(\pi /2)-4nC_3\Delta_0}, \end{align*} $$
$$ \begin{align*} \frac{|c^{\underline{\theta}^0}_{\underline{a}^{1,j+1}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j+1}}|}{|c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}|}&\leq \bigg(\sin \frac{\alpha}{2}\bigg)^{-1} \frac{4\eta_5 |\tilde{\xi}|^{-1}\|\beta\|^{-1}+4C_3\rho \|\beta\|^{-1}}{\frac{\pi \|\beta\|^{-1}}{2}|\tilde{\xi}|^{-1}-4C_3\|\beta\|^{-1}\rho}\\ &= \bigg(\sin \frac{\alpha}{2}\bigg)^{-1} \frac{4\eta_5 +4C_3\rho |\tilde{\xi}|}{(\pi /2)-4C_3\rho|\tilde{\xi}|}\\ &\leq \bigg(\sin \frac{\alpha}{2}\bigg)^{-1} \frac{4\eta_5 +4nC_3\Delta_0}{(\pi /2)-4nC_3\Delta_0}, \end{align*} $$
where we used
![]() $|\tilde {\xi }|\in [1,n\Delta _0\rho ^{-1}]$
. We obtain
$|\tilde {\xi }|\in [1,n\Delta _0\rho ^{-1}]$
. We obtain
 $$ \begin{align*}\frac{|c^{\underline{\theta}^0}_{\underline{a}^{1,j+1}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j+1}}|}{|c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}|}\leq \left(\sin \frac{\alpha}{2}\right)^{-1} \frac{4\eta_5 +4nC_3\Delta_0}{(\pi /2)-4nC_3\Delta_0},\end{align*} $$
$$ \begin{align*}\frac{|c^{\underline{\theta}^0}_{\underline{a}^{1,j+1}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j+1}}|}{|c^{\underline{\theta}^0}_{\underline{a}^{1,j}}-c^{\underline{\theta}^0}_{\underline{a}^{2,j}}|}\leq \left(\sin \frac{\alpha}{2}\right)^{-1} \frac{4\eta_5 +4nC_3\Delta_0}{(\pi /2)-4nC_3\Delta_0},\end{align*} $$
notice that the right-hand side of the inequality goes to zero as
![]() $\Delta _0$
and
$\Delta _0$
and
![]() $\eta _5$
go to zero; however, the left-hand side is bounded away from zero thanks to the bounded geometry of the Cantor set
$\eta _5$
go to zero; however, the left-hand side is bounded away from zero thanks to the bounded geometry of the Cantor set
![]() $K_{j_0}$
. We conclude that for
$K_{j_0}$
. We conclude that for
![]() $\Delta _0$
small enough,
$\Delta _0$
small enough,
![]() $\eta _5$
is bounded away from zero, as we wanted to prove.
$\eta _5$
is bounded away from zero, as we wanted to prove.
5 Final remarks
In this final section, we want to comment, very briefly and without details, about our work in progress, together with Araujo, about a complex version of Palis’s conjecture on the arithmetic difference of Cantor sets.
More precisely, given a pair of conformal Cantor sets
![]() $(K,K')$
with
$(K,K')$
with
![]() $HD(K)+HD(K')>2$
, we are close to prove that arbitrarily close to this pair, we can find another pair
$HD(K)+HD(K')>2$
, we are close to prove that arbitrarily close to this pair, we can find another pair
![]() $(\tilde {K}, \tilde {K}')$
such that
$(\tilde {K}, \tilde {K}')$
such that
![]() $int(\tilde {K}-\tilde {K}')\neq \emptyset $
.
$int(\tilde {K}-\tilde {K}')\neq \emptyset $
.
To make sense of the previous statement, we need to explain the topology in the space of Cantor sets. Fix a set of letters
![]() $\mathbb {A}$
and admissible pairs
$\mathbb {A}$
and admissible pairs
![]() $B\subset \mathbb {A}\times \mathbb {A}$
, so that they generate a subshift of finite type
$B\subset \mathbb {A}\times \mathbb {A}$
, so that they generate a subshift of finite type
![]() $\Sigma ^+$
. Denote by
$\Sigma ^+$
. Denote by
![]() $\Omega _{\Sigma ^+}^m$
the set of all conformal
$\Omega _{\Sigma ^+}^m$
the set of all conformal
![]() $C^m$
Cantor sets with the same associated subshift
$C^m$
Cantor sets with the same associated subshift
![]() $\Sigma ^+$
. We introduce a topology in this space by defining a basis of neighborhoods. For each
$\Sigma ^+$
. We introduce a topology in this space by defining a basis of neighborhoods. For each
![]() $K\in \Omega _{\Sigma ^+}^m$
and
$K\in \Omega _{\Sigma ^+}^m$
and
![]() $\delta>0$
, we define the
$\delta>0$
, we define the
![]() $\delta $
-neighborhood around K as the set of
$\delta $
-neighborhood around K as the set of
![]() $C^m$
conformal Cantor sets
$C^m$
conformal Cantor sets
![]() $K'$
defined by an expanding map
$K'$
defined by an expanding map
![]() $g':V'\to \mathbb {C}$
,
$g':V'\to \mathbb {C}$
,
![]() $\sqcup _{a}G'(a)\subset V'$
such that
$\sqcup _{a}G'(a)\subset V'$
such that
![]() $G'(a)\subset V_{\delta }(G(a))$
for every
$G'(a)\subset V_{\delta }(G(a))$
for every
![]() $a\in \mathbb {A}$
(where
$a\in \mathbb {A}$
(where
![]() $V_{\delta }(G(a))$
refers to the
$V_{\delta }(G(a))$
refers to the
![]() $\delta $
-neighborhood of
$\delta $
-neighborhood of
![]() $G(a)$
) and the restrictions to
$G(a)$
) and the restrictions to
![]() $V\cap V'$
of the functions g,
$V\cap V'$
of the functions g,
![]() $g'$
are
$g'$
are
![]() $\delta $
close in the
$\delta $
close in the
![]() $C^m$
topology.
$C^m$
topology.
The definition of this topology is similar to that for regular Cantor sets in the real line; moreover, it verifies that if we have regular conformal Cantor sets associated to horseshoes for automorphisms of
![]() $\mathbb {C}^2$
(as considered in [Reference Araújo and Moreira1]), then those Cantor sets depend continuously on the automorphisms.
$\mathbb {C}^2$
(as considered in [Reference Araújo and Moreira1]), then those Cantor sets depend continuously on the automorphisms.
Our proof follows the strategy of [Reference Moreira and Yoccoz7] adapted to conformal Cantor sets. We prove the existence of a recurrent compact set for a pair
![]() $(\tilde {K}, \tilde {K}')$
close to the original pair. The perturbed pair
$(\tilde {K}, \tilde {K}')$
close to the original pair. The perturbed pair
![]() $(\tilde {K}, \tilde {K}')$
is selected, within a family of possible perturbations, using a probabilistic argument. To be able to perturb properly, we use the fact that in the definition of conformal Cantor sets, the derivative
$(\tilde {K}, \tilde {K}')$
is selected, within a family of possible perturbations, using a probabilistic argument. To be able to perturb properly, we use the fact that in the definition of conformal Cantor sets, the derivative
![]() $Dg$
is conformal at the Cantor set and this is only required at these points. The not essentially real hypothesis also plays an important role in this part.
$Dg$
is conformal at the Cantor set and this is only required at these points. The not essentially real hypothesis also plays an important role in this part.
For the construction of the recurrent compact set, we first define a set of ‘good’ scales, and for this, we use a complex version of Marstrand’s projection theorem together with the scale recurrence lemma we proved in these pages. The conformal version of the scale recurrence lemma is a key tool for our proof of a complex version of Palis’s conjecture.
Acknowledgements
This work was supported by CNPq and CAPES. Part of this work was done while A.M.Z. was a Postdoc at UFRJ.