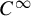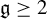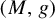1 Introduction
Assume that
![]() $(M,g)$
is a smooth, connected, and closed manifold equipped with a
$(M,g)$
is a smooth, connected, and closed manifold equipped with a
![]() $C^{\infty }$
Riemannian metric g. The geodesic flow
$C^{\infty }$
Riemannian metric g. The geodesic flow
![]() $g^t$
, generated by the Riemannian metric g, is defined on the unit tangent bundle
$g^t$
, generated by the Riemannian metric g, is defined on the unit tangent bundle
![]() $SM$
by the formula:
$SM$
by the formula:
where
![]() $\gamma ^{\prime }_v(t)$
is the unit vector tangent to the geodesic
$\gamma ^{\prime }_v(t)$
is the unit vector tangent to the geodesic
![]() $\gamma _v(t)$
uniquely determined by the initial vector
$\gamma _v(t)$
uniquely determined by the initial vector
![]() $v\in SM$
. In this paper, we study the ergodicity of the geodesic flow with respect to the Liouville measure
$v\in SM$
. In this paper, we study the ergodicity of the geodesic flow with respect to the Liouville measure
![]() $\nu $
on
$\nu $
on
![]() $SM$
, where
$SM$
, where
![]() $(M,g)$
is assumed to be a surface of genus
$(M,g)$
is assumed to be a surface of genus
![]() $\mathfrak {g} \geq 2$
having no focal points.
$\mathfrak {g} \geq 2$
having no focal points.
Our work was originally inspired by the classical results on the ergodicity of the geodesic flows on Riemannian manifolds with non-positive curvature. The geodesic flows on Riemannian manifolds with negative or non-positive curvature have very rich dynamics and broad applications. In the last century, this class of geodesic flows have always been attracting the interest of mathematicians in dynamical systems and related areas. Many beautiful results on the dynamics of the geodesic flows have been exhibited. Among which, the ergodic properties, such as the ergodicity and the mixing properties, the measure of maximal entropy, etc., have a special importance and receive extensive attention. The statistical properties of geodesic flows on surfaces with negative curvature were first studied by Hadamard and Morse in the beginning of the twentieth century. Hopf [Reference Hopf16, Reference Hopf17] proved the ergodicity of the geodesic flow with respect to the Liouville measure
![]() $\nu $
on
$\nu $
on
![]() $SM$
for compact surfaces of variable negative curvature and for compact manifolds of constant negative sectional curvature in any dimension. The general case for compact manifolds of variable negative curvature was established by Anosov and Sinai [Reference Anosov1, Reference Anosov and Sinai2]. The geodesic flows on compact manifolds of negative curvature is a primary example of the uniformly hyperbolic flows (or Anosov flows). Its ergodicity was established based on the classical Hopf argument and results in hyperbolic geometry (see, for example, the appendix in [Reference Ballmann3]).
$SM$
for compact surfaces of variable negative curvature and for compact manifolds of constant negative sectional curvature in any dimension. The general case for compact manifolds of variable negative curvature was established by Anosov and Sinai [Reference Anosov1, Reference Anosov and Sinai2]. The geodesic flows on compact manifolds of negative curvature is a primary example of the uniformly hyperbolic flows (or Anosov flows). Its ergodicity was established based on the classical Hopf argument and results in hyperbolic geometry (see, for example, the appendix in [Reference Ballmann3]).
Geodesic flows on manifolds of non-positive curvature have also been intensively studied since the 1970’s. However, even for surfaces of non-positive curvature, the geodesic flows present certain non-uniformly hyperbolic behaviors. The ergodicity for the geodesic flows faces a great challenge due to the existence of ‘flat’ geodesics. Consider a closed surface M of genus
![]() $\mathfrak {g} \geq 2$
and of non-positive curvature. Let
$\mathfrak {g} \geq 2$
and of non-positive curvature. Let
where K denotes the curvature of the point. We call
![]() $\gamma _v$
a flat geodesic if
$\gamma _v$
a flat geodesic if
![]() $v\in \Lambda $
, that is,
$v\in \Lambda $
, that is,
![]() $\gamma _v$
is a flat geodesic if the curvature along it is constantly
$\gamma _v$
is a flat geodesic if the curvature along it is constantly
![]() $0$
. It is still not known if
$0$
. It is still not known if
![]() $\Lambda $
is small in measure (
$\Lambda $
is small in measure (
![]() $\nu (\Lambda )=0$
or not), in general. However, from the dynamical point of view,
$\nu (\Lambda )=0$
or not), in general. However, from the dynamical point of view,
![]() $\Lambda $
should be a very small set. For example, in [Reference Knieper20], Knieper showed the strict inequality for geodesic flows on rank
$\Lambda $
should be a very small set. For example, in [Reference Knieper20], Knieper showed the strict inequality for geodesic flows on rank
![]() $1$
manifolds of non-positive curvature:
$1$
manifolds of non-positive curvature:
where
![]() $g^1$
is the time-one map of the geodesic flow
$g^1$
is the time-one map of the geodesic flow
![]() $g^t$
, h denotes the topological entropy, and
$g^t$
, h denotes the topological entropy, and
![]() $\Lambda $
denotes the irregular set of the geodesic flow, which is a counterpart of the above defined set in arbitrary dimensions. This means that the geodesic flow restricted on
$\Lambda $
denotes the irregular set of the geodesic flow, which is a counterpart of the above defined set in arbitrary dimensions. This means that the geodesic flow restricted on
![]() $\Lambda $
has less complexity than the whole geodesic flow. Knieper [Reference Knieper20] (see also [Reference Burns and Gelfert7]) proved that on rank-
$\Lambda $
has less complexity than the whole geodesic flow. Knieper [Reference Knieper20] (see also [Reference Burns and Gelfert7]) proved that on rank-
![]() $1$
surfaces of non-positive curvature, the geodesic flow on
$1$
surfaces of non-positive curvature, the geodesic flow on
![]() $\Lambda $
has zero topological entropy. In higher dimensions, it is possible to have positive entropy on
$\Lambda $
has zero topological entropy. In higher dimensions, it is possible to have positive entropy on
![]() $\Lambda $
; an example was given by Gromov [Reference Gromov15].
$\Lambda $
; an example was given by Gromov [Reference Gromov15].
For geodesic flows on rank-
![]() $1$
surfaces of non-positive curvature, the orbits inside
$1$
surfaces of non-positive curvature, the orbits inside
![]() $\Lambda $
are also believed to have a simple behavior. In all the known examples, all the orbits in
$\Lambda $
are also believed to have a simple behavior. In all the known examples, all the orbits in
![]() $\Lambda $
are closed. In a recent survey, Burns asks the question: Does there exist a non-closed flat geodesic? [Reference Burns and Matveev8, Question 6.2.1]. In this paper, we will show that all flat geodesics are closed on surfaces without focal points, under our assumption. Nevertheless, the most important topic on the set
$\Lambda $
are closed. In a recent survey, Burns asks the question: Does there exist a non-closed flat geodesic? [Reference Burns and Matveev8, Question 6.2.1]. In this paper, we will show that all flat geodesics are closed on surfaces without focal points, under our assumption. Nevertheless, the most important topic on the set
![]() $\Lambda $
is still its Liouville measure (that is, how small it is). One expects that on surfaces with non-positive curvature,
$\Lambda $
is still its Liouville measure (that is, how small it is). One expects that on surfaces with non-positive curvature,
![]() $\Lambda $
should have
$\Lambda $
should have
![]() $0$
Liouville measure (this leads to the ergodicity of the geodesic flows, see [Reference Barreira and Pesin5]). This is the following well-known conjecture on the ergodicity for geodesic flows on surfaces with non-positive curvature. (Some experts in the area expect a negative answer to the conjecture. Our results in the paper support the conjecture under an additional assumption.)
$0$
Liouville measure (this leads to the ergodicity of the geodesic flows, see [Reference Barreira and Pesin5]). This is the following well-known conjecture on the ergodicity for geodesic flows on surfaces with non-positive curvature. (Some experts in the area expect a negative answer to the conjecture. Our results in the paper support the conjecture under an additional assumption.)
Conjecture 1.1. (Cf. [Reference Rodriguez Hertz22])
Let
![]() $(M,g)$
be a smooth, connected, and closed surface of genus
$(M,g)$
be a smooth, connected, and closed surface of genus
![]() $\mathfrak {g}\geq 2$
, which has non-positive curvature. Then all flat geodesics are closed and there are only finitely many homotopy classes of such geodesics. In particular,
$\mathfrak {g}\geq 2$
, which has non-positive curvature. Then all flat geodesics are closed and there are only finitely many homotopy classes of such geodesics. In particular,
![]() $\nu (\Lambda )=0$
, and hence the geodesic flow on
$\nu (\Lambda )=0$
, and hence the geodesic flow on
![]() $SM$
is ergodic.
$SM$
is ergodic.
We declare that the terminology ‘ergodicity’ in this paper means the ergodicity with respect to the Liouville measure
![]() $\nu $
on
$\nu $
on
![]() $SM$
. The problem we are considering in this paper is the ergodicity of the geodesic flows on surfaces without focal points. First of all, we give the definition of the focal points.
$SM$
. The problem we are considering in this paper is the ergodicity of the geodesic flows on surfaces without focal points. First of all, we give the definition of the focal points.
Definition 1.2. Let
![]() $(M,g)$
be a Riemannian manifold and
$(M,g)$
be a Riemannian manifold and
![]() $\gamma $
a geodesic on M. Points
$\gamma $
a geodesic on M. Points
![]() $q=\gamma (t_{0})$
and
$q=\gamma (t_{0})$
and
![]() $p=\gamma (t_{1})$
are called focal if there exists a Jacobi field J along
$p=\gamma (t_{1})$
are called focal if there exists a Jacobi field J along
![]() $\gamma $
such that
$\gamma $
such that
![]() $J(t_{0})=0$
,
$J(t_{0})=0$
,
![]() $J'(t_{0})\neq 0$
, and
$J'(t_{0})\neq 0$
, and
![]() ${d}/{dt}\| J(t)\|^{2}\mid _{t=t_{1}}=0$
. The Riemannian manifold
${d}/{dt}\| J(t)\|^{2}\mid _{t=t_{1}}=0$
. The Riemannian manifold
![]() $(M,g)$
is said to be without focal points if there are no focal points on any geodesic of M.
$(M,g)$
is said to be without focal points if there are no focal points on any geodesic of M.
It is not hard to see that the manifolds with non-positive curvature have no focal points. If M is a surface of genus
![]() $1$
and has no focal points, then it must be a flat torus [Reference Burago and Ivanov6, Reference Hopf18]. Therefore, the geodesic flow on M is obviously not ergodic. However, if M has higher genus, the curvature is allowed to vary. In this paper, we always assume that the surface M we are considering has genus greater than
$1$
and has no focal points, then it must be a flat torus [Reference Burago and Ivanov6, Reference Hopf18]. Therefore, the geodesic flow on M is obviously not ergodic. However, if M has higher genus, the curvature is allowed to vary. In this paper, we always assume that the surface M we are considering has genus greater than
![]() $1$
.
$1$
.
In the 1970’s, by using his theory of non-uniform hyperbolicity, Pesin obtained a celebrated result on the ergodicity of the geodesic flows on manifolds without focal points, which satisfy the uniform visibility axiom [Reference Barreira and Pesin5, Theorem 12.2.12]. We are not going to give the explicit definition of the uniform visibility axiom here, but remark that it is satisfied by every closed surface of genus
![]() $\mathfrak {g}\geq 1$
. To state Pesin’s result for surfaces without focal points, we define the sets:
$\mathfrak {g}\geq 1$
. To state Pesin’s result for surfaces without focal points, we define the sets:
 $$ \begin{align*}\Delta^+&:=\{v\in SM: \chi(v,\xi)<0 \text{ for any } \xi\in E^+(v)\},\\\Delta^-&:=\{v\in SM: \chi(v,\xi)>0 \text{ for any } \xi\in E^-(v)\},\\\Delta&:=\Delta^+\cap \Delta^-,\end{align*} $$
$$ \begin{align*}\Delta^+&:=\{v\in SM: \chi(v,\xi)<0 \text{ for any } \xi\in E^+(v)\},\\\Delta^-&:=\{v\in SM: \chi(v,\xi)>0 \text{ for any } \xi\in E^-(v)\},\\\Delta&:=\Delta^+\cap \Delta^-,\end{align*} $$
where
![]() $\chi $
denotes the Lyapunov exponents and
$\chi $
denotes the Lyapunov exponents and
![]() $E^{\pm }$
denotes the stable and unstable distributions on
$E^{\pm }$
denotes the stable and unstable distributions on
![]() $SM$
with respect to the geodesic flow, respectively. Here,
$SM$
with respect to the geodesic flow, respectively. Here,
![]() $\Delta $
is called the regular set with respect to the geodesic flow. For details, see §2. Pesin proved the following theorem.
$\Delta $
is called the regular set with respect to the geodesic flow. For details, see §2. Pesin proved the following theorem.
Theorem 1.3. (Cf. [Reference Barreira and Pesin5])
For the geodesic flow on a surface without focal points, we have that
![]() $\nu (\Delta )>0$
, and
$\nu (\Delta )>0$
, and
![]() $g^t|_{\Delta }$
is ergodic.
$g^t|_{\Delta }$
is ergodic.
Our first result in this paper is the following relation between the regular set
![]() $\Delta $
and the set
$\Delta $
and the set
![]() $\Lambda $
of unit vectors tangent to flat geodesics. We remark that all our results are established under the assumption of no focal points so, sometimes, we omit the statement of this assumption in the following theorems.
$\Lambda $
of unit vectors tangent to flat geodesics. We remark that all our results are established under the assumption of no focal points so, sometimes, we omit the statement of this assumption in the following theorems.
Theorem 1.4.
![]() $\nu (\Lambda ^c \setminus \Delta )=0$
.
$\nu (\Lambda ^c \setminus \Delta )=0$
.
By Theorems 1.3 and 1.4, if
![]() $\nu (\Lambda )=0$
, the regular set
$\nu (\Lambda )=0$
, the regular set
![]() $\Delta \subset SM$
is a full measure set and then the geodesic flow is ergodic on
$\Delta \subset SM$
is a full measure set and then the geodesic flow is ergodic on
![]() $SM$
. The condition
$SM$
. The condition
![]() $\nu (\Lambda )=0$
holds in all the known examples so far. However, it is still not proved, even for the surfaces of non-positive curvature. Recent progress on this problem was made by the first author in [Reference Wu25]. We conclude the main result of [Reference Wu25] in the following theorem.
$\nu (\Lambda )=0$
holds in all the known examples so far. However, it is still not proved, even for the surfaces of non-positive curvature. Recent progress on this problem was made by the first author in [Reference Wu25]. We conclude the main result of [Reference Wu25] in the following theorem.
Theorem 1.5. (Cf. [Reference Wu25])
Let
![]() $(M,g)$
be a smooth, connected, and closed surface of genus
$(M,g)$
be a smooth, connected, and closed surface of genus
![]() $\mathfrak {g}\geq 2$
, which has non-positive curvature. Suppose that the set
$\mathfrak {g}\geq 2$
, which has non-positive curvature. Suppose that the set
![]() $\{p\in M: K(p)<0\}$
has finitely many connected components, then
$\{p\in M: K(p)<0\}$
has finitely many connected components, then
![]() $\nu (\Lambda )=0$
. In particular, the geodesic flow is ergodic.
$\nu (\Lambda )=0$
. In particular, the geodesic flow is ergodic.
In this paper, we generalize Theorem 1.5 from the setting of surfaces with non-positive curvature to surfaces without focal points. This means that we are going to prove the ergodicity of the geodesic flows on surfaces which can have positive curvature in a subset. To achieve this goal, we explore the properties of flat geodesics, which are also of independent interest. Among them is the following result. Here, we let
![]() $\text {Per}(g^t)$
denote the set of periodic points of the geodesic flow and
$\text {Per}(g^t)$
denote the set of periodic points of the geodesic flow and
![]() $\mathcal {O}(z)$
denote the orbit of z under the geodesic flow. The following theorem says that non-closed flat orbits can accumulate only on non-closed flat orbits.
$\mathcal {O}(z)$
denote the orbit of z under the geodesic flow. The following theorem says that non-closed flat orbits can accumulate only on non-closed flat orbits.
Theorem 1.6.
![]() $\Lambda \cap (\text {Per } (g^t))^c$
is a closed subset of
$\Lambda \cap (\text {Per } (g^t))^c$
is a closed subset of
![]() $SM$
.
$SM$
.
According to the dichotomy: (1)
![]() $\Lambda \subset \text {Per}(g^t)$
; (2)
$\Lambda \subset \text {Per}(g^t)$
; (2)
![]() $\Lambda \cap (\text {Per } (g^t))^c \neq \emptyset $
, and we prove the following two results.
$\Lambda \cap (\text {Per } (g^t))^c \neq \emptyset $
, and we prove the following two results.
Theorem 1.7. If
![]() $\Lambda \subset \text {Per}(g^t)$
, then there is a finite decomposition of
$\Lambda \subset \text {Per}(g^t)$
, then there is a finite decomposition of
![]() $\Lambda $
:
$\Lambda $
:
where each
![]() $\mathcal {O}_i, 1\leq i \leq k$
, is an isolated periodic orbit and each
$\mathcal {O}_i, 1\leq i \leq k$
, is an isolated periodic orbit and each
![]() $\mathcal {F}_j, 1\leq j \leq l$
, consists of vectors tangent to a flat strip. Here, k or l is allowed to be
$\mathcal {F}_j, 1\leq j \leq l$
, consists of vectors tangent to a flat strip. Here, k or l is allowed to be
![]() $0$
if there is no isolated closed flat geodesic or no flat strip.
$0$
if there is no isolated closed flat geodesic or no flat strip.
We remark that if
![]() $\Lambda \subset \text {Per}(g^t)$
, then Theorem 1.7 immediately implies
$\Lambda \subset \text {Per}(g^t)$
, then Theorem 1.7 immediately implies
![]() $\nu (\Lambda )=0$
, and therefore the geodesic flow is ergodic.
$\nu (\Lambda )=0$
, and therefore the geodesic flow is ergodic.
Theorem 1.8. If
![]() $\Lambda \cap (\text {Per} (g^t))^c \neq \emptyset $
, then there exist
$\Lambda \cap (\text {Per} (g^t))^c \neq \emptyset $
, then there exist
![]() $y, z \in \Lambda $
,
$y, z \in \Lambda $
,
![]() $y\notin \mathcal {O} (z)$
, such that
$y\notin \mathcal {O} (z)$
, such that
Our main result is the following theorem, which means that under certain conditions, the scenario in Theorem 1.8 cannot happen.
Theorem 1.9. If the set
![]() $\{p\in M: K(p)<0\}$
has at most finitely many connected components, then
$\{p\in M: K(p)<0\}$
has at most finitely many connected components, then
![]() $\Lambda \subset \text {Per}(g^t)$
. In particular, the geodesic flow is ergodic.
$\Lambda \subset \text {Per}(g^t)$
. In particular, the geodesic flow is ergodic.
Theorem 1.9 gives a negative answer to Question 6.2.1 asked by Burns in [Reference Burns and Matveev8] for surfaces without focal points when
![]() $\{p\in M: K(p)<0\}$
has at most finitely many connected components. Furthermore, Theorem 1.7 exhibits that in fact there are at most finitely many flat strips and isolated closed flat geodesics in this case.
$\{p\in M: K(p)<0\}$
has at most finitely many connected components. Furthermore, Theorem 1.7 exhibits that in fact there are at most finitely many flat strips and isolated closed flat geodesics in this case.
So far, it is still unknown whether Conjecture 1.1 is true or not in general. In §4, we discover several properties of the flat geodesics on surfaces without focal points, which include:
-
• all flat strips are closed;
-
• a unit vector not tangent to a flat strip has the expansivity property;
-
• an ideal triangle with a flat geodesic which is asymptotic to a closed geodesic as an edge has infinite area.
All these results together with our Theorem 1.6 are believed to be important toward Conjecture 1.1 in future research.
The paper is organized as follows. In §2, we will present some preliminaries on the geodesic flows on surfaces without focal points. The proof of Theorem 1.4 is shown in §3. In §4, we prove Theorem 1.6 and the above properties of the flat geodesics. Our main Theorems 1.7, 1.8, and 1.9 are proved in the last section. Throughout the remainder of the paper, we always let M be a smooth, connected, and closed surface with genus
![]() $\mathfrak {g} \geq 2$
, and equipped with a
$\mathfrak {g} \geq 2$
, and equipped with a
![]() $C^{\infty }$
Riemannian metric g without focal points.
$C^{\infty }$
Riemannian metric g without focal points.
2 Preliminaries on surfaces without focal points
2.1 Jacobi fields, and stable and unstable distributions
To study the dynamics of geodesic flows, we should investigate the geometry of the second tangent bundle
![]() $TTM$
. Let
$TTM$
. Let
![]() $\pi :TM\rightarrow M$
be the natural projection, that is,
$\pi :TM\rightarrow M$
be the natural projection, that is,
![]() $\pi (v)=p$
, where
$\pi (v)=p$
, where
![]() $v \in T_{p}M$
. The connection map
$v \in T_{p}M$
. The connection map
![]() $K_{v}:T_{v}TM\rightarrow T_{\pi (v)}M$
is defined as follows. For any
$K_{v}:T_{v}TM\rightarrow T_{\pi (v)}M$
is defined as follows. For any
![]() $\xi \in T_vTM$
,
$\xi \in T_vTM$
,
![]() $K_{v}\xi := (\nabla X)(t)|_{t=0}$
, where
$K_{v}\xi := (\nabla X)(t)|_{t=0}$
, where
![]() $X:(-\epsilon ,\epsilon )\rightarrow TM$
is a smooth curve satisfying
$X:(-\epsilon ,\epsilon )\rightarrow TM$
is a smooth curve satisfying
![]() $X(0)=v$
and
$X(0)=v$
and
![]() $X'(0)=\xi $
, and
$X'(0)=\xi $
, and
![]() $\nabla $
is the covariant derivative along the curve
$\nabla $
is the covariant derivative along the curve
![]() $\pi (X(t))\subset M$
. Then the standard Sasaki metric on
$\pi (X(t))\subset M$
. Then the standard Sasaki metric on
![]() $TTM$
is given by
$TTM$
is given by
Recall that the Jacobi equation along a geodesic
![]() $\gamma _v(t)$
is
$\gamma _v(t)$
is
where R is the curvature tensor, and
![]() $J(t)$
is a Jacobi field along
$J(t)$
is a Jacobi field along
![]() $\gamma _v(t)$
and perpendicular to
$\gamma _v(t)$
and perpendicular to
![]() $\gamma ^{\prime }_v(t)$
. Suppose
$\gamma ^{\prime }_v(t)$
. Suppose
![]() $J_{\xi }(t)$
is the solution of equation (1) which satisfies the initial conditions
$J_{\xi }(t)$
is the solution of equation (1) which satisfies the initial conditions
 $$ \begin{align*}J_{\xi}(0)=d\pi_{v}\xi,\quad \frac{d}{dt}\bigg|_{t=0}J_{\xi}(t)=K_{v}\xi.\end{align*} $$
$$ \begin{align*}J_{\xi}(0)=d\pi_{v}\xi,\quad \frac{d}{dt}\bigg|_{t=0}J_{\xi}(t)=K_{v}\xi.\end{align*} $$
Then, it follows that (cf. [Reference Barreira and Pesin5, p. 386])
On the surface M, we have the Fermi coordinates
![]() $\{e_1(t), e_2(t)\}$
along the geodesic
$\{e_1(t), e_2(t)\}$
along the geodesic
![]() $\gamma _v(t)$
, obtained by the time t-parallel translations along
$\gamma _v(t)$
, obtained by the time t-parallel translations along
![]() $\gamma _v(t)$
of an orthonormal basis
$\gamma _v(t)$
of an orthonormal basis
![]() $\{e_1(0), e_2(0)\}$
where
$\{e_1(0), e_2(0)\}$
where
![]() $e_1(0)=\gamma ^{\prime }_v(0)$
. Thus,
$e_1(0)=\gamma ^{\prime }_v(0)$
. Thus,
![]() $e_1(t)=\gamma ^{\prime }_v(t)$
and
$e_1(t)=\gamma ^{\prime }_v(t)$
and
![]() $e_2(t) \perp \gamma ^{\prime }_v(t)$
. Suppose that
$e_2(t) \perp \gamma ^{\prime }_v(t)$
. Suppose that
![]() $J(t)=j(t)e_2(t).$
Then the Jacobi equation (1) becomes
$J(t)=j(t)e_2(t).$
Then the Jacobi equation (1) becomes
where
![]() $K(t)=K(\gamma _v(t))$
is the curvature at point
$K(t)=K(\gamma _v(t))$
is the curvature at point
![]() $\gamma _v(t)$
. Let
$\gamma _v(t)$
. Let
![]() $u(t)=j'(t)/j(t)$
. Then the Jacobi equation (2) can be written in an equivalent form
$u(t)=j'(t)/j(t)$
. Then the Jacobi equation (2) can be written in an equivalent form
which is called the Riccati equation.
Using the Fermi coordinates, we can write equation (1) in the matrix form
The following result is a standard fact.
Proposition 2.1. (Cf. [Reference Eberlein12])
Given
![]() $s\in \mathbb {R}$
, let
$s\in \mathbb {R}$
, let
![]() $A_{s}(t)$
be the unique solution of equation (4) satisfying
$A_{s}(t)$
be the unique solution of equation (4) satisfying
![]() $A_{s}(0)=\mathrm {Id}$
and
$A_{s}(0)=\mathrm {Id}$
and
![]() $A_{s}(s)=0$
, then there exists a limit
$A_{s}(s)=0$
, then there exists a limit
 $$ \begin{align*}A^{+}=\lim_{s\rightarrow +\infty}\frac{d}{dt}\bigg|_{t=0}A_{s}(t).\end{align*} $$
$$ \begin{align*}A^{+}=\lim_{s\rightarrow +\infty}\frac{d}{dt}\bigg|_{t=0}A_{s}(t).\end{align*} $$
Now we can define the positive limit solution
![]() $A^+(t)$
as the solution of equation (4) satisfying the initial conditions
$A^+(t)$
as the solution of equation (4) satisfying the initial conditions
 $$ \begin{align*}A^{+}(0)=\mathrm{Id}, \quad \frac{d}{dt}\bigg|_{t=0}A^{+}(t)=A^{+}.\end{align*} $$
$$ \begin{align*}A^{+}(0)=\mathrm{Id}, \quad \frac{d}{dt}\bigg|_{t=0}A^{+}(t)=A^{+}.\end{align*} $$
It is easy to see that
![]() $A^{+}(t)$
is non-degenerate for all
$A^{+}(t)$
is non-degenerate for all
![]() $t\in \mathbb {R}$
. Similarly, letting
$t\in \mathbb {R}$
. Similarly, letting
![]() $s \rightarrow -\infty $
, one can define the negative limit solution
$s \rightarrow -\infty $
, one can define the negative limit solution
![]() $A^{-}(t)$
of equation (4).
$A^{-}(t)$
of equation (4).
For each
![]() $v \in SM$
, define
$v \in SM$
, define
 $$ \begin{align*}E^{+}(v)&:=\{\xi \in T_{v}SM: \langle\xi,V(v)\rangle=0 \text{ and } J_{\xi}(t)=A^{+}(t)\,d\pi_{v}\xi\},\\E^{-}(v)&:=\{\xi \in T_{v}SM: \langle\xi,V(v)\rangle=0 \text{ and } J_{\xi}(t)=A^{-}(t)\,d\pi_{v}\xi\},\end{align*} $$
$$ \begin{align*}E^{+}(v)&:=\{\xi \in T_{v}SM: \langle\xi,V(v)\rangle=0 \text{ and } J_{\xi}(t)=A^{+}(t)\,d\pi_{v}\xi\},\\E^{-}(v)&:=\{\xi \in T_{v}SM: \langle\xi,V(v)\rangle=0 \text{ and } J_{\xi}(t)=A^{-}(t)\,d\pi_{v}\xi\},\end{align*} $$
where V is the vector field generated by the geodesic flow and
![]() $J_{\xi }$
is the solution of equation (1) satisfying
$J_{\xi }$
is the solution of equation (1) satisfying
 $$ \begin{align*}J_{\xi}(0)=d\pi_{v}\xi,\ ~~\frac{d}{dt}\bigg|_{t=0}J_{\xi}(t)=K_{v}\xi.\end{align*} $$
$$ \begin{align*}J_{\xi}(0)=d\pi_{v}\xi,\ ~~\frac{d}{dt}\bigg|_{t=0}J_{\xi}(t)=K_{v}\xi.\end{align*} $$
One can check the following properties of
![]() $E^{+}(v)$
and
$E^{+}(v)$
and
![]() $E^{-}(v)$
(see [Reference Barreira and Pesin5] for more details).
$E^{-}(v)$
(see [Reference Barreira and Pesin5] for more details).
Proposition 2.2. (Cf. [Reference Barreira and Pesin5, Proposition 12.1.1])
![]() $E^{+}(v)$
and
$E^{+}(v)$
and
![]() $E^{-}(v)$
have the following properties.
$E^{-}(v)$
have the following properties.
-
(1)
 $E^{+}(v)$
and
$E^{+}(v)$
and
 $E^{-}(v)$
are one-dimensional subspaces of
$E^{-}(v)$
are one-dimensional subspaces of
 $T_{v}SM$
.
$T_{v}SM$
. -
(2)
 $d\pi _{v}E^{+}(v)=d\pi _{v}E^{-}(v)=\{w \in T_{\pi (v)}M: w \text { is orthogonal to } v\}$
.
$d\pi _{v}E^{+}(v)=d\pi _{v}E^{-}(v)=\{w \in T_{\pi (v)}M: w \text { is orthogonal to } v\}$
. -
(3) The subspaces
 $E^{+}(v)$
and
$E^{+}(v)$
and
 $E^{-}(v)$
are continuous and invariant under the geodesic flow.
$E^{-}(v)$
are continuous and invariant under the geodesic flow. -
(4) Let
 $\tau : SM \rightarrow SM$
be the involution defined by
$\tau : SM \rightarrow SM$
be the involution defined by
 $\tau v=-v$
, then
$\tau v=-v$
, then  $$ \begin{align*}E^{+}(-v)=d\tau E^{-}(v) \quad\text{and}\quad E^{-}(-v)=d\tau E^{+}(v).\end{align*} $$
$$ \begin{align*}E^{+}(-v)=d\tau E^{-}(v) \quad\text{and}\quad E^{-}(-v)=d\tau E^{+}(v).\end{align*} $$
-
(5) If the curvature satisfies
 $K(p) \geq -a^{2}$
for some
$K(p) \geq -a^{2}$
for some
 $a> 0$
, then
$a> 0$
, then
 $\|K_{v}\xi \| \leq a \|d\pi _{v}\xi \|$
for any
$\|K_{v}\xi \| \leq a \|d\pi _{v}\xi \|$
for any
 $\xi \in E^{+}(v)$
or
$\xi \in E^{+}(v)$
or
 $\xi \in E^{-}(v)$
.
$\xi \in E^{-}(v)$
. -
(6) If
 $\xi \in E^{+}(v)$
or
$\xi \in E^{+}(v)$
or
 $\xi \in E^{-}(v)$
, then
$\xi \in E^{-}(v)$
, then
 $J_{\xi }(t)\neq 0$
for each
$J_{\xi }(t)\neq 0$
for each
 $t \in \mathbb {R}$
.
$t \in \mathbb {R}$
. -
(7)
 $\xi \in E^{+}(v)$
(respectively,
$\xi \in E^{+}(v)$
(respectively,
 $\xi \in E^{-}(v)$
) if and only if
$\xi \in E^{-}(v)$
) if and only if  $$ \begin{align*}\langle\xi,V(v)\rangle=0 \quad\text{and}\quad \|d\pi_{g^{t}v}dg^{t}_{v}\xi\| \leq c\end{align*} $$
$$ \begin{align*}\langle\xi,V(v)\rangle=0 \quad\text{and}\quad \|d\pi_{g^{t}v}dg^{t}_{v}\xi\| \leq c\end{align*} $$
for each
 $t> 0$
(respectively,
$t> 0$
(respectively,
 $t < 0$
) and some
$t < 0$
) and some
 $c> 0$
.
$c> 0$
. -
(8) For
 $\xi \in E^{+}(v)$
(respectively,
$\xi \in E^{+}(v)$
(respectively,
 $\xi \in E^{-}(v)$
), the function
$\xi \in E^{-}(v)$
), the function
 $t \mapsto \|J_{\xi }(t)\|$
is non-increasing (respectively, non-decreasing).
$t \mapsto \|J_{\xi }(t)\|$
is non-increasing (respectively, non-decreasing).
When
![]() $\gamma _v(t)$
is a flat geodesic, there exists a non-trivial element
$\gamma _v(t)$
is a flat geodesic, there exists a non-trivial element
![]() $\xi \in E^+(v)\cap E^-(v)$
, and
$\xi \in E^+(v)\cap E^-(v)$
, and
![]() $J_{\xi }$
is a parallel Jacobi field along
$J_{\xi }$
is a parallel Jacobi field along
![]() $\gamma _v(t)$
, that is,
$\gamma _v(t)$
, that is,
![]() $J_{\xi }'(t)=0 \text { for all }\ t\in \mathbb {R}$
. In this case,
$J_{\xi }'(t)=0 \text { for all }\ t\in \mathbb {R}$
. In this case,
![]() $E^+(v)$
and
$E^+(v)$
and
![]() $E^-(v)$
do not span the whole second tangent space
$E^-(v)$
do not span the whole second tangent space
![]() $T_vSM$
. The distributions
$T_vSM$
. The distributions
![]() $E^s$
and
$E^s$
and
![]() $E^u$
on
$E^u$
on
![]() $SM$
are integrable and their integral manifolds form foliations
$SM$
are integrable and their integral manifolds form foliations
![]() $W^s$
and
$W^s$
and
![]() $W^u$
of
$W^u$
of
![]() $SM$
, respectively. These two foliations are both invariant under
$SM$
, respectively. These two foliations are both invariant under
![]() $g^t$
, known as the stable and unstable horocycle foliations.
$g^t$
, known as the stable and unstable horocycle foliations.
2.2 Universal cover
Let
![]() $\widetilde {M}$
be the universal Riemannian cover of M, that is, a simply connected complete Riemannian manifold for which
$\widetilde {M}$
be the universal Riemannian cover of M, that is, a simply connected complete Riemannian manifold for which
![]() $M=\widetilde {M}/\Gamma $
, where
$M=\widetilde {M}/\Gamma $
, where
![]() $\Gamma $
is a discrete subgroup of the group of isometries of
$\Gamma $
is a discrete subgroup of the group of isometries of
![]() $\widetilde {M}$
, isomorphic to
$\widetilde {M}$
, isomorphic to
![]() $\pi _1(M)$
. Recall that we assume M has no focal points. According to the Hadmard–Cartan theorem, for each two points on
$\pi _1(M)$
. Recall that we assume M has no focal points. According to the Hadmard–Cartan theorem, for each two points on
![]() $\widetilde {M}$
, there is a unique geodesic segment joining them. Therefore,
$\widetilde {M}$
, there is a unique geodesic segment joining them. Therefore,
![]() $\widetilde {M}$
can be identified with the open unit disk in the plane. The lifting of a geodesic
$\widetilde {M}$
can be identified with the open unit disk in the plane. The lifting of a geodesic
![]() $\gamma $
from M to
$\gamma $
from M to
![]() $\widetilde {M}$
is denoted by
$\widetilde {M}$
is denoted by
![]() $\widetilde {\gamma }$
. Two geodesics
$\widetilde {\gamma }$
. Two geodesics
![]() $\widetilde \gamma _1$
and
$\widetilde \gamma _1$
and
![]() $\widetilde \gamma _2$
are said to be asymptotes if
$\widetilde \gamma _2$
are said to be asymptotes if
![]() $d(\widetilde \gamma _1(t), \widetilde \gamma _2(t)) \leq C$
for some
$d(\widetilde \gamma _1(t), \widetilde \gamma _2(t)) \leq C$
for some
![]() $C>0$
and
$C>0$
and
![]() $\text {for all }\ t>0$
. It is easy to check that the asymptotes relation is an equivalence relation. Let
$\text {for all }\ t>0$
. It is easy to check that the asymptotes relation is an equivalence relation. Let
![]() $\widetilde {M}(\infty )$
be the set of all the equivalence classes, which can be identified with the boundary of the unit disk. Then the set
$\widetilde {M}(\infty )$
be the set of all the equivalence classes, which can be identified with the boundary of the unit disk. Then the set
can be identified with the closed unit disk in the plane. Denote by
![]() $\widetilde {\gamma }(+\infty )$
the asymptote class of the geodesic
$\widetilde {\gamma }(+\infty )$
the asymptote class of the geodesic
![]() $\widetilde {\gamma }$
, and by
$\widetilde {\gamma }$
, and by
![]() $\widetilde {\gamma }(-\infty )$
the one of the reversed geodesic of
$\widetilde {\gamma }(-\infty )$
the one of the reversed geodesic of
![]() $\widetilde {\gamma }$
. We use
$\widetilde {\gamma }$
. We use
![]() $\widetilde {W}^s$
and
$\widetilde {W}^s$
and
![]() $\widetilde {W}^u$
to denote the lifting of
$\widetilde {W}^u$
to denote the lifting of
![]() $W^s$
and
$W^s$
and
![]() $W^u$
to
$W^u$
to
![]() $S\widetilde {M}$
, respectively. It is obvious that if
$S\widetilde {M}$
, respectively. It is obvious that if
![]() $w \in \widetilde {W}^s(v)$
, then geodesics
$w \in \widetilde {W}^s(v)$
, then geodesics
![]() $\widetilde {\gamma }_v(t)$
and
$\widetilde {\gamma }_v(t)$
and
![]() $\widetilde {\gamma }_w(t)$
are asymptotic.
$\widetilde {\gamma }_w(t)$
are asymptotic.
An isometry
![]() $\alpha $
of
$\alpha $
of
![]() $\widetilde {M}$
is called axial if there exist a geodesic
$\widetilde {M}$
is called axial if there exist a geodesic
![]() $\widetilde {\gamma }$
on
$\widetilde {\gamma }$
on
![]() $\widetilde {M}$
and a
$\widetilde {M}$
and a
![]() $t_{1}>0$
such that for all
$t_{1}>0$
such that for all
![]() $t\in \mathbb {R}$
,
$t\in \mathbb {R}$
,
![]() $\alpha (\widetilde \gamma (t)) = \widetilde \gamma (t+t_{1})$
. The corresponding geodesic
$\alpha (\widetilde \gamma (t)) = \widetilde \gamma (t+t_{1})$
. The corresponding geodesic
![]() $\widetilde \gamma $
is called an axis of
$\widetilde \gamma $
is called an axis of
![]() $\alpha $
. The following result is due to Watkins [Reference Watkins24], which is proved for rank-
$\alpha $
. The following result is due to Watkins [Reference Watkins24], which is proved for rank-
![]() $1$
manifolds without focal points. Here we only need it for surfaces without focal points.
$1$
manifolds without focal points. Here we only need it for surfaces without focal points.
Lemma 2.3. (Cf. [Reference Watkins24, Theorem 6.11])
Let
![]() $\widetilde \gamma $
be an axis of an isometry
$\widetilde \gamma $
be an axis of an isometry
![]() $\alpha $
of
$\alpha $
of
![]() $\widetilde {M}$
. Suppose that
$\widetilde {M}$
. Suppose that
![]() $\widetilde \gamma $
is not the boundary of a flat half-plane. Then for all neighborhoods
$\widetilde \gamma $
is not the boundary of a flat half-plane. Then for all neighborhoods
![]() $U \subseteq \overline {M}$
of
$U \subseteq \overline {M}$
of
![]() $\widetilde \gamma (-\infty )$
and
$\widetilde \gamma (-\infty )$
and
![]() $V \subseteq \overline {M}$
of
$V \subseteq \overline {M}$
of
![]() $\widetilde \gamma (+\infty )$
, there is an integer
$\widetilde \gamma (+\infty )$
, there is an integer
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
for all
![]() $n \geq N$
.
$n \geq N$
.
Obviously, every closed geodesic
![]() $\gamma $
in M can be lifted to a geodesic
$\gamma $
in M can be lifted to a geodesic
![]() $\widetilde {\gamma }$
on
$\widetilde {\gamma }$
on
![]() $\widetilde {M}$
, such that
$\widetilde {M}$
, such that
for some
![]() $t_0>0$
and
$t_0>0$
and
![]() $\phi \in \pi _1(M)$
. Therefore,
$\phi \in \pi _1(M)$
. Therefore,
![]() $\widetilde \gamma $
is an axis of
$\widetilde \gamma $
is an axis of
![]() $\phi $
. In this case, we also say that
$\phi $
. In this case, we also say that
![]() $\phi $
fixes
$\phi $
fixes
![]() $\widetilde {\gamma }$
, written as
$\widetilde {\gamma }$
, written as
![]() $\phi (\widetilde {\gamma })=\widetilde {\gamma }$
. Here,
$\phi (\widetilde {\gamma })=\widetilde {\gamma }$
. Here,
![]() $\phi $
acts on
$\phi $
acts on
![]() $\widetilde {M}(\infty )$
in a natural way and fixes exactly the two points
$\widetilde {M}(\infty )$
in a natural way and fixes exactly the two points
![]() $\widetilde {\gamma }(\pm \infty )$
. Moreover, by Lemma 2.3, for any
$\widetilde {\gamma }(\pm \infty )$
. Moreover, by Lemma 2.3, for any
![]() $x\in \widetilde {M}(\infty )$
,
$x\in \widetilde {M}(\infty )$
,
![]() $x \neq \widetilde {\gamma }(\pm \infty )$
, we have
$x \neq \widetilde {\gamma }(\pm \infty )$
, we have
3 The regular set
This section is devoted to proving Theorem 1.4. The proof of Theorem 1.4 in the non-positive curvature case is given in [Reference Wu25, Lemma 1.1]. In fact, it is already well known in folklore that, after Pesin’s Theorem 1.3, all that remains for ergodicity of the geodesic flow is to show that
![]() $\Lambda $
has zero Liouville measure. Nevertheless, to prove Theorem 1.4 in the no focal points case, we need to use some geometric properties of the geodesic flow which we will present below.
$\Lambda $
has zero Liouville measure. Nevertheless, to prove Theorem 1.4 in the no focal points case, we need to use some geometric properties of the geodesic flow which we will present below.
For a given
![]() $\xi \in T_vSM$
, we always let
$\xi \in T_vSM$
, we always let
![]() $J_{\xi }(t)$
be the unique Jacobi field satisfying the Jacobi equation (1) under initial conditions
$J_{\xi }(t)$
be the unique Jacobi field satisfying the Jacobi equation (1) under initial conditions
 $$ \begin{align*}J_{\xi}(0)=d\pi_{v}\xi,\quad \frac{d}{dt}\bigg|_{t=0}J_{\xi}(t)=K_{v}\xi.\end{align*} $$
$$ \begin{align*}J_{\xi}(0)=d\pi_{v}\xi,\quad \frac{d}{dt}\bigg|_{t=0}J_{\xi}(t)=K_{v}\xi.\end{align*} $$
Suppose that
![]() $J_{\xi }(t)$
is perpendicular to
$J_{\xi }(t)$
is perpendicular to
![]() $\gamma ^{\prime }_v(t)$
, then
$\gamma ^{\prime }_v(t)$
, then
![]() $J_{\xi }(t)=j_{\xi }(t)e_2(t)$
and
$J_{\xi }(t)=j_{\xi }(t)e_2(t)$
and
![]() $j_{\xi }(t)=\|J_{\xi }(t)\|$
. Denote
$j_{\xi }(t)=\|J_{\xi }(t)\|$
. Denote
![]() $u_{\xi }(t)=j^{\prime }_{\xi }(t)/j_{\xi }(t)$
. Recall that
$u_{\xi }(t)=j^{\prime }_{\xi }(t)/j_{\xi }(t)$
. Recall that
![]() $u_{\xi }$
is a solution of the Riccati equation (3).
$u_{\xi }$
is a solution of the Riccati equation (3).
Given
![]() $\xi \in T_vSM$
, the Lyapunov exponent
$\xi \in T_vSM$
, the Lyapunov exponent
![]() $\chi (v, \xi )$
is defined as
$\chi (v, \xi )$
is defined as
The following proposition shows the connection between the Lyapunov exponent
![]() $\chi (v, \xi )$
and the function
$\chi (v, \xi )$
and the function
![]() $u_{\xi }$
.
$u_{\xi }$
.
Proposition 3.1. For any
![]() $v\in SM$
and
$v\in SM$
and
![]() $\xi \in E^+(v)$
, one has
$\xi \in E^+(v)$
, one has
 $$ \begin{align*}\chi(v, \xi)=\limsup_{T\to \infty}\frac{1}{T}\int_0^Tu_{\xi}(t)\,dt.\end{align*} $$
$$ \begin{align*}\chi(v, \xi)=\limsup_{T\to \infty}\frac{1}{T}\int_0^Tu_{\xi}(t)\,dt.\end{align*} $$
Proof. By the definition of Lyapunov exponents and Proposition 2.2(5), we have
 $$ \begin{align*} \chi(v, \xi)&=\limsup_{T\to \infty}\frac{1}{T}\log\|dg^T\xi\|=\limsup_{T\to \infty}\frac{1}{T}\log \sqrt{\|J_{\xi}(T)\|^2+\|J^{\prime}_{\xi}(T)\|^2}\\ &=\limsup_{T\to \infty}\frac{1}{T}\log \|J_{\xi}(T)\|=\limsup_{T\to \infty}\frac{1}{T}\int_0^T(\log j_{\xi}(t))'\,dt\\ &=\limsup_{T\to \infty}\frac{1}{T}\int_0^T\frac{j_{\xi}'(t)}{j_{\xi}(t)}dt=\limsup_{T\to \infty}\frac{1}{T}\int_0^Tu_{\xi}(t)\,dt.\\[-46pt] \end{align*} $$
$$ \begin{align*} \chi(v, \xi)&=\limsup_{T\to \infty}\frac{1}{T}\log\|dg^T\xi\|=\limsup_{T\to \infty}\frac{1}{T}\log \sqrt{\|J_{\xi}(T)\|^2+\|J^{\prime}_{\xi}(T)\|^2}\\ &=\limsup_{T\to \infty}\frac{1}{T}\log \|J_{\xi}(T)\|=\limsup_{T\to \infty}\frac{1}{T}\int_0^T(\log j_{\xi}(t))'\,dt\\ &=\limsup_{T\to \infty}\frac{1}{T}\int_0^T\frac{j_{\xi}'(t)}{j_{\xi}(t)}dt=\limsup_{T\to \infty}\frac{1}{T}\int_0^Tu_{\xi}(t)\,dt.\\[-46pt] \end{align*} $$
Throughout this section, if
![]() $\xi \in E^+(v)$
, we write
$\xi \in E^+(v)$
, we write
![]() $j(t):=j_{\xi }(t)$
and
$j(t):=j_{\xi }(t)$
and
![]() $u(t):=u_{\xi }(t)$
for simplicity. By Proposition 2.2(8) and the definition of
$u(t):=u_{\xi }(t)$
for simplicity. By Proposition 2.2(8) and the definition of
![]() $u(t)$
, we know that
$u(t)$
, we know that
![]() $u(t)\,{\leq}\, 0 \text{for all } t\in \mathbb {R}$
.
$u(t)\,{\leq}\, 0 \text{for all } t\in \mathbb {R}$
.
The following notion of uniformly recurrent vectors appeared in [Reference Ballmann, Brin and Eberlein4].
Definition 3.2. (Cf. [Reference Ballmann, Brin and Eberlein4])
A vector
![]() $x\in SM$
is said to be uniformly recurrent if for any neighborhood U of x in
$x\in SM$
is said to be uniformly recurrent if for any neighborhood U of x in
![]() $SM$
,
$SM$
,
 $$ \begin{align*}\liminf_{t \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_U(g^t(x))\,dt> 0,\end{align*} $$
$$ \begin{align*}\liminf_{t \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_U(g^t(x))\,dt> 0,\end{align*} $$
where
![]() $\mathbf {I}_U$
is the characteristic function of U.
$\mathbf {I}_U$
is the characteristic function of U.
The next lemma about the set of uniformly recurrent vectors was stated in [Reference Ballmann, Brin and Eberlein4] without a proof, so we provide a proof here. It will be used later in our proof of Theorem 1.4.
Lemma 3.3. Let
![]() $\Gamma $
be the set of all the uniformly recurrent vectors. Then
$\Gamma $
be the set of all the uniformly recurrent vectors. Then
![]() $\Gamma $
has full Liouville measure.
$\Gamma $
has full Liouville measure.
Proof. Let
![]() $\{U_n\}_{n\in \mathbb {N}}$
be a countable base consisting of open sets on
$\{U_n\}_{n\in \mathbb {N}}$
be a countable base consisting of open sets on
![]() $SM$
. By the Birkhoff ergodic theorem, there exists a set
$SM$
. By the Birkhoff ergodic theorem, there exists a set
![]() $X \subset SM$
of full measure such that for all
$X \subset SM$
of full measure such that for all
![]() $x \in X$
and all
$x \in X$
and all
![]() $n\in \mathbb {N}$
, the limit
$n\in \mathbb {N}$
, the limit
 $$ \begin{align*}f_n(x):=\lim_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_{U_n}(g^t(x))\,dt\end{align*} $$
$$ \begin{align*}f_n(x):=\lim_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_{U_n}(g^t(x))\,dt\end{align*} $$
exists and
Assume the contrary that
![]() $\nu (\Gamma ^c)>0$
. Then,
$\nu (\Gamma ^c)>0$
. Then,
![]() $\Gamma ^c \cap X$
is non-empty. For each
$\Gamma ^c \cap X$
is non-empty. For each
![]() $y \in \Gamma ^c \cap X$
, which is not uniformly recurrent, there exists a neighborhood U of y in
$y \in \Gamma ^c \cap X$
, which is not uniformly recurrent, there exists a neighborhood U of y in
![]() $SM$
such that
$SM$
such that
 $$ \begin{align*} \liminf_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_U(g^t(y))\,dt =0. \end{align*} $$
$$ \begin{align*} \liminf_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_U(g^t(y))\,dt =0. \end{align*} $$
Then there exists an
![]() $n(y)$
such that
$n(y)$
such that
![]() $U_{n(y)} \subset U$
and
$U_{n(y)} \subset U$
and
 $$ \begin{align} f_{n(y)}(y)=\lim_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_{U_n}(g^t(y))\,dt \leq \liminf_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_U(g^t(y))\,dt =0. \end{align} $$
$$ \begin{align} f_{n(y)}(y)=\lim_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_{U_n}(g^t(y))\,dt \leq \liminf_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_U(g^t(y))\,dt =0. \end{align} $$
Since there are only countably many
![]() $U_n$
, we can find some N such that
$U_n$
, we can find some N such that
![]() ${\nu (U_N \cap \Gamma ^c \!\cap X)\!>}0$
. By equation (5),
${\nu (U_N \cap \Gamma ^c \!\cap X)\!>}0$
. By equation (5),
![]() $f_N(y)=0$
for any
$f_N(y)=0$
for any
![]() $y \in U_N \cap \Gamma ^c\cap X$
.
$y \in U_N \cap \Gamma ^c\cap X$
.
However, the Birkhoff ergodic theorem implies that for almost every
![]() $y \in U_N \cap \Gamma ^c\cap X$
, one has
$y \in U_N \cap \Gamma ^c\cap X$
, one has
 $$ \begin{align*}g(y):=\lim_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_{(U_N \cap \Gamma^c\cap X)}(g^t(y))\,dt\end{align*} $$
$$ \begin{align*}g(y):=\lim_{T \to \infty} \frac{1}{T}\int_0^T \mathbf{I}_{(U_N \cap \Gamma^c\cap X)}(g^t(y))\,dt\end{align*} $$
exists with
However, by equation (5), we have
![]() $g(y) \leq f_N(y)=0$
for all
$g(y) \leq f_N(y)=0$
for all
![]() $y \in U_N \cap \Gamma ^c\cap X$
, which contradicts equation (6). This proves the lemma.
$y \in U_N \cap \Gamma ^c\cap X$
, which contradicts equation (6). This proves the lemma.
Given an open set
![]() $U\subset SM$
and a unit vector
$U\subset SM$
and a unit vector
![]() $w\in SM$
, we say that the orbit
$w\in SM$
, we say that the orbit
![]() $g^tw$
has positive frequency of return to U if
$g^tw$
has positive frequency of return to U if
![]() $\liminf _{t\to \infty }({T_U(t)}/{t})>0$
, where
$\liminf _{t\to \infty }({T_U(t)}/{t})>0$
, where
![]() $T_U(t)$
denotes the total length of the set
$T_U(t)$
denotes the total length of the set
Now we are ready to prove Theorem 1.4.
Proof of Theorem 1.4
Choose an arbitrary
![]() $v\in \Lambda ^c \cap \Delta ^c \cap \Gamma $
, where
$v\in \Lambda ^c \cap \Delta ^c \cap \Gamma $
, where
![]() $\Gamma $
denotes the set of uniformly recurrent vectors. Recall that
$\Gamma $
denotes the set of uniformly recurrent vectors. Recall that
![]() $\nu (\Gamma )=1$
by Lemma 3.3. Without loss of generality, we assume
$\nu (\Gamma )=1$
by Lemma 3.3. Without loss of generality, we assume
![]() $v\in (\Delta ^+)^c$
. We claim that
$v\in (\Delta ^+)^c$
. We claim that
![]() $K(\gamma _v(t))\geq 0 \text { for all } t \in \mathbb {R}$
.
$K(\gamma _v(t))\geq 0 \text { for all } t \in \mathbb {R}$
.
Assume the contrary that
![]() $K(\gamma _v(t_0))<0$
for some
$K(\gamma _v(t_0))<0$
for some
![]() $t_0>0$
. Since
$t_0>0$
. Since
![]() $K(\gamma _v(t_0))<0$
, we can choose two open neighborhoods
$K(\gamma _v(t_0))<0$
, we can choose two open neighborhoods
![]() $W_1 \supset W_2$
of
$W_1 \supset W_2$
of
![]() $g^{t_0}v$
, such that
$g^{t_0}v$
, such that
![]() $-\delta _2< K|_{\pi (W_1)}<-\delta _1<0$
and
$-\delta _2< K|_{\pi (W_1)}<-\delta _1<0$
and
![]() $\text {dist}(\partial W_1, \partial W_2)>\sigma $
for some
$\text {dist}(\partial W_1, \partial W_2)>\sigma $
for some
![]() $\delta _2>\delta _1>0$
and
$\delta _2>\delta _1>0$
and
![]() $\sigma>0$
.
$\sigma>0$
.
Choose an open neighborhood U of v which is small enough, such that for any
![]() $w\in U$
, one has
$w\in U$
, one has
![]() $g^{t_0}(w)\in W_2.$
Since
$g^{t_0}(w)\in W_2.$
Since
![]() $\liminf _{T\to \infty }({1}/{T})\int _0^T\mathbf {I}_U(g^tv)\,dt>0$
, we have
$\liminf _{T\to \infty }({1}/{T})\int _0^T\mathbf {I}_U(g^tv)\,dt>0$
, we have
 $$ \begin{align*}\liminf_{T\to \infty}\frac{1}{T}\int_{t_0}^{T+t_0}\mathbf{I}_{W_2}(g^tv)\,dt>0.\end{align*} $$
$$ \begin{align*}\liminf_{T\to \infty}\frac{1}{T}\int_{t_0}^{T+t_0}\mathbf{I}_{W_2}(g^tv)\,dt>0.\end{align*} $$
Then the orbit of v has positive frequency of return to
![]() $W_2$
, that is,
$W_2$
, that is,
 $$ \begin{align} \liminf_{T\to \infty}\frac{T_{W_2}(T)}{T}&=\liminf_{T\to \infty}\frac{1}{T+t_0}\int_{0}^{T+t_0}\mathbf{I}_{W_2}(g^tv)\,dt\nonumber\\ &=\liminf_{T\to \infty}\frac{T}{T+t_0}\cdot\frac{1}{T}\int_{t_0}^{T+t_0}\mathbf{I}_{W_2}(g^tv)\,dt>0. \end{align} $$
$$ \begin{align} \liminf_{T\to \infty}\frac{T_{W_2}(T)}{T}&=\liminf_{T\to \infty}\frac{1}{T+t_0}\int_{0}^{T+t_0}\mathbf{I}_{W_2}(g^tv)\,dt\nonumber\\ &=\liminf_{T\to \infty}\frac{T}{T+t_0}\cdot\frac{1}{T}\int_{t_0}^{T+t_0}\mathbf{I}_{W_2}(g^tv)\,dt>0. \end{align} $$
Lemma 3.4. There exists a constant
![]() $c>0$
such that if
$c>0$
such that if
![]() $g^tv\in W_2$
, then
$g^tv\in W_2$
, then
![]() $u(t)\leq -c$
for all
$u(t)\leq -c$
for all
![]() $t\geq 0$
.
$t\geq 0$
.
Proof of Lemma 3.4
We prove the lemma by contradiction. Assume this is not true. Then there exists a sequence of
![]() $t_i \geq 0$
with
$t_i \geq 0$
with
![]() $g^{t_i}v\in W_2$
, but
$g^{t_i}v\in W_2$
, but
![]() $u(t_i)\to 0$
as
$u(t_i)\to 0$
as
![]() $i\to \infty $
. There exist
$i\to \infty $
. There exist
![]() $s_{i,1}<t_i<s_{i,2}$
such that
$s_{i,1}<t_i<s_{i,2}$
such that
![]() $g^{s_{i,1}}v, g^{s_{i,2}}v\in \partial W_1$
and
$g^{s_{i,1}}v, g^{s_{i,2}}v\in \partial W_1$
and
![]() $g^tv\in W_1$
for any
$g^tv\in W_1$
for any
![]() $s_{i,1}<t<s_{i,2}$
. In fact,
$s_{i,1}<t<s_{i,2}$
. In fact,
![]() $s_{i,1}+\sigma < t_i < s_{i,2}-\sigma $
.
$s_{i,1}+\sigma < t_i < s_{i,2}-\sigma $
.
Recall the Riccati equation
![]() $u'(t)+u^2(t)+K(t)=0$
. If i is large enough, then
$u'(t)+u^2(t)+K(t)=0$
. If i is large enough, then
![]() $u'(t_i)=-u^2(t_i)-K(t_i)>\delta _1>0$
. We claim that
$u'(t_i)=-u^2(t_i)-K(t_i)>\delta _1>0$
. We claim that
![]() $u(t)$
is strictly increasing in the interval
$u(t)$
is strictly increasing in the interval
![]() $(t_i, s_{i,2})$
. Indeed, if not, there is a smallest number
$(t_i, s_{i,2})$
. Indeed, if not, there is a smallest number
![]() $s_i\in (t_i, s_{i,2})$
such that
$s_i\in (t_i, s_{i,2})$
such that
![]() $u'(s_i)=0$
. Then
$u'(s_i)=0$
. Then
![]() ${u(s_i)>u(t_i)}$
, since
${u(s_i)>u(t_i)}$
, since
![]() $u'(t)>0$
for all
$u'(t)>0$
for all
![]() $t\in (t_i, s_i)$
. Therefore,
$t\in (t_i, s_i)$
. Therefore,
![]() $u'(s_i)=-u^2(s_i)-K(s_i)>\delta _1>0$
, which is a contradiction.
$u'(s_i)=-u^2(s_i)-K(s_i)>\delta _1>0$
, which is a contradiction.
It follows that
![]() $u'(t)=-u^2(t)-K(t)>\delta _1>0$
for all
$u'(t)=-u^2(t)-K(t)>\delta _1>0$
for all
![]() $t\in (t_i, s_{i,2})$
. Thus,
$t\in (t_i, s_{i,2})$
. Thus,
 $$ \begin{align*} \begin{aligned} u(s_{i,2})&=u(t_i)+\int_{t_i}^{s_{i,2}}u'(t)\,dt\\ &>u(t_i)+\delta_1(s_{i,2}-t_i)>u(t_i)+\delta_1\sigma. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} u(s_{i,2})&=u(t_i)+\int_{t_i}^{s_{i,2}}u'(t)\,dt\\ &>u(t_i)+\delta_1(s_{i,2}-t_i)>u(t_i)+\delta_1\sigma. \end{aligned} \end{align*} $$
If i is large enough, then
![]() $u(t_i)$
is close enough to
$u(t_i)$
is close enough to
![]() $0$
, and hence
$0$
, and hence
![]() $u(s_{i,2})>0$
. This contradicts the fact that
$u(s_{i,2})>0$
. This contradicts the fact that
![]() $u(t)\leq 0 \text { for all } t\in \mathbb {R}$
.
$u(t)\leq 0 \text { for all } t\in \mathbb {R}$
.
Let us go on with the proof of Theorem 1.4. By Proposition 3.1, Lemma 3.4, and equation (7), one has
 $$ \begin{align*} \begin{aligned} \chi(v, \xi)=\limsup_{T\to \infty}\frac{1}{T}\int_0^Tu(t)\,dt\leq \limsup_{T\to \infty}\frac{1}{T}\cdot T_{W_2}(v)\cdot (-c)<0, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \chi(v, \xi)=\limsup_{T\to \infty}\frac{1}{T}\int_0^Tu(t)\,dt\leq \limsup_{T\to \infty}\frac{1}{T}\cdot T_{W_2}(v)\cdot (-c)<0, \end{aligned} \end{align*} $$
where
![]() $\xi \in E^+(v)$
. This contradicts
$\xi \in E^+(v)$
. This contradicts
![]() $v\in (\Delta ^+)^c$
. Thus,
$v\in (\Delta ^+)^c$
. Thus,
![]() $K(\gamma _v(t))\geq 0$
for all
$K(\gamma _v(t))\geq 0$
for all
![]() $t\geq 0$
. Analogously, we can prove that
$t\geq 0$
. Analogously, we can prove that
![]() $K(\gamma _v(t))\geq 0$
for all
$K(\gamma _v(t))\geq 0$
for all
![]() $t\leq 0$
. Thus,
$t\leq 0$
. Thus,
Now recall the Riccati equation
![]() $u'(t)+u^2(t)+K(t)=0$
again. Since
$u'(t)+u^2(t)+K(t)=0$
again. Since
![]() $K(t)\geq 0$
along
$K(t)\geq 0$
along
![]() $\gamma _v(t)$
, we have
$\gamma _v(t)$
, we have
![]() $u'(t)\leq 0$
for all
$u'(t)\leq 0$
for all
![]() $t\in \mathbb {R}$
. We have the following three possibilities.
$t\in \mathbb {R}$
. We have the following three possibilities.
-
(1)
 $\lim _{t\to \infty }u(t)=0$
. Since
$\lim _{t\to \infty }u(t)=0$
. Since
 $u(t)\leq 0$
and
$u(t)\leq 0$
and
 $u'(t)\leq 0$
for all
$u'(t)\leq 0$
for all
 $t\in \mathbb {R}$
, we must have
$t\in \mathbb {R}$
, we must have
 $u(t)\equiv ~0 \text { for all } t\in \mathbb {R}$
. Then
$u(t)\equiv ~0 \text { for all } t\in \mathbb {R}$
. Then
 $u'(t)\equiv 0 \text { for all } t\in \mathbb {R}$
. It follows from the Riccati equation that
$u'(t)\equiv 0 \text { for all } t\in \mathbb {R}$
. It follows from the Riccati equation that
 $K(t)\equiv 0 \text { for all } t\in \mathbb {R}$
.
$K(t)\equiv 0 \text { for all } t\in \mathbb {R}$
. -
(2)
 $\lim _{t\to \infty }u(t)=-d<0$
for some
$\lim _{t\to \infty }u(t)=-d<0$
for some
 $d>0$
. Then,
$d>0$
. Then,  $$ \begin{align*} u'(t)=-u^2(t)-K(t)\leq -u^2(t)<0 \quad \text{for all } t\in \mathbb{R}. \end{align*} $$
$$ \begin{align*} u'(t)=-u^2(t)-K(t)\leq -u^2(t)<0 \quad \text{for all } t\in \mathbb{R}. \end{align*} $$
This contradicts the fact that
 $\lim _{t\to \infty }u'(t)=0$
.
$\lim _{t\to \infty }u'(t)=0$
. -
(3)
 $\lim _{t\to \infty }u(t)=-\infty $
. Since
$\lim _{t\to \infty }u(t)=-\infty $
. Since
 $J(t)$
is a stable Jacobi field along
$J(t)$
is a stable Jacobi field along
 $\gamma _v(t)$
, we have
$\gamma _v(t)$
, we have
 $|u(t)|=|j'(t)/j(t)|\leq a$
. We also arrive at a contradiction.
$|u(t)|=|j'(t)/j(t)|\leq a$
. We also arrive at a contradiction.
In summary, we must have
![]() $K(\gamma _v(t))\equiv 0 \text { for all } t\in \mathbb {R}$
. This contradicts our assumption
$K(\gamma _v(t))\equiv 0 \text { for all } t\in \mathbb {R}$
. This contradicts our assumption
![]() $v\in \Lambda ^c$
. Therefore,
$v\in \Lambda ^c$
. Therefore,
![]() $\Lambda ^c\cap (\Delta ^+)^c\cap \Gamma =\emptyset $
. The case
$\Lambda ^c\cap (\Delta ^+)^c\cap \Gamma =\emptyset $
. The case
![]() $v\in (\Delta ^-)^c$
can be dealt with similarly and leads to the same result. Based on the discussion above, we can conclude that
$v\in (\Delta ^-)^c$
can be dealt with similarly and leads to the same result. Based on the discussion above, we can conclude that
![]() ${\Lambda ^c\cap \Delta ^c\cap \Gamma =\emptyset }$
. Since
${\Lambda ^c\cap \Delta ^c\cap \Gamma =\emptyset }$
. Since
![]() $\Gamma $
is a full measure set, we immediately know that
$\Gamma $
is a full measure set, we immediately know that
We are done with the proof of Theorem 1.4.
4 Flat geodesics
4.1 Flat strips are closed
A flat strip means a totally geodesic isometric imbedding
![]() $r:\mathbb {R}\times [0,c]\rightarrow \widetilde {M}$
, where
$r:\mathbb {R}\times [0,c]\rightarrow \widetilde {M}$
, where
![]() $\mathbb {R}\times [0,c]$
is a strip in a Euclidean plane. The projection of a flat strip from
$\mathbb {R}\times [0,c]$
is a strip in a Euclidean plane. The projection of a flat strip from
![]() $\widetilde M$
to M is also called a flat strip. We have the following flat strip lemma.
$\widetilde M$
to M is also called a flat strip. We have the following flat strip lemma.
Lemma 4.1. (Cf. [Reference O’Sullivan21])
If two distinct geodesics
![]() $\widetilde {\alpha }$
and
$\widetilde {\alpha }$
and
![]() $\widetilde {\beta }$
satisfy
$\widetilde {\beta }$
satisfy
![]() $d(\widetilde {\alpha }(t), \widetilde {\beta }(t))\leq C$
for some
$d(\widetilde {\alpha }(t), \widetilde {\beta }(t))\leq C$
for some
![]() $C>0$
and
$C>0$
and
![]() $\text {for all } t\in \mathbb {R}$
, then they are the boundary curves of a flat strip in
$\text {for all } t\in \mathbb {R}$
, then they are the boundary curves of a flat strip in
![]() $\widetilde {M}$
.
$\widetilde {M}$
.
The flat strip lemma for non-positively curved manifolds was established by Eberlein and O’Neill in [Reference Eberlein and O’Neill13]. The above flat strip lemma for manifolds without focal points is due to Green in dimension two [Reference Green14], and O’Sullivan in arbitrary dimensions [Reference O’Sullivan21]. The following lemma is also useful in our work.
Lemma 4.2. (Cf. [Reference Wu25, Lemma 3.6])
If
![]() $w' \in W^s(w)\subset SM$
and
$w' \in W^s(w)\subset SM$
and
then
![]() $\gamma _w(t)$
and
$\gamma _w(t)$
and
![]() $\gamma _{w'}(t)$
converge to the boundaries of a flat strip of width
$\gamma _{w'}(t)$
converge to the boundaries of a flat strip of width
![]() $\delta $
.
$\delta $
.
In view of Conjecture 1.1, our aim is to show that all flat geodesics are closed. An important progress was made by Cao and Xavier on the flat geodesics inside flat strips on manifolds of non-positive curvature, in an unpublished preprint [Reference Cao and Xavier9] (see also [Reference Coudène and Schapira11]). We state it in the following theorem.
Theorem 4.3. (Cf. [Reference Cao and Xavier9])
Let M be a smooth, connected, and closed surface with genus
![]() $\mathfrak {g} \geq 2$
. Suppose that M has non-positive curvature. Then any flat strip on M consists of closed geodesics in the same homotopy type.
$\mathfrak {g} \geq 2$
. Suppose that M has non-positive curvature. Then any flat strip on M consists of closed geodesics in the same homotopy type.
Based on the flat strip Lemma 4.1, we generalize the above result to the manifolds without focal points. We adapt the argument of Cao and Xavier to surfaces without focal points.
Theorem 4.4. Let M be a smooth, connected, and closed surface with genus
![]() $\mathfrak {g} \geq 2$
. Suppose that M has no focal points. Then any flat strip on M consists of closed geodesics in the same homotopy type.
$\mathfrak {g} \geq 2$
. Suppose that M has no focal points. Then any flat strip on M consists of closed geodesics in the same homotopy type.
Proof. Observe that in the universal cover
![]() $\widetilde {M}$
, there exists an upper bound for the width of all the flat strips. Indeed, let
$\widetilde {M}$
, there exists an upper bound for the width of all the flat strips. Indeed, let
![]() $D> \text {diam}(M)$
. Then a flat strip of width greater than
$D> \text {diam}(M)$
. Then a flat strip of width greater than
![]() $2D$
contains a fundamental domain in
$2D$
contains a fundamental domain in
![]() $\widetilde {M}$
. Hence, M must be a flat torus. This contradicts the fact that M has genus
$\widetilde {M}$
. Hence, M must be a flat torus. This contradicts the fact that M has genus
![]() $\mathfrak {g} \geq 2$
.
$\mathfrak {g} \geq 2$
.
Let
![]() $\widetilde {G}: (-\infty , \infty )\times [0, \epsilon _0]\to \widetilde {M}$
be a flat strip in
$\widetilde {G}: (-\infty , \infty )\times [0, \epsilon _0]\to \widetilde {M}$
be a flat strip in
![]() $\widetilde {M}$
and
$\widetilde {M}$
and
![]() $G=p(\widetilde {G})$
, where
$G=p(\widetilde {G})$
, where
![]() ${p: \widetilde {M}\to M}$
is the universal covering map. Consider a sequence of unit vectors
${p: \widetilde {M}\to M}$
is the universal covering map. Consider a sequence of unit vectors
![]() $v_i\in SM$
where
$v_i\in SM$
where
![]() $v_i={\partial G}/{\partial t}(i, \epsilon _0), i=1,2, \ldots. $
Since
$v_i={\partial G}/{\partial t}(i, \epsilon _0), i=1,2, \ldots. $
Since
![]() $SM$
is compact, there exists a subsequence of
$SM$
is compact, there exists a subsequence of
![]() $\{v_i\}_{i=1}^{\infty }$
which converges to a unit vector
$\{v_i\}_{i=1}^{\infty }$
which converges to a unit vector
![]() $v_0\in SM$
. For simplicity of notation, we still let
$v_0\in SM$
. For simplicity of notation, we still let
![]() $\{v_i\}_{i=1}^{\infty }$
denote the subsequence. Recall that
$\{v_i\}_{i=1}^{\infty }$
denote the subsequence. Recall that
![]() $\pi : SM \to M$
is the canonical projection. Let
$\pi : SM \to M$
is the canonical projection. Let
![]() $x_i$
denote the foot point of
$x_i$
denote the foot point of
![]() $v_i$
, that is,
$v_i$
, that is,
![]() $x_i=\pi (v_i),\, i=0,1,2, \ldots .$
$x_i=\pi (v_i),\, i=0,1,2, \ldots .$
Let
![]() $\delta $
be the injectivity radius of M. For sufficiently large j, we may assume
$\delta $
be the injectivity radius of M. For sufficiently large j, we may assume
![]() $d(v_j, v_0)<\delta /2$
. We choose a preimage
$d(v_j, v_0)<\delta /2$
. We choose a preimage
![]() $\widetilde {x}_0\in p^{-1}(x_0)$
such that
$\widetilde {x}_0\in p^{-1}(x_0)$
such that
![]() $\widetilde {x}_0$
is the nearest point to the flat strip
$\widetilde {x}_0$
is the nearest point to the flat strip
![]() $\widetilde {G}$
in
$\widetilde {G}$
in
![]() $p^{-1}(x_0)$
. Then
$p^{-1}(x_0)$
. Then
![]() $p|_{B(\widetilde {x}_0, \delta )}: B(\widetilde {x}_0, \delta ) \to B(x_0, \delta )$
and
$p|_{B(\widetilde {x}_0, \delta )}: B(\widetilde {x}_0, \delta ) \to B(x_0, \delta )$
and
![]() $\Psi :=dp|_{SB(\widetilde {x}_0, \delta )}: SB(\widetilde {x}_0, \delta ) \to SB(x_0, \delta )$
are both isometries.
$\Psi :=dp|_{SB(\widetilde {x}_0, \delta )}: SB(\widetilde {x}_0, \delta ) \to SB(x_0, \delta )$
are both isometries.
Denote
![]() $w_i=\Psi ^{-1}(v_i)\in SB(\widetilde {x}_0, \delta ),\ i=0,1,2, \ldots. $
Let
$w_i=\Psi ^{-1}(v_i)\in SB(\widetilde {x}_0, \delta ),\ i=0,1,2, \ldots. $
Let
![]() $F_j: (-\infty , \infty )\times [0, \epsilon _0]\to \widetilde {M}$
denote the lifted flat strip tangent to
$F_j: (-\infty , \infty )\times [0, \epsilon _0]\to \widetilde {M}$
denote the lifted flat strip tangent to
![]() $w_j,\ j=1,2, \ldots. $
Then the limit of
$w_j,\ j=1,2, \ldots. $
Then the limit of
![]() $F_j$
is a flat strip
$F_j$
is a flat strip
![]() $\widetilde {G}_0: (-\infty , \infty )\times [0, \epsilon _0]\to \widetilde {M}$
tangent to
$\widetilde {G}_0: (-\infty , \infty )\times [0, \epsilon _0]\to \widetilde {M}$
tangent to
![]() $w_0$
. There are two distinct cases.
$w_0$
. There are two distinct cases.
-
(1)
 $p\circ F_{j_0}$
is periodic for some
$p\circ F_{j_0}$
is periodic for some
 $j_0\in \mathbb {N}$
. As
$j_0\in \mathbb {N}$
. As
 $p\circ F_{j_0}$
is the flat strip tangent to
$p\circ F_{j_0}$
is the flat strip tangent to
 $v_{j_0}$
, it coincides with G. Hence, G is periodic.
$v_{j_0}$
, it coincides with G. Hence, G is periodic. -
(2)
 $p\circ F_{j}$
is not periodic for any
$p\circ F_{j}$
is not periodic for any
 $j\in \mathbb {N}$
. Then
$j\in \mathbb {N}$
. Then
 $F_j$
and
$F_j$
and
 $\widetilde {G}_0$
are a pair of transversal flat strips of the same width
$\widetilde {G}_0$
are a pair of transversal flat strips of the same width
 $\epsilon _0$
. Suppose that they intersect at
$\epsilon _0$
. Suppose that they intersect at
 $q_j$
with angle
$q_j$
with angle
 $\alpha _j$
, where
$\alpha _j$
, where
 $q_j\in \partial F_j\cap \widetilde {G}_0((-\infty , \infty )\times \{\epsilon _0\})$
,
$q_j\in \partial F_j\cap \widetilde {G}_0((-\infty , \infty )\times \{\epsilon _0\})$
,
 $j=1, 2, \ldots .$
Because
$j=1, 2, \ldots .$
Because
 $F_j\cup \widetilde {G}_0$
has curvature
$F_j\cup \widetilde {G}_0$
has curvature
 $0$
everywhere, we can construct a rectangle
$0$
everywhere, we can construct a rectangle
 $R_j=[0, L_j]\times (0, \epsilon _0/8]$
contained in the closure of
$R_j=[0, L_j]\times (0, \epsilon _0/8]$
contained in the closure of
 $F_j-\widetilde {G}_0$
such that:
$F_j-\widetilde {G}_0$
such that:-
• one side of
 $R_j$
,
$R_j$
,
 $[0, L_j]\times \{0\}$
is contained in the line
$[0, L_j]\times \{0\}$
is contained in the line
 $\widetilde {G}_0((-\infty , \infty )\times \{\epsilon _0\})$
;
$\widetilde {G}_0((-\infty , \infty )\times \{\epsilon _0\})$
; -
•
 $L_j \geq {\epsilon _0}/{16\sin \alpha _j}$
.
$L_j \geq {\epsilon _0}/{16\sin \alpha _j}$
.
Attaching
 $R_j$
to
$R_j$
to
 $\widetilde {G}_0$
, we obtain an isometric embedding
$\widetilde {G}_0$
, we obtain an isometric embedding
 $\widetilde {G}_0: [c_j, c_j+L_j]\times [0, {9\epsilon _0}/{8}]$
for some
$\widetilde {G}_0: [c_j, c_j+L_j]\times [0, {9\epsilon _0}/{8}]$
for some
 $c_j\in \mathbb {R}$
. Let
$c_j\in \mathbb {R}$
. Let
 $\widetilde {u}_j$
be the unit vector tangent to
$\widetilde {u}_j$
be the unit vector tangent to
 $\widetilde {G}_0([c_j, c_j+L_j]\times \{0\})$
at the point
$\widetilde {G}_0([c_j, c_j+L_j]\times \{0\})$
at the point
 $\widetilde {G}_0(c_j+L_j/2,0)$
. Write
$\widetilde {G}_0(c_j+L_j/2,0)$
. Write
 $u_j=dp(\widetilde {u}_j)$
and suppose that a subsequence of
$u_j=dp(\widetilde {u}_j)$
and suppose that a subsequence of
 $\{u_j\}$
converges to
$\{u_j\}$
converges to
 $u_0$
. As
$u_0$
. As
 $L_j \to \infty $
as
$L_j \to \infty $
as
 $j\to \infty $
, we know that there exists a flat strip tangent to
$j\to \infty $
, we know that there exists a flat strip tangent to
 $u_0$
of width
$u_0$
of width
 ${9\epsilon _0}/{8}$
. Hence, there exits a flat strip
${9\epsilon _0}/{8}$
. Hence, there exits a flat strip
 $\widetilde {G}_1$
of width
$\widetilde {G}_1$
of width
 ${9\epsilon _0}/{8}$
in
${9\epsilon _0}/{8}$
in
 $\widetilde {M}$
.
$\widetilde {M}$
. -
We are done if we arrive at the first case above. If we have the second case, we then repeat the argument for the new flat strip
![]() $\widetilde {G}_1$
. However, we cannot enlarge our flat strips by a factor
$\widetilde {G}_1$
. However, we cannot enlarge our flat strips by a factor
![]() $9/8$
again and again, as the width of the flat strips in
$9/8$
again and again, as the width of the flat strips in
![]() $\widetilde {M}$
have an upper bound
$\widetilde {M}$
have an upper bound
![]() $2D$
. Thus, we must arrive at the first case at some step. It follows that G is periodic.
$2D$
. Thus, we must arrive at the first case at some step. It follows that G is periodic.
4.2 Expansivity
The proof of Theorems 1.7 and 1.8 uses an argument based on the following expansivity property of a vector
![]() $x\in SM$
not tangent to a flat strip. This argument will be used later several times, in the proof of Theorems 1.7, 1.8, and Lemma 4.11.
$x\in SM$
not tangent to a flat strip. This argument will be used later several times, in the proof of Theorems 1.7, 1.8, and Lemma 4.11.
Definition 4.5. (Cf. [Reference Katok and Hasselblatt19, Definition 3.2.11])
We say
![]() $x\in SM$
has the expansivity property if there exists a small
$x\in SM$
has the expansivity property if there exists a small
![]() $\delta _0>0$
, such that whenever
$\delta _0>0$
, such that whenever
![]() $d(g^t(x), g^t(y))< \delta _0 \ \text {for all } t\in \mathbb {R}$
, then
$d(g^t(x), g^t(y))< \delta _0 \ \text {for all } t\in \mathbb {R}$
, then
![]() $y=g^{t_0}(x)$
for some
$y=g^{t_0}(x)$
for some
![]() $t_0$
with
$t_0$
with
![]() $|t_0|<\delta _0$
.
$|t_0|<\delta _0$
.
The flat strip lemma (Lemma 4.1) for surfaces without focal points guarantees the expansivity property for a unit vector which is not tangent to a flat strip.
Lemma 4.6. If
![]() $x\in SM$
is not tangent to a flat strip, then it has the expansivity property.
$x\in SM$
is not tangent to a flat strip, then it has the expansivity property.
Proof. We prove this lemma by contradiction. Assume the lemma does not hold. Then for an arbitrarily small
![]() $\epsilon>0$
less than the injectivity radius of M, there exists a point
$\epsilon>0$
less than the injectivity radius of M, there exists a point
![]() $y\in SM$
such that
$y\in SM$
such that
![]() $y\notin \mathcal {O} (x)$
and
$y\notin \mathcal {O} (x)$
and
![]() $d(\gamma _x(t), \gamma _y(t))< \epsilon \ \text {for all } t\in \mathbb {R}$
. By the choice of
$d(\gamma _x(t), \gamma _y(t))< \epsilon \ \text {for all } t\in \mathbb {R}$
. By the choice of
![]() $\epsilon $
, we can lift
$\epsilon $
, we can lift
![]() $\gamma _x(t)$
and
$\gamma _x(t)$
and
![]() $\gamma _y(t)$
to the universal cover
$\gamma _y(t)$
to the universal cover
![]() $\widetilde {M}$
such that
$\widetilde {M}$
such that
Thus, by the flat strip Lemma 4.1,
![]() $\widetilde {\gamma }_x(t)$
and
$\widetilde {\gamma }_x(t)$
and
![]() $\widetilde {\gamma }_y(t)$
bound a flat strip. Hence, x is tangent to a flat strip, which is a contradiction.
$\widetilde {\gamma }_y(t)$
bound a flat strip. Hence, x is tangent to a flat strip, which is a contradiction.
4.3 Area of ideal triangles
Given
![]() $x,y,z \in \widetilde {M}(\infty )$
, an ideal triangle with vertices
$x,y,z \in \widetilde {M}(\infty )$
, an ideal triangle with vertices
![]() $x, y, z$
means the region in
$x, y, z$
means the region in
![]() $\widetilde {M}$
bounded by the three geodesics joining the vertices. In the case when at least one of
$\widetilde {M}$
bounded by the three geodesics joining the vertices. In the case when at least one of
![]() $x, y, z$
is on
$x, y, z$
is on
![]() $\widetilde {M}(\infty )$
(the other points can be inside
$\widetilde {M}(\infty )$
(the other points can be inside
![]() $\widetilde {M}$
), we also call the region bounded by the three geodesics an ideal triangle. The following theorem about the ideal triangle is proved in [Reference Ruggiero23].
$\widetilde {M}$
), we also call the region bounded by the three geodesics an ideal triangle. The following theorem about the ideal triangle is proved in [Reference Ruggiero23].
The following theorem is a version of [Reference Ruggiero23, Theorem 1] for surfaces without focal points.
Theorem 4.7. Let M be a smooth, connected, and closed surface with genus
![]() $\mathfrak {g} \geq 2$
with no focal points. Suppose that
$\mathfrak {g} \geq 2$
with no focal points. Suppose that
![]() $\gamma $
is a flat geodesic which is asymptotic to a closed geodesic
$\gamma $
is a flat geodesic which is asymptotic to a closed geodesic
![]() $\beta $
. Then every ideal triangle having
$\beta $
. Then every ideal triangle having
![]() $\widetilde {\gamma }(t)$
as an edge has infinite area.
$\widetilde {\gamma }(t)$
as an edge has infinite area.
Proof. Suppose that
![]() $v=\widetilde {\gamma }'(0)$
, and
$v=\widetilde {\gamma }'(0)$
, and
![]() $c(s)\in S\widetilde M, s\in [0,a]$
is the curve in the stable horosphere
$c(s)\in S\widetilde M, s\in [0,a]$
is the curve in the stable horosphere
![]() $H^s(v)$
with
$H^s(v)$
with
![]() $c(0)=v$
. We want to show that the area of
$c(0)=v$
. We want to show that the area of
![]() $\pi g^{[0,\infty ]}c[0,a]$
is infinite. Assume the contrary. Then obviously,
$\pi g^{[0,\infty ]}c[0,a]$
is infinite. Assume the contrary. Then obviously,
where l denotes the length of the curve.
As in the remark after the proof of Proposition 3.1, we denote by
![]() $u(w), w\in S\widetilde M$
the function satisfying Riccati equation (3) with respect to stable Jacobi field
$u(w), w\in S\widetilde M$
the function satisfying Riccati equation (3) with respect to stable Jacobi field
![]() $J^s(w)$
. Then,
$J^s(w)$
. Then,
![]() $u(w)={\|J_w^s\|'}/{\|J^s_w\|}$
and
$u(w)={\|J_w^s\|'}/{\|J^s_w\|}$
and
![]() $u(w)\le 0$
. Given
$u(w)\le 0$
. Given
![]() $T>0$
, define
$T>0$
, define
 $$ \begin{align*} u_T(w):=\int_0^Tu(g^tw)\,dt. \end{align*} $$
$$ \begin{align*} u_T(w):=\int_0^Tu(g^tw)\,dt. \end{align*} $$
Note that u and hence
![]() $u_T$
are continuous functions. Since
$u_T$
are continuous functions. Since
![]() $\tilde \gamma $
is flat,
$\tilde \gamma $
is flat,
![]() $u(g^tv)=0 \text { for all } t\in \mathbb {R}$
. By continuity of u, for any
$u(g^tv)=0 \text { for all } t\in \mathbb {R}$
. By continuity of u, for any
![]() $s\in [0,a]$
,
$s\in [0,a]$
,
Then there exists large enough
![]() $T>0$
which depends on the unit vector
$T>0$
which depends on the unit vector
![]() $c(s)$
such that
$c(s)$
such that
By assumption,
![]() $\gamma $
is asymptotic to a closed geodesic
$\gamma $
is asymptotic to a closed geodesic
![]() $\beta $
. Without loss of generality, assume that
$\beta $
. Without loss of generality, assume that
![]() $\tilde \gamma (0)$
and
$\tilde \gamma (0)$
and
![]() $\tilde \beta (0)$
are close enough and
$\tilde \beta (0)$
are close enough and
![]() $v=\tilde \gamma '(0)$
is in the stable manifold of
$v=\tilde \gamma '(0)$
is in the stable manifold of
![]() $\tilde \beta '(0)$
. On compact manifold M,
$\tilde \beta '(0)$
. On compact manifold M,
![]() $\pi g^{[0,\infty ]}(c[0,a])$
is contained in a small compact neighborhood of the closed geodesic
$\pi g^{[0,\infty ]}(c[0,a])$
is contained in a small compact neighborhood of the closed geodesic
![]() $\beta $
. By the compactness and continuity, we can find a uniform constant
$\beta $
. By the compactness and continuity, we can find a uniform constant
![]() $T>0$
independent of
$T>0$
independent of
![]() $t\ge 0$
and
$t\ge 0$
and
![]() $s\in [0,a]$
such that
$s\in [0,a]$
such that
We introduce the following useful lemma. The proof is similar to that of [Reference Chen, Kao and Park10, Lemma 3.13].
Lemma 4.8. Let
![]() $\psi $
be a non-negative function and
$\psi $
be a non-negative function and
![]() $\psi _T(t):=\int _0^T \psi (t+\tau )\,d\tau $
. For
$\psi _T(t):=\int _0^T \psi (t+\tau )\,d\tau $
. For
![]() $a,b\in \mathbb {R}$
with
$a,b\in \mathbb {R}$
with
![]() $b-a\ge T$
, we have
$b-a\ge T$
, we have
 $$ \begin{align*}\frac{1}{T}\int_{a}^b\psi_T(t)\,dt \ge \int_{a+T}^b\psi(t)\,dt.\end{align*} $$
$$ \begin{align*}\frac{1}{T}\int_{a}^b\psi_T(t)\,dt \ge \int_{a+T}^b\psi(t)\,dt.\end{align*} $$
Note that
![]() $u\le 0$
in our case. Choose
$u\le 0$
in our case. Choose
![]() $L\ge T$
. Then by the above lemma, we have
$L\ge T$
. Then by the above lemma, we have
 $$ \begin{align} \frac{1}{T}\int_{-T}^{L}-u_{T}(g^tw)\,dt \ge \int_{0}^{L}-u(g^tw)\,dt \end{align} $$
$$ \begin{align} \frac{1}{T}\int_{-T}^{L}-u_{T}(g^tw)\,dt \ge \int_{0}^{L}-u(g^tw)\,dt \end{align} $$
for any
![]() $w\in S\widetilde M$
. We have
$w\in S\widetilde M$
. We have
 $$ \begin{align*} \begin{aligned} l(\pi g^{L+T}( c[a,b]))&=\int_0^a \|dg^{L+T}c(s)\|\,ds\\[4pt] &=\int_0^a \|J^s_{c(s)}(L+T)\|\,ds\\[4pt] &=\int_0^a (\pi g^Tc(s))'e^{\int_T^{L+T}u(g^tc(s))\,dt}ds. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} l(\pi g^{L+T}( c[a,b]))&=\int_0^a \|dg^{L+T}c(s)\|\,ds\\[4pt] &=\int_0^a \|J^s_{c(s)}(L+T)\|\,ds\\[4pt] &=\int_0^a (\pi g^Tc(s))'e^{\int_T^{L+T}u(g^tc(s))\,dt}ds. \end{aligned} \end{align*} $$
Given
![]() $s<t$
, denote by
$s<t$
, denote by
![]() $A_{s,t}$
the area of the region bounded by
$A_{s,t}$
the area of the region bounded by
![]() $\pi g^s(c[0,a])$
,
$\pi g^s(c[0,a])$
,
![]() $\pi g^t(c[0,a])$
,
$\pi g^t(c[0,a])$
,
![]() $\gamma $
and the geodesic tangent to
$\gamma $
and the geodesic tangent to
![]() $c(a)$
. Then by (10) and (9), we have
$c(a)$
. Then by (10) and (9), we have
 $$ \begin{align*} \begin{aligned} l(\pi g^{L+T}(c[a,b]))&\ge \int_0^a (\pi g^T c(s))'e^{{1}/{T}\int_{0}^{L+T}u_{T}(g^tc(s))\,dt}ds\\[6pt] &\ge \int_0^a (\pi g^T c(s))'e^{-\int_{0}^{L+T}l(g^tc(s))\,dt}ds\\[6pt] &= l(\pi g^{T}( c[a,b]))e^{-A_{0,L+T}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} l(\pi g^{L+T}(c[a,b]))&\ge \int_0^a (\pi g^T c(s))'e^{{1}/{T}\int_{0}^{L+T}u_{T}(g^tc(s))\,dt}ds\\[6pt] &\ge \int_0^a (\pi g^T c(s))'e^{-\int_{0}^{L+T}l(g^tc(s))\,dt}ds\\[6pt] &= l(\pi g^{T}( c[a,b]))e^{-A_{0,L+T}}. \end{aligned} \end{align*} $$
Similarly, we can prove
By induction, we have
Taking limit, since we are assuming
![]() $\lim _{n\to \infty }A_{0,nL+T}<\infty $
, we get
$\lim _{n\to \infty }A_{0,nL+T}<\infty $
, we get
This contradicts equation (8) and the theorem follows.
Remark 4.9. There is significant difference between the above proof and the proof in the non-positive curvature case by Ruggiero [Reference Ruggiero23]. In non-positive curvature, in the proof of Lemma 4.1 in [Reference Ruggiero23], we can have by Taylor’s formula
since the first derivative of the curvature function is zero at p. In the no focal points case, there could be positive curvature, and thus we may not have this formula. So the method using comparison theorem in [Reference Ruggiero23] breaks down here.
The idea using
![]() $({1}/{T})u_T$
instead of u in our method has appeared in [Reference Chen, Kao and Park10]. The assumption that the flat geodesic is asymptotic to a closed geodesic is used to get the uniform T in equation (9). However, we do not know a proof without this assumption.
$({1}/{T})u_T$
instead of u in our method has appeared in [Reference Chen, Kao and Park10]. The assumption that the flat geodesic is asymptotic to a closed geodesic is used to get the uniform T in equation (9). However, we do not know a proof without this assumption.
4.4 Non-closed flat geodesics
In this subsection, we discuss some important properties of the flat geodesics. Our Theorem 1.6 is a straightforward corollary of these properties. In fact, it is closely related to the following two lemmas (Lemmas 4.10 and 4.11). The first lemma shows that if a flat geodesic converges to a closed one (no matter flat or not), then the former geodesic must also be closed and coincide with the latter.
Lemma 4.10. Suppose that
![]() $y\in \Lambda $
and the
$y\in \Lambda $
and the
![]() $\omega $
-limit set
$\omega $
-limit set
![]() $\omega (y)= \mathcal {O}(z)$
, where
$\omega (y)= \mathcal {O}(z)$
, where
![]() $\mathcal {O}(z)$
is periodic. Then
$\mathcal {O}(z)$
is periodic. Then
![]() $\mathcal {O}(y)=\mathcal {O}(z)$
. In particular,
$\mathcal {O}(y)=\mathcal {O}(z)$
. In particular,
![]() $\mathcal {O}(y)$
is periodic.
$\mathcal {O}(y)$
is periodic.
Proof. Since
![]() $\omega (y)= \mathcal {O}(z)$
, we can lift geodesics
$\omega (y)= \mathcal {O}(z)$
, we can lift geodesics
![]() $\gamma _z(t), \gamma _y(t)$
to the universal cover
$\gamma _z(t), \gamma _y(t)$
to the universal cover
![]() $\widetilde {M}$
, denoted by
$\widetilde {M}$
, denoted by
![]() $\widetilde {\gamma }_0(t)$
and
$\widetilde {\gamma }_0(t)$
and
![]() $\widetilde {\gamma }(t)$
, respectively, such that
$\widetilde {\gamma }(t)$
, respectively, such that
![]() $\lim _{t\to +\infty }d(\widetilde {\gamma }_0(t), \widetilde {\gamma }(t))=0$
. In particular,
$\lim _{t\to +\infty }d(\widetilde {\gamma }_0(t), \widetilde {\gamma }(t))=0$
. In particular,
![]() $\widetilde {\gamma }_0(+\infty )=\widetilde {\gamma }(+\infty )$
.
$\widetilde {\gamma }_0(+\infty )=\widetilde {\gamma }(+\infty )$
.
Since
![]() $\gamma _z(t)$
is a closed geodesic, there exists an isometry
$\gamma _z(t)$
is a closed geodesic, there exists an isometry
![]() $\phi $
of
$\phi $
of
![]() $\widetilde {M}$
such that
$\widetilde {M}$
such that
![]() $\phi (\widetilde {\gamma }_0(t))=\widetilde {\gamma }_0(t+t_0)$
. Moreover, on the boundary of the disk
$\phi (\widetilde {\gamma }_0(t))=\widetilde {\gamma }_0(t+t_0)$
. Moreover, on the boundary of the disk
![]() $\widetilde {M}(\infty )$
,
$\widetilde {M}(\infty )$
,
![]() $\phi $
fixes exactly two points
$\phi $
fixes exactly two points
![]() $\widetilde {\gamma }_0(\pm \infty )$
, and for any other point
$\widetilde {\gamma }_0(\pm \infty )$
, and for any other point
![]() $a\in \widetilde {M}(\infty )$
,
$a\in \widetilde {M}(\infty )$
,
![]() $\lim _{n\to +\infty }\phi ^n(a)= \widetilde {\gamma }_0(+\infty )$
.
$\lim _{n\to +\infty }\phi ^n(a)= \widetilde {\gamma }_0(+\infty )$
.

Figure 1 Proof of Lemma 4.10.
Assume
![]() $\widetilde {\gamma }$
is not fixed by
$\widetilde {\gamma }$
is not fixed by
![]() $\phi $
. Then
$\phi $
. Then
![]() $\widetilde {\gamma }$
and
$\widetilde {\gamma }$
and
![]() $\phi (\widetilde {\gamma })$
do not intersect, since
$\phi (\widetilde {\gamma })$
do not intersect, since
![]() $\phi (\widetilde {\gamma })(+\infty )=\widetilde {\gamma }(+\infty )$
. By Lemma 2.3, replacing
$\phi (\widetilde {\gamma })(+\infty )=\widetilde {\gamma }(+\infty )$
. By Lemma 2.3, replacing
![]() $\phi $
by
$\phi $
by
![]() $\phi ^N$
for a large enough
$\phi ^N$
for a large enough
![]() $N\in \mathbb {N}$
if necessary, we know that the position of
$N\in \mathbb {N}$
if necessary, we know that the position of
![]() $\phi (\widetilde \gamma )$
must be as shown in Figure 1. We then pick another two geodesics
$\phi (\widetilde \gamma )$
must be as shown in Figure 1. We then pick another two geodesics
![]() $\widetilde {\alpha }$
and
$\widetilde {\alpha }$
and
![]() $\widetilde {\beta }$
as in Figure 1. The image of
$\widetilde {\beta }$
as in Figure 1. The image of
![]() $ABB'A'$
under
$ABB'A'$
under
![]() $\phi $
is
$\phi $
is
![]() $CEE'C'$
. Since
$CEE'C'$
. Since
![]() $\phi $
is an isometry, it preserves area. So the area of
$\phi $
is an isometry, it preserves area. So the area of
![]() $ABCD$
is equal to the region
$ABCD$
is equal to the region
![]() $A'B'DEE'C'$
, and thus greater than the area of the region
$A'B'DEE'C'$
, and thus greater than the area of the region
![]() $DEE'D'$
. We can let
$DEE'D'$
. We can let
![]() $A'$
and
$A'$
and
![]() $B'$
approach F. In this process, the area of the region
$B'$
approach F. In this process, the area of the region
![]() $DEE'D'$
approaches the area of the ideal triangle
$DEE'D'$
approaches the area of the ideal triangle
![]() $DEF$
. However, since
$DEF$
. However, since
![]() $\gamma _y$
is a flat geodesic asymptotic to a closed geodesic
$\gamma _y$
is a flat geodesic asymptotic to a closed geodesic
![]() $\gamma _z$
, the area of
$\gamma _z$
, the area of
![]() $DEF$
is infinite by Theorem 4.7. Then
$DEF$
is infinite by Theorem 4.7. Then
![]() $ABCD$
has infinite area which is absurd. So
$ABCD$
has infinite area which is absurd. So
![]() $\phi (\widetilde {\gamma })$
and
$\phi (\widetilde {\gamma })$
and
![]() $\widetilde {\gamma }$
must coincide.
$\widetilde {\gamma }$
must coincide.
Therefore,
![]() $\widetilde {\gamma }(\pm \infty )= \widetilde {\gamma }_0(\pm \infty )$
. Then either
$\widetilde {\gamma }(\pm \infty )= \widetilde {\gamma }_0(\pm \infty )$
. Then either
![]() $\widetilde {\gamma }(t)$
and
$\widetilde {\gamma }(t)$
and
![]() $\widetilde {\gamma }_0(t)$
bound a flat strip by the flat strip Lemma 4.1 or
$\widetilde {\gamma }_0(t)$
bound a flat strip by the flat strip Lemma 4.1 or
![]() $\widetilde {\gamma }(t)=\widetilde {\gamma }_0(t)$
. Recall that
$\widetilde {\gamma }(t)=\widetilde {\gamma }_0(t)$
. Recall that
![]() $\lim _{t\to +\infty }d(\widetilde {\gamma }(t), \widetilde {\gamma }_0(t))=0$
, we must have
$\lim _{t\to +\infty }d(\widetilde {\gamma }(t), \widetilde {\gamma }_0(t))=0$
, we must have
![]() $\widetilde {\gamma }(t)=\widetilde {\gamma }_0(t)$
. Hence,
$\widetilde {\gamma }(t)=\widetilde {\gamma }_0(t)$
. Hence,
![]() $\mathcal {O}(y)=\mathcal {O}(z)$
.
$\mathcal {O}(y)=\mathcal {O}(z)$
.
Lemma 4.10 can be strengthened to the following.
Lemma 4.11. Suppose that
![]() $y\in \Lambda $
and
$y\in \Lambda $
and
![]() $z\in \omega (y)$
, where z is periodic. Then
$z\in \omega (y)$
, where z is periodic. Then
![]() $\mathcal {O}(y)=\mathcal {O}(z)$
. In particular, y is periodic.
$\mathcal {O}(y)=\mathcal {O}(z)$
. In particular, y is periodic.
The proof of Lemma 4.11 follows from an argument similar to the one in the proof of [Reference Wu25, Lemma 3.8]. The argument relies on the expansivity property of a unit vector not tangent to a flat strip, as stated in Lemma 4.6. Then Theorem 1.6 follows from an almost identical argument. For this reason, we omit the proof here. Readers can check the proof of [Reference Wu25, Lemma 3.8, Theorem 1.5] for details of the argument.
5 Proof of main theorems
5.1 Proof of Theorem 1.8
Now we assume that
![]() $\Lambda \cap (\text {Per } (g^t))^c \neq \emptyset $
, in other words, there exists an aperiodic orbit
$\Lambda \cap (\text {Per } (g^t))^c \neq \emptyset $
, in other words, there exists an aperiodic orbit
![]() $\mathcal {O}(x)$
in
$\mathcal {O}(x)$
in
![]() $\Lambda $
. We will construct the points
$\Lambda $
. We will construct the points
![]() $y, z\in \Lambda $
as stated in Theorem 1.8 starting from
$y, z\in \Lambda $
as stated in Theorem 1.8 starting from
![]() $\mathcal {O}(x)$
based on the expansivity property of x. A first observation is that we can always find two arbitrarily nearby points on the orbit
$\mathcal {O}(x)$
based on the expansivity property of x. A first observation is that we can always find two arbitrarily nearby points on the orbit
![]() $\mathcal {O}(x)$
. We state this result in the following lemma (see [Reference Wu25, Lemma 3.3] for the proof).
$\mathcal {O}(x)$
. We state this result in the following lemma (see [Reference Wu25, Lemma 3.3] for the proof).
Lemma 5.1. For any
![]() $k\in \mathbb {N}$
, there exist two sequences
$k\in \mathbb {N}$
, there exist two sequences
![]() $t_k \to +\infty $
and
$t_k \to +\infty $
and
![]() $t^{\prime }_k\to +\infty $
, such that
$t^{\prime }_k\to +\infty $
, such that
![]() $t^{\prime }_k-t_k\to +\infty $
and
$t^{\prime }_k-t_k\to +\infty $
and
For each pair
![]() $x_k, x^{\prime }_k$
with large enough k, we can check the expansivity in the positive direction of the flow by using the idea in the proof of [Reference Wu25, Proposition 3.4]. In fact, the expansivity in one direction (either positive or negative) of the flow is sufficient for our purpose.
$x_k, x^{\prime }_k$
with large enough k, we can check the expansivity in the positive direction of the flow by using the idea in the proof of [Reference Wu25, Proposition 3.4]. In fact, the expansivity in one direction (either positive or negative) of the flow is sufficient for our purpose.
Proposition 5.2. Fix an arbitrarily small
![]() $\epsilon _0>0$
. Then there exists
$\epsilon _0>0$
. Then there exists
![]() $s_k\to +\infty $
or
$s_k\to +\infty $
or
![]() $s_k\to -\infty $
, such that
$s_k\to -\infty $
, such that
Proof. Assume the contrary. Then x does not have expansivity property. By Lemma 4.6, x is tangent to a flat strip. Then by Lemma 4.4, x must be periodic. This contradicts the assumption
![]() $x\in (\text {Per }(g^t))^c$
.
$x\in (\text {Per }(g^t))^c$
.
Without loss of generality, we suppose that
![]() $s_k \to +\infty $
in the remainder of the paper. For the case
$s_k \to +\infty $
in the remainder of the paper. For the case
![]() $s_k \to -\infty $
, everything remains true by a slight modification.
$s_k \to -\infty $
, everything remains true by a slight modification.
Proposition 5.3. There exist
![]() $\epsilon _0>0$
,
$\epsilon _0>0$
,
![]() $a, b\in \Lambda \cap (\text {Per }(g^t))^c$
such that
$a, b\in \Lambda \cap (\text {Per }(g^t))^c$
such that
Proof. We apply Proposition 5.2. Pick a subsequence
![]() $k_i\to +\infty $
such that both of the sequences
$k_i\to +\infty $
such that both of the sequences
![]() $\{g^{s_{k_i}}(x_{k_i})\}$
and
$\{g^{s_{k_i}}(x_{k_i})\}$
and
![]() $\{g^{s_{k_i}}(x^{\prime }_{k_i})\}$
converge. Let
$\{g^{s_{k_i}}(x^{\prime }_{k_i})\}$
converge. Let
Then
![]() $d(a, b)=\lim _{k_i\to +\infty }d(g^{s_{k_i}}(x_{k_i}),g^{s_{k_i}}(x^{\prime }_{k_i}))=\epsilon _0.$
We get equation (11).
$d(a, b)=\lim _{k_i\to +\infty }d(g^{s_{k_i}}(x_{k_i}),g^{s_{k_i}}(x^{\prime }_{k_i}))=\epsilon _0.$
We get equation (11).
For any
![]() $t<0$
, since
$t<0$
, since
![]() $0<s_{k_i}+t<s_{k_i}$
for some large
$0<s_{k_i}+t<s_{k_i}$
for some large
![]() $k_i$
, one has
$k_i$
, one has
Hence, we get equation (12).
Next assume that a is periodic. Since
then x is periodic by Lemma 4.11. This is a contradiction. So
![]() $a\in (\text {Per }(g^t))^c$
. Similarly,
$a\in (\text {Per }(g^t))^c$
. Similarly,
![]() $b\in (\text {Per }(g^t))^c$
. Thus,
$b\in (\text {Per }(g^t))^c$
. Thus,
![]() $a, b\in \Lambda \cap (\text {Per }(g^t))^c$
.
$a, b\in \Lambda \cap (\text {Per }(g^t))^c$
.
Now we prove equation (13), that is,
![]() $a \notin \mathcal {O}(b)$
. For a simpler notation, we write
$a \notin \mathcal {O}(b)$
. For a simpler notation, we write
The geodesics
![]() $\gamma _{x_k}(t), \gamma _{x^{\prime }_k}(t)$
on M can be lifted to
$\gamma _{x_k}(t), \gamma _{x^{\prime }_k}(t)$
on M can be lifted to
![]() $\widetilde {\gamma }_k, \widetilde {\gamma }^{\prime }_k$
on
$\widetilde {\gamma }_k, \widetilde {\gamma }^{\prime }_k$
on
![]() $\widetilde {M}$
in the way such that
$\widetilde {M}$
in the way such that
![]() $d(x_k, x^{\prime }_k)<{1}/{k}$
,
$d(x_k, x^{\prime }_k)<{1}/{k}$
,
![]() $d(y_k,y^{\prime }_k)=\epsilon _0$
, where
$d(y_k,y^{\prime }_k)=\epsilon _0$
, where
![]() $y_k=g^{s_k}(x_k)$
,
$y_k=g^{s_k}(x_k)$
,
![]() $y^{\prime }_k=g^{s_k}(x^{\prime }_k)$
, and moreover
$y^{\prime }_k=g^{s_k}(x^{\prime }_k)$
, and moreover
![]() ${y_k \to a}$
,
${y_k \to a}$
,
![]() $y^{\prime }_k \to b$
. Here we use a same notation for the lift of a point since no confusion is caused. Then
$y^{\prime }_k \to b$
. Here we use a same notation for the lift of a point since no confusion is caused. Then
![]() $\widetilde {\gamma }_k$
converges to
$\widetilde {\gamma }_k$
converges to
![]() $\widetilde {\gamma }=\widetilde {\gamma }_a$
,
$\widetilde {\gamma }=\widetilde {\gamma }_a$
,
![]() $\widetilde {\gamma }^{\prime }_k$
converges to
$\widetilde {\gamma }^{\prime }_k$
converges to
![]() $\widetilde {\gamma }'=\widetilde {\gamma }_b$
, and
$\widetilde {\gamma }'=\widetilde {\gamma }_b$
, and
![]() $d(a, b)= \epsilon _0$
. See Figure 2 (we use the same notation for a vector and its footpoint).
$d(a, b)= \epsilon _0$
. See Figure 2 (we use the same notation for a vector and its footpoint).

Figure 2 Proof of
![]() $\widetilde {\gamma } \neq \widetilde {\gamma }'$
.
$\widetilde {\gamma } \neq \widetilde {\gamma }'$
.
First we show that
![]() $d(y_k, \widetilde {\gamma }_k')$
is bounded away from
$d(y_k, \widetilde {\gamma }_k')$
is bounded away from
![]() $0$
. Write
$0$
. Write
![]() $d_k:= d(y_k, \widetilde {\gamma }^{\prime }_k)=d(y_k, z_k)$
,
$d_k:= d(y_k, \widetilde {\gamma }^{\prime }_k)=d(y_k, z_k)$
,
![]() $l_k:=d(y_k, x^{\prime }_k)$
,
$l_k:=d(y_k, x^{\prime }_k)$
,
![]() $b_k:= d(x^{\prime }_k, z_k)$
, and
$b_k:= d(x^{\prime }_k, z_k)$
, and
![]() $b^{\prime }_k:=d(z_k, y^{\prime }_k)$
. And we already know that
$b^{\prime }_k:=d(z_k, y^{\prime }_k)$
. And we already know that
![]() $d(x^{\prime }_k, y^{\prime }_k)=s_k$
. Suppose that
$d(x^{\prime }_k, y^{\prime }_k)=s_k$
. Suppose that
![]() $d_k \to 0$
as
$d_k \to 0$
as
![]() $k\to +\infty $
. By the triangle inequality,
$k\to +\infty $
. By the triangle inequality,
![]() $\lim _{k\to +\infty }(l_k-b_k)=0$
. Since
$\lim _{k\to +\infty }(l_k-b_k)=0$
. Since
![]() $\lim _{k\to +\infty }(l_k-s_k) \leq \lim _{k \to +\infty }d(x_k, x^{\prime }_k)=0$
, we have that
$\lim _{k\to +\infty }(l_k-s_k) \leq \lim _{k \to +\infty }d(x_k, x^{\prime }_k)=0$
, we have that
![]() $\lim _{k\to +\infty }b^{\prime }_k=\lim _{k\to +\infty }|(l_k-b_k)-(l_k-s_k)|=0$
. However, the triangle inequality implies
$\lim _{k\to +\infty }b^{\prime }_k=\lim _{k\to +\infty }|(l_k-b_k)-(l_k-s_k)|=0$
. However, the triangle inequality implies
![]() $\epsilon _0 \leq d_k+b_k' \to 0 $
, which is a contradiction. Now
$\epsilon _0 \leq d_k+b_k' \to 0 $
, which is a contradiction. Now
![]() $\widetilde {\gamma } \neq \widetilde {\gamma }'$
follows from
$\widetilde {\gamma } \neq \widetilde {\gamma }'$
follows from
![]() $d(a, \widetilde {\gamma }')=\lim _{k\to +\infty }d(y_k, \widetilde {\gamma }^{\prime }_k) \geq d_0$
for some
$d(a, \widetilde {\gamma }')=\lim _{k\to +\infty }d(y_k, \widetilde {\gamma }^{\prime }_k) \geq d_0$
for some
![]() $d_0>0$
.
$d_0>0$
.
Next we suppose there exists a deck transformation
![]() $\phi $
such that
$\phi $
such that
![]() $\phi (\widetilde {\gamma })=\widetilde {\gamma }'$
. See Figure 3. Observe that
$\phi (\widetilde {\gamma })=\widetilde {\gamma }'$
. See Figure 3. Observe that
![]() $\widetilde {\gamma }(-\infty )=\widetilde {\gamma }'(-\infty )$
since
$\widetilde {\gamma }(-\infty )=\widetilde {\gamma }'(-\infty )$
since
![]() $d(g^t(a), g^t(b))\leq \epsilon _0 \ \text {for all } t<0$
. Let
$d(g^t(a), g^t(b))\leq \epsilon _0 \ \text {for all } t<0$
. Let
![]() $\widetilde {\gamma }_0$
be the closed geodesic such that
$\widetilde {\gamma }_0$
be the closed geodesic such that
![]() $\phi (\widetilde {\gamma }_0)=\widetilde {\gamma }_0$
. Then
$\phi (\widetilde {\gamma }_0)=\widetilde {\gamma }_0$
. Then
![]() $\widetilde {\gamma }(-\infty )=\widetilde {\gamma }_0(-\infty )$
. By Lemma 4.11,
$\widetilde {\gamma }(-\infty )=\widetilde {\gamma }_0(-\infty )$
. By Lemma 4.11,
![]() $\widetilde {\gamma }$
is a closed geodesic, that is, a is a periodic point. We arrive at a contradiction. Hence, for any deck transformation
$\widetilde {\gamma }$
is a closed geodesic, that is, a is a periodic point. We arrive at a contradiction. Hence, for any deck transformation
![]() $\phi $
,
$\phi $
,
![]() $\phi (\widetilde {\gamma })\neq \widetilde {\gamma }'$
. So
$\phi (\widetilde {\gamma })\neq \widetilde {\gamma }'$
. So
![]() $a \notin \mathcal {O}(b)$
and we get equation (13).
$a \notin \mathcal {O}(b)$
and we get equation (13).

Figure 3 Proof of
![]() $\phi (\widetilde {\gamma }) \neq \widetilde {\gamma }'$
.
$\phi (\widetilde {\gamma }) \neq \widetilde {\gamma }'$
.
At last, if
![]() $a \notin W^u(b)$
, we can replace a by some
$a \notin W^u(b)$
, we can replace a by some
![]() $a' \in \mathcal {O}(a)$
, b by some
$a' \in \mathcal {O}(a)$
, b by some
![]() $b' \in \mathcal {O}(b)$
such that
$b' \in \mathcal {O}(b)$
such that
![]() $a'\in W^u(b')$
, and the above three properties still hold for a different
$a'\in W^u(b')$
, and the above three properties still hold for a different
![]() $\epsilon _0$
. We get equation (14).
$\epsilon _0$
. We get equation (14).
Proof of Theorem 1.8
We apply Proposition 5.3. Let
![]() $y=-a$
,
$y=-a$
,
![]() $z=-b$
. Then
$z=-b$
. Then
![]() $y, z \in \Lambda \cap (\text {Per }(g^t))^c$
,
$y, z \in \Lambda \cap (\text {Per }(g^t))^c$
,
![]() $d(g^t(y), g^t(z))\leq \epsilon _0\text { for all } t>0$
,
$d(g^t(y), g^t(z))\leq \epsilon _0\text { for all } t>0$
,
![]() $z \notin \mathcal {O}(y)$
and
$z \notin \mathcal {O}(y)$
and
![]() $y \in W^s(z)$
.
$y \in W^s(z)$
.
If
![]() $\epsilon _0$
is small enough, we can lift geodesics
$\epsilon _0$
is small enough, we can lift geodesics
![]() $\gamma _y(t)$
and
$\gamma _y(t)$
and
![]() $\gamma _z(t)$
to
$\gamma _z(t)$
to
![]() $\widetilde {\gamma }_y(t)$
and
$\widetilde {\gamma }_y(t)$
and
![]() $\widetilde {\gamma }_z(t)$
, respectively, on
$\widetilde {\gamma }_z(t)$
, respectively, on
![]() $\widetilde {M}$
, such that
$\widetilde {M}$
, such that
![]() $d(\widetilde {\gamma }_y(t),\widetilde {\gamma }_z(t)) \leq \epsilon _0$
for any
$d(\widetilde {\gamma }_y(t),\widetilde {\gamma }_z(t)) \leq \epsilon _0$
for any
![]() $t>0$
and
$t>0$
and
![]() $y\in \widetilde {W}^s(z)$
. Suppose
$y\in \widetilde {W}^s(z)$
. Suppose
![]() $\lim _{t\to +\infty } d(\widetilde {\gamma }_y(t), \widetilde {\gamma }_z(t))=\delta>0$
. Then by Lemma 4.2,
$\lim _{t\to +\infty } d(\widetilde {\gamma }_y(t), \widetilde {\gamma }_z(t))=\delta>0$
. Then by Lemma 4.2,
![]() $\widetilde {\gamma }_y(t)$
and
$\widetilde {\gamma }_y(t)$
and
![]() $\widetilde {\gamma }_z(t)$
converge to the boundary of a flat strip. Hence, y and z are periodic by Lemma 4.11, which is a contradiction. So we have
$\widetilde {\gamma }_z(t)$
converge to the boundary of a flat strip. Hence, y and z are periodic by Lemma 4.11, which is a contradiction. So we have
![]() $\lim _{t\to +\infty } d(\widetilde {\gamma }_y(t), \widetilde {\gamma }_z(t))=0$
. Hence,
$\lim _{t\to +\infty } d(\widetilde {\gamma }_y(t), \widetilde {\gamma }_z(t))=0$
. Hence,
5.2 Proof of Theorem 1.7
In the proof of Theorem 1.7, an argument similar to the one in Proposition 5.3 will be used.
Proof of Theorem 1.7
Suppose that
![]() $\Lambda \subset \text {Per }(g^t)$
. We will prove that if
$\Lambda \subset \text {Per }(g^t)$
. We will prove that if
![]() $x\in \Lambda $
, then x is tangent to an isolated closed flat geodesic or to a flat strip.
$x\in \Lambda $
, then x is tangent to an isolated closed flat geodesic or to a flat strip.
Assume the contrary to Theorem 1.7. Then there exists a sequence of different vectors
![]() $x^{\prime }_k \in \Lambda $
such that
$x^{\prime }_k \in \Lambda $
such that
![]() $\lim _{k\to +\infty }x^{\prime }_k=x$
for some
$\lim _{k\to +\infty }x^{\prime }_k=x$
for some
![]() $x\in \Lambda $
. Here, different
$x\in \Lambda $
. Here, different
![]() $x^{\prime }_k$
are tangent to different closed geodesics or to different flat strips, and x is tangent to a closed geodesic or to a flat strip. For large enough k, we suppose that
$x^{\prime }_k$
are tangent to different closed geodesics or to different flat strips, and x is tangent to a closed geodesic or to a flat strip. For large enough k, we suppose that
![]() $d(x^{\prime }_k, x) <{1}/{k}$
. Fix a small number
$d(x^{\prime }_k, x) <{1}/{k}$
. Fix a small number
![]() $\epsilon _0>0$
. It is impossible that
$\epsilon _0>0$
. It is impossible that
![]() $d(g^t(x^{\prime }_k), g^t(x)) \leq \epsilon _0 \ \text { for all } t>0$
. For otherwise,
$d(g^t(x^{\prime }_k), g^t(x)) \leq \epsilon _0 \ \text { for all } t>0$
. For otherwise,
![]() $\widetilde {\gamma }_{x^{\prime }_k}(t)$
and
$\widetilde {\gamma }_{x^{\prime }_k}(t)$
and
![]() $\widetilde {\gamma }_x(t)$
are positively asymptotic closed geodesics. They must be tangent to a common flat strip by Lemmas 4.2 and 4.10. This is impossible since different
$\widetilde {\gamma }_x(t)$
are positively asymptotic closed geodesics. They must be tangent to a common flat strip by Lemmas 4.2 and 4.10. This is impossible since different
![]() $x^{\prime }_k$
are tangent to different closed geodesics or to different flat strips. Hence, there exists a sequence
$x^{\prime }_k$
are tangent to different closed geodesics or to different flat strips. Hence, there exists a sequence
![]() $s_k\to +\infty $
such that
$s_k\to +\infty $
such that
and
Let
![]() $y_k:=g^{s_k}(x)$
and
$y_k:=g^{s_k}(x)$
and
![]() $y^{\prime }_k:=g^{s_k}(x^{\prime }_k)$
. Without loss of generality, we suppose that
$y^{\prime }_k:=g^{s_k}(x^{\prime }_k)$
. Without loss of generality, we suppose that
![]() $y_k\to a$
and
$y_k\to a$
and
![]() $y^{\prime }_k\to b$
. A similar proof as in Proposition 5.3 shows that
$y^{\prime }_k\to b$
. A similar proof as in Proposition 5.3 shows that
![]() $d(a, b)=\epsilon _0$
and
$d(a, b)=\epsilon _0$
and
![]() $d(g^t(a), g^t(b)) \leq \epsilon _0 \ \text {for all } t\leq 0$
. Replacing
$d(g^t(a), g^t(b)) \leq \epsilon _0 \ \text {for all } t\leq 0$
. Replacing
![]() $x, x_k'$
by
$x, x_k'$
by
![]() $-x, -x_k'$
, respectively, and applying the same argument, we can obtain two points
$-x, -x_k'$
, respectively, and applying the same argument, we can obtain two points
![]() $a^-,b^-$
such that
$a^-,b^-$
such that
![]() $d(a^-, b^-)=\epsilon _0$
and
$d(a^-, b^-)=\epsilon _0$
and
![]() $d(g^t(a^-), g^t(b^-)) \leq \epsilon _0 \ \text {for all } t\leq 0$
. Then we have the following three cases.
$d(g^t(a^-), g^t(b^-)) \leq \epsilon _0 \ \text {for all } t\leq 0$
. Then we have the following three cases.
-
(1)
 $\lim _{t\to \infty }d(g^t(-a), g^t(-b))=0$
. By Lemma 4.10,
$\lim _{t\to \infty }d(g^t(-a), g^t(-b))=0$
. By Lemma 4.10,
 $-a=-b$
. This contradicts
$-a=-b$
. This contradicts
 $d(a,b)=\epsilon _0$
.
$d(a,b)=\epsilon _0$
. -
(2)
 $\lim _{t\to \infty }d(g^t(-a^-), g^t(-b^-))=0$
. Also by Lemma 4.10,
$\lim _{t\to \infty }d(g^t(-a^-), g^t(-b^-))=0$
. Also by Lemma 4.10,
 $-a^-=-b^-$
. This contradicts
$-a^-=-b^-$
. This contradicts
 $d(a^-,b^-)=\epsilon _0$
.
$d(a^-,b^-)=\epsilon _0$
. -
(3)
 $\lim _{t\to \infty }d(g^t(-a), g^t(-b))>0$
and
$\lim _{t\to \infty }d(g^t(-a), g^t(-b))>0$
and
 $\lim _{t\to \infty }d(g^t(-a^-), g^t(-b^-))>0$
.
$\lim _{t\to \infty }d(g^t(-a^-), g^t(-b^-))>0$
.
For case (3), by Lemmas 4.2 and 4.11,
![]() $\gamma _{a}$
and
$\gamma _{a}$
and
![]() $\gamma _{x}$
coincide. And moreover,
$\gamma _{x}$
coincide. And moreover,
![]() $\gamma _{x}$
and
$\gamma _{x}$
and
![]() $\gamma _b$
are boundaries of a flat strip of width
$\gamma _b$
are boundaries of a flat strip of width
![]() $\delta _1>0$
. Similarly,
$\delta _1>0$
. Similarly,
![]() $\gamma _{x}$
and
$\gamma _{x}$
and
![]() $\gamma _{b^-}$
are boundaries of a flat strip of width
$\gamma _{b^-}$
are boundaries of a flat strip of width
![]() $\delta _2>0$
. We claim that these two flat strips lie on different sides of
$\delta _2>0$
. We claim that these two flat strips lie on different sides of
![]() $\gamma _x$
. Indeed, we choose
$\gamma _x$
. Indeed, we choose
![]() $\epsilon _0$
small enough and consider the
$\epsilon _0$
small enough and consider the
![]() $\epsilon _0$
-neighborhood of the closed geodesic
$\epsilon _0$
-neighborhood of the closed geodesic
![]() $\gamma _x$
which contains two regions lying on different sides of
$\gamma _x$
which contains two regions lying on different sides of
![]() $\gamma _x$
. By the definition of b and
$\gamma _x$
. By the definition of b and
![]() $b^-$
, they must lie in different regions as above. This implies the claim.
$b^-$
, they must lie in different regions as above. This implies the claim.
In this way, we get a flat strip of width
![]() $\delta _1+\delta _2$
and x is tangent to the interior of this flat strip. Since
$\delta _1+\delta _2$
and x is tangent to the interior of this flat strip. Since
![]() $g^{s_k}(x^{\prime }_k)\to b$
, we can repeat all the arguments above to
$g^{s_k}(x^{\prime }_k)\to b$
, we can repeat all the arguments above to
![]() $b, g^{s_k}(x^{\prime }_k)$
instead of
$b, g^{s_k}(x^{\prime }_k)$
instead of
![]() $x, x_k'$
. Then either we are arriving at a contradiction as in case (1) or case (2) and we are done, or we get a flat strip of width greater than
$x, x_k'$
. Then either we are arriving at a contradiction as in case (1) or case (2) and we are done, or we get a flat strip of width greater than
![]() $\delta _1+\delta _2$
and b is tangent to the interior of the flat strip. However, we can not enlarge a flat strip repeatedly in this way on a compact surface M. So we are done with the proof.
$\delta _1+\delta _2$
and b is tangent to the interior of the flat strip. However, we can not enlarge a flat strip repeatedly in this way on a compact surface M. So we are done with the proof.
5.3 Proof of Theorem 1.9
We shall prove Theorem 1.9 by showing that the second one of the dichotomy cannot happen if
![]() $\{p\in M: K(p)<0\}$
has at most finitely many connected components. The proof is an adaption of the one of [Reference Wu25, Theorem 1.6] to surfaces without focal points. Moreover, we fix a gap in that proof, which was pointed out by Keith Burns.
$\{p\in M: K(p)<0\}$
has at most finitely many connected components. The proof is an adaption of the one of [Reference Wu25, Theorem 1.6] to surfaces without focal points. Moreover, we fix a gap in that proof, which was pointed out by Keith Burns.
Proof of Theorem 1.9
Suppose
![]() $\Lambda \cap (\text {Per }(g^t))^c \neq \emptyset $
. Consider the two points y and z given by Theorem 1.8. We lift the geodesics
$\Lambda \cap (\text {Per }(g^t))^c \neq \emptyset $
. Consider the two points y and z given by Theorem 1.8. We lift the geodesics
![]() $\gamma _y(t)$
and
$\gamma _y(t)$
and
![]() $\gamma _z(t)$
to the geodesics in the universal cover
$\gamma _z(t)$
to the geodesics in the universal cover
![]() $\widetilde {M}$
, which are denoted by
$\widetilde {M}$
, which are denoted by
![]() $\widetilde {\gamma }_1$
and
$\widetilde {\gamma }_1$
and
![]() $\widetilde {\gamma }_2$
, respectively. See Figure 4.
$\widetilde {\gamma }_2$
, respectively. See Figure 4.

Figure 4 Proof of Theorem 1.9.
Consider the connected components of
![]() $\{p\in \widetilde {M}: K(p)<0\}$
on
$\{p\in \widetilde {M}: K(p)<0\}$
on
![]() $\widetilde {M}$
and we want to see how they distribute inside the ideal triangle bounded by
$\widetilde {M}$
and we want to see how they distribute inside the ideal triangle bounded by
![]() $\widetilde {\gamma }_1$
and
$\widetilde {\gamma }_1$
and
![]() $\widetilde {\gamma }_2$
. Since
$\widetilde {\gamma }_2$
. Since
![]() $\widetilde {\gamma }_1$
and
$\widetilde {\gamma }_1$
and
![]() $\widetilde {\gamma }_2$
are flat geodesics, no connected component intersects
$\widetilde {\gamma }_2$
are flat geodesics, no connected component intersects
![]() $\widetilde {\gamma }_1$
or
$\widetilde {\gamma }_1$
or
![]() $\widetilde {\gamma }_2$
. Note that such connected component may be not simply one lifting of (hence, not isometric to) one connected component of
$\widetilde {\gamma }_2$
. Note that such connected component may be not simply one lifting of (hence, not isometric to) one connected component of
![]() $\{p\in M: K(p)<0\}$
on the base space M. However, each of them projects onto a connected component on M.
$\{p\in M: K(p)<0\}$
on the base space M. However, each of them projects onto a connected component on M.
We claim that the maximal radius of inscribed disks inside each connected component is bounded away from
![]() $0$
. Indeed, if this is not true, then there exists an isometry between the inscribed disk with very small radius inside a connected component and an inscribed disk inside a connected component of
$0$
. Indeed, if this is not true, then there exists an isometry between the inscribed disk with very small radius inside a connected component and an inscribed disk inside a connected component of
![]() $\{p\in M: K(p)<0\}$
. This is impossible because the number of connected components of
$\{p\in M: K(p)<0\}$
. This is impossible because the number of connected components of
![]() $\{p\in M: K(p)<0\}$
is finite, and therefore the maximal radius of their inscribed disks is bounded away from
$\{p\in M: K(p)<0\}$
is finite, and therefore the maximal radius of their inscribed disks is bounded away from
![]() $0$
. The claim follows.
$0$
. The claim follows.
Let T denote the ideal triangle
![]() $\widetilde {\gamma }_1(0)\widetilde {\gamma }_2(0)w$
. We claim that a connected component of
$\widetilde {\gamma }_1(0)\widetilde {\gamma }_2(0)w$
. We claim that a connected component of
![]() $\{p\in \widetilde {M}: K(p)<0\}$
is bounded inside T, that is, it cannot approach w. Assume the contrary. Let D be a fundamental domain inside the ideal triangle bounded by
$\{p\in \widetilde {M}: K(p)<0\}$
is bounded inside T, that is, it cannot approach w. Assume the contrary. Let D be a fundamental domain inside the ideal triangle bounded by
![]() $\widetilde {\gamma }_1$
and
$\widetilde {\gamma }_1$
and
![]() $\widetilde {\gamma }_2$
. Then there exist
$\widetilde {\gamma }_2$
. Then there exist
![]() $x_i$
in D and
$x_i$
in D and
![]() $\alpha _i\in \Gamma , i=1,2,\ldots, $
such that
$\alpha _i\in \Gamma , i=1,2,\ldots, $
such that
![]() $\alpha _ix_i$
are all in one connected component of
$\alpha _ix_i$
are all in one connected component of
![]() $\{p\in \widetilde {M}: K(p)<0\}$
and
$\{p\in \widetilde {M}: K(p)<0\}$
and
![]() $\alpha _ix_i\to w$
in T as
$\alpha _ix_i\to w$
in T as
![]() $i\to \infty $
. For i large enough, consider
$i\to \infty $
. For i large enough, consider
![]() $\alpha _i\widetilde {\gamma }_1$
and
$\alpha _i\widetilde {\gamma }_1$
and
![]() $\alpha _i\widetilde {\gamma }_2$
, which are two asymptotic non-closed flat geodesics. If
$\alpha _i\widetilde {\gamma }_2$
, which are two asymptotic non-closed flat geodesics. If
![]() $\alpha _i\widetilde {\gamma }_1$
and
$\alpha _i\widetilde {\gamma }_1$
and
![]() $\alpha _i\widetilde {\gamma }_2$
approach w, then w is a fixed point for
$\alpha _i\widetilde {\gamma }_2$
approach w, then w is a fixed point for
![]() $\alpha _i\in \Gamma $
. Then
$\alpha _i\in \Gamma $
. Then
![]() $\widetilde {\gamma }_1$
is asymptotic to an axis of
$\widetilde {\gamma }_1$
is asymptotic to an axis of
![]() $\alpha _i$
, and hence itself is closed by Lemma 4.10. This contradicts the assumption. So
$\alpha _i$
, and hence itself is closed by Lemma 4.10. This contradicts the assumption. So
![]() $\alpha _i\widetilde {\gamma }_1$
and
$\alpha _i\widetilde {\gamma }_1$
and
![]() $\alpha _i\widetilde {\gamma }_2$
approach some
$\alpha _i\widetilde {\gamma }_2$
approach some
![]() $w_i\neq w\in \widetilde {M}(\infty )$
and
$w_i\neq w\in \widetilde {M}(\infty )$
and
![]() $w_i\to w$
as
$w_i\to w$
as
![]() $i\to \infty $
. Since
$i\to \infty $
. Since
![]() $\alpha _iT$
contains
$\alpha _iT$
contains
![]() $\alpha _ix_i\in T$
, at least one of
$\alpha _ix_i\in T$
, at least one of
![]() $\alpha _i\widetilde {\gamma }_1$
and
$\alpha _i\widetilde {\gamma }_1$
and
![]() $\alpha _i\widetilde {\gamma }_2$
must intersect T. Since the considered connected component cannot intersect flat geodesics, it must be bounded. This proves the claim.
$\alpha _i\widetilde {\gamma }_2$
must intersect T. Since the considered connected component cannot intersect flat geodesics, it must be bounded. This proves the claim.
Since the radii of the inscribed disks are bounded away from zero, there exists a
![]() $t_0>0$
such that the infinite triangle
$t_0>0$
such that the infinite triangle
![]() $\widetilde {\gamma }_1(t_0)\widetilde {\gamma }_2(t_0)w$
does not contain any such inscribed disk, see Figure 4. Note that if two connected components project to the same connected component on M, they must be isometric. Thus, by the second claim above, we can find
$\widetilde {\gamma }_1(t_0)\widetilde {\gamma }_2(t_0)w$
does not contain any such inscribed disk, see Figure 4. Note that if two connected components project to the same connected component on M, they must be isometric. Thus, by the second claim above, we can find
![]() $t_1>t_0$
such that the infinite triangle
$t_1>t_0$
such that the infinite triangle
![]() $\widetilde {\gamma }_1(t_1)\widetilde {\gamma }_2(t_1)w$
is a flat region. Then
$\widetilde {\gamma }_1(t_1)\widetilde {\gamma }_2(t_1)w$
is a flat region. Then
![]() $d(\widetilde {\gamma }_1(t), \widetilde {\gamma }_2(t))\equiv d(\widetilde {\gamma }_1(t_1), \widetilde {\gamma }_2(t_1))$
for all
$d(\widetilde {\gamma }_1(t), \widetilde {\gamma }_2(t))\equiv d(\widetilde {\gamma }_1(t_1), \widetilde {\gamma }_2(t_1))$
for all
![]() $t \geq t_1$
. Indeed, if we construct a geodesic variation between
$t \geq t_1$
. Indeed, if we construct a geodesic variation between
![]() $\widetilde {\gamma }_1$
and
$\widetilde {\gamma }_1$
and
![]() $\widetilde {\gamma }_2$
, then the Jacobi fields are constant for
$\widetilde {\gamma }_2$
, then the Jacobi fields are constant for
![]() $t\geq t_1$
since
$t\geq t_1$
since
![]() $K\equiv 0$
. Thus,
$K\equiv 0$
. Thus,
![]() $d(\widetilde {\gamma }_1(t), \widetilde {\gamma }_2(t))$
is constant when
$d(\widetilde {\gamma }_1(t), \widetilde {\gamma }_2(t))$
is constant when
![]() $t \geq t_1$
. We get a contradiction since
$t \geq t_1$
. We get a contradiction since
![]() $d(\widetilde {\gamma }_1(t), \widetilde {\gamma }_2(t))\to 0$
as
$d(\widetilde {\gamma }_1(t), \widetilde {\gamma }_2(t))\to 0$
as
![]() $t \to +\infty $
by Theorem 1.8.
$t \to +\infty $
by Theorem 1.8.
Finally we can conclude that
![]() $\Lambda \subset \text {Per }(g^t)$
. In particular, the geodesic flow is ergodic by Theorem 1.7 and Pesin’s theorem (Theorem 1.3).
$\Lambda \subset \text {Per }(g^t)$
. In particular, the geodesic flow is ergodic by Theorem 1.7 and Pesin’s theorem (Theorem 1.3).
Acknowledgements
We would like to thank Keith Burns for his valuable suggestions. Some part of this paper greatly benefited from a fruitful discussion with him. The first author would also like to thank Federico Rodriguez Hertz for his help and valuable comments. The first author is supported by NSFC (Nos. 12071474, 11701559) and Fundamental Research Funds for the Central Universities (No. 20720210038). The second author is partially supported by Natural Science Foundation of Shandong Province (No. ZR2020MA017). The third author is partially supported by the State Scholarship Fund from China Scholarship Council (CSC).