Article contents
Commuting rational functions revisited
Published online by Cambridge University Press: 15 August 2019
Abstract
Let 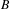 $B$ be a rational function of degree at least two that is neither a Lattès map nor conjugate to
$B$ be a rational function of degree at least two that is neither a Lattès map nor conjugate to 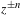 $z^{\pm n}$ or
$z^{\pm n}$ or 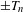 $\pm T_{n}$. We provide a method for describing the set
$\pm T_{n}$. We provide a method for describing the set 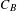 $C_{B}$ consisting of all rational functions commuting with
$C_{B}$ consisting of all rational functions commuting with 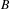 $B$. Specifically, we define an equivalence relation
$B$. Specifically, we define an equivalence relation 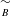 $\underset{B}{{\sim}}$ on
$\underset{B}{{\sim}}$ on 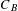 $C_{B}$ such that the quotient
$C_{B}$ such that the quotient 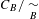 $C_{B}/\underset{B}{{\sim}}$ possesses the structure of a finite group
$C_{B}/\underset{B}{{\sim}}$ possesses the structure of a finite group 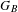 $G_{B}$, and describe generators of
$G_{B}$, and describe generators of 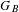 $G_{B}$ in terms of the fundamental group of a special graph associated with
$G_{B}$ in terms of the fundamental group of a special graph associated with 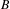 $B$.
$B$.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019
References
- 4
- Cited by



