Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-26T04:02:42.840Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBGEOMETRICALLY ERGODIC AUTOREGRESSIONS

Published online by Cambridge University Press:  09 November 2020

Mika Meitz  and
Pentti Saikkonen
Mika Meitz
Affiliation:
University of Helsinki
Pentti Saikkonen*
Affiliation:
University of Helsinki
*
Address correspondence to Pentti Saikkonen, Department of Mathematics and Statistics, University of Helsinki, P. O. Box 68, FI-00014 Helsinki, Finland; e-mail: pentti.saikkonen@helsinki.fi.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we discuss how the notion of subgeometric ergodicity in Markov chain theory can be exploited to study stationarity and ergodicity of nonlinear time series models. Subgeometric ergodicity means that the transition probability measures converge to the stationary measure at a rate slower than geometric. Specifically, we consider suitably defined higher-order nonlinear autoregressions that behave similarly to a unit root process for large values of the observed series but we place almost no restrictions on their dynamics for moderate values of the observed series. Results on the subgeometric ergodicity of nonlinear autoregressions have previously appeared only in the first-order case. We provide an extension to the higher-order case and show that the autoregressions we consider are, under appropriate conditions, subgeometrically ergodic. As useful implications, we also obtain stationarity and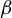 $\beta $ -mixing with subgeometrically decaying mixing coefficients.

Type
ARTICLES
Information
Econometric Theory , Volume 38 , Issue 5: YALE 2018 CONFERENCE IN HONOR OF PETER C. B. PHILLIPS: PART I , October 2022 , pp. 959 - 985
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors thank the Academy of Finland for financial support, and Peter Phillips, Donald Andrews, and two anonymous referees for useful comments and suggestions.

References

REFERENCES

Bec, F., Rahbek, A., & Shephard, N. (2008) The ACR model: A multivariate dynamic mixture autoregression. Oxford Bulletin of Economics & Statistics 70(5), 583–618.CrossRefGoogle Scholar
Bradley, R. C. (2007) Introduction to Strong Mixing Conditions, vol. 1–3. Kendrick Press.Google Scholar
Douc, R., Fort, G., Moulines, E., & Soulier, P. (2004) Practical drift conditions for subgeometric rates of convergence. Annals of Applied Probability 14(3), 1353–1377.CrossRefGoogle Scholar
Douc, R., Moulines, E., Priouret, P., & Soulier, P. (2018) Markov Chains. Springer.CrossRefGoogle Scholar
Doukhan, P. (1994) Mixing: Properties and Examples. Springer.CrossRefGoogle Scholar
Fokianos, K., Rahbek, A., & Tjøstheim, D. (2009) Poisson autoregression. Journal of the American Statistical Association 104, 1430–1439.CrossRefGoogle Scholar
Fort, G. & Moulines, E. (2003) Polynomial ergodicity of Markov transition kernels. Stochastic Processes and Their Applications 103(1), 57–99.CrossRefGoogle Scholar
Francq, C. & Zakoïan, J.-M. (2006) Mixing properties of a general class of GARCH(1,1) models without moment assumptions on the observed process. Econometric Theory 22(5), 815–834.CrossRefGoogle Scholar
Gouriéroux, C. & Robert, C. Y. (2006) Stochastic unit root models. Econometric Theory 22(6), 1052–1090.CrossRefGoogle Scholar
Horn, R. A. & Johnson, C. R. (2013) Matrix Analysis, 2nd Edition. Cambridge University Press.Google Scholar
Jarner, S. F. & Tweedie, R. L. (2003) Necessary conditions for geometric and polynomial ergodicity of random-walk-type Markov chains. Bernoulli 9(4), 559–578.CrossRefGoogle Scholar
Klokov, S. A. (2007) Lower bounds of mixing rate for a class of Markov processes. Theory of Probability and Its Applications 51(3), 528–535.CrossRefGoogle Scholar
Klokov, S. A. & Veretennikov, A. Yu. (2004) Sub-exponential mixing rate for a class of Markov chains. Mathematical Communications 9, 9–26.Google Scholar
Klokov, S. A. & Veretennikov, A. Yu. (2005) On subexponential mixing rate for Markov processes. Theory of Probability and Its Applications 49(1), 110–122.CrossRefGoogle Scholar
Lieberman, O. & Phillips, P. C. B. (2020) Hybrid stochastic local unit roots. Journal of Econometrics 215(1), 257–285.CrossRefGoogle Scholar
Ling, S. (2007) A double AR( $p$ ) model: Structure and estimation. Statistica Sinica 17(1), 161–175.Google Scholar
Lu, Z. (1998) On the geometric ergodicity of a non-linear autoregressive model with an autoregressive conditional heteroscedastic term. Statistica Sinica 8, 1205–1217.Google Scholar
Meitz, M. & Saikkonen, P. (2008) Ergodicity, mixing, and existence of moments of a class of Markov models with applications to GARCH and ACD models. Econometric Theory 24(5), 1291–1320.CrossRefGoogle Scholar
Meitz, M. & Saikkonen, P. (2019) Subgeometric ergodicity and $\beta$ -mixing, arXiv:1904.07103.Google Scholar
Meyn, S. P. & Tweedie, R. L. (1993) Markov Chains and Stochastic Stability. Springer.CrossRefGoogle Scholar
Meyn, S. P. & Tweedie, R. L. (2009) Markov Chains and Stochastic Stability, 2nd Edition. Cambridge University Press.CrossRefGoogle Scholar
Nummelin, E. & Tuominen, P. (1983) The rate of convergence in Orey’s theorem for Harris recurrent Markov chains with applications to renewal theory. Stochastic Processes and Their Applications 15(3), 295–311.CrossRefGoogle Scholar
Tanikawa, A. (2001) Markov chains satisfying simple drift conditions for subgeometric ergodicity. Stochastic Models 17(2), 109–120.CrossRefGoogle Scholar
Tuominen, P. & Tweedie, R. L. (1994) Subgeometric rates of convergence of $f$ -ergodic Markov chains. Advances in Applied Probability 26(3), 775–798.CrossRefGoogle Scholar
van Dijk, D., Teräsvirta, T., & Franses, P. H. (2002) Smooth transition autoregressive models—A survey of recent developments. Econometric Reviews 21(1), 1–47.CrossRefGoogle Scholar
Veretennikov, A. Yu. (2000) On polynomial mixing and convergence rate for stochastic difference and differential equations. Theory of Probability and Its Applications 44(2), 361–374.CrossRefGoogle Scholar
Supplementary material: PDF

Meitz and Saikkonen supplementary material

Appendix

Download Meitz and Saikkonen supplementary material(PDF)
PDF 702.2 KB