Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T21:39:43.907Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBGEOMETRICALLY ERGODIC AUTOREGRESSIONS WITH AUTOREGRESSIVE CONDITIONAL HETEROSKEDASTICITY

Published online by Cambridge University Press:  17 November 2023

Mika Meitz Open the ORCID record for Mika Meitz [Opens in a new window]  and
Pentti Saikkonen
Mika Meitz*
Affiliation:
University of Helsinki
Pentti Saikkonen
Affiliation:
University of Helsinki
*
Address correspondence to Mika Meitz, Department of Economics, University of Helsinki, P. O. Box 17, FI-00014 University of Helsinki, Finland; e-mail: mika.meitz@helsinki.fi.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider subgeometric (specifically, polynomial) ergodicity of univariate nonlinear autoregressions with autoregressive conditional heteroskedasticity (ARCH). The notion of subgeometric ergodicity was introduced in the Markov chain literature in the 1980s, and it means that the transition probability measures converge to the stationary measure at a rate slower than geometric; this rate is also closely related to the convergence rate of 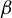$\beta $-mixing coefficients. While the existing literature on subgeometrically ergodic autoregressions assumes a homoskedastic error term, this paper provides an extension to the case of conditionally heteroskedastic ARCH-type errors, considerably widening the scope of potential applications. Specifically, we consider suitably defined higher-order nonlinear autoregressions with possibly nonlinear ARCH errors and show that they are, under appropriate conditions, subgeometrically ergodic at a polynomial rate. An empirical example using energy sector volatility index data illustrates the use of subgeometrically ergodic AR–ARCH models.

Type
ARTICLES
Information
Econometric Theory , First View , pp. 1 - 31
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Footnotes

The authors thank the Academy of Finland (M.M. and P.S.), Foundation for the Advancement of Finnish Securities Markets (M.M.), and OP Group Research Foundation (M.M.) for financial support, and the Co-Editor (Robert Taylor) and three anonymous referees for useful comments and suggestions.

References

REFERENCES

Atchadé, Y., & Fort, G. (2010) Limit theorems for some adaptive MCMC algorithms with subgeometric kernels. Bernoulli 16, 116–154.CrossRefGoogle Scholar
Cline, D. B. H. (2007) Stability of nonlinear stochastic recursions with application to nonlinear AR–GARCH models. Advances in Applied Probability 39, 462–491.CrossRefGoogle Scholar
Cline, D. B. H., & Pu, H. H. (1998) Verifying irreducibility and continuity of a nonlinear time series. Statistics & Probability Letters 40, 139–148.CrossRefGoogle Scholar
Cline, D. B. H., & Pu, H. H. (2004) Stability and the Lyapounov exponent of threshold AR–ARCH models. Annals of Applied Probability 14, 1920–1949.CrossRefGoogle Scholar
Davidson, J. (1994) Stochastic Limit Theory . Oxford University Press.CrossRefGoogle Scholar
Douc, R., Fort, G., Moulines, E., & Soulier, P. (2004) Practical drift conditions for subgeometric rates of convergence. Annals of Applied Probability 14, 1353–1377.CrossRefGoogle Scholar
Douc, R., Guillin, A., & Moulines, E. (2008) Bounds on regeneration times and limit theorems for subgeometric Markov chains. Annales de l’Institute Henri Poincare, Probabilites et Statistiques 44, 239–257.Google Scholar
Douc, R., Moulines, E., Priouret, P., & Soulier, P. (2018) Markov Chains . Springer.CrossRefGoogle Scholar
Dudley, R. M. (2004) Real Analysis and Probability . Cambridge University Press.Google Scholar
Engle, R. F. (1982) Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50, 987–1007.CrossRefGoogle Scholar
Fefferman, C., & Shapiro, H. S. (1972) A planar face on the unit sphere of the multiplier space ${M}_p$ , $1<p<\infty$ . Proceedings of the American Mathematical Society 36, 435–439.Google Scholar
Fort, G., & Moulines, E. (2000) V-subgeometric ergodicity for a Hastings–Metropolis algorithm. Statistics & Probability Letters 49, 401–410.CrossRefGoogle Scholar
Fort, G., & Moulines, E. (2003) Polynomial ergodicity of Markov transition kernels. Stochastic Processes and Their Applications 103, 57–99.CrossRefGoogle Scholar
Horn, R. A., & Johnson, C. R. (2013) Matrix Analysis . (2nd ed.) Cambridge University Press.Google Scholar
Jarner, S. F., & Roberts, G. O. (2002) Polynomial convergence rates of Markov chains. Annals of Applied Probability 12, 224–247.CrossRefGoogle Scholar
Jones, M. C., & Faddy, M. J. (2003) A skew extension of the $t$ -distribution, with applications. Journal of the Royal Statistical Society: Series B 65, 159–174.CrossRefGoogle Scholar
Klokov, S. A. (2007) Lower bounds of mixing rate for a class of Markov processes. Theory of Probability and Its Applications 51, 528–535.CrossRefGoogle Scholar
Klokov, S. A., & Veretennikov, A. Y. (2004) Sub-exponential mixing rate for a class of Markov chains. Mathematical Communications 9, 9–26.Google Scholar
Klokov, S. A., & Veretennikov, A. Y. (2005) On subexponential mixing rate for Markov processes. Theory of Probability and Its Applications 49, 110–122.CrossRefGoogle Scholar
Lieberman, O., & Phillips, P. C. B. (2020) Hybrid stochastic local unit roots. Journal of Econometrics 215, 257–285.CrossRefGoogle Scholar
Ling, S. (1999) On the probabilistic properties of a double threshold ARMA conditional heteroskedastic model. Journal of Applied Probability 36, 688–705.CrossRefGoogle Scholar
Ling, S., & McAleer, M. (2002) Necessary and sufficient moment conditions for the GARCH( $r$ , $s$ ) and asymmetric power GARCH( $r$ , $s$ ) models. Econometric Theory 18, 722–729.CrossRefGoogle Scholar
Liu, J., Li, W. K., & Li, C. W. (1997) On a threshold autoregression with conditional heteroscedastic variances. Journal of Statistical Planning and Inference 62, 279–300.CrossRefGoogle Scholar
Meitz, M., & Saikkonen, P. (2008a) Ergodicity, mixing, and existence of moments of a class of Markov models with applications to GARCH and ACD models. Econometric Theory 24, 1291–1320.CrossRefGoogle Scholar
Meitz, M., & Saikkonen, P. (2008b) Stability of nonlinear AR–GARCH models. Journal of Time Series Analysis 29, 453–475.CrossRefGoogle Scholar
Meitz, M., & Saikkonen, P. (2010) A note on the geometric ergodicity of a nonlinear AR–ARCH model. Statistics & Probability Letters 80, 631–638.CrossRefGoogle Scholar
Meitz, M., & Saikkonen, P. (2021) Subgeometric ergodicity and $\beta$ -mixing. Journal of Applied Probability 58, 594–608.CrossRefGoogle Scholar
Meitz, M., & Saikkonen, P. (2022) Subgeometrically ergodic autoregressions. Econometric Theory 38, 959–985.CrossRefGoogle Scholar
Merlevède, F., Peligrad, M., & Rio, E. (2011) A Bernstein type inequality and moderate deviations for weakly dependent sequences. Probability Theory and Related Fields 151, 435–474.CrossRefGoogle Scholar
Meyn, S. P., & Tweedie, R. L. (2009) Markov Chains and Stochastic Stability . (2nd ed.) Cambridge University Press.CrossRefGoogle Scholar
Nummelin, E., & Tuominen, P. (1983) The rate of convergence in Orey’s theorem for Harris recurrent Markov chains with applications to renewal theory. Stochastic Processes and Their Applications 15, 295–311.CrossRefGoogle Scholar
Phillips, P. C. B. (2023) Estimation and inference with near unit roots. Econometric Theory 39, 221–263.CrossRefGoogle Scholar
Tuominen, P., & Tweedie, R. L. (1994) Subgeometric rates of convergence of $f$ -ergodic Markov chains. Advances in Applied Probability 26, 775–798.CrossRefGoogle Scholar
Tweedie, R. L. (1983) Criteria for rates of convergence of Markov chains, with application to queueing and storage theory. In Kingman, J. F. C., & Reuter, G. E. H. (Eds.), Probability, Statistics and Analysis , pp. 260–276. Cambridge University Press.CrossRefGoogle Scholar
Veretennikov, A. Y. (2000) On polynomial mixing and convergence rate for stochastic difference and differential equations. Theory of Probability and Its Applications 44, 361–374.CrossRefGoogle Scholar
Vladimirova, M., Girard, S., Nguyen, H., & Arbel, J. (2020) Sub-Weibull distributions: Generalizing sub-Gaussian and sub-exponential properties to heavier tailed distributions. Stat 9, e318.CrossRefGoogle Scholar
Wong, K. C., Li, Z., & Tewari, A. (2020) Lasso guarantees for $\beta$ -mixing heavy-tailed time series. Annals of Statistics 48, 1124–1142.CrossRefGoogle Scholar