1 Introduction
Thermoelectric effect has the potential to recover waste heat, which amounts to 50% of the global energy usage. Currently, the usage of technology is limited to niche applications (e.g., spacecraft) due to the low efficiency, rare elements, and toxic constituents (e.g., Bi, Te etc.) of thermoelectric (TE) materials. Oxide ceramics (e.g., ZnO, CaMnO3, and SrTiO3) have attracted a lot of attention for high-temperature applications, such as waste heat recovery in industrial power plants, automobiles, and so forth, due to their excellent high temperature stability, environment friendly constituents and cheaper mass production methods (Ovik et al., Reference Ovik, Long, Barma, Riaz, Sabri, Said and Saidur2016; He et al., Reference He, Liu and Funahashi2011; Koumoto et al., Reference Koumoto, Terasaki and Funahashi2006). High electrical conductivity and Seebeck coefficient can be achieved in suitable oxide TE materials by transient element doping and band gap engineering (Ohta et al., Reference Ohta, Sugiura and Koumoto2008; Fergus, Reference Fergus2012). However, their inherent high thermal conductivity results into low thermoelectric efficiency (ZT < 0.5), which is defined as ZT =
$ {\alpha}^2\sigma T/k $
, where
$ \alpha $
,
$ \sigma $
, k, and T are Seebeck coefficient, electrical conductivity, thermal conductivity, and temperature, respectively. For any practical applications, TE materials with ZT > 1 are required to make TE energy a commercially viable alternative for waste heat recovery.
On the experimental side, study of oxide TE materials has mostly focused on developing phonon glass–electron crystal structures (He et al., Reference He, Liu and Funahashi2011), which allows decoupling of the electron and phonon transport properties. Enhancing the hierarchical scattering of phonons through nanostructuring mechanisms have been major focus in developing thermoelectric oxides. Incorporation of sintering additives has been commonly used strategy to introduce hierarchical phonon scattering (Wang et al., Reference Wang, He, Ba, Wan and Koumoto2010; Buscaglia et al., Reference Buscaglia, Maglia, Anselmi-Tamburini, Marré, Pallecchi, Ianculescu, Canu, Viviani, Fabrizio and Buscaglia2014; Lan et al., Reference Lan, Lin, Liu, Xu and Nan2012). Jood et al. (Reference Jood, Mehta, Zhang, Peleckis, Wang, Siegel, Borca-Tasciuc, Dou and Ramanath2011) reported a reduction upto 2 W/mK in the thermal conductivity of the Al-doped nanostructured ZnO. Azough et al. (Reference Azough, Gholinia, Alvarez-Ruiz, Duran, Kepaptsoglou, Eggeman, Ramasse and Freer2019) reported core-shell type of nanostructure formation within the grains in B doped SrTiO3 ceramics leading to a low
$ {k}_L $
value of 2.75 W/mK. Microstructural anisotropy introduced through Al-induced variations in oxygen stoichiometry can also enhance phonon scattering in preferential directions (Abutaha et al., Reference Abutaha, Sarath Kumar and Alshareef2013; Han et al., Reference Han, Van Nong, Zhang, Holgate, Tashiro, Ohtaki, Pryds and Linderoth2014). Hybrid superlattice type of structures have also been experimented for enhanced scattering of phonons at the interfaces in ZnO (Giri et al., Reference Giri, Niemelä, Tynell, Gaskins, Donovan, Karppinen and Hopkins2016) and SrTiO3 (Abutaha et al., Reference Abutaha, Kumar, Li, Dehkordi, Tritt and Alshareef2015). Alvarez-Ruiz et al. (Reference Alvarez-Ruiz, Azough, Hernandez-Maldonado, Kepaptsoglou, Ramasse, Day, Svec, Svec and Freer2018) reported unit cell twinning in Ga-doped ZnO, which start acting as phonon scattering centers. Introduction of structural defects using controlled synthesis methods can also help reduce
$ {k}_L $
. Magnéli phases of TiO2 have intrinsic, layered nanostructures defined by crystallographic shear planes, which act as scattering centers (Kieslich et al., Reference Kieslich, Cerretti, Veremchuk, Hermann, Panthöfer, Grin and Tremel2016). Takemoto et al. (Reference Takemoto, Fugane, Yan, Drennan, Saito, Mori and Yamamura2014) reported the formation of a dense structure of three-dimensional (3D) stacking faults along the basal and pyramidal planes lowering
$ {k}_L $
values upto 1.7 Wm/K in ZnO codoped with In and Ga. Zihua et al. (Reference Zihua, Huaqing, Yuanyuan, Jiaojiao and Jianhui2018) introduced another level of nanostructuring by incorporating organic nanoparticles in the Co-doped ZnO.
In addition to experimental research, there are continuing efforts to bridge the gaps in our understanding of phonon scattering mechanisms using multiscale simulations to bring in the next generation of advances. Wu et al. (Reference Wu, Lee, Varshney, Wohlwend, Roy and Luo2016) applied first principle lattice dynamics to understand heat conduction mechanism in pure w-ZnO. Lower thermal conductivity of ZnO was attributed to smaller phonon group velocities, larger three-phonon scattering phase space, and larger anharmonicity in ZnO. It was also shown that ZnO possesses anisotropic thermal conductivity along the [1000] and [0001] directions, which has also been observed experimentally (Liang and Wang, Reference Liang and Wang2020). Duda et al. (Reference Duda, English, Jordan, Norris and Soffa2012) conducted nonequilibrium molecular dynamics simulations to understand the effect of ordering of solid solutions. The results showed that ordering of solid solutions leads to change in the dominant scattering mechanism from impurity scattering to Umklapp three-phonon scattering. Wu et al. (Reference Wu, Su, Pao and Shih2019) calculated the thermal conductivity of Silicon rich oxide layers inserted ZnO superlattice using the reverse nonequilibrium molecular dynamics method. Reduction in
$ {k}_L $
was attributed to the phonon scattering at the ZnO/Si interface as well as the grain boundaries. Wang et al. (Reference Wang, Qin, Li, Wang and Hu2017) studied the thermal conductivity of 2D ZnO monolayer and its anomalous temperature dependence using first principle density functional theory (DFT) simulations. Abnormally, slower fall in
$ {k}_L $
with increasing T was found due to the significant contribution of optical phonon modes in overall thermal transport. Zhang and Koumoto (Reference Zhang and Koumoto2013) showed that the thermal conductivity of SrTiO3 superlattice decreases with decreasing grain size due to enhanced interface scattering.
High dimensionality of design space of thermoelectric materials makes the optimization of design parameters a nontrivial task. It is evident from the literature analysis that the class of materials explored for TE applications has been rather limited so far and our understanding of electronic and phonon transport of crystalline alloys is fairly limited (Minnich et al., Reference Minnich, Dresselhaus, Ren and Chen2009). On the other hand, rapid developments in the field of materials informatics has helped researchers explore new class of promising materials and establish correlations between design parameters and the thermoelectric properties (Wang et al., Reference Wang, Zhang, Snoussi and Zhang2019). Wang et al. (Reference Wang, Wang, Setyawan, Mingo and Curtarolo2011) used high-throughput ab-initio calculations combined with regression analysis to show a positive correlation between power factor and the band gap and the charge carrier effective mass. Materials with large number of atoms per unit cell tend to have high power factor. Gaultois et al. (Reference Gaultois, Sparks, Borg, Seshadri, Bonificio and Clarke2013) conducted a data centric review of TE research literature creating a database of over 18,000 data points from over 100 publications. They used elaborate visualization techniques to extract the information of materials with promising thermoelectric properties along with their nature resource availability. They also designed a web-based recommendation engine based on random forest algorithm, which takes Seebeck coefficient, electrical conductivity, thermal conductivity, and band gap to evaluate the TE potential of a material (Oliynyk et al., Reference Oliynyk, Antono, Sparks, Ghadbeigi, Gaultois, Meredig and Mar2016). High-throughput materials modeling combined with machine learning (ML) methods showed that large lattice parameter, band gap, and effective mass of holes are the key properties for high TE efficiency of nanograined half-heusler compounds (Carrete et al., Reference Carrete, Li, Mingo, Wang and Curtarolo2014). Novel semiconductors with ultralow
$ {k}_L $
values were proposed for further experimental studies (Carrete et al., Reference Carrete, Li, Mingo, Wang and Curtarolo2014). McKinney et al. (Reference McKinney, Gorai, Stevanović and Toberer2017) conducted high-throughput computational search for low Lorentz number materials for TE application. In addition to confirming existing TE materials, several new classes of materials were found, such as Zintl compounds and n-type ternary diamond-like semiconductors. Iwasaki et al. (Reference Iwasaki, Takeuchi, Stanev, Kusne, Ishida, Kirihara, Ihara, Sawada, Terashima, Someya, Uchida, Saitoh and Yorozu2019) used supervised ML models to establish the key physical parameters controlling spin driven thermoelectric effect and proposed a novel material showing promising results. Oliynyk et al. (Reference Oliynyk, Antono, Sparks, Ghadbeigi, Gaultois, Meredig and Mar2016) found that electron count of B and difference in the atomic sizes of A and B are the most influential parameters in AB2C type of compounds using random forest ML algorithm. Hou et al. (Reference Hou, Takagiwa, Shinohara, Xu and Tsuda2019) used ML-based methods to optimize the Al/Si ratio in off-stochiometric Al23.5+x
Fe36.5Si40−x
compounds for achieving highest power factor. Miller et al. (Reference Miller, Gorai, Aydemir, Mason, Stevanović, Toberer and Snyder2017) used high-throughput computations to screen 735 oxide materials for their thermoelectric properties and identified SnO as a potential n-type TE material. Measurements showed an extremely low k of 0.75 W/mK at moderate temperatures and ZT values of 0.22 in synthesized samples.
Application of ML algorithms on small datasets frequently encountered in materials science has been a key issue in materials informatics. Zhang and Ling (Reference Zhang and Ling2018) proposed to include a crude estimate of the target property using low fidelity models as a way to improve the accuracy of ML models applied on small datasets. They achieved a high accuracy in predicting
$ {k}_L $
by including empirical slack model values of
$ {k}_L $
as a descriptor in the ML model. Singh and coworkers (Juneja et al., Reference Juneja, Yumnam, Satsangi and Singh2019; Juneja et al., Reference Juneja and Singh2020a; Juneja et al., Reference Juneja and Singh2020b) combined ML with high-throughput computing to build regression models for predicting the
$ {k}_L $
of inorganic compounds. They also used maximum phonon frequency and integrated Gruneisen parameter as descriptors to build ML models for predicting
$ {k}_L $
. Both the ML models to predict the
$ {k}_L $
used complex derived properties as descriptors in their ML models, which restricts their utility in the initial phases of material selection and design. ML models based on characteristic materials properties are required to be used effectively in the discovery of new materials and reduce the time of design cycle.
In this work, we have applied a two-step ML-based process to first classify low
$ {k}_L $
transition metal oxides and then predict their
$ {k}_L $
values using regression methods. The proposed two-step process has been showed to be able to accurately predict the
$ {k}_L $
values using a small dataset of transition metal oxides comprising 315 compounds. In this process, we were also able to define key fundamental material properties, which can be used for the screening of low
$ {k}_L $
compounds in the initial stages of material design. The ML process has been described in detail in Section 2 and results are discussed in Section 3.
2 Computational Methods
In this paper, the statistical methods employed are propelled mainly by the data gathered from Automatic-FLOW (AFLOW) for Materials Discovery database. The details of the database can be found elsewhere (Curtarolo et al., Reference Curtarolo, Setyawan, Hart, Jahnatek, Chepulskii, Taylor, Wang, Xue, Yang, Levy, Mehl, Stokes, Demchenko and Morgan2012). AFLOW uses the Gibbs implementation of quasiharmonic Debye–Gruneisen model to calculate the lattice thermal conductivity (
$ {k}_L $
) of the compounds (Toher et al., Reference Toher, Oses, Plata, Hicks, Rose, Levy, de Jong, Asta, Fornari, Nardelli and Curtarolo2017). First principle-based DFT calculations are performed for calculating the acoustic Debye temperature and Slater-Gamma method is used to calculate the Gruneisen parameter, which are then used in the calculation of
$ {k}_L $
. Oxides and oxide alloys of transition metals, that is elements of groups 3–11 and periods 4–6 were considered in the present study as they have shown promise for high temperature thermoelectric applications (Ovik et al., Reference Ovik, Long, Barma, Riaz, Sabri, Said and Saidur2016; Yin et al., Reference Yin, Tudu and Tiwari2017). The compounds considered in the present study had
$ {k}_L $
ranging from 0.017 to 59.63 W/mK. The aim of the current study was to identify the most influencing fundamental properties affecting
$ {k}_L $
of these compounds as well as build ML-based multifidelity surrogate models to predict the
$ {k}_L $
of the transition metal oxides.
In order to do so, we implemented a two-step process (Figure 1): classification and regression. In the first step, we built a ML classifier to screen out unknown compounds having low
$ {k}_L $
(<5). The same classifier model was also used to shortlist the most influencing fundamental material properties. The second step was to build a regression-based predictive model, which can be used to determine the numerical values of
$ {k}_L $
of a compound. In the following, we describe both of these steps in detail.
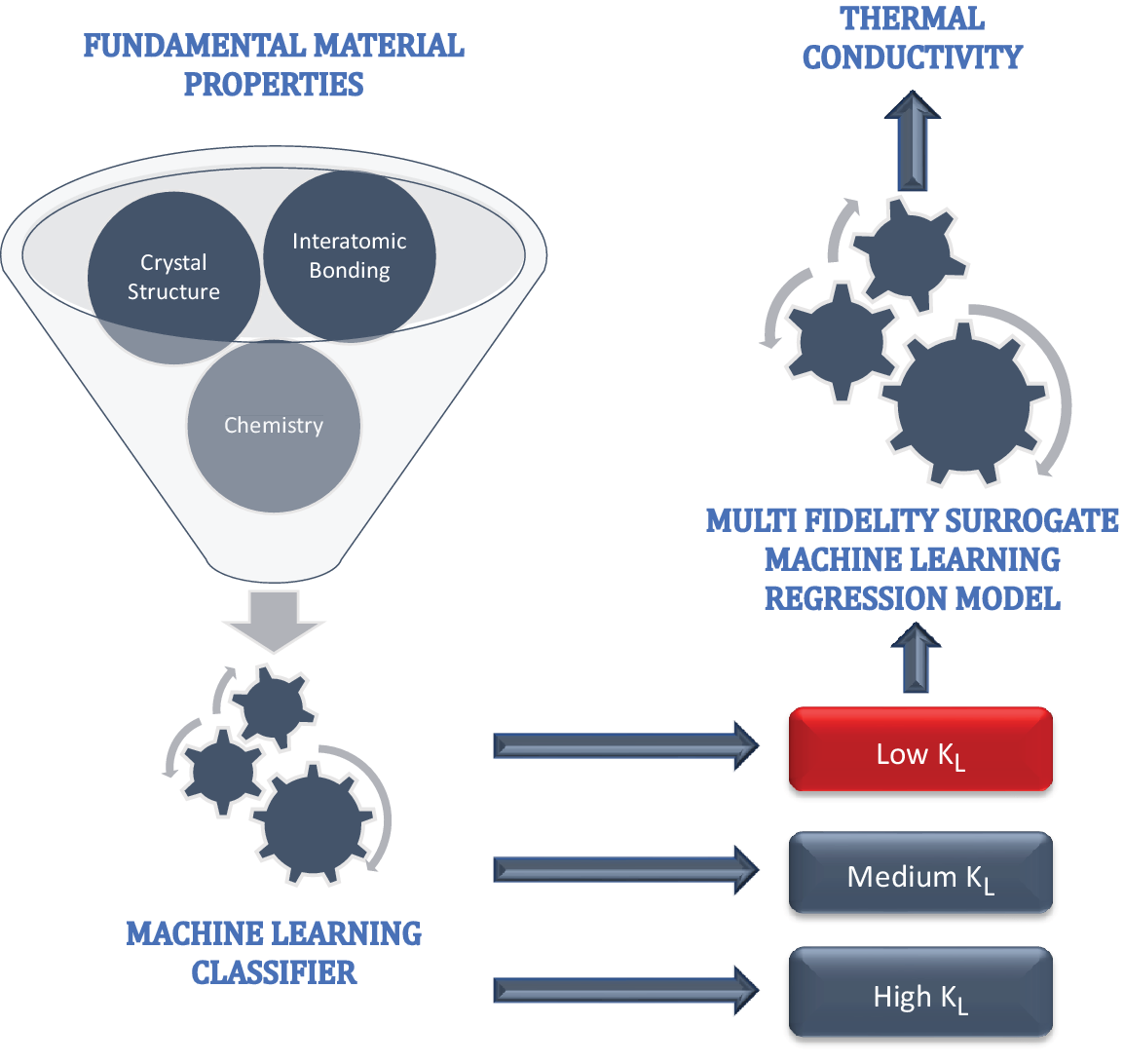
Figure 1. Two-step machine learning process, where the first step filters low
$ {k}_L $
compounds using only fundamental material properties, such as details about crystal structure, interatomic bonding, and compound chemistry. In the second step, a multifidelity machine learning surrogate regression model is built to predict numerical
$ {k}_L $
values.
2.1 Classification
The successful application of ML approaches on the modeling of material properties requires the selection of an appropriate set of modeling variables, namely the descriptors for the property of interest. In general, the descriptors are expected to be capable of both sufficiently distinguishing each of the modeled compounds/materials and determining the targeted property.
In order to select the most influential features, we used following fundamental materials properties to build a classification model: mass density (
$ {\rho}_m $
), ratio of oxygen to transition metal atom (O/M ratio), Bravias lattice type, atom density (
$ {\rho}_n $
), electronic energy band gap (
$ {E}_g $
), lattice energy per atom (
$ {e}_L $
), point group order (O), and c/a ratio. Above mentioned parameters describe the crystal structure, compound chemistry, and interatomic bonding of an alloy. The idea was to use only fundamental crystal and materials properties so that they can be used as design parameters in the early stages of selection and shortlisting. Other ML models reported in the literature use complex derived properties, such as Gruneisen parameter, maximum phonon frequency, empirically estimated thermal conductivity (Juneja et al. (Reference Juneja, Yumnam, Satsangi and Singh2019); Wang et al., Reference Wang, Zhang, Snoussi and Zhang2019), which makes the utility of ML models rather limited. Classification model was built to segregate compounds into three categories of
$ {k}_L $
viz. low (
$ {k}_L $
< 5 W/mK), medium (5 <
$ {k}_L $
< 10 W/mK), and high (
$ {k}_L $
> 10 W/mK). In this way, the resulting model could potentially capture the underlying physical mechanisms after training, and thus offer reliable predictions for the chemistries beyond the training set. Around 30 different ML and deep learning models were built using the Caret library in R to solve this ternary classification task.
Best performance was achieved with Gradient Boosting Trees (details about the model training procedure are mentioned in Supplementary Appendix: Figure S5) in which the loss function to be optimized is in terms of trees grown on subsets of the predictor space. The algorithm XGBoost (Chen and Guestrin, Reference Chen and Guestrin2016) achieves this task in a computationally efficient manner. This method has the potential to overfit data to any extent to give low prediction error rates. Xgboost algorithm has been widely used by data scientists in diverse problems involving classification and regression. Boosting is an ensemble technique where new tree-based models are added to correct the errors made by existing tree models. Tree-models are added sequentially until no further improvements can be made. Gradient boosting is an approach where new models are created that predict the residuals or errors of prior models and then added together to make the final prediction.
2.2 Regression
In this step, we used regression ML models to predict the absolute value of
$ {k}_L $
of a compound. Since our dataset contained about 315 observations and 11 features (including the target variable), the dataset is relatively small. This may lead to higher variance in the least square estimates (Zhang and Ling, Reference Zhang and Ling2018). Regularization based regression techniques such as Lasso, Kernel-Ridge, Elastic net, and their modifications help us solve this problem by reducing the variance while managing negligible increase in bias. These models have been used extensively in the past by the computational materials community (Zhang and Ling, Reference Zhang and Ling2018; Hu et al., Reference Hu, Zhao, Zhang, Bin, Del Rose, Zhao, Zu, Chen, Sun, de Jong and Qi2020) to build regression models with small sized datasets.
The Caret library in R (Kuhn et al., Reference Kuhn2008) and the AutoML (H2O.ai, 2017) library from H2O package were used to automate the process of building regression models, thus automating the end-to-end process of applying ML to real-world problems. AutoML tends to automate the maximum number of steps in an ML pipeline with a minimum amount of human effort without compromising the model’s performance.
Due to the ease provided by these libraries, we were able to test the performance of a large number of predictive ML and deep learning models through cross validation on our dataset of thermoelectric oxides. Since we are interested in low
$ {k}_L $
oxide alloys, we decided to build the regression model using the already classified data of only low
$ {k}_L $
alloys, which contained 131 data points. The first regression model was built by considering the same descriptors, which were used to build the classification models in the first step. The best performing model (Random Forest) gave an
$ {R}^2 $
value of 0.70. To improve the predictive accuracy of our model, we included two additional descriptors: Gruneisen parameter and Debye temperature, which have also been used earlier to build ML models for
$ {k}_L $
prediction (Juneja et al., Reference Juneja, Yumnam, Satsangi and Singh2019). Best performance was achieved with cubist regression (details about the model training procedure are mentioned in Supplementary Appendix: Figure S6) which largely follows the model tree approach proposed by Quinlan et al. (Reference Quinlan1992). The basic idea behind the model tree approach is to use linear models instead of mere average of responses in the terminal leaves. This makes the method fit better than a Random Forest model in case the true responses are too large or too small. Even the splitting criteria chosen is differently as the expected reduction in the error of the node. Further, model trees deal with the problem of overfitting by incorporating a smoothing strategy devoled by Hastie and Pregibon (Reference Hastie and Pregibon1990). The smoothing process adopted by Cubist is however more complex in comparison to model trees. For precise mathematical details the reader is refered to Kuhn and Johnson (Reference Kuhn and Johnson2013).
3 Results and Discussions
A dataset of 315 compounds was obtained from AFLOW materials database. For the classification model, data for compounds was labeled based on the values of
$ {k}_L $
as “low” (
$ {k}_L $
<5 W/mK), “medium” (0 <
$ {k}_L $
< 10 W/mK), and “high” (
$ {k}_L $
> 10 W/mK). Equal instances of all the three classes were used to train the classifier to avoid class imbalance. The performance of top seven algorithms after training, testing, and hyperparameter tuning using 10-fold cross-validation is plotted in Figure 2. Using 10-fold cross validation while training the models allows us to divide the data into 10 parts out of which 9 are iteratively used for training and the last one for testing. Out of 30 different ML and deep learning models, both XGBoost and Random Forest models offer superior accuracy when compared to other counterparts such as Naïve Bayes, support vector machines (SVM), k Nearest Neighbors (kNN), linear discriminant analysis (LDA), and deep learning based classifiers. Higher value of cohens kappa coefficient also verifies their superiority. XGBoost was chosen for further analysis on the basis of higher mean class probability when compared to Random Forest. We notice that boosting (combining many weak learners to form a strong learner), plays a significant role in the success of tree-based classifiers for the limited data regime in materials sciences.
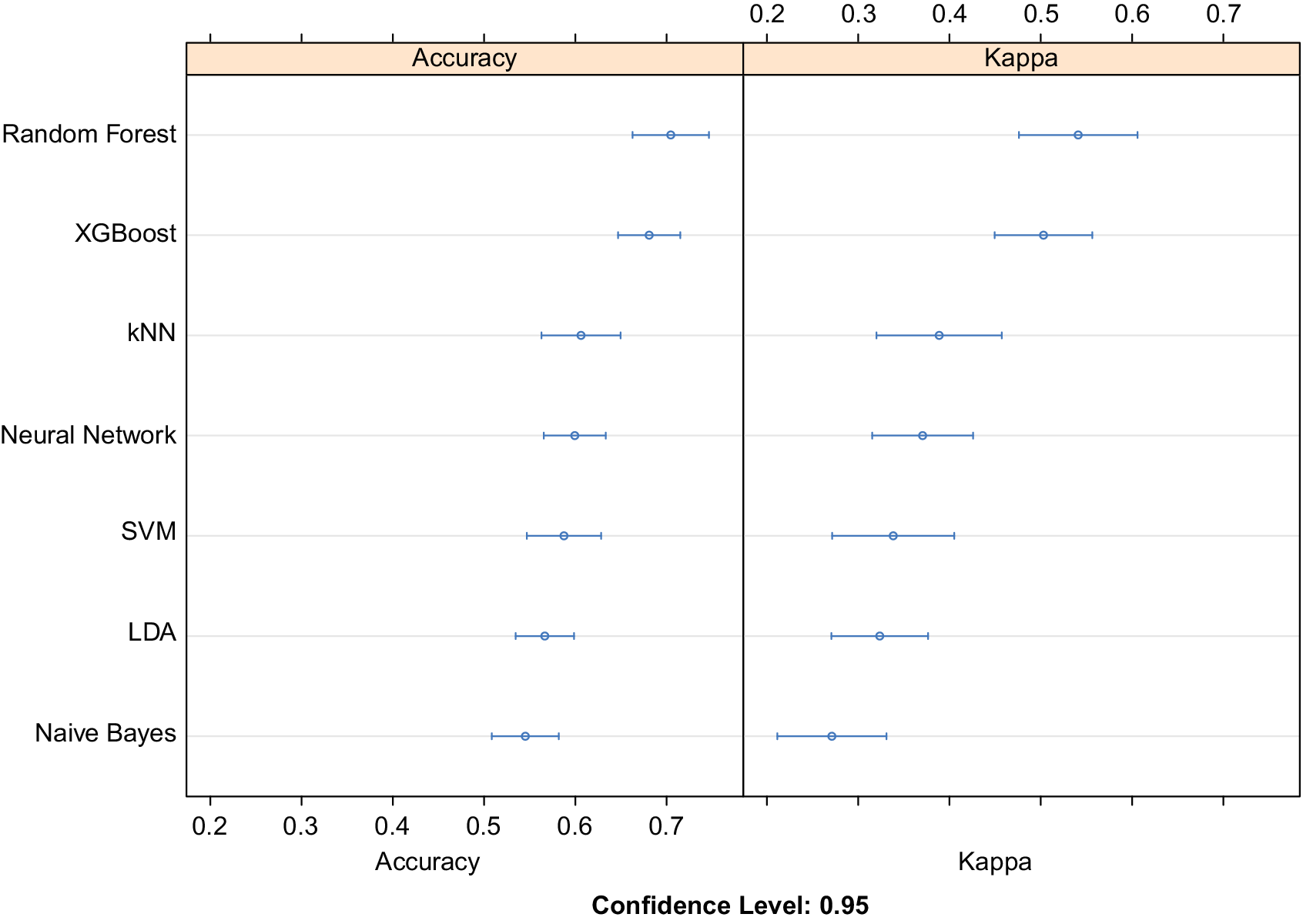
Figure 2. Relative comparison of accuracy obtained using machine learning and deep learning classifiers. Here XGBoost and Random Forest surpass deep neural networks and other machine learning approaches to obtain the best classification accuracy. Cohen’s kappa coefficient is also used to evaluate the different classification models amongst themselves. Abbreviations: kNN, k Nearest Neighbors; SVM, support vector machine with rbf kernel; LDA, linear discriminant analysis.
The XGBoost classifier correctly identified unknown compounds having Low
$ {k}_L $
(sensitivity) with an accuracy of 81% and correctly identified unknown compounds not having Low
$ {k}_L $
(specificity) with an accuracy of 82%. The balanced accuracy achieved while detecting compounds having high
$ {k}_L $
was 84%. A dip in accuracy was observed while distinguishing low from medium
$ {k}_L $
compounds and medium from high
$ {k}_L $
compounds as the accuracy in such cases was 70%. The overall accuracy obtained while categorizing new compounds into the correct category was 72.13%. Table 1 represents the confusion matrix for model predictions on the validation set.
Table 1. Confusion Matrix for predictions made on the validation set by the XGBoost classifier.
In order to assess the pros and cons of different classifiers, we went even further to calculate the probability of the class predicted by various methods for the given test observations. The average value of these probabilities are shown in Table 2. The class probabilities represent the confidence with which an unknown compound gets assigned to a particular class; therefore, higher values make the predictions trustworthy. Once again, XGBoost performs the best in this regard as well. We also computed the multi class area under the receiver operating characteristics (AUROC) values for the various methods according to the definition laid down by Hand and Till (Reference Hand and Till2001). It tells how much model is capable of distinguishing between classes. Higher the AUROC, better the model is at distinguishing between classes. These numbers are summarized in Table 2. XGBoost clearly outscores the other methods in this regard.
Table 2. A detailed comparison of different classifiers and their relative performance.
Here mean class probability represents the average confidence with which the classifier assigns a particular compound to the predicted class. The corresponding sensitivities and specificities have also been mentioned.
Abbreviation: AUROC, area under the receiver operating characteristics; kNN, k Nearest Neighbors; LDA, linear discriminant analysis; SVM, support vector machine.
The benefit of using XGBoost as the classifier is that after the boosted trees are constructed, it is relatively straightforward to retrieve importance scores for each attribute. Generally, importance provides a score that indicates how useful or valuable each feature was in the construction of the boosted decision trees within the model. The more an attribute is used to make key decisions with decision trees, the higher its relative importance. This importance is calculated explicitly for each attribute in the dataset, allowing attributes to be ranked and compared to each other.
Figure 3 shows the relative importance of features output by the XGBoost classifier. Lattice energy per atom, atom density, electronic energy band gap, mass density, and O/M ratio were the key descriptors identified as important by our classifier. The idea behind performing the classification step was to shortlist the promising candidates based on their crystal structure, compound chemistry and interatomic bonding in the initial process of material design without having to calculate any complex derived properties. Some of the descriptors identified by the classification algorithm are intuitive and known from the physics of heat conduction. For example, Lattice energy per atom is a measure of interatomic bonding in a material. The lower the
$ {e}_L $
, the higher the strength of interatomic bonding and higher the
$ {k}_L $
. Similarly, classification model also predicts the importance of atom density and mass density, which have been reported earlier as influencing parameters in lattice thermal conductivity (Juneja et al., Reference Juneja, Yumnam, Satsangi and Singh2019). Electronic energy band gap and O/M ratio are two parameters, which are not directly linked to the physics of thermal conductivity, but are recognized as important classifying parameters in our study. The role of these parameters needs to be investigated further using atomistic modeling methods.
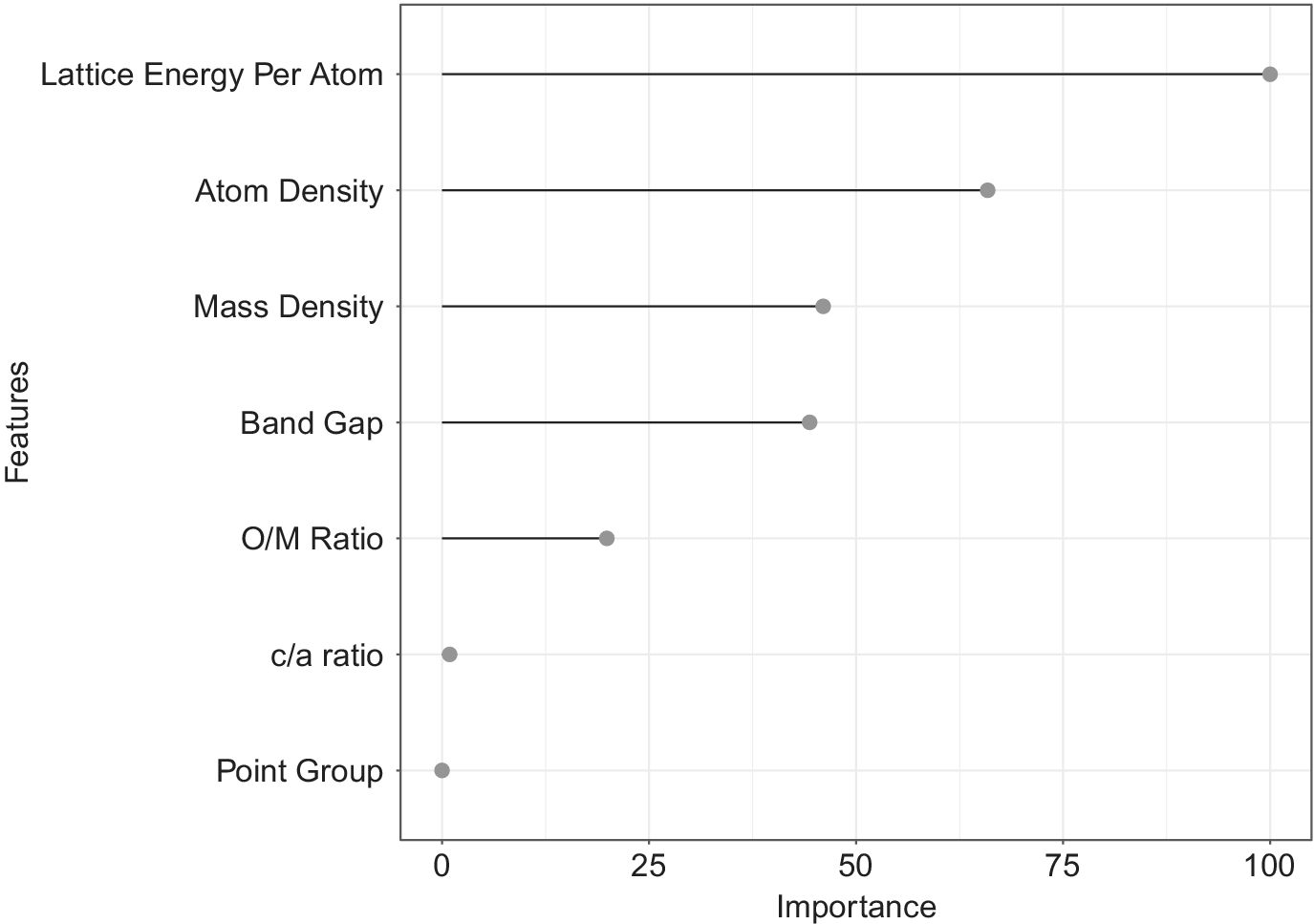
Figure 3. Feature importance plot generated by the XGBoost Classifier. The relative importance of descriptors is calculated by how useful it was while making key decisions with Decision Trees.
The second part of our formulated process, involved constructing regression-based predictive models. First, the regression models were built on the entire dataset, which was used for the classification. Random Forest models showed the highest accuracy with an cv – R
2 = 0.44 and cv − MAE = 3.2 on this dataset. The same model was then applied on already classified dataset of “low”
$ {k}_L $
values with the cv – R
2 = 0.70 and cv – MAE = 0.71. The performance of the random forest model on two different datasets is plotted in Figure 4 a,b. An improvement in the accuracy might be attributed to the narrower spread of the classified data. Classification helps reduce the variance in the dataset according to the range of the material property of interest, which is used in the regression step. It helps in achieving greater predictive accuracy even with small dataset in the regression step. To further improve the predictive accuracy, Debye temperature and Gruneisen parameter were added as descriptors in the list of descriptors used in the classification step. Best performance was achieved by cubist model giving the cv – R
2 = 0.96 and a cv – MAE = 0.19. Gaussian process regression with polynomial kernel and Kernel ridge regression also performed well giving an accuracy of cv – R
2 = 0.95, cv – MAE = 0.26 and cv – R
2 = 0.94, cv – MAE = 0.23, respectively. Details about the performance of other models is given in Table 3.
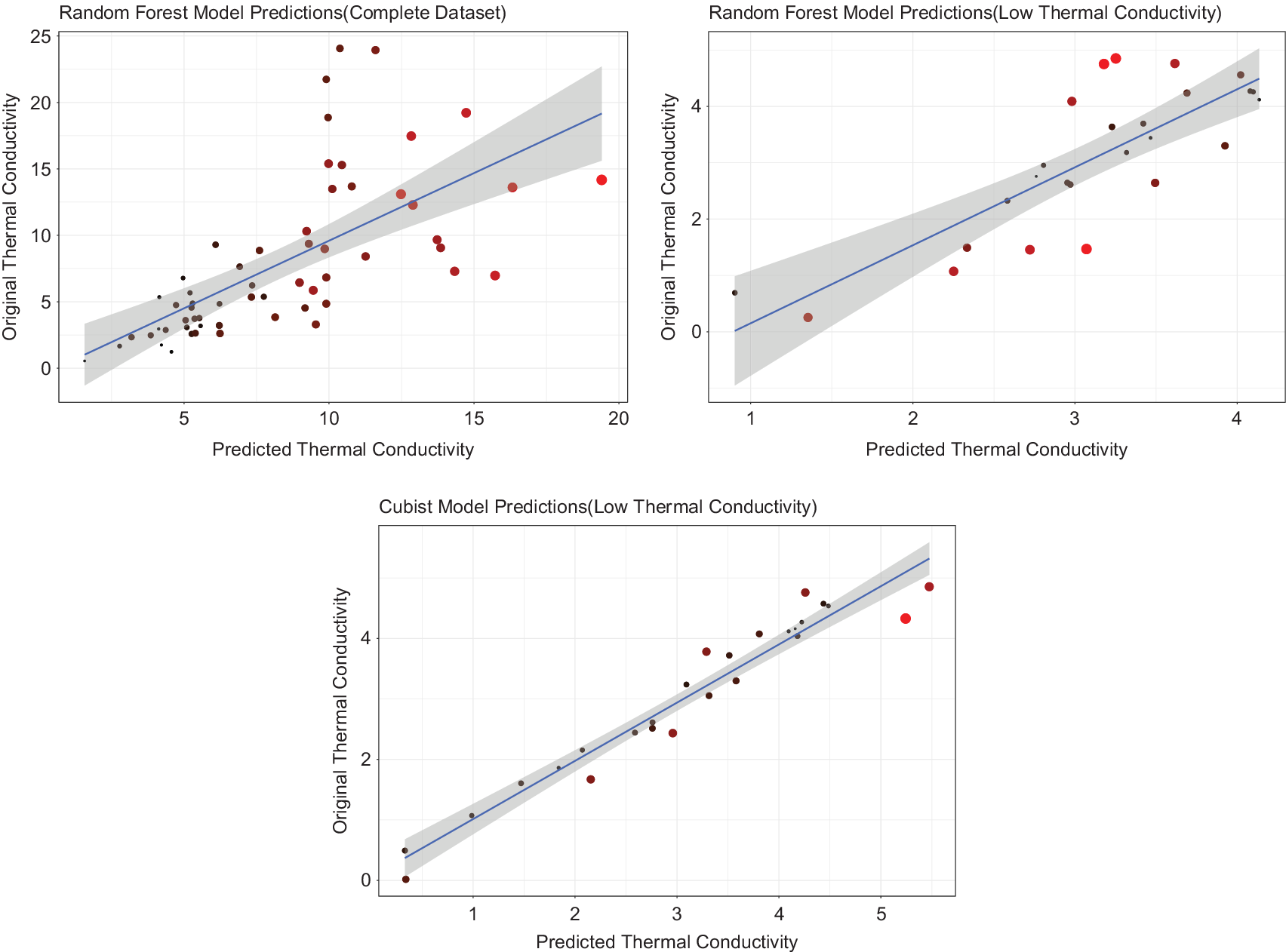
Figure 4. Predictions of the regression models where lighter shades of red and bigger point sizes represent higher residuals, (a) random forest fitted on entire dataset, (b) random forest fitted on dataset of low
$ {k}_L $
compounds, and (c) Cubist model fitted on low
$ {k}_L $
compounds including Debye temperature and Gruneisen parameter.
Table 3. Represents the 10-fold cross validation results obtained from the regression model including Gruneisen parameter and Debye temperature.
Cubist model achieves the best predictive power. The bad performance of Neural Networks is justified by the lack of training data.
Abbreviations: kNN, k Nearest Neighbors; RMSE, root mean square error; GBM, Gradient Boosted Machines; GPR, Gaussian Process Regression; MAE, mean absolute error.
It is to be noted that the classifier can be used independently of the regression step in cases when the values of Gruneisen parameter and Debye temperature are not available for the compound. This is useful when we have only limited information about the compound, that is only values for the fundamental material properties mentioned earlier. Another important point is that the feature importance identified by the classifier is only applicable when the classifier is used independently of the regression step. We claim this because the regression step uses a different model, which means that the same features might not turn out to be important for the regression step. Therefore, the regression step uses all descriptors used in the classification step in addition to using Gruneisen parameter and Debye temperature as descriptors.
Further, it was also observed that ML approaches in general work better than deep learning when applied to datasets related to material science. This can be attributed to the fact that neural networks need high amounts of data to approximate the underlying function (Hornik et al., Reference Hornik, Stinchcombe and White1989) representing the
$ {k}_L $
which is rarely available in cases of material science problems. Therefore, when a deep neural network with multiple permutations of the hidden layer (neurons) is built, it fails to converge to the optimal underlying function giving a large MAE of 2.14.
4 Conclusions
In this paper, a ML-based two-step process of discovering novel materials have been proposed. In the first step, classification is performed on the entire dataset to categorise the data, which is followed by fitting regression models to predict the numerical value of the property of interest. The proposed two-step process addresses the problem of small datasets in materials informatics by reducing the variance of the dataset using classification models according to the range of property of interest, which helps in achieving greater predictive accuracy in the regression step. The approach was applied on a dataset of transition metal oxides to classify and predict the
$ {k}_L $
values of low
$ {k}_L $
transition metal oxides. A high predictive accuracy of 95% was achieved using multiple ML-based regression algorithms, such as cubist model, kernel ridge and gaussian process. It was also shown that ML-based approach worked better in comparison to deep learning methods for problems involving small datasets. In addition, gradient boosted tree algorithm was able to identify key material properties namely: Lattice energy per atom, atom density, electronic energy band gap, mass density, and ratio of oxygen by transition metal atoms. Since the key descriptors can be derived from fundamental crystal structure, compound chemistry, and interatomic bonding, they can be easily utilized for the classification of compound in the early stages of materials selection, without needing to calculate computationally expensive derived complex properties. The two-step process proposed in the current work addresses a critical challenge in the materials informatics, which is the smaller sizes of datasets. The approach can be combined with high-throughput computing to discover novel materials for specific applications at lower computational cost. The work will be carried forward in that direction by demonstrating the proposed methodology on transition metal oxides to discover novel low
$ {k}_L $
oxides.
Funding Statement
This research was supported by grants from the Science and Engineering Research Board, India through project number SRG/2019/000644. In addition, S.P.A. Bordas received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 811099 TWINNING Project DRIVEN for the University of Luxembourg: \url{https://2020driven.uni.lu/}
Competing Interests
The authors declare no competing interests exist.
Authorship Contributions
Conceptualization, A.T.; Methodology, A.T., S.D., N.S., and S.B.; Data curation, S.D; Data visualisation, S.D.; Writing-original draft: A.T. and S.D. All authors approved the final submitted draft.
Data Availability Statement
Replication data and code can be found on the github repository for this project: \url{https://github.com/Sid-darthvader/Machine-Learning-for-Thermoelectrics-Discovery}.
Ethical Standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Supplementary Materials
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/dce.2020.7.
Open access
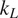
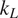
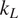
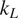
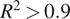
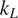
Comments
No Comments have been published for this article.