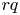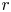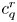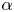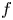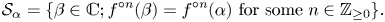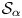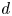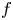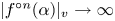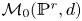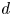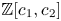Research Article
Equidistribution of Hodge loci II
- Part of:
-
- Published online by Cambridge University Press:
- 12 January 2023, pp. 1-52
-
- Article
- Export citation
Polynomial dynamics and local analysis of small and grand orbits
- Part of:
-
- Published online by Cambridge University Press:
- 12 January 2023, pp. 53-86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hofer–Zehnder conjecture on weighted projective spaces
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2023, pp. 87-108
-
- Article
- Export citation
Derived categories of hyper-Kähler manifolds: extended Mukai vector and integral structure
- Part of:
-
- Published online by Cambridge University Press:
- 31 January 2023, pp. 109-152
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative hyperbolicity of free-by-cyclic extensions
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2023, pp. 153-183
-
- Article
- Export citation
The integral Chow ring of
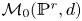 $\mathcal {M}_{0}(\mathbb {P}^r, d)$, for
$\mathcal {M}_{0}(\mathbb {P}^r, d)$, for 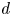 $d$ odd
$d$ odd
- Part of:
-
- Published online by Cambridge University Press:
- 31 January 2023, pp. 184-206
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 159 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 February 2023, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
COM volume 159 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 February 2023, pp. b1-b2
-
- Article
-
- You have access
- Export citation