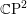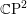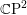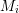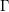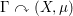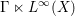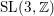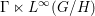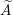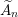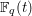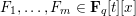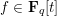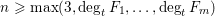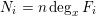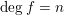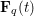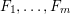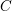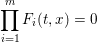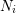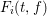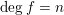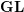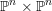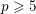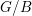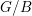Research Article
Ramification conjecture and Hirzebruch’s property of line arrangements
- Part of:
-
- Published online by Cambridge University Press:
- 25 October 2016, pp. 2443-2460
-
- Article
-
- You have access
- Export citation
Rigidity of free product von Neumann algebras
- Part of:
-
- Published online by Cambridge University Press:
- 17 November 2016, pp. 2461-2492
-
- Article
-
- You have access
- Export citation
A remark on fullness of some group measure space von Neumann algebras
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 2493-2502
-
- Article
-
- You have access
- Export citation
Affine Weyl group multiple Dirichlet series: type
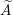 $\widetilde{A}$
$\widetilde{A}$
- Part of:
-
- Published online by Cambridge University Press:
- 08 November 2016, pp. 2503-2523
-
- Article
-
- You have access
- Export citation
On the Bateman–Horn conjecture for polynomials over large finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2525-2544
-
- Article
-
- You have access
- Export citation
Supernatural analogues of Beilinson monads
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2016, pp. 2545-2562
-
- Article
-
- You have access
- Export citation
Local models for Weil-restricted groups
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 2563-2601
-
- Article
-
- You have access
- Export citation
Chern–Schwartz–MacPherson classes for Schubert cells in flag manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2016, pp. 2603-2625
-
- Article
-
- You have access
- Export citation
The affine Grassmannian and the Springer resolution in positive characteristic
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2016, pp. 2627-2677
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 152 Issue 12 Cover and Front matter
-
- Published online by Cambridge University Press:
- 10 January 2017, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
COM volume 152 Issue 12 Cover and Back matter
-
- Published online by Cambridge University Press:
- 10 January 2017, pp. b1-b5
-
- Article
-
- You have access
- Export citation