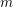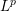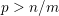Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Phong, Duong
Picard, Sebastien
and
Zhang, Xiangwen
2016.
A second order estimate for general complex Hessian equations.
Analysis & PDE,
Vol. 9,
Issue. 7,
p.
1693.
Phong, Duong H.
Picard, Sebastien
and
Zhang, Xiangwen
2017.
The Fu–Yau equation with negative slope parameter.
Inventiones mathematicae,
Vol. 209,
Issue. 2,
p.
541.
Chu, Jianchun
and
Zhou, Bin
2019.
Optimal regularity of plurisubharmonic envelopes on compact Hermitian manifolds.
Science China Mathematics,
Vol. 62,
Issue. 2,
p.
371.
Nguyen, Ngoc Cuong
2020.
On the Hölder continuous subsolution problem
for the complex Monge–Ampère equation, II.
Analysis & PDE,
Vol. 13,
Issue. 2,
p.
435.
Li, Chang
and
Shen, Liangming
2020.
The complex Hessian equations with gradient terms on Hermitian manifolds.
Journal of Differential Equations,
Vol. 269,
Issue. 7,
p.
6293.
Chu, Jianchun
and
McCleerey, Nicholas
2021.
Fully non-linear degenerate elliptic equations in complex geometry.
Journal of Functional Analysis,
Vol. 281,
Issue. 9,
p.
109176.
Feng, Xiaomeng
2021.
Solvability of the Neumann problem for complex hessian equations in balls.
Complex Variables and Elliptic Equations,
Vol. 66,
Issue. 3,
p.
361.
Kołodziej, Sławomir
and
Nguyen, Ngoc Cuong
2021.
Continuous solutions to Monge–Ampère equations on Hermitian manifolds for measures dominated by capacity.
Calculus of Variations and Partial Differential Equations,
Vol. 60,
Issue. 3,
Zhang, Dekai
2022.
Regularity of degenerate k-Hessian equations on closed Hermitian manifolds.
Advanced Nonlinear Studies,
Vol. 22,
Issue. 1,
p.
534.
Hai, Le Mau
and
Van Quan, Vu
2023.
Continuous Solutions to Complex Hessian Equations on Hermitian Manifolds.
The Journal of Geometric Analysis,
Vol. 33,
Issue. 12,
Sun, Wei
2024.
The weak solutions to complex Hessian equations.
Calculus of Variations and Partial Differential Equations,
Vol. 63,
Issue. 2,