Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T08:51:38.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Orderability and the Weinstein conjecture

Part of: Symplectic geometry, contact geometry Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems

Published online by Cambridge University Press:  24 September 2015

Peter Albers ,
Urs Fuchs  and
Will J. Merry
Peter Albers
Affiliation:
Mathematisches Institut, Westfälische Wilhelms-Universität Münster, Germany email peter.albers@wwu.de
Urs Fuchs
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, Germany email urs.fuchs@rub.de
Will J. Merry
Affiliation:
Department of Mathematics, ETH Zürich, Switzerland email merry@math.ethz.ch
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article we prove that the Weinstein conjecture holds for contact manifolds 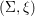$({\rm\Sigma},{\it\xi})$ for which 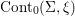$\text{Cont}_{0}({\rm\Sigma},{\it\xi})$ is non-orderable in the sense of Eliashberg and Polterovich [Partially ordered groups and geometry of contact transformations, Geom. Funct. Anal. 10 (2000), 1448–1476]. More precisely, we establish a link between orderable and hypertight contact manifolds. In addition, we prove for certain contact manifolds a conjecture by Sandon [A Morse estimate for translated points of contactomorphisms of spheres and projective spaces, Geom. Dedicata 165 (2013), 95–110] on the existence of translated points in the non-degenerate case.

Keywords

orderabilityWeinstein conjecturehypertight contact structuresRabinowitz Floer homology

MSC classification

Primary: 37J55: Contact systems 53D10: Contact manifolds, general 53D40: Floer homology and cohomology, symplectic aspects 53D42: Symplectic field theory; contact homology
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 12 , December 2015 , pp. 2251 - 2272
Copyright
© The Authors 2015 

References

Ahlfors, L., Confomal invariants: topics in geometric function theory (McGraw-Hill, New York, Düsseldorf, Johannesburg, 1973).Google Scholar
Albers, P. and Frauenfelder, U., Leaf-wise intersections and Rabinowitz Floer homology, J. Topol. Anal. 2 (2010), 77–98.CrossRefGoogle Scholar
Albers, P. and Merry, W. J., Translated points and Rabinowitz Floer homology, J. Fixed Point Theory Appl. 13 (2013), 201–214.CrossRefGoogle Scholar
Bourgeois, F., Eliashberg, Y., Hofer, H., Wysocki, K. and Zehnder, E., Compactness results in symplectic field theory, Geom. Topol. 7 (2003), 799–888.CrossRefGoogle Scholar
Cieliebak, K. and Frauenfelder, U., A Floer homology for exact contact embeddings, Pacific J. Math. 239 (2009), 216–251.CrossRefGoogle Scholar
Cieliebak, K. and Mohnke, K., Compactness for punctured holomorphic curves. Conference on Symplectic Topology, J. Symplectic Geom. 3 (2005), 589–654.CrossRefGoogle Scholar
Colin, V. and Honda, K., Constructions contrôlées de champs de Reeb et applications, Geom. Topol. 9 (2005), 2193–2226.CrossRefGoogle Scholar
Eliashberg, Y., Hofer, H. and Salamon, D. A., Lagrangian intersections in contact geometry, Geom. Funct. Anal. 5 (1995), 244–269.CrossRefGoogle Scholar
Eliashberg, Y., Kim, S. S. and Polterovich, L., Geometry of contact transformations and domains: orderability versus squeezing, Geom. Topol. 10 (2006), 1635–1747.CrossRefGoogle Scholar
Eliashberg, Y. and Polterovich, L., Partially ordered groups and geometry of contact transformations, Geom. Funct. Anal. 10 (2000), 1448–1476.CrossRefGoogle Scholar
Fish, J., Compactness Results for Pseudo-holomorphic curves, PhD thesis, New York University, September (2007).Google Scholar
Fish, J., Target-local Gromov compactness, Geom. Topol. 15 (2011), 765–826.CrossRefGoogle Scholar
Geiges, H., An introduction to contact topology, Cambridge Studies in Advanced Mathematics, vol. 109 (Cambridge University Press, Cambridge, 2008).CrossRefGoogle Scholar
Gromov, M., Filling Riemannian manifolds, J. Differential Geom. 18 (1983), 1–147.CrossRefGoogle Scholar
Hofer, H., Pseudoholomorphic curves in symplectizations with applications to the Weinstein conjecture in dimension three, Invent. Math. 114 (1993), 515–563.CrossRefGoogle Scholar
Hofer, H., Wysocki, C. and Zehnder, E., Finite energy cylinders of small area, Ergodic Theory Dynam. Systems 22 (2002), 1451–1486.CrossRefGoogle Scholar
Hummel, C., Gromov’s compactness theorem for pseudo-holomorphic curves, Progress in Mathematics, vol. 151 (Birkhäuser, Basel, 1997).CrossRefGoogle Scholar
Hutchings, M., Taubes’s proof of the Weinstein conjecture in dimension three, Bull. Amer. Math. Soc. (N.S.) 47 (2010), 73–125.CrossRefGoogle Scholar
Laudenbach, F., Orbites périodiques et courbes pseudo-holomorphes, application à la conjecture de Weinstein en dimension 3 (d’après H. Hofer et al.), Astérisque 227 (1995), 309–333.Google Scholar
McDuff, D. and Salamon, D., Introduction to symplectic topology, Oxford Mathematical Monographs, second edition (Oxford University Press, New York, 1998).Google Scholar
Sandon, S., Contact homology, capacity and non-squeezing in ℝ2n × S 1 via generating functions, Ann. Inst. Fourier (Grenoble) 61 (2011), 145–185.CrossRefGoogle Scholar
Sandon, S., On iterated translated points for contactomorphisms of ℝ2n+1 and ℝ2n × S 1, Internat. J. Math. 23(2) (2012), 1250042.CrossRefGoogle Scholar
Sandon, S., A Morse estimate for translated points of contactomorphisms of spheres and projective spaces, Geom. Dedicata 165 (2013), 95–110.CrossRefGoogle Scholar
Schwarz, M., On the action spectrum for closed symplectically aspherical manifolds, Pacific J. Math. 193 (2000), 419–461.CrossRefGoogle Scholar
Weinstein, A., On the hypotheses of Rabinowitz’ periodic orbit theorems, J. Differential Equations 33 (1979), 353–358.CrossRefGoogle Scholar