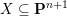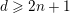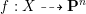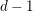Introduction
There has been a great deal of recent interest and progress in studying issues of rationality for algebraic varieties (cf. [Reference KollárKol95, Reference VoisinVoi15, Reference VoisinVoi14, Reference TotaroTot16, Reference Hassett, Pirutka and TschinkelHPT16]). The purpose of this paper is to investigate a complementary circle of questions: in what manner can one quantify and control ‘how irrational’ a given projective variety
![]() $X$
might be? We consider various measures of irrationality for hypersurfaces of large degree in projective space and other varieties. The theme is that positivity properties of canonical bundles lead to lower bounds for these invariants. In particular, we prove the main conjecture of [Reference Bastianelli, Cortini and De PoiBCDP14] that if
$X$
might be? We consider various measures of irrationality for hypersurfaces of large degree in projective space and other varieties. The theme is that positivity properties of canonical bundles lead to lower bounds for these invariants. In particular, we prove the main conjecture of [Reference Bastianelli, Cortini and De PoiBCDP14] that if
![]() $X\subseteq \mathbf{P}^{n+1}$
is a very general smooth hypersurface of dimension
$X\subseteq \mathbf{P}^{n+1}$
is a very general smooth hypersurface of dimension
![]() $n$
and degree
$n$
and degree
![]() $d\geqslant 2n+1$
, then any dominant rational mapping
$d\geqslant 2n+1$
, then any dominant rational mapping
![]() $f:X{\dashrightarrow}\mathbf{P}^{n}$
must satisfy
$f:X{\dashrightarrow}\mathbf{P}^{n}$
must satisfy
We also propose a number of open problems involving this circle of ideas, and we show how our methods lead to simple new proofs of theorems of Ran [Reference RanRan91] and Beheshti and Eisenbud [Reference Beheshti and EisenbudBE10] concerning varieties of multi-secant lines.
To start with some background, recall that the gonality
![]() $\operatorname{gon}(C)$
of an irreducible complex projective curve
$\operatorname{gon}(C)$
of an irreducible complex projective curve
![]() $C$
is defined to be the least degree of a branched covering
$C$
is defined to be the least degree of a branched covering
where
![]() $C^{\prime }$
is the normalization of
$C^{\prime }$
is the normalization of
![]() $C$
. Thus
$C$
. Thus
and it is profitable in general to view
![]() $\operatorname{gon}(C)$
as measuring the failure of
$\operatorname{gon}(C)$
as measuring the failure of
![]() $C$
to be rational. Because of this there has been a certain amount of interest over the years in bounding from below the gonality of various natural classes of curves. For instance, a classical theorem of Noether states that if
$C$
to be rational. Because of this there has been a certain amount of interest over the years in bounding from below the gonality of various natural classes of curves. For instance, a classical theorem of Noether states that if
![]() $C\subseteq \mathbf{P}^{2}$
is a smooth plane curve of degree
$C\subseteq \mathbf{P}^{2}$
is a smooth plane curve of degree
![]() $d\geqslant 3$
, then
$d\geqslant 3$
, then
with the relevant coverings given by projection from a point of
![]() $C$
. This was generalized to complete intersection and other curves in [Reference LazarsfeldLaz97, Example 4.12] and [Reference Hartshorne and SchlesingerHS11] by means of vector bundle techniques. Abramovich [Reference AbramovichAbr96] used results of Li and Yau to obtain a linear lower bound on the gonality of modular curves. In a somewhat different direction, it was established in [Reference LazarsfeldLaz96] that the Buser–Sarnak invariant of
$C$
. This was generalized to complete intersection and other curves in [Reference LazarsfeldLaz97, Example 4.12] and [Reference Hartshorne and SchlesingerHS11] by means of vector bundle techniques. Abramovich [Reference AbramovichAbr96] used results of Li and Yau to obtain a linear lower bound on the gonality of modular curves. In a somewhat different direction, it was established in [Reference LazarsfeldLaz96] that the Buser–Sarnak invariant of
![]() $\text{Jac}(C)$
is linearly bounded above by
$\text{Jac}(C)$
is linearly bounded above by
![]() $\operatorname{gon}(C)$
, and the behavior of gonality in certain towers of coverings was studied by Hwang and To [Reference Hwang and ToHT12] as a consequence of relations they established between gonality and injectivity radii. The paper [Reference Bakker and TsimermanBT13] contains some interesting applications of the results of Hwang–To.
$\operatorname{gon}(C)$
, and the behavior of gonality in certain towers of coverings was studied by Hwang and To [Reference Hwang and ToHT12] as a consequence of relations they established between gonality and injectivity radii. The paper [Reference Bakker and TsimermanBT13] contains some interesting applications of the results of Hwang–To.
Several authors have proposed and studied some analogous measures of irrationality for an irreducible complex projective variety
![]() $X$
of arbitrary dimension
$X$
of arbitrary dimension
![]() $n$
. We will be principally concerned here with three of these, the degree of irrationality, the connecting gonality, and the covering gonality of
$n$
. We will be principally concerned here with three of these, the degree of irrationality, the connecting gonality, and the covering gonality of
![]() $X$
, defined as follows:
$X$
, defined as follows:
 $$\begin{eqnarray}\displaystyle \operatorname{irr}(X) & = & \displaystyle \min \left\{\unicode[STIX]{x1D6FF}>0\biggm\vert\begin{array}{@{}c@{}}\exists \text{degree }\unicode[STIX]{x1D6FF}\text{ rational covering}\\ X{\dashrightarrow}\mathbf{P}^{n}\end{array}\right\};\nonumber\\ \displaystyle \operatorname{conn.gon}(X) & = & \displaystyle \min \left\{c>0\left|\begin{array}{@{}c@{}}\text{General points }x,y\in X\text{ can be}\\ \text{connected by an irreducible curve}\\ C\subseteq X\text{ with }\operatorname{gon}(C)=c\end{array}\right.\right\};\nonumber\\ \displaystyle \operatorname{cov.gon}(X) & = & \displaystyle \min \left\{c>0\left|\begin{array}{@{}c@{}}\text{Given a general point }x\in X,\exists \text{an}\\ \text{ irreducible curve }C\subseteq X\text{ through }x\text{ with}\\ \operatorname{gon}(C)=c\end{array}\right.\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{irr}(X) & = & \displaystyle \min \left\{\unicode[STIX]{x1D6FF}>0\biggm\vert\begin{array}{@{}c@{}}\exists \text{degree }\unicode[STIX]{x1D6FF}\text{ rational covering}\\ X{\dashrightarrow}\mathbf{P}^{n}\end{array}\right\};\nonumber\\ \displaystyle \operatorname{conn.gon}(X) & = & \displaystyle \min \left\{c>0\left|\begin{array}{@{}c@{}}\text{General points }x,y\in X\text{ can be}\\ \text{connected by an irreducible curve}\\ C\subseteq X\text{ with }\operatorname{gon}(C)=c\end{array}\right.\right\};\nonumber\\ \displaystyle \operatorname{cov.gon}(X) & = & \displaystyle \min \left\{c>0\left|\begin{array}{@{}c@{}}\text{Given a general point }x\in X,\exists \text{an}\\ \text{ irreducible curve }C\subseteq X\text{ through }x\text{ with}\\ \operatorname{gon}(C)=c\end{array}\right.\right\}.\nonumber\end{eqnarray}$$
(Note that the curves
![]() $C$
computing the connecting and covering gonalities are allowed to be singular.) Thus
$C$
computing the connecting and covering gonalities are allowed to be singular.) Thus
 $$\begin{eqnarray}\displaystyle \operatorname{irr}(X)=1 & \Longleftrightarrow & \displaystyle X\text{ is rational},\nonumber\\ \displaystyle \operatorname{conn.gon}(X)=1 & \Longleftrightarrow & \displaystyle X\text{ is rationally connected},\nonumber\\ \displaystyle \operatorname{cov.gon}(X)=1 & \Longleftrightarrow & \displaystyle X\text{ is uniruled},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{irr}(X)=1 & \Longleftrightarrow & \displaystyle X\text{ is rational},\nonumber\\ \displaystyle \operatorname{conn.gon}(X)=1 & \Longleftrightarrow & \displaystyle X\text{ is rationally connected},\nonumber\\ \displaystyle \operatorname{cov.gon}(X)=1 & \Longleftrightarrow & \displaystyle X\text{ is uniruled},\nonumber\end{eqnarray}$$
and in general one has the inequalities
The integer
![]() $\operatorname{irr}(X)$
is perhaps the most natural generalization of the gonality of a curve, but
$\operatorname{irr}(X)$
is perhaps the most natural generalization of the gonality of a curve, but
![]() $\operatorname{cov.gon}(X)$
often seems to be easier to control.Footnote
1
Another invariant, suggested by Voisin, is the least degree
$\operatorname{cov.gon}(X)$
often seems to be easier to control.Footnote
1
Another invariant, suggested by Voisin, is the least degree
![]() $v(X)$
of one-parameter families of Chow-constant zero-cycles that cover
$v(X)$
of one-parameter families of Chow-constant zero-cycles that cover
![]() $X$
. This satisfies
$X$
. This satisfies
![]() $v(X)\leqslant \operatorname{cov.gon}(X)$
.
$v(X)\leqslant \operatorname{cov.gon}(X)$
.
The degree of irrationality was introduced by Heinzer and Moh in [Reference Heinzer and MohHM82], and Yoshihara subsequently computed it for several classes of surfaces [Reference YoshiharaYos94, Reference Tokunaga and YoshiharaTY95, Reference YoshiharaYos00, Reference YoshiharaYos98, Reference YoshiharaYos96]. Lopez and Pirola [Reference Lopez and PirolaLP95] showed in passing that if
![]() $X\subseteq \mathbf{P}^{3}$
is a surface of degree
$X\subseteq \mathbf{P}^{3}$
is a surface of degree
![]() $d\geqslant 4$
, then
$d\geqslant 4$
, then
![]() $\operatorname{cov.gon}(X)=d-2$
. Along similar lines, Fakhruddin established in his note [Reference FakhruddinFak02] that given any integer
$\operatorname{cov.gon}(X)=d-2$
. Along similar lines, Fakhruddin established in his note [Reference FakhruddinFak02] that given any integer
![]() $c>0$
, a very general hypersurface of sufficiently large degree in any smooth variety does not contain any curves of gonality less than or equal to
$c>0$
, a very general hypersurface of sufficiently large degree in any smooth variety does not contain any curves of gonality less than or equal to
![]() $c$
. However, as a measure of irrationality, it seems that the covering gonality was first studied systematically in [Reference BastianelliBas12], where the first author computes
$c$
. However, as a measure of irrationality, it seems that the covering gonality was first studied systematically in [Reference BastianelliBas12], where the first author computes
![]() $\operatorname{cov.gon}(X)$
and bounds
$\operatorname{cov.gon}(X)$
and bounds
![]() $\operatorname{irr}(X)$
when
$\operatorname{irr}(X)$
when
![]() $X=C_{2}$
is the symmetric square of a curve
$X=C_{2}$
is the symmetric square of a curve
![]() $C$
.
$C$
.
The present work was most directly motivated by the paper [Reference Bastianelli, Cortini and De PoiBCDP14] in which Cortini and the first two authors consider the question of computing the degree of irrationality of a smooth projective hypersurface
of degree
![]() $d$
and dimension
$d$
and dimension
![]() $n\geqslant 2$
, generalizing the result of Noether for plane curves cited above. They show to begin with that if
$n\geqslant 2$
, generalizing the result of Noether for plane curves cited above. They show to begin with that if
![]() $d\geqslant n+3$
, then
$d\geqslant n+3$
, then
It can happen that
![]() $\operatorname{irr}(X)<d-1$
, but it was established in [Reference Bastianelli, Cortini and De PoiBCDP14] that if
$\operatorname{irr}(X)<d-1$
, but it was established in [Reference Bastianelli, Cortini and De PoiBCDP14] that if
![]() $X$
is a very general surface of degree
$X$
is a very general surface of degree
![]() $d\geqslant 5$
or threefold of degree
$d\geqslant 5$
or threefold of degree
![]() $d\geqslant 7$
, then
$d\geqslant 7$
, then
and the exceptional cases were classified in these dimensions. It was conjectured there that this statement extends to hypersurfaces of all dimensions.
Our first results concern covering gonality.
Theorem A. Let
![]() $X\subseteq \mathbf{P}^{n+1}$
be a smooth hypersurface of dimension
$X\subseteq \mathbf{P}^{n+1}$
be a smooth hypersurface of dimension
![]() $n$
and degree
$n$
and degree
![]() $d\geqslant n+2$
. Then
$d\geqslant n+2$
. Then
More generally, we show that
![]() $v(X)\geqslant d-n$
. Observe that one recovers, in particular, the lower bound (2) of Bastianelli, Cortini and De Poi on the degree of irrationality of such hypersurfaces. In fact it suffices in the theorem that
$v(X)\geqslant d-n$
. Observe that one recovers, in particular, the lower bound (2) of Bastianelli, Cortini and De Poi on the degree of irrationality of such hypersurfaces. In fact it suffices in the theorem that
![]() $X$
is normal with at worst canonical singularities, and in this setting the statement is best possible for every
$X$
is normal with at worst canonical singularities, and in this setting the statement is best possible for every
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
![]() $d\geqslant n+2$
. On the other hand, the covering gonality of a smooth hypersurface
$d\geqslant n+2$
. On the other hand, the covering gonality of a smooth hypersurface
![]() $X$
can be bounded from above by considering families of singular plane curves covering
$X$
can be bounded from above by considering families of singular plane curves covering
![]() $X$
(cf. Example 1.7 and Remark 1.8).
$X$
(cf. Example 1.7 and Remark 1.8).
We actually prove that the conclusion of the theorem and the bound for
![]() $v(X)$
hold for any smooth projective variety
$v(X)$
hold for any smooth projective variety
![]() $X$
with
$X$
with
where
![]() $B$
is a
$B$
is a
![]() $(d-n-2)$
-very ample divisor on
$(d-n-2)$
-very ample divisor on
![]() $X$
and
$X$
and
![]() $E$
is effective.Footnote
2
Thus we deduce the following.
$E$
is effective.Footnote
2
Thus we deduce the following.
Corollary B. Let
![]() $M$
be a smooth projective variety, and let
$M$
be a smooth projective variety, and let
![]() $A$
be a very ample divisor on
$A$
be a very ample divisor on
![]() $M$
. There is an integer
$M$
. There is an integer
![]() $e=e(M,A)$
depending only on
$e=e(M,A)$
depending only on
![]() $M$
and
$M$
and
![]() $A$
with the property that if
$A$
with the property that if
is any smooth divisor, then
In particular, the degree of irrationality of
![]() $X_{d}$
goes to infinity with
$X_{d}$
goes to infinity with
![]() $d$
. (One can prove this last fact directly using the ideas of [Reference Lopez and PirolaLP95, Reference BastianelliBas12, Reference Bastianelli, Cortini and De PoiBCDP14, Reference Guerra and PirolaGP08]: see Remark 3.2.) As noted above, Fakhruddin proved in [Reference FakhruddinFak02] the closely related result that in the situation of the Corollary, there is a linear function
$d$
. (One can prove this last fact directly using the ideas of [Reference Lopez and PirolaLP95, Reference BastianelliBas12, Reference Bastianelli, Cortini and De PoiBCDP14, Reference Guerra and PirolaGP08]: see Remark 3.2.) As noted above, Fakhruddin proved in [Reference FakhruddinFak02] the closely related result that in the situation of the Corollary, there is a linear function
![]() $d(c)$
such that a very general divisor
$d(c)$
such that a very general divisor
![]() $X_{d}\in |dA|$
actually contains no curves of gonality less than or equal to
$X_{d}\in |dA|$
actually contains no curves of gonality less than or equal to
![]() $c$
provided that
$c$
provided that
![]() $d\geqslant d(c)$
. (Compare Proposition 3.8 below.)
$d\geqslant d(c)$
. (Compare Proposition 3.8 below.)
Returning to smooth hypersurfaces in projective space, our second theorem proves the main conjecture of [Reference Bastianelli, Cortini and De PoiBCDP14].
Theorem C. Let
![]() $X\subseteq \mathbf{P}^{n+1}$
be a very general smooth hypersurface of dimension
$X\subseteq \mathbf{P}^{n+1}$
be a very general smooth hypersurface of dimension
![]() $n$
and degree
$n$
and degree
![]() $d\geqslant 2n+1$
. Then
$d\geqslant 2n+1$
. Then
Furthermore, if
![]() $d\geqslant 2n+2$
, then any rational mapping
$d\geqslant 2n+2$
, then any rational mapping
is given by projection from a point of
![]() $X$
.
$X$
.
The proof of Theorem A, which is quite quick and elementary, occupies § 1: there we work on an arbitrary smooth variety whose canonical bundle satisfies a suitable positivity property. Voisin’s invariant
![]() $v(X)$
is studied in § 2 using the ideas introduced by Mumford in [Reference MumfordMum69]. These results actually imply Theorem 1.10, but we felt that it was worthwhile nonetheless to present the elementary and transparent proof of that statement.
$v(X)$
is studied in § 2 using the ideas introduced by Mumford in [Reference MumfordMum69]. These results actually imply Theorem 1.10, but we felt that it was worthwhile nonetheless to present the elementary and transparent proof of that statement.
For Theorem C, which appears in § 3, we start with the set-up established in [Reference Bastianelli, Cortini and De PoiBCDP14]. It is shown there that if
is a rational mapping with
then each of the fibres of
![]() $f$
spans a line in
$f$
spans a line in
![]() $\mathbf{P}^{n+1}$
provided that
$\mathbf{P}^{n+1}$
provided that
![]() $d\geqslant 2n+1$
. Furthermore these lines form a congruence of order one on
$d\geqslant 2n+1$
. Furthermore these lines form a congruence of order one on
![]() $\mathbf{P}^{n+1}$
, meaning that a general point of
$\mathbf{P}^{n+1}$
, meaning that a general point of
![]() $\mathbf{P}^{n+1}$
lies on exactly one of the lines. The main effort in [Reference Bastianelli, Cortini and De PoiBCDP14] was to use results on the classification of such congruences to show that
$\mathbf{P}^{n+1}$
lies on exactly one of the lines. The main effort in [Reference Bastianelli, Cortini and De PoiBCDP14] was to use results on the classification of such congruences to show that
![]() $X$
must contain a rational curve when
$X$
must contain a rational curve when
![]() $n=2$
or
$n=2$
or
![]() $n=3$
, which forces
$n=3$
, which forces
![]() $X$
to be special provided that
$X$
to be special provided that
![]() $d\geqslant 2n+1$
. The new point here is the observation that in arbitrary dimension
$d\geqslant 2n+1$
. The new point here is the observation that in arbitrary dimension
![]() $n$
, whether or not
$n$
, whether or not
![]() $X$
contains a rational curve, one can locate on
$X$
contains a rational curve, one can locate on
![]() $X$
a relatively large subvariety covered by curves of gonality
$X$
a relatively large subvariety covered by curves of gonality
![]() $e\leqslant n$
. On the other hand, drawing on computations of the third author and Voisin in [Reference EinEin88, Reference VoisinVoi96], one can bound the dimension of a subvariety of small covering gonality in a very general hypersurface. Theorem C follows. The common thread in these arguments is that the invariants we consider are ultimately controlled by measuring the positivity of canonical bundles.
$e\leqslant n$
. On the other hand, drawing on computations of the third author and Voisin in [Reference EinEin88, Reference VoisinVoi96], one can bound the dimension of a subvariety of small covering gonality in a very general hypersurface. Theorem C follows. The common thread in these arguments is that the invariants we consider are ultimately controlled by measuring the positivity of canonical bundles.
In § 4 we present a number of conjectures and open problems. It turns out that the computations in § 3 also lead to quick new proofs of results of Ran [Reference RanRan91] and Beheshti and Eisenbud [Reference Beheshti and EisenbudBE10] concerning varieties with many highly secant lines. These appear in Appendix A.
The reader will see that the methods of the present paper are rather elementary, and several of the ideas involved are at least implicit in earlier work such as [Reference Lopez and PirolaLP95, Reference FakhruddinFak02, Reference KnutsenKnu01, Reference BastianelliBas12, Reference Bastianelli, Cortini and De PoiBCDP14, Reference Guerra and PirolaGP08]. However, we have tried to pull things together in a natural way by focusing on a specific birational measure of positivity for the canonical bundle (Definition 1.1). We hope that this might help to lay the foundation for further work on what we consider to be an interesting circle of questions.
In an earlier version of this paper, the last three authors proved the conjecture of [Reference Bastianelli, Cortini and De PoiBCDP14] under the stronger numerical hypothesis
![]() $d\geqslant 3n$
, which the first two authors weakened somewhat in an appendix. Voisin subsequently showed us how to get this down to
$d\geqslant 3n$
, which the first two authors weakened somewhat in an appendix. Voisin subsequently showed us how to get this down to
![]() $d>\frac{5}{2}n$
, after which the first two authors were able to prove Theorem C as stated above.Footnote
3
The present paper represents a pooling of these efforts.
$d>\frac{5}{2}n$
, after which the first two authors were able to prove Theorem C as stated above.Footnote
3
The present paper represents a pooling of these efforts.
We are honored to dedicate this paper to János Kollár on the occasion of his sixtieth birthday. Beyond guiding the direction of algebraic geometry over three decades, János has been instrumental to the work of the third and fourth authors through his encouragement and generosity with ideas. It is a pleasure to have this opportunity to express our admiration and thanks.
Concerning notation and conventions, we work throughout over the complex numbers. As usual, morphisms are indicated by solid arrows, while rational mappings are dashed. We have taken the customary liberties in confounding line bundles and divisors.
1 Birational positivity and covering gonality
In this section we study the covering gonality of a projective variety
![]() $X$
, and prove Theorem A from the Introduction. The basic strategy is to bound
$X$
, and prove Theorem A from the Introduction. The basic strategy is to bound
![]() $\operatorname{cov.gon}(X)$
in terms of the positivity of the canonical bundle
$\operatorname{cov.gon}(X)$
in terms of the positivity of the canonical bundle
![]() $K_{X}$
. So we start with some remarks on birational measures of positivity for line bundles.
$K_{X}$
. So we start with some remarks on birational measures of positivity for line bundles.
Let
![]() $X$
be an irreducible projective variety. Given an integer
$X$
be an irreducible projective variety. Given an integer
![]() $p\geqslant 0$
, recall that a line bundle
$p\geqslant 0$
, recall that a line bundle
![]() $L$
on
$L$
on
![]() $X$
is said to be
$X$
is said to be
![]() $p$
-very ample if the restriction map
$p$
-very ample if the restriction map
is surjective for every finite subscheme
![]() $\unicode[STIX]{x1D709}\subseteq X$
of length
$\unicode[STIX]{x1D709}\subseteq X$
of length
![]() $p+1$
. In other words, one asks that every subscheme of length
$p+1$
. In other words, one asks that every subscheme of length
![]() $p+1$
imposes independent conditions on the sections of
$p+1$
imposes independent conditions on the sections of
![]() $L$
. The condition we focus on here is a birational analogue of this.
$L$
. The condition we focus on here is a birational analogue of this.
Definition 1.1. A line bundle
![]() $L$
on
$L$
on
![]() $X$
satisfies property
$X$
satisfies property
![]() $\operatorname{(BVA)}_{p}$
if there exists a proper Zariski-closed subset
$\operatorname{(BVA)}_{p}$
if there exists a proper Zariski-closed subset
![]() $Z=Z(L)\subsetneq X$
depending on
$Z=Z(L)\subsetneq X$
depending on
![]() $L$
such that
$L$
such that
surjects for every finite subscheme
![]() $\unicode[STIX]{x1D709}\subset X$
of length
$\unicode[STIX]{x1D709}\subset X$
of length
![]() $p+1$
whose support is disjoint from
$p+1$
whose support is disjoint from
![]() $Z$
.
$Z$
.
Thus
![]() $\operatorname{(BVA)}_{0}$
is equivalent to requiring that
$\operatorname{(BVA)}_{0}$
is equivalent to requiring that
![]() $L$
be effective, and
$L$
be effective, and
![]() $\operatorname{(BVA)}_{1}$
is what is often called ‘birationally very ample’.Footnote
4
This property was considered in [Reference KnutsenKnu01, Reference Knutsen, Syzdek and SzembergKSS09] (under a different name).
$\operatorname{(BVA)}_{1}$
is what is often called ‘birationally very ample’.Footnote
4
This property was considered in [Reference KnutsenKnu01, Reference Knutsen, Syzdek and SzembergKSS09] (under a different name).
The following remarks yield a supply of examples.
Example 1.2. Let
![]() $X$
be an irreducible projective variety.
$X$
be an irreducible projective variety.
-
(i) If
 $L$
is a line bundle on
$L$
is a line bundle on
 $X$
satisfying
$X$
satisfying
 $\operatorname{(BVA)}_{p}$
and
$\operatorname{(BVA)}_{p}$
and
 $E$
is an effective divisor on
$E$
is an effective divisor on
 $X$
, then
$X$
, then
 ${\mathcal{O}}_{X}(L+E)$
satisfies
${\mathcal{O}}_{X}(L+E)$
satisfies
 $\operatorname{(BVA)}_{p}$
.
$\operatorname{(BVA)}_{p}$
. -
(ii) Suppose that
 $f:X\longrightarrow Y$
is a birational morphism of irreducible projective varieties. If
$f:X\longrightarrow Y$
is a birational morphism of irreducible projective varieties. If
 $L$
is a line bundle on
$L$
is a line bundle on
 $Y$
satisfying
$Y$
satisfying
 $\operatorname{(BVA)}_{p}$
, then
$\operatorname{(BVA)}_{p}$
, then
 $f^{\ast }L$
satisfies
$f^{\ast }L$
satisfies
 $\operatorname{(BVA)}_{p}$
on
$\operatorname{(BVA)}_{p}$
on
 $X$
.
$X$
. -
(iii) More generally, let
 $f:X\longrightarrow Y$
be a morphism which is birational onto its image, and suppose that
$f:X\longrightarrow Y$
be a morphism which is birational onto its image, and suppose that
 $L$
satisfies
$L$
satisfies
 $\operatorname{(BVA)}_{p}$
on
$\operatorname{(BVA)}_{p}$
on
 $Y$
. Assume moreover that
$Y$
. Assume moreover that
 $f(X)$
is not contained in the exceptional set
$f(X)$
is not contained in the exceptional set
 $Z\subseteq Y$
arising in the definition of property
$Z\subseteq Y$
arising in the definition of property
 $\operatorname{(BVA)}_{}$
. Then
$\operatorname{(BVA)}_{}$
. Then
 $f^{\ast }L$
satisfies
$f^{\ast }L$
satisfies
 $\operatorname{(BVA)}_{p}$
on
$\operatorname{(BVA)}_{p}$
on
 $X$
.
$X$
. -
(iv) Suppose that
is a morphism from $$\begin{eqnarray}f:X\longrightarrow \mathbf{P}\end{eqnarray}$$
$$\begin{eqnarray}f:X\longrightarrow \mathbf{P}\end{eqnarray}$$
 $X$
to some projective space which is birational onto its image. Then
$X$
to some projective space which is birational onto its image. Then
 $f^{\ast }{\mathcal{O}}_{\mathbf{P}}(p)$
satisfies
$f^{\ast }{\mathcal{O}}_{\mathbf{P}}(p)$
satisfies
 $\operatorname{(BVA)}_{p}$
.
$\operatorname{(BVA)}_{p}$
.
-
(v) Suppose that
is a normal hypersurface of degree $$\begin{eqnarray}X\subseteq \mathbf{P}^{n+1}\end{eqnarray}$$
$$\begin{eqnarray}X\subseteq \mathbf{P}^{n+1}\end{eqnarray}$$
 $d\geqslant n+2$
with at worst canonical singularities, and let
$d\geqslant n+2$
with at worst canonical singularities, and let
 $\unicode[STIX]{x1D707}:X^{\prime }\longrightarrow X$
be a resolution of singularities. Then the canonical bundle
$\unicode[STIX]{x1D707}:X^{\prime }\longrightarrow X$
be a resolution of singularities. Then the canonical bundle
 $K_{X^{\prime }}$
of
$K_{X^{\prime }}$
of
 $X^{\prime }$
satisfies
$X^{\prime }$
satisfies
 $\operatorname{(BVA)}_{d-n-2}$
.
$\operatorname{(BVA)}_{d-n-2}$
.
Indeed, (i), (ii) and (iii) are clear from the definition, while (iv) is a consequence of (ii) and the elementary fact that
![]() ${\mathcal{O}}_{\mathbf{P}}(p)$
is
${\mathcal{O}}_{\mathbf{P}}(p)$
is
![]() $p$
-very ample. For (v), it follows from the definition of canonical singularities that
$p$
-very ample. For (v), it follows from the definition of canonical singularities that
where
![]() $H$
is the pull-back of the hyperplane bundle on
$H$
is the pull-back of the hyperplane bundle on
![]() $X$
and
$X$
and
![]() $E$
is effective. So the assertion follows from (i) and (iv).
$E$
is effective. So the assertion follows from (i) and (iv).
The relevance of this notion to questions of gonality arises from the following elementary observation.
Lemma 1.3. Let
![]() $C$
be a smooth projective curve of genus
$C$
be a smooth projective curve of genus
![]() $g$
whose canonical bundle
$g$
whose canonical bundle
![]() $K_{C}$
satisfies
$K_{C}$
satisfies
![]() $\operatorname{(BVA)}_{p}$
. Then
$\operatorname{(BVA)}_{p}$
. Then
Proof. We may suppose
![]() $g\geqslant 2$
. Let
$g\geqslant 2$
. Let
![]() $A$
be a globally generated line bundle of degree
$A$
be a globally generated line bundle of degree
![]() $d\leqslant g-1$
on
$d\leqslant g-1$
on
![]() $C$
. Then the divisor
$C$
. Then the divisor
![]() $\unicode[STIX]{x1D709}$
of any section of
$\unicode[STIX]{x1D709}$
of any section of
![]() $A$
fails to impose independent conditions on
$A$
fails to impose independent conditions on
![]() $|K_{C}|$
. Hence if
$|K_{C}|$
. Hence if
![]() $K_{C}$
satisfies
$K_{C}$
satisfies
![]() $\operatorname{(BVA)}_{p}$
, then one must have
$\operatorname{(BVA)}_{p}$
, then one must have
![]() $d\geqslant p+2$
.◻
$d\geqslant p+2$
.◻
We now turn to coverings by curves of specified gonality. Let
![]() $X$
be an irreducible projective variety.
$X$
be an irreducible projective variety.
Definition 1.4. A covering family of curves of gonality
![]() $c$
on
$c$
on
![]() $X$
consists of a smooth family
$X$
consists of a smooth family
of irreducible projective curves parametrized by an irreducible variety
![]() $T$
, together with a dominant morphism
$T$
, together with a dominant morphism
satisfying both the following:
-
(i) for a general point
 $t\in T$
, the fibre
$t\in T$
, the fibre
 $C_{t}=_{\text{def}}\,\unicode[STIX]{x1D70B}^{-1}(t)$
is a smooth curve with
$C_{t}=_{\text{def}}\,\unicode[STIX]{x1D70B}^{-1}(t)$
is a smooth curve with
 $\operatorname{gon}(C_{t})=c$
;
$\operatorname{gon}(C_{t})=c$
; -
(ii) for general
 $t\in T$
, the map
$t\in T$
, the map
 $f_{t}:C_{t}\longrightarrow X$
is birational onto its image.
$f_{t}:C_{t}\longrightarrow X$
is birational onto its image.
By standard arguments, the existence of such a family is equivalent to asking that
![]() $X$
contains a (possibly singular) curve of gonality
$X$
contains a (possibly singular) curve of gonality
![]() $c$
passing through a general point.
$c$
passing through a general point.
Remark 1.5. We make some remarks about the formal properties of this definition.
-
(i) After replacing
 $T$
by a desingularization, one can suppose without loss of generality that
$T$
by a desingularization, one can suppose without loss of generality that
 $T$
and
$T$
and
 ${\mathcal{C}}$
are non-singular.
${\mathcal{C}}$
are non-singular. -
(ii) Given a covering family as above, after restricting to a suitable subvariety of
 $T$
we may suppose without loss of generality that
$T$
we may suppose without loss of generality that
 $\dim {\mathcal{C}}=\dim X$
, so that, in particular, the morphism is generically finite.
$\dim {\mathcal{C}}=\dim X$
, so that, in particular, the morphism is generically finite. $$\begin{eqnarray}f:{\mathcal{C}}\longrightarrow X\end{eqnarray}$$
$$\begin{eqnarray}f:{\mathcal{C}}\longrightarrow X\end{eqnarray}$$
-
(iii) Suppose that
 $\unicode[STIX]{x1D70B}:{\mathcal{C}}\longrightarrow T$
,
$\unicode[STIX]{x1D70B}:{\mathcal{C}}\longrightarrow T$
,
 $f:{\mathcal{C}}\longrightarrow X$
is a covering family with
$f:{\mathcal{C}}\longrightarrow X$
is a covering family with
 ${\mathcal{C}}$
and
${\mathcal{C}}$
and
 $T$
non-singular, and let
$T$
non-singular, and let
 $\unicode[STIX]{x1D708}:{\mathcal{C}}^{\prime }\longrightarrow {\mathcal{C}}$
be the blowing up of
$\unicode[STIX]{x1D708}:{\mathcal{C}}^{\prime }\longrightarrow {\mathcal{C}}$
be the blowing up of
 ${\mathcal{C}}$
along a smooth center. Then there is a non-empty Zariski-open subset
${\mathcal{C}}$
along a smooth center. Then there is a non-empty Zariski-open subset
 $T_{0}\subseteq T$
over which the restrictions of the two maps coincide. (Since blowing up along a divisor has no effect, we can assume that this center has codimension greater than or equal to
$T_{0}\subseteq T$
over which the restrictions of the two maps coincide. (Since blowing up along a divisor has no effect, we can assume that this center has codimension greater than or equal to $$\begin{eqnarray}{\mathcal{C}}^{\prime }\longrightarrow T,\quad {\mathcal{C}}\longrightarrow T\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}^{\prime }\longrightarrow T,\quad {\mathcal{C}}\longrightarrow T\end{eqnarray}$$
 $2$
, and hence maps to a subset of
$2$
, and hence maps to a subset of
 $T$
having codimension greater than or equal to
$T$
having codimension greater than or equal to
 $1$
.)
$1$
.)
-
(iv) Let
 $\unicode[STIX]{x1D70B}:{\mathcal{C}}\longrightarrow T$
,
$\unicode[STIX]{x1D70B}:{\mathcal{C}}\longrightarrow T$
,
 $f:{\mathcal{C}}\longrightarrow X$
be a covering family with
$f:{\mathcal{C}}\longrightarrow X$
be a covering family with
 ${\mathcal{C}}$
and
${\mathcal{C}}$
and
 $T$
smooth, and let be a birational morphism. Then there is a non-empty Zariski-open subset
$T$
smooth, and let be a birational morphism. Then there is a non-empty Zariski-open subset $$\begin{eqnarray}\unicode[STIX]{x1D707}:X^{\prime }\longrightarrow X\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}:X^{\prime }\longrightarrow X\end{eqnarray}$$
 $T_{0}\subseteq T$
so that the restriction
$T_{0}\subseteq T$
so that the restriction
 $\unicode[STIX]{x1D70B}_{0}:{\mathcal{C}}_{0}\longrightarrow T_{0}$
extends to a family (In fact, by a suitable sequence of blow-ups, we can construct a modification
$\unicode[STIX]{x1D70B}_{0}:{\mathcal{C}}_{0}\longrightarrow T_{0}$
extends to a family (In fact, by a suitable sequence of blow-ups, we can construct a modification $$\begin{eqnarray}f^{\prime }:{\mathcal{C}}_{0}\longrightarrow X^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}f^{\prime }:{\mathcal{C}}_{0}\longrightarrow X^{\prime }.\end{eqnarray}$$
 ${\mathcal{C}}^{\prime }\longrightarrow {\mathcal{C}}$
that admits an extension
${\mathcal{C}}^{\prime }\longrightarrow {\mathcal{C}}$
that admits an extension
 $f^{\prime }:{\mathcal{C}}^{\prime }\longrightarrow X^{\prime }$
. The assertion then follows from (iii).)
$f^{\prime }:{\mathcal{C}}^{\prime }\longrightarrow X^{\prime }$
. The assertion then follows from (iii).)
As in the Introduction, we focus on the smallest gonality of such a covering family.
Definition 1.6. The covering gonality
![]() $\operatorname{cov.gon}(X)$
of
$\operatorname{cov.gon}(X)$
of
![]() $X$
is the least integer
$X$
is the least integer
![]() $c>0$
for which such a covering family exists.
$c>0$
for which such a covering family exists.
It follows from Remark 1.5(iv) that this is indeed a birational invariant.
Example 1.7 (Examples of covering gonality).
Here are some examples where the covering gonality can be estimated or computed.
-
(i) Let
 $X$
be a
$X$
be a
 $K3$
surface. By a theorem of Bogomolov and Mumford [Reference Mori and MukaiMM83, p. 351]
$K3$
surface. By a theorem of Bogomolov and Mumford [Reference Mori and MukaiMM83, p. 351]
 $X$
is covered by (singular) elliptic curves. Hence
$X$
is covered by (singular) elliptic curves. Hence
 $\operatorname{cov.gon}(X)=2$
. If
$\operatorname{cov.gon}(X)=2$
. If
 $X$
is an abelian surface, then similarly
$X$
is an abelian surface, then similarly
 $\operatorname{cov.gon}(X)=2$
: in fact,
$\operatorname{cov.gon}(X)=2$
: in fact,
 $X$
is covered by curves of genus less than or equal to
$X$
is covered by curves of genus less than or equal to
 $2$
.Footnote
5
$2$
.Footnote
5
-
(ii) Let
 $X=C_{2}$
be the symmetric square of a smooth curve
$X=C_{2}$
be the symmetric square of a smooth curve
 $C$
of genus
$C$
of genus
 $g\geqslant 3$
. Then
$g\geqslant 3$
. Then
 $X$
is covered by copies of
$X$
is covered by copies of
 $C$
via the double covering
$C$
via the double covering
 $C\times C\longrightarrow X$
. Bastianelli [Reference BastianelliBas12] shows that these curves compute the covering gonality of
$C\times C\longrightarrow X$
. Bastianelli [Reference BastianelliBas12] shows that these curves compute the covering gonality of
 $X$
, i.e.
$X$
, i.e.
 $\operatorname{cov.gon}(X)=\operatorname{gon}(C)$
.
$\operatorname{cov.gon}(X)=\operatorname{gon}(C)$
. -
(iii) Let
 $X\subseteq \mathbf{P}^{3}$
be a smooth surface of degree
$X\subseteq \mathbf{P}^{3}$
be a smooth surface of degree
 $d\geqslant 4$
, let
$d\geqslant 4$
, let
 $x\in X$
be a general point, and let
$x\in X$
be a general point, and let
 $T_{x}\subseteq \mathbf{P}^{3}$
be the tangent plane to
$T_{x}\subseteq \mathbf{P}^{3}$
be the tangent plane to
 $X$
at
$X$
at
 $x$
. Then is an irreducible plane curve of degree
$x$
. Then is an irreducible plane curve of degree $$\begin{eqnarray}D_{x}=T_{x}\cap X\end{eqnarray}$$
$$\begin{eqnarray}D_{x}=T_{x}\cap X\end{eqnarray}$$
 $d$
with a double point, which has gonality
$d$
with a double point, which has gonality
 $d-2$
. Therefore
$d-2$
. Therefore
 $\operatorname{cov.gon}(X)\leqslant d-2$
. In fact, Lopez and Pirola [Reference Lopez and PirolaLP95] show that this is the unique family of minimal gonality for general
$\operatorname{cov.gon}(X)\leqslant d-2$
. In fact, Lopez and Pirola [Reference Lopez and PirolaLP95] show that this is the unique family of minimal gonality for general
 $X$
, and hence
$X$
, and hence
 $\operatorname{cov.gon}(X)=d-2$
. One can evidently arrange for such a curve to pass through two general points of
$\operatorname{cov.gon}(X)=d-2$
. One can evidently arrange for such a curve to pass through two general points of
 $X$
, and hence
$X$
, and hence
 $\operatorname{conn.gon}(X)=d-2$
.
$\operatorname{conn.gon}(X)=d-2$
.
-
(iv) Suppose now that
 $X\subseteq \mathbf{P}^{4}$
is a smooth threefold of degree
$X\subseteq \mathbf{P}^{4}$
is a smooth threefold of degree
 $d\geqslant 5$
. A dimension count predicts that
$d\geqslant 5$
. A dimension count predicts that
 $X$
should be covered by a two-dimensional family of plane curves of degree
$X$
should be covered by a two-dimensional family of plane curves of degree
 $d$
with triple points. One can prove, either directly or (as Jason Starr pointed out) by a degeneration, that this is indeed the case. Hence and the same inequality holds a fortiori for hypersurfaces of degree
$d$
with triple points. One can prove, either directly or (as Jason Starr pointed out) by a degeneration, that this is indeed the case. Hence and the same inequality holds a fortiori for hypersurfaces of degree $$\begin{eqnarray}\operatorname{cov.gon}(X)\leqslant d-3,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{cov.gon}(X)\leqslant d-3,\end{eqnarray}$$
 $d$
and larger dimension. It then follows from Corollary 1.11 that
$d$
and larger dimension. It then follows from Corollary 1.11 that
 $\operatorname{cov.gon}(X)=d-3$
for a general threefold of degree
$\operatorname{cov.gon}(X)=d-3$
for a general threefold of degree
 $d$
.
$d$
.
-
(v) Let
 $X\subseteq \mathbf{P}^{n+1}$
be a hypersurface of degree
$X\subseteq \mathbf{P}^{n+1}$
be a hypersurface of degree
 $d>n$
having an ordinary singular point
$d>n$
having an ordinary singular point
 $p\in X$
of multiplicity
$p\in X$
of multiplicity
 $n$
: in particular,
$n$
: in particular,
 $X$
has only canonical singularities. Projection from
$X$
has only canonical singularities. Projection from
 $p$
gives rise to a rational map
$p$
gives rise to a rational map
 $X{\dashrightarrow}\mathbf{P}^{n}$
of degree
$X{\dashrightarrow}\mathbf{P}^{n}$
of degree
 $d-n$
, and the inverse images of lines
$d-n$
, and the inverse images of lines
 $\ell \subseteq \mathbf{P}^{n}$
then yield a covering of
$\ell \subseteq \mathbf{P}^{n}$
then yield a covering of
 $X$
by curves of gonality less than or equal to
$X$
by curves of gonality less than or equal to
 $d-n$
. Therefore
$d-n$
. Therefore
 $\operatorname{cov.gon}(X)\leqslant d-n$
, and it follows from Corollary 1.11 below that in fact
$\operatorname{cov.gon}(X)\leqslant d-n$
, and it follows from Corollary 1.11 below that in fact
 $\operatorname{cov.gon}(X)=d-n$
.
$\operatorname{cov.gon}(X)=d-n$
.
Remark 1.8 (Covering gonality of very general hypersurface).
By starting with some of the ideas used in the proof of Theorem C in § 3, the first author, Ciliberto, Flamini and Supino [Reference Bastianelli, Ciliberto, Flamini and SupinoBCFS17] have computed the covering gonality of a very general hypersurface
![]() $X_{d}\subseteq \mathbf{P}^{n+1}$
of degree
$X_{d}\subseteq \mathbf{P}^{n+1}$
of degree
![]() $d\gg 0$
in almost all cases. Specifically, they show that
$d\gg 0$
in almost all cases. Specifically, they show that
The numerics here are essentially what one finds by looking for plane curves with singular points covering
![]() $X$
, as in Examples 1.7(iii) and (iv).
$X$
, as in Examples 1.7(iii) and (iv).
Recall that if
![]() $D\longrightarrow C$
is a branched covering of irreducible projective curves, then
$D\longrightarrow C$
is a branched covering of irreducible projective curves, then
![]() $\operatorname{gon}(D)\geqslant \operatorname{gon}(C)$
. This implies the analogous statement for covering gonality.
$\operatorname{gon}(D)\geqslant \operatorname{gon}(C)$
. This implies the analogous statement for covering gonality.
Lemma 1.9. Let
![]() $f:X\longrightarrow Y$
be a generically finite surjective mapping between irreducible projective varieties. Then
$f:X\longrightarrow Y$
be a generically finite surjective mapping between irreducible projective varieties. Then
The main theorem of this section asserts that the covering gonality of a smooth projective variety is bounded by the positivity of its canonical bundle. When
![]() $\dim X=2$
the statement was established in [Reference Knutsen, Syzdek and SzembergKSS09, § 3].
$\dim X=2$
the statement was established in [Reference Knutsen, Syzdek and SzembergKSS09, § 3].
Theorem 1.10. Let
![]() $X$
be a smooth projective variety, and suppose that there is an integer
$X$
be a smooth projective variety, and suppose that there is an integer
![]() $p\geqslant 0$
such that its canonical bundle
$p\geqslant 0$
such that its canonical bundle
![]() $K_{X}$
satisfies property
$K_{X}$
satisfies property
![]() $\operatorname{(BVA)}_{p}$
. Then
$\operatorname{(BVA)}_{p}$
. Then
Proof. This is very elementary. Suppose that
is a covering family of curves of gonality
![]() $c$
. Thanks to Remark 1.5(i) and (ii), there is no loss of generality in assuming that
$c$
. Thanks to Remark 1.5(i) and (ii), there is no loss of generality in assuming that
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() $T$
are smooth, and that
$T$
are smooth, and that
![]() $f$
is generically finite. Then
$f$
is generically finite. Then
where
![]() $E=\text{Ram}(f)$
is the ramification divisor of
$E=\text{Ram}(f)$
is the ramification divisor of
![]() $f$
. On the other hand, since
$f$
. On the other hand, since
![]() $\unicode[STIX]{x1D70B}$
is smooth one has
$\unicode[STIX]{x1D70B}$
is smooth one has
for every
![]() $t\in T$
. Furthermore, if
$t\in T$
. Furthermore, if
![]() $t\in T$
is general, then
$t\in T$
is general, then
![]() $C_{t}$
meets the effective divisor
$C_{t}$
meets the effective divisor
![]() $E$
properly, and its image
$E$
properly, and its image
will not be contained in the exceptional set
![]() $Z(K_{X})\subseteq X$
arising in Definition 1.1. Since by definition
$Z(K_{X})\subseteq X$
arising in Definition 1.1. Since by definition
![]() $f_{t}:C_{t}\longrightarrow X$
is birational onto its image, it follows from (*), (**) and Example 1.2(iii) that
$f_{t}:C_{t}\longrightarrow X$
is birational onto its image, it follows from (*), (**) and Example 1.2(iii) that
![]() $K_{C_{t}}$
satisfies property
$K_{C_{t}}$
satisfies property
![]() $\operatorname{(BVA)}_{p}$
. Hence
$\operatorname{(BVA)}_{p}$
. Hence
![]() $c\geqslant p+2$
thanks to Lemma 1.3.◻
$c\geqslant p+2$
thanks to Lemma 1.3.◻
The assertion of Theorem A is then covered by the following.
Corollary 1.11. Let
![]() $X\subseteq \mathbf{P}^{n+1}$
be a smooth hypersurface of degree
$X\subseteq \mathbf{P}^{n+1}$
be a smooth hypersurface of degree
![]() $d\geqslant n+2$
. Then
$d\geqslant n+2$
. Then
The same statement holds if
![]() $X$
is normal with only canonical singularities.
$X$
is normal with only canonical singularities.
Note that if we allow canonical singularities, then Example 1.7(v) shows that the statement is best possible for all
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
![]() $d\geqslant n+2$
. When
$d\geqslant n+2$
. When
![]() $n=1$
we recover Noether’s result that a smooth plane curve of degree
$n=1$
we recover Noether’s result that a smooth plane curve of degree
![]() $d$
has gonality
$d$
has gonality
![]() $d-1$
.
$d-1$
.
Proof of Corollary 1.11.
When
![]() $X$
is smooth, its canonical bundle
$X$
is smooth, its canonical bundle
![]() $\unicode[STIX]{x1D714}_{X}={\mathcal{O}}_{X}(d-n-2)$
is already
$\unicode[STIX]{x1D714}_{X}={\mathcal{O}}_{X}(d-n-2)$
is already
![]() $(d-n-2)$
-very ample. For the second statement, we can pass to a desingularization, and then Example 1.2(v) applies.◻
$(d-n-2)$
-very ample. For the second statement, we can pass to a desingularization, and then Example 1.2(v) applies.◻
We observe next that a sufficiently positive divisor on any smooth variety has large covering gonality.
Corollary 1.12. Let
![]() $M$
be a smooth projective variety, and let
$M$
be a smooth projective variety, and let
![]() $A$
be a very ample line bundle on
$A$
be a very ample line bundle on
![]() $M$
. Fix an integer
$M$
. Fix an integer
![]() $e$
such that
$e$
such that
![]() $|(e+2)A+K_{M}|$
is basepoint-free, and let
$|(e+2)A+K_{M}|$
is basepoint-free, and let
be any smooth divisor. Then
Proof. In fact,
where
![]() $|E|$
is free. Since
$|E|$
is free. Since
![]() $A$
is very ample,
$A$
is very ample,
![]() ${\mathcal{O}}_{X}((d-e-2)A)$
is
${\mathcal{O}}_{X}((d-e-2)A)$
is
![]() $(d-e-2)$
-very ample, and therefore
$(d-e-2)$
-very ample, and therefore
![]() $K_{X}$
satisfies Property
$K_{X}$
satisfies Property
![]() $\operatorname{(BVA)}_{d-e-2}$
.◻
$\operatorname{(BVA)}_{d-e-2}$
.◻
Finally, we say a word about the connecting gonality of an irreducible projective variety
![]() $X$
. An evident modification of Definition 1.7 leads to the notion of a family of curves of gonality
$X$
. An evident modification of Definition 1.7 leads to the notion of a family of curves of gonality
![]() $c$
connecting two general points of
$c$
connecting two general points of
![]() $X$
, and as in the Introduction the least such gonality is defined to be
$X$
, and as in the Introduction the least such gonality is defined to be
![]() $\operatorname{conn.gon}(X)$
. Clearly
$\operatorname{conn.gon}(X)$
. Clearly
and the example of a uniruled variety which is not rationally connected shows that the inequality can be strict. Moreover the analogue of Lemma 1.9 remains valid. Unfortunately, we do not at the moment know any useful ways of controlling this invariant. For example, when
![]() $X$
is the symmetric square of a curve of large genus, as in Example 1.7(ii), we suspect that
$X$
is the symmetric square of a curve of large genus, as in Example 1.7(ii), we suspect that
![]() $\operatorname{cov.gon}(X)<\operatorname{conn.gon}(X)$
, but we do not know how to prove this.
$\operatorname{cov.gon}(X)<\operatorname{conn.gon}(X)$
, but we do not know how to prove this.
2 Voisin’s invariant
In this section, we sketch the basic properties of a Chow-theoretic measure of irrationality. This material was suggested to us by Claire Voisin.
Let
![]() $X$
be a smooth complex projective variety of dimension
$X$
be a smooth complex projective variety of dimension
![]() $n$
. A one parameter family of Chow-constant
$n$
. A one parameter family of Chow-constant
![]() $zero$
-cycles on
$zero$
-cycles on
![]() $X$
consists of a family of effective zero-cycles
$X$
consists of a family of effective zero-cycles
![]() $\{Z_{t}\}_{t\in T}$
parametrized by a smooth irreducible curve
$\{Z_{t}\}_{t\in T}$
parametrized by a smooth irreducible curve
![]() $T$
with the property that all the
$T$
with the property that all the
![]() $Z_{t}$
are rationally equivalent to a fixed cycle. Voisin’s idea is to consider the least degree of such cycles passing through a general point of
$Z_{t}$
are rationally equivalent to a fixed cycle. Voisin’s idea is to consider the least degree of such cycles passing through a general point of
![]() $X$
.
$X$
.
Definition 2.1. We define the Voisin invariant
![]() $v(X)$
to be the least positive integer
$v(X)$
to be the least positive integer
![]() $v>0$
with the following property.
$v>0$
with the following property.
For any proper algebraic subset
![]() $W\subseteq X$
, and a general point
$W\subseteq X$
, and a general point
![]() $x\in X$
not lying on
$x\in X$
not lying on
![]() $W$
, there exists a non-constant one-parameter family
$W$
, there exists a non-constant one-parameter family
![]() $\{Z_{t}\}_{t\in T}$
of reduced Chow-constant zero-cycles of degree
$\{Z_{t}\}_{t\in T}$
of reduced Chow-constant zero-cycles of degree
![]() $v$
with the properties that:
$v$
with the properties that:
-
(i)
 $x\in Z_{0}$
for some
$x\in Z_{0}$
for some
 $0\in T$
;
$0\in T$
; -
(ii)
 $\text{Supp}(Z_{t})$
is disjoint from
$\text{Supp}(Z_{t})$
is disjoint from
 $W$
for general
$W$
for general
 $t\in T$
.
$t\in T$
.
It follows from (ii) that
![]() $v(X)$
is a birational invariant of
$v(X)$
is a birational invariant of
![]() $X$
.
$X$
.
Example 2.2. One evidently has
If
![]() $\operatorname{CH}_{0}(X)$
is trivial, then
$\operatorname{CH}_{0}(X)$
is trivial, then
![]() $v(X)=1$
. In particular, if
$v(X)=1$
. In particular, if
![]() $X$
is Chow-trivial but not uniruled, then
$X$
is Chow-trivial but not uniruled, then
![]() $v(X)<\operatorname{cov.gon}(X)$
.
$v(X)<\operatorname{cov.gon}(X)$
.
The following result generalizes Theorem 1.10.
Theorem 2.3. If
![]() $K_{X}$
satisfies
$K_{X}$
satisfies
![]() $\operatorname{(BVA)}_{p}$
, then
$\operatorname{(BVA)}_{p}$
, then
![]() $v(X)\geqslant p+2$
.
$v(X)\geqslant p+2$
.
Proof. Assume there is a one-dimensional family of Chow-constant zero-cycles of degree
![]() $v$
passing through a general point of
$v$
passing through a general point of
![]() $X$
. Then by a standard argument they must fit together in an
$X$
. Then by a standard argument they must fit together in an
![]() $n$
-dimensional family of cycles dominating
$n$
-dimensional family of cycles dominating
![]() $X$
. More precisely, there exists an
$X$
. More precisely, there exists an
![]() $n$
-dimensional smooth irreducible variety
$n$
-dimensional smooth irreducible variety
![]() $S$
admitting a morphism
$S$
admitting a morphism
with the following properties:
-
(i) the pull-back
to $$\begin{eqnarray}Z_{S}=_{\text{def}}S\times _{\operatorname{Sym}^{v}(X)}(X\times \operatorname{Sym}^{v-1}(X))\end{eqnarray}$$
$$\begin{eqnarray}Z_{S}=_{\text{def}}S\times _{\operatorname{Sym}^{v}(X)}(X\times \operatorname{Sym}^{v-1}(X))\end{eqnarray}$$
 $S$
of the universal zero-cycle dominates
$S$
of the universal zero-cycle dominates
 $X$
;
$X$
;
-
(ii)
 $Z_{S}$
is generically étale over
$Z_{S}$
is generically étale over
 $S$
(i.e. the generic cycle
$S$
(i.e. the generic cycle
 $Z_{s}$
is reduced).
$Z_{s}$
is reduced).
After possibly shrinking
![]() $S$
, we are free to suppose that
$S$
, we are free to suppose that
![]() $Z_{S}$
is actually étale over
$Z_{S}$
is actually étale over
![]() $S$
. In this setting, Mumford [Reference MumfordMum69] constructs a trace mapping
$S$
. In this setting, Mumford [Reference MumfordMum69] constructs a trace mapping
for
![]() $\unicode[STIX]{x1D702}\in H^{0}(X,K_{X})$
and
$\unicode[STIX]{x1D702}\in H^{0}(X,K_{X})$
and
![]() $s\in S$
,
$s\in S$
,
![]() $\text{Tr}_{F}(\unicode[STIX]{x1D702})$
is determined by the formula
$\text{Tr}_{F}(\unicode[STIX]{x1D702})$
is determined by the formula
Lemma 2.4 below shows that because
![]() $S$
is constructed from Chow-constant one-parameter families, one has
$S$
is constructed from Chow-constant one-parameter families, one has
But this implies that the points of the general cycle
![]() $Z_{s}$
satisfy the Cayley–Bacharach property with respect to
$Z_{s}$
satisfy the Cayley–Bacharach property with respect to
![]() $|K_{X}|$
, i.e. any
$|K_{X}|$
, i.e. any
![]() $n$
-form vanishing at all but one of the points of
$n$
-form vanishing at all but one of the points of
![]() $Z_{s}$
vanish at the remaining one. (Compare for instance [Reference Bastianelli, Cortini and De PoiBCDP14, Proposition 2.3] or [Reference Guerra and PirolaGP08, §§ 3.2–3.4].) Therefore
$Z_{s}$
vanish at the remaining one. (Compare for instance [Reference Bastianelli, Cortini and De PoiBCDP14, Proposition 2.3] or [Reference Guerra and PirolaGP08, §§ 3.2–3.4].) Therefore
![]() $\operatorname{(BVA)}_{v-1}$
fails for
$\operatorname{(BVA)}_{v-1}$
fails for
![]() $X$
, as required.◻
$X$
, as required.◻
Lemma 2.4. In the setting of the proof of Theorem 2.3,
Sketch of proof.
For lack of a suitable reference, we sketch the modifications of the arguments from [Reference MumfordMum69] required to verify the assertion. Note to begin with that to give a one-parameter family
![]() $\{Z_{t}\}_{t\in T}$
of Chow-constant degree
$\{Z_{t}\}_{t\in T}$
of Chow-constant degree
![]() $v$
zero-cycles amounts to specifying maps
$v$
zero-cycles amounts to specifying maps
together with a morphism
satisfying
where
![]() $t_{0}\in T$
is a fixed point. In the setting of the proof of Theorem 2.3, we can therefore suppose (after possibly shrinking and replacing
$t_{0}\in T$
is a fixed point. In the setting of the proof of Theorem 2.3, we can therefore suppose (after possibly shrinking and replacing
![]() $S$
by an étale covering) that we have:
$S$
by an étale covering) that we have:
-
(i) a smooth surjective morphism
 $\unicode[STIX]{x1D70B}:S\longrightarrow B$
of relative dimension one together with a section
$\unicode[STIX]{x1D70B}:S\longrightarrow B$
of relative dimension one together with a section
 $\unicode[STIX]{x1D70E}:B\longrightarrow S$
fixing a base-point on the fibres of
$\unicode[STIX]{x1D70E}:B\longrightarrow S$
fixing a base-point on the fibres of
 $\unicode[STIX]{x1D70B}$
;
$\unicode[STIX]{x1D70B}$
; -
(ii) a morphism
 $A:S\longrightarrow \operatorname{Sym}^{w}(X)$
;
$A:S\longrightarrow \operatorname{Sym}^{w}(X)$
; -
(iii) a morphism
satisfying $$\begin{eqnarray}H:S\times \mathbf{P}^{1}\longrightarrow \operatorname{Sym}^{v+w}(X)\end{eqnarray}$$
(*)
$$\begin{eqnarray}H:S\times \mathbf{P}^{1}\longrightarrow \operatorname{Sym}^{v+w}(X)\end{eqnarray}$$
(*) $$\begin{eqnarray}H(s,0)=F(\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D70B}(s))+A(s),\quad H(s,\infty )=F(s)+A(s).\end{eqnarray}$$
$$\begin{eqnarray}H(s,0)=F(\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D70B}(s))+A(s),\quad H(s,\infty )=F(s)+A(s).\end{eqnarray}$$
Now consider a form
![]() $\unicode[STIX]{x1D702}\in H^{0}(X,K_{X})$
. By the functoriality of Mumford’s construction, one has
$\unicode[STIX]{x1D702}\in H^{0}(X,K_{X})$
. By the functoriality of Mumford’s construction, one has
On the other hand, thanks to (*), we deduce that
the last equality arising from the fact that
![]() $F\circ \unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D70B}$
factors through a variety of dimension
$F\circ \unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D70B}$
factors through a variety of dimension
![]() $n-1$
. But since
$n-1$
. But since
![]() $\mathbf{P}^{1}$
carries no canonical forms,
$\mathbf{P}^{1}$
carries no canonical forms,
is independent of
![]() $\unicode[STIX]{x1D706}\in \mathbf{P}^{1}$
. Thus
$\unicode[STIX]{x1D706}\in \mathbf{P}^{1}$
. Thus
![]() $\operatorname{Tr}_{F}(\unicode[STIX]{x1D702})=0$
, as required.◻
$\operatorname{Tr}_{F}(\unicode[STIX]{x1D702})=0$
, as required.◻
3 Degree of irrationality of projective hypersurfaces
In this section we discuss the degree of irrationality and give the proof of Theorem C from the Introduction.
We start with some general remarks about the irrationality degree
![]() $\operatorname{irr}(X)$
of an irreducible complex projective variety
$\operatorname{irr}(X)$
of an irreducible complex projective variety
![]() $X$
of dimension
$X$
of dimension
![]() $n$
. Recall from the Introduction that this is defined to be the least degree of a dominant rational map
$n$
. Recall from the Introduction that this is defined to be the least degree of a dominant rational map
Equivalently, one can characterize
![]() $\operatorname{irr}(X)$
as the minimal degree of a field extension
$\operatorname{irr}(X)$
as the minimal degree of a field extension
where the
![]() $t_{i}\in \mathbf{C}(X)$
are algebraically independent rational functions on
$t_{i}\in \mathbf{C}(X)$
are algebraically independent rational functions on
![]() $X$
. We refer to [Reference YoshiharaYos94, Reference Tokunaga and YoshiharaTY95, Reference YoshiharaYos98, Reference YoshiharaYos96, Reference BastianelliBas12] for some computations and estimations of
$X$
. We refer to [Reference YoshiharaYos94, Reference Tokunaga and YoshiharaTY95, Reference YoshiharaYos98, Reference YoshiharaYos96, Reference BastianelliBas12] for some computations and estimations of
![]() $\operatorname{irr}(X)$
, especially in the case of surfaces.
$\operatorname{irr}(X)$
, especially in the case of surfaces.
Given a rational covering
![]() $f:X{\dashrightarrow}\mathbf{P}^{n}$
, observe that the inverse images of lines
$f:X{\dashrightarrow}\mathbf{P}^{n}$
, observe that the inverse images of lines
![]() $\ell \subseteq \mathbf{P}^{n}$
determine a family of curves of gonality less than or equal to
$\ell \subseteq \mathbf{P}^{n}$
determine a family of curves of gonality less than or equal to
![]() $\deg (f)$
connecting two general points on
$\deg (f)$
connecting two general points on
![]() $X$
. This shows that
$X$
. This shows that
The existence of rationally connected varieties that are not rational, as well as many other examples, illustrates that the gonality invariants can be strictly smaller than
![]() $\operatorname{irr}(X)$
. However, by combining (3.1) with Theorem 1.10 we find the following.
$\operatorname{irr}(X)$
. However, by combining (3.1) with Theorem 1.10 we find the following.
Corollary 3.1. Let
![]() $X$
be a smooth projective variety whose canonical bundle
$X$
be a smooth projective variety whose canonical bundle
![]() $K_{X}$
satisfies Property
$K_{X}$
satisfies Property
![]() $\operatorname{(BVA)}_{p}$
for some
$\operatorname{(BVA)}_{p}$
for some
![]() $p\geqslant 0$
. Then
$p\geqslant 0$
. Then
As above (Examples 1.2(v) and 1.7(v)), equality holds for the desingularization of a hypersurface of degree
![]() $d$
in
$d$
in
![]() $\mathbf{P}^{n+1}$
with an ordinary
$\mathbf{P}^{n+1}$
with an ordinary
![]() $n$
-fold point.
$n$
-fold point.
Remark 3.2. One can give a direct proof of (a strengthening of) the corollary using results and methods of [Reference Lopez and PirolaLP95, Reference BastianelliBas12, Reference Bastianelli, Cortini and De PoiBCDP14, Reference Guerra and PirolaGP08], involving correspondences with null trace and the Cayley–Bacharach property, along the lines of the proof of Theorem 2.3. Specifically, consider a dominant rational map
between two smooth projective
![]() $n$
-folds. We claim that
$n$
-folds. We claim that
In fact, given any rational covering
![]() $f$
one has a trace map
$f$
one has a trace map
on canonical forms. As before, for
![]() $\unicode[STIX]{x1D702}\in H^{0}(X,K_{X})$
and a general point
$\unicode[STIX]{x1D702}\in H^{0}(X,K_{X})$
and a general point
![]() $y\in Y$
, one can view the value of
$y\in Y$
, one can view the value of
![]() $\text{Tr}_{f}(\unicode[STIX]{x1D702})$
at
$\text{Tr}_{f}(\unicode[STIX]{x1D702})$
at
![]() $y$
as being computed by averaging the values of
$y$
as being computed by averaging the values of
![]() $\unicode[STIX]{x1D702}$
over the fibre
$\unicode[STIX]{x1D702}$
over the fibre
![]() $f^{-1}(y)$
of
$f^{-1}(y)$
of
![]() $y$
. It follows (as in the proof of Theorem 2.3) that if
$y$
. It follows (as in the proof of Theorem 2.3) that if
![]() $H^{0}(Y,K_{Y})=0$
, then
$H^{0}(Y,K_{Y})=0$
, then
![]() $f^{-1}(y)$
satisfies the Cayley–Bacharach property with respect to
$f^{-1}(y)$
satisfies the Cayley–Bacharach property with respect to
![]() $|K_{X}|$
, i.e. any
$|K_{X}|$
, i.e. any
![]() $n$
-form vanishing on all but one of the points of
$n$
-form vanishing on all but one of the points of
![]() $f^{-1}(y)$
must vanish on the remaining one. (See for instance [Reference Bastianelli, Cortini and De PoiBCDP14, Proposition 2.3] or [Reference Guerra and PirolaGP08, §§ 3.2–3.4].) In particular, these points do not impose independent conditions on
$f^{-1}(y)$
must vanish on the remaining one. (See for instance [Reference Bastianelli, Cortini and De PoiBCDP14, Proposition 2.3] or [Reference Guerra and PirolaGP08, §§ 3.2–3.4].) In particular, these points do not impose independent conditions on
![]() $H^{0}(X,K_{X})$
, and (3.2) follows.
$H^{0}(X,K_{X})$
, and (3.2) follows.
Remark 3.3. Voisin has pointed out to us that one can also prove a variant of the statement (3.2) from the previous remark. Specifically, consider a smooth polarized projective
![]() $n$
-fold
$n$
-fold
![]() $(X,H)$
with the property that the resulting primitive Hodge-structure
$(X,H)$
with the property that the resulting primitive Hodge-structure
![]() $H^{n}(X,\mathbf{Q})_{\text{prim}}$
is irreducible: this holds for instance for a very general hypersurface
$H^{n}(X,\mathbf{Q})_{\text{prim}}$
is irreducible: this holds for instance for a very general hypersurface
![]() $X\subseteq \mathbf{P}^{n+1}$
of degree greater than
$X\subseteq \mathbf{P}^{n+1}$
of degree greater than
![]() $n+2$
. Suppose moreover that
$n+2$
. Suppose moreover that
![]() $K_{X}$
satisfies property
$K_{X}$
satisfies property
![]() $\operatorname{(BVA)}_{p}$
with
$\operatorname{(BVA)}_{p}$
with
![]() $p\geqslant 1$
. If
$p\geqslant 1$
. If
![]() $Y$
is any smooth projective variety of dimension
$Y$
is any smooth projective variety of dimension
![]() $n$
, then any rational covering
$n$
, then any rational covering
must actually be birational. In fact, assume to the contrary that
![]() $f$
is not birational. The mapping
$f$
is not birational. The mapping
![]() $f^{\ast }H^{0}(Y,K_{Y})\longrightarrow H^{0}(X,K_{X})$
, which in any event is injective, must be surjective or zero, else it would give a non-trivial Hodge substructure of
$f^{\ast }H^{0}(Y,K_{Y})\longrightarrow H^{0}(X,K_{X})$
, which in any event is injective, must be surjective or zero, else it would give a non-trivial Hodge substructure of
![]() $H^{n}(X,\mathbf{Q})_{\text{prim}}$
. The former possibility is impossible since
$H^{n}(X,\mathbf{Q})_{\text{prim}}$
. The former possibility is impossible since
![]() $K_{X}$
satisfies
$K_{X}$
satisfies
![]() $\operatorname{(BVA)}_{1}$
, and therefore it must be the case that
$\operatorname{(BVA)}_{1}$
, and therefore it must be the case that
![]() $H^{0}(Y,K_{Y})=0$
. Then the previous remark applies. (Compare [Reference Guerra and PirolaGP08, Proposition 3.5.2].)
$H^{0}(Y,K_{Y})=0$
. Then the previous remark applies. (Compare [Reference Guerra and PirolaGP08, Proposition 3.5.2].)
We now turn to the case of a smooth hypersurface
of dimension
![]() $n\geqslant 2$
and degree
$n\geqslant 2$
and degree
![]() $d\geqslant n+2$
. Projection from a point of
$d\geqslant n+2$
. Projection from a point of
![]() $X$
shows that in any event
$X$
shows that in any event
and by [Reference Bastianelli, Cortini and De PoiBCDP14, Theorem 1.2] (or Corollary 1.11 above) one has the lower bound
Example 3.4. Interestingly enough, it can actually happen that
![]() $\operatorname{irr}(X)<d-1$
. For instance, suppose that
$\operatorname{irr}(X)<d-1$
. For instance, suppose that
![]() $X\subseteq \mathbf{P}^{3}$
is a surface containing two disjoint lines
$X\subseteq \mathbf{P}^{3}$
is a surface containing two disjoint lines
![]() $\ell _{1},\ell _{2}\subseteq X$
. Then the line joining general points
$\ell _{1},\ell _{2}\subseteq X$
. Then the line joining general points
![]() $p_{1}\in \ell _{1},p_{2}\in \ell _{2}$
meets
$p_{1}\in \ell _{1},p_{2}\in \ell _{2}$
meets
![]() $X$
at
$X$
at
![]() $(d-2)$
residual points, and this defines a rational mapping
$(d-2)$
residual points, and this defines a rational mapping
of degree
![]() $d-2$
. There are a few other examples of a similar flavor, and it is established in [Reference Bastianelli, Cortini and De PoiBCDP14, Theorem 1.3] that these are the only surfaces of degree
$d-2$
. There are a few other examples of a similar flavor, and it is established in [Reference Bastianelli, Cortini and De PoiBCDP14, Theorem 1.3] that these are the only surfaces of degree
![]() $d\geqslant 5$
in
$d\geqslant 5$
in
![]() $\mathbf{P}^{3}$
for which
$\mathbf{P}^{3}$
for which
![]() $\operatorname{irr}(X)=d-2$
. In a similar way, if
$\operatorname{irr}(X)=d-2$
. In a similar way, if
![]() $X\subseteq \mathbf{P}^{2k+1}$
contains two disjoint
$X\subseteq \mathbf{P}^{2k+1}$
contains two disjoint
![]() $k$
-planes, then
$k$
-planes, then
![]() $\operatorname{irr}(X)\leqslant d-2$
, but apparently no examples are known of hypersurfaces of odd dimension greater than or equal to
$\operatorname{irr}(X)\leqslant d-2$
, but apparently no examples are known of hypersurfaces of odd dimension greater than or equal to
![]() $5$
for which equality fails in (3.3). (See [Reference Bastianelli, Cortini and De PoiBCDP14, 4.13, 4.14].)
$5$
for which equality fails in (3.3). (See [Reference Bastianelli, Cortini and De PoiBCDP14, 4.13, 4.14].)
Our main goal is to establish Theorem C from the Introduction. We will work with the following.
Set-Up 3.5. Denote by
![]() $X\subseteq \mathbf{P}^{n+1}$
a smooth hypersurface of degree
$X\subseteq \mathbf{P}^{n+1}$
a smooth hypersurface of degree
![]() $d$
, and suppose we are given a rational covering
$d$
, and suppose we are given a rational covering
of degree
![]() $\unicode[STIX]{x1D6FF}$
. We assume that we are in one of the following two situations:
$\unicode[STIX]{x1D6FF}$
. We assume that we are in one of the following two situations:
-
(a)
 $d\geqslant 2n+1$
and
$d\geqslant 2n+1$
and
 $\unicode[STIX]{x1D6FF}\leqslant d-2$
; or
$\unicode[STIX]{x1D6FF}\leqslant d-2$
; or -
(b)
 $d\geqslant 2n+2$
and
$d\geqslant 2n+2$
and
 $\unicode[STIX]{x1D6FF}\leqslant d-1$
.
$\unicode[STIX]{x1D6FF}\leqslant d-1$
.
The argument will draw on some constructions and results of [Reference Bastianelli, Cortini and De PoiBCDP14]. Specifically, the rational mapping
![]() $f:X{\dashrightarrow}\mathbf{P}^{n}$
is given by a correspondence
$f:X{\dashrightarrow}\mathbf{P}^{n}$
is given by a correspondence
and for any
![]() $y\in \mathbf{P}^{n}$
we can view the fibre
$y\in \mathbf{P}^{n}$
we can view the fibre
![]() $Z_{y}$
, which in general consists of
$Z_{y}$
, which in general consists of
![]() $\unicode[STIX]{x1D6FF}$
distinct points of
$\unicode[STIX]{x1D6FF}$
distinct points of
![]() $X$
, as a subset of
$X$
, as a subset of
![]() $\mathbf{P}^{n+1}$
. With this notation one has the following.
$\mathbf{P}^{n+1}$
. With this notation one has the following.
Proposition 3.6. Assume that we are in the situation of Set-Up 3.5(a) or (b).
-
(i) For general
 $y\in \mathbf{P}^{n}$
the fibre
$y\in \mathbf{P}^{n}$
the fibre
 $Z_{y}\subseteq \mathbf{P}^{n+1}$
lies on a line
$Z_{y}\subseteq \mathbf{P}^{n+1}$
lies on a line  $$\begin{eqnarray}\ell _{y}\subseteq \mathbf{P}^{n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\ell _{y}\subseteq \mathbf{P}^{n+1}.\end{eqnarray}$$
-
(ii) A general point of
 $\mathbf{P}^{n+1}$
lies on exactly one of these lines.
$\mathbf{P}^{n+1}$
lies on exactly one of these lines.
These facts are established in [Reference Bastianelli, Cortini and De PoiBCDP14, Theorem 2.5, Lemma 4.1] using the ideas involving correspondences with null trace recalled in Remark 3.2 above.
We now explain the basic geometric idea of the proof of Theorem C. Assume that
![]() $f$
is not projection from a point. For general
$f$
is not projection from a point. For general
![]() $y\in \mathbf{P}^{n}$
, write
$y\in \mathbf{P}^{n}$
, write
where
![]() $F_{y}$
is a zero-cycle of degree
$F_{y}$
is a zero-cycle of degree
![]() $d-\unicode[STIX]{x1D6FF}$
, and recall that we already know that
$d-\unicode[STIX]{x1D6FF}$
, and recall that we already know that
![]() $d-\unicode[STIX]{x1D6FF}\leqslant n$
. As
$d-\unicode[STIX]{x1D6FF}\leqslant n$
. As
![]() $y$
varies over a suitable rational subvariety of
$y$
varies over a suitable rational subvariety of
![]() $\mathbf{P}^{n}$
, the
$\mathbf{P}^{n}$
, the
![]() $F_{y}$
(or subcycles thereof) will sweep out a subvariety
$F_{y}$
(or subcycles thereof) will sweep out a subvariety
![]() $S\subseteq X$
of dimension
$S\subseteq X$
of dimension
![]() $s\geqslant 1$
having covering gonality
$s\geqslant 1$
having covering gonality
![]() $e\leqslant d-\unicode[STIX]{x1D6FF}$
. We prove that
$e\leqslant d-\unicode[STIX]{x1D6FF}$
. We prove that
![]() $e$
and
$e$
and
![]() $s$
are related by the inequality
$s$
are related by the inequality
meaning roughly that if
![]() $s$
is small, then
$s$
is small, then
![]() $e$
cannot be too large. On the other hand, a variant of the arguments of [Reference EinEin88, Reference VoisinVoi96] shows that if
$e$
cannot be too large. On the other hand, a variant of the arguments of [Reference EinEin88, Reference VoisinVoi96] shows that if
![]() $e<d-2n+s$
, then a very general hypersurface of degree
$e<d-2n+s$
, then a very general hypersurface of degree
![]() $d$
does not contain an irreducible subvariety
$d$
does not contain an irreducible subvariety
![]() $S\subseteq X$
of dimension
$S\subseteq X$
of dimension
![]() $s>0$
with
$s>0$
with
![]() $\operatorname{cov.gon}(S)=e$
(Proposition 3.8). This turns out to contradict (*) when
$\operatorname{cov.gon}(S)=e$
(Proposition 3.8). This turns out to contradict (*) when
![]() $d\geqslant 2n+2$
, and with a little more care a similar argument works when
$d\geqslant 2n+2$
, and with a little more care a similar argument works when
![]() $d=2n+1$
.
$d=2n+1$
.
Moving to details, we start by fixing some further notation. We assume until the end of the proof of Theorem C that we are in the situation of Set-Up 3.5(a) or (b), so that Proposition 3.6 holds. In classical language, the lines
![]() $\{\ell _{y}\}$
form a congruence of lines, i.e. a family of lines parametrized by an irreducible
$\{\ell _{y}\}$
form a congruence of lines, i.e. a family of lines parametrized by an irreducible
![]() $n$
-dimensional subvariety
$n$
-dimensional subvariety
of the Grassmannian of lines in
![]() $\mathbf{P}^{n+1}$
. Statement (ii) of the Proposition asserts that the congruence has order one: if
$\mathbf{P}^{n+1}$
. Statement (ii) of the Proposition asserts that the congruence has order one: if
![]() $W_{0}\subseteq B_{0}\times \mathbf{P}^{n+1}$
is the restriction to
$W_{0}\subseteq B_{0}\times \mathbf{P}^{n+1}$
is the restriction to
![]() $B_{0}$
of the tautological point-line correspondence in
$B_{0}$
of the tautological point-line correspondence in
![]() $\mathbf{G}\times \mathbf{P}^{n+1}$
, this means that the projection
$\mathbf{G}\times \mathbf{P}^{n+1}$
, this means that the projection
is birational, and it implies that
![]() $B_{0}$
is rational.Footnote
6
$B_{0}$
is rational.Footnote
6
Replacing
![]() $B_{0}$
by a desingularization
$B_{0}$
by a desingularization
![]() $B\longrightarrow B_{0}$
, we arrive at the following basic diagram.
$B\longrightarrow B_{0}$
, we arrive at the following basic diagram.

Here
![]() $B$
is a smooth rational
$B$
is a smooth rational
![]() $n$
-fold mapping birationally to its image in the Grassmannian
$n$
-fold mapping birationally to its image in the Grassmannian
![]() $\mathbf{G}$
, and
$\mathbf{G}$
, and
![]() $\unicode[STIX]{x1D70B}:W\longrightarrow B$
is the pull-back to
$\unicode[STIX]{x1D70B}:W\longrightarrow B$
is the pull-back to
![]() $B$
of the tautological
$B$
of the tautological
![]() $\mathbf{P}^{1}$
-bundle on
$\mathbf{P}^{1}$
-bundle on
![]() $\mathbf{G}$
. The mapping
$\mathbf{G}$
. The mapping
![]() $\unicode[STIX]{x1D707}:W\longrightarrow \mathbf{P}^{n+1}$
is birational, and we define
$\unicode[STIX]{x1D707}:W\longrightarrow \mathbf{P}^{n+1}$
is birational, and we define
![]() $X^{\prime }\subseteq W$
to be the proper transform of
$X^{\prime }\subseteq W$
to be the proper transform of
![]() $X$
in
$X$
in
![]() $W$
. Thus
$W$
. Thus
![]() $X^{\prime }$
is a reduced and irreducible divisor in
$X^{\prime }$
is a reduced and irreducible divisor in
![]() $W$
of relative degree
$W$
of relative degree
![]() $\unicode[STIX]{x1D6FF}$
over
$\unicode[STIX]{x1D6FF}$
over
![]() $B$
, and
$B$
, and
![]() $X^{\prime }\longrightarrow B$
is a generically finite morphism of degree
$X^{\prime }\longrightarrow B$
is a generically finite morphism of degree
![]() $\unicode[STIX]{x1D6FF}$
that represents birationally the original mapping
$\unicode[STIX]{x1D6FF}$
that represents birationally the original mapping
![]() $f:X{\dashrightarrow}\mathbf{P}^{n}$
.
$f:X{\dashrightarrow}\mathbf{P}^{n}$
.
Keeping this notation, we now give the following proof.
Proof of Theorem C.
Let
be the full pre-image of
![]() $X$
in
$X$
in
![]() $W$
, so that
$W$
, so that
![]() $X^{\ast }$
is a (possibly non-reduced) divisor in
$X^{\ast }$
is a (possibly non-reduced) divisor in
![]() $W$
of relative degree
$W$
of relative degree
![]() $d$
over
$d$
over
![]() $B$
. We can write
$B$
. We can write
![]() $X^{\ast }=X^{\prime }+F$
, where
$X^{\ast }=X^{\prime }+F$
, where
![]() $F$
is a divisor of relative degree
$F$
is a divisor of relative degree
![]() $d-\unicode[STIX]{x1D6FF}\geqslant 1$
over
$d-\unicode[STIX]{x1D6FF}\geqslant 1$
over
![]() $B$
. Now fix any irreducible component
$B$
. Now fix any irreducible component
![]() $Y\subseteq F$
that dominates
$Y\subseteq F$
that dominates
![]() $B$
, and view
$B$
, and view
![]() $Y$
as a reduced irreducible variety of dimension
$Y$
as a reduced irreducible variety of dimension
![]() $n$
. Thus
$n$
. Thus
![]() $Y$
sits in a diagram
$Y$
sits in a diagram

and we have
Put
and let
![]() $s=\dim S$
. Suppose first that
$s=\dim S$
. Suppose first that
![]() $s=0$
, i.e. that
$s=0$
, i.e. that
![]() $S$
consists of a single point
$S$
consists of a single point
![]() $p\in X$
. This means that all the lines in the congruence pass through
$p\in X$
. This means that all the lines in the congruence pass through
![]() $p$
, and hence
$p$
, and hence
![]() $f$
must be projection from
$f$
must be projection from
![]() $p$
. Therefore we may henceforth assume that
$p$
. Therefore we may henceforth assume that
![]() $s\geqslant 1$
.
$s\geqslant 1$
.
Note next that
![]() $\operatorname{cov.gon}(S)\leqslant e$
. In fact, one can choose a rational subvariety
$\operatorname{cov.gon}(S)\leqslant e$
. In fact, one can choose a rational subvariety
![]() $L\subseteq B$
of dimension
$L\subseteq B$
of dimension
![]() $s$
with the property that an irreducible component
$s$
with the property that an irreducible component
![]() $Y^{\ast }\subseteq Y$
of the inverse image of
$Y^{\ast }\subseteq Y$
of the inverse image of
![]() $L$
in
$L$
in
![]() $Y$
is generically finite over
$Y$
is generically finite over
![]() $S$
. Since
$S$
. Since
![]() $\deg (Y^{\ast }\longrightarrow L)\leqslant e$
, and since
$\deg (Y^{\ast }\longrightarrow L)\leqslant e$
, and since
![]() $L$
is rational, we see that
$L$
is rational, we see that
![]() $\operatorname{cov.gon}(Y^{\ast })\leqslant e$
. Hence Lemma 1.9 applies to show that
$\operatorname{cov.gon}(Y^{\ast })\leqslant e$
. Hence Lemma 1.9 applies to show that
![]() $\operatorname{cov.gon}(S)\leqslant e$
.
$\operatorname{cov.gon}(S)\leqslant e$
.
Now denote by
![]() $K_{W/\mathbf{P}}=K_{W/\mathbf{P}^{n+1}}$
the relative canonical bundle of
$K_{W/\mathbf{P}}=K_{W/\mathbf{P}^{n+1}}$
the relative canonical bundle of
![]() $\unicode[STIX]{x1D707}$
, i.e. the ramification divisor of
$\unicode[STIX]{x1D707}$
, i.e. the ramification divisor of
![]() $\unicode[STIX]{x1D707}$
, and consider a general fibre
$\unicode[STIX]{x1D707}$
, and consider a general fibre
![]() $\ell =\ell _{y}$
of
$\ell =\ell _{y}$
of
![]() $\unicode[STIX]{x1D70B}$
, i.e. a general line in our congruence. Recall that by a classical and elementary calculation, one has
$\unicode[STIX]{x1D70B}$
, i.e. a general line in our congruence. Recall that by a classical and elementary calculation, one has
[Reference ArrondoArr02, Lemma 1.1]. On the other hand, since
![]() $\dim \unicode[STIX]{x1D707}(Y)=s$
we claim that
$\dim \unicode[STIX]{x1D707}(Y)=s$
we claim that
This follows from a standard computation, but we sketch a proof in Appendix A (Corollary A.6). Therefore the contribution from
![]() $Y$
to the intersection product in (3.9) is greater than or equal to
$Y$
to the intersection product in (3.9) is greater than or equal to
![]() $(n-s)e$
, so in other words
$(n-s)e$
, so in other words
Now recall that we assume that
![]() $s=\dim S\geqslant 1$
. Then it follows from Proposition 3.8 below that
$s=\dim S\geqslant 1$
. Then it follows from Proposition 3.8 below that
Combining this with (*), one finds that
But
when
![]() $1\leqslant s\leqslant n-1$
, which forces
$1\leqslant s\leqslant n-1$
, which forces
![]() $d\leqslant 2n+1$
. Therefore, if
$d\leqslant 2n+1$
. Therefore, if
![]() $d\geqslant 2n+2$
and
$d\geqslant 2n+2$
and
![]() $\unicode[STIX]{x1D6FF}\leqslant d-1$
, then
$\unicode[STIX]{x1D6FF}\leqslant d-1$
, then
![]() $s=0$
, i.e.
$s=0$
, i.e.
![]() $f$
is given by projection from a point.
$f$
is given by projection from a point.
Suppose next that
![]() $d=2n+1$
. Here it remains to rule out the possibility that
$d=2n+1$
. Here it remains to rule out the possibility that
![]() $s=n-1$
and
$s=n-1$
and
![]() $e=n=d-n-1$
. In this case,
$e=n=d-n-1$
. In this case,
![]() $Y$
is the unique irreducible component of the exceptional locus that dominates
$Y$
is the unique irreducible component of the exceptional locus that dominates
![]() $B$
, and
$B$
, and
We claim that the mapping
![]() $Y\longrightarrow S$
is birational to a
$Y\longrightarrow S$
is birational to a
![]() $\mathbf{P}^{1}$
bundle over
$\mathbf{P}^{1}$
bundle over
![]() $S$
. In fact, as in [Reference Kollár and SmithKS04, p. 113],
$S$
. In fact, as in [Reference Kollár and SmithKS04, p. 113],
![]() $Y$
is birational to an exceptional divisor in a sequence of blowings-up of
$Y$
is birational to an exceptional divisor in a sequence of blowings-up of
![]() $\operatorname{Bl}_{S}(\mathbf{P}^{n+1})$
along smooth centers dominating
$\operatorname{Bl}_{S}(\mathbf{P}^{n+1})$
along smooth centers dominating
![]() $S$
, and then (3.11) implies that
$S$
, and then (3.11) implies that
![]() $Y$
is birational to the dominating exceptional divisor of the blow-up of
$Y$
is birational to the dominating exceptional divisor of the blow-up of
![]() $S$
itself. Now let
$S$
itself. Now let
![]() $C\approx \mathbf{P}^{1}$
be a generic fibre of
$C\approx \mathbf{P}^{1}$
be a generic fibre of
![]() $Y\longrightarrow S$
, and write
$Y\longrightarrow S$
, and write
![]() $C^{\prime }$
being a curve which is finite over its image
$C^{\prime }$
being a curve which is finite over its image
![]() $\unicode[STIX]{x1D70B}(C)$
. Thus each of the components of
$\unicode[STIX]{x1D70B}(C)$
. Thus each of the components of
![]() $C^{\prime }$
has gonality less than or equal to
$C^{\prime }$
has gonality less than or equal to
![]() $e-1=d-n-2$
. We assert that
$e-1=d-n-2$
. We assert that
Grant this for now. One checks moreover that as one varies the fibres of
![]() $Y\longrightarrow S$
, the resulting curves
$Y\longrightarrow S$
, the resulting curves
![]() $C^{\prime }$
generically cover
$C^{\prime }$
generically cover
![]() $S$
. It follows that
$S$
. It follows that
which contradicts Proposition 3.8 and we are done.
It remains to prove (3.12). Since
![]() $C$
is a fibre of
$C$
is a fibre of
![]() $Y\longrightarrow S$
, any component of
$Y\longrightarrow S$
, any component of
![]() $C^{\prime }$
that contracts would have to map to a different point of
$C^{\prime }$
that contracts would have to map to a different point of
![]() $S$
. This means that all the lines
$S$
. This means that all the lines
![]() $\ell _{z}\subseteq \mathbf{P}^{n+1}$
parametrized by
$\ell _{z}\subseteq \mathbf{P}^{n+1}$
parametrized by
![]() $z\in \unicode[STIX]{x1D70B}(C)\subseteq B$
share two points in common, and hence coincide. This in turn implies that
$z\in \unicode[STIX]{x1D70B}(C)\subseteq B$
share two points in common, and hence coincide. This in turn implies that
![]() $\unicode[STIX]{x1D70B}(C)$
maps to a point in the Grassmannian
$\unicode[STIX]{x1D70B}(C)$
maps to a point in the Grassmannian
![]() $\mathbf{G}$
. But this is impossible since we may assume that
$\mathbf{G}$
. But this is impossible since we may assume that
![]() $\unicode[STIX]{x1D70B}(C)$
passes through a general point of
$\unicode[STIX]{x1D70B}(C)$
passes through a general point of
![]() $B$
.◻
$B$
.◻
Remark 3.7 (Fundamental locus of a congruence of order one).
An argument similar to the one just completed shows that every irreducible component of the fundamental locus of a congruence of order one other than a star of lines has covering gonality less than or equal to
![]() $n$
.
$n$
.
We next show that the computations of [Reference EinEin88, Reference VoisinVoi96] lead to the following statement. This is essentially the same argument that appears in [Reference FakhruddinFak02].
Proposition 3.8. Let
![]() $X\subseteq \mathbf{P}^{n+1}$
be a very general hypersurface of degree
$X\subseteq \mathbf{P}^{n+1}$
be a very general hypersurface of degree
![]() $d\geqslant 2n$
. If
$d\geqslant 2n$
. If
![]() $X$
contains an irreducible subvariety
$X$
contains an irreducible subvariety
![]() $S\subseteq X$
of dimension
$S\subseteq X$
of dimension
![]() $s>0$
and covering gonality
$s>0$
and covering gonality
![]() $\operatorname{cov.gon}(S)=c$
, then
$\operatorname{cov.gon}(S)=c$
, then
Proof of Proposition 3.8.
Let
![]() $V=H^{0}(\mathbf{P}^{n+1},{\mathcal{O}}_{\mathbf{P}}(d))$
be the vector space of all hypersurfaces of degree
$V=H^{0}(\mathbf{P}^{n+1},{\mathcal{O}}_{\mathbf{P}}(d))$
be the vector space of all hypersurfaces of degree
![]() $d$
, which we view as an affine variety. Let
$d$
, which we view as an affine variety. Let
be the universal hypersurface of degree
![]() $d$
. Denote by
$d$
. Denote by
the two projections, and write
![]() $v=\dim V$
.
$v=\dim V$
.
Suppose now that a very general hypersurface of degree
![]() $d$
contains a subvariety of dimension
$d$
contains a subvariety of dimension
![]() $s$
having covering gonality
$s$
having covering gonality
![]() $c$
. Then by a standard argument there exists a commutative diagram
$c$
. Then by a standard argument there exists a commutative diagram

where
![]() $\unicode[STIX]{x1D70B}:{\mathcal{S}}\longrightarrow T$
is a family of varieties of dimension
$\unicode[STIX]{x1D70B}:{\mathcal{S}}\longrightarrow T$
is a family of varieties of dimension
![]() $s$
having covering gonality
$s$
having covering gonality
![]() $c$
,
$c$
,
![]() $\unicode[STIX]{x1D70C}$
is étale, and
$\unicode[STIX]{x1D70C}$
is étale, and
![]() $f_{t}:S_{t}\longrightarrow X_{\unicode[STIX]{x1D70C}(t)}$
is birational onto its image. In this setting, Ein and Voisin prove that if
$f_{t}:S_{t}\longrightarrow X_{\unicode[STIX]{x1D70C}(t)}$
is birational onto its image. In this setting, Ein and Voisin prove that if
![]() $t\in T$
is a general point, then
$t\in T$
is a general point, then
is generically generated by its global sections (cf. [Reference VoisinVoi96, Theorem 1.4]), where
![]() $S_{t}=\unicode[STIX]{x1D70B}^{-1}(t)$
is the fibre of
$S_{t}=\unicode[STIX]{x1D70B}^{-1}(t)$
is the fibre of
![]() $\unicode[STIX]{x1D70B}$
. This implies that
$\unicode[STIX]{x1D70B}$
. This implies that
where
![]() $H_{S_{t}}$
is the pull-back of the hyperplane bundle from
$H_{S_{t}}$
is the pull-back of the hyperplane bundle from
![]() $\mathbf{P}^{n+1}$
. Thus
$\mathbf{P}^{n+1}$
. Thus
![]() $K_{S_{t}}$
satisfies property
$K_{S_{t}}$
satisfies property
![]() $\operatorname{(BVA)}_{d+s-2n-2}$
, and Theorem 1.10 applies to show that
$\operatorname{(BVA)}_{d+s-2n-2}$
, and Theorem 1.10 applies to show that
![]() $c\geqslant d+s-2n$
.◻
$c\geqslant d+s-2n$
.◻
Remark 3.9 (Ran’s theorem).
As a referee of an earlier version of this paper pointed out, the proof of Theorem C is related to a result of Ran [Reference RanRan91]. Ran’s theorem asserts that if
![]() $S\subseteq \mathbf{P}^{n+1}$
is an irreducible projective variety of dimension
$S\subseteq \mathbf{P}^{n+1}$
is an irreducible projective variety of dimension
![]() $s\leqslant n-1$
, and if the union of the
$s\leqslant n-1$
, and if the union of the
![]() $k$
-secant lines to the regular locus of
$k$
-secant lines to the regular locus of
![]() $S$
fill
$S$
fill
![]() $\mathbf{P}^{n+1}$
, then
$\mathbf{P}^{n+1}$
, then
![]() $k\leqslant s+1$
. At least if one knew that it were smooth, the variety
$k\leqslant s+1$
. At least if one knew that it were smooth, the variety
![]() $Y$
in diagram (3.6) would determine such a family with
$Y$
in diagram (3.6) would determine such a family with
![]() $k=e$
, and hence
$k=e$
, and hence
![]() $e\leqslant s+1$
. Therefore, as above, Proposition 3.8 would yield
$e\leqslant s+1$
. Therefore, as above, Proposition 3.8 would yield
which implies
![]() $d\leqslant 2n+1$
. So when
$d\leqslant 2n+1$
. So when
![]() $d\geqslant 2n+2$
we could infer that
$d\geqslant 2n+2$
we could infer that
![]() $s=0$
, and the case
$s=0$
, and the case
![]() $d=2n+1$
would be treated as before. However, the argument given above not only avoids questions of singularities in applying Ran’s theorem, it also leads to a quick new account of that result, as well as a related theorem of Beheshti and Eisenbud [Reference Beheshti and EisenbudBE10]. This is presented in Appendix A.
$d=2n+1$
would be treated as before. However, the argument given above not only avoids questions of singularities in applying Ran’s theorem, it also leads to a quick new account of that result, as well as a related theorem of Beheshti and Eisenbud [Reference Beheshti and EisenbudBE10]. This is presented in Appendix A.
4 Open problems
In this section, we propose some problems concerning this circle of ideas.
A first natural line of investigation is to compute or estimate the various measures of irrationality for other classes of varieties. As a start, suppose that
is a smooth complete intersection of hypersurfaces of degrees
![]() $2\leqslant d_{1}\leqslant d_{2}\leqslant \cdots \leqslant d_{e}$
. Then
$2\leqslant d_{1}\leqslant d_{2}\leqslant \cdots \leqslant d_{e}$
. Then
and so it follows immediately from Theorem 1.10 that
But it seems almost certain that one can do much better.
Problem 4.1. Find bounds on the birational positivity of
![]() $K_{X}$
(in the sense of Definition 1.1) and the irrationality invariants of
$K_{X}$
(in the sense of Definition 1.1) and the irrationality invariants of
![]() $X$
that are multiplicative in the degrees of the defining equations.
$X$
that are multiplicative in the degrees of the defining equations.
For example, when
![]() $X\subseteq \mathbf{P}^{e+1}$
is a complete intersection curve, it was established in [Reference LazarsfeldLaz97, Exercise 4.12] that
$X\subseteq \mathbf{P}^{e+1}$
is a complete intersection curve, it was established in [Reference LazarsfeldLaz97, Exercise 4.12] that
but this already used some non-trivial vector bundle technology. In higher dimensions one might therefore want to consider first the case that
![]() $X$
is a very general complete intersection of the stated multidegrees. In the codimension two case, for instance, Stapleton [Reference StapletonSta17] shows that if
$X$
is a very general complete intersection of the stated multidegrees. In the codimension two case, for instance, Stapleton [Reference StapletonSta17] shows that if
![]() $X\subseteq \mathbf{P}^{n+2}$
is a very general complete intersection of type
$X\subseteq \mathbf{P}^{n+2}$
is a very general complete intersection of type
![]() $(2,d)$
such that
$(2,d)$
such that
![]() $d\geqslant 2n$
, then
$d\geqslant 2n$
, then
It also seems natural to consider polarized
![]() $K3$
and abelian surfaces of growing degree.
$K3$
and abelian surfaces of growing degree.
Conjecture 4.2. Let
![]() $(S_{d},B_{d})$
be a very general polarized
$(S_{d},B_{d})$
be a very general polarized
![]() $K3$
surface of genus
$K3$
surface of genus
![]() $d$
.Footnote
7
Then
$d$
.Footnote
7
Then
with an analogous statement for a very general abelian surface
![]() $A_{d}$
that carries a polarization of type
$A_{d}$
that carries a polarization of type
![]() $(1,d)$
.
$(1,d)$
.
One might have imagined that the irrationality degree grows linearly in
![]() $d$
, but Stapleton [Reference StapletonSta17] observes that in fact
$d$
, but Stapleton [Reference StapletonSta17] observes that in fact
so at best the growth is sublinear. Recalling that
![]() $\operatorname{cov.gon}(S_{d})=\operatorname{cov.gon}(A_{d})=2$
for every
$\operatorname{cov.gon}(S_{d})=\operatorname{cov.gon}(A_{d})=2$
for every
![]() $d$
(Example 1.7), the conjecture would yield a natural family of examples showing that the covering gonality and the degree of irrationality capture very different phenomena.
$d$
(Example 1.7), the conjecture would yield a natural family of examples showing that the covering gonality and the degree of irrationality capture very different phenomena.
For higher dimensional abelian varieties, the covering gonality already seems very interesting.
Problem 4.3. Let
![]() $A^{g}$
be a very general principally polarized abelian variety of dimension
$A^{g}$
be a very general principally polarized abelian variety of dimension
![]() $g$
. Is it the case that
$g$
. Is it the case that
It follows from a theorem of Pirola [Reference PirolaPir89] that in any event
![]() $\operatorname{cov.gon}(A)\geqslant 3$
when
$\operatorname{cov.gon}(A)\geqslant 3$
when
![]() $\dim A\geqslant 3$
.
$\dim A\geqslant 3$
.
It finally seems very appealing to try to say something about these invariants for important moduli spaces that arise in algebraic geometry. For example, Donagi suggests the following.
Problem 4.4. Find bounds on the irrationality invariants of the moduli space
![]() ${\mathcal{M}}_{g}$
parametrizing curves of genus
${\mathcal{M}}_{g}$
parametrizing curves of genus
![]() $g$
, or the moduli space
$g$
, or the moduli space
![]() ${\mathcal{A}}_{g}$
of principally polarized abelian varieties of dimension
${\mathcal{A}}_{g}$
of principally polarized abelian varieties of dimension
![]() $g$
.Footnote
8
$g$
.Footnote
8
Presumably lower bounds for
![]() ${\mathcal{M}}_{g}$
would be very difficult to establish, and may well be out of reach. On the other hand, upper bounds, which already seem of some interest, are likely to be much more accessible. For instance, an elementary argument with Hurwitz schemes shows that
${\mathcal{M}}_{g}$
would be very difficult to establish, and may well be out of reach. On the other hand, upper bounds, which already seem of some interest, are likely to be much more accessible. For instance, an elementary argument with Hurwitz schemes shows that
where
![]() $h_{g,g+1}$
denotes the Hurwitz number counting degree
$h_{g,g+1}$
denotes the Hurwitz number counting degree
![]() $g+1$
simple coverings of
$g+1$
simple coverings of
![]() $\mathbf{P}^{1}$
with fixed branch points by a curve of genus
$\mathbf{P}^{1}$
with fixed branch points by a curve of genus
![]() $g$
. However, this integer is huge, so a natural problem is to find substantially better upper bounds. Concretely, this amounts to asking for constructions that realize a general curve of genus
$g$
. However, this integer is huge, so a natural problem is to find substantially better upper bounds. Concretely, this amounts to asking for constructions that realize a general curve of genus
![]() $g$
as the fibre of a surface mapping to a curve
$g$
as the fibre of a surface mapping to a curve
![]() $C$
of modest gonality. For
$C$
of modest gonality. For
![]() ${\mathcal{A}}_{g}$
, on the other hand, some lower bounds might be relatively easy to obtain.
${\mathcal{A}}_{g}$
, on the other hand, some lower bounds might be relatively easy to obtain.
In another direction, very little has been established so far about connecting gonality.
Problem 4.5. Develop a stock of examples of varieties
![]() $X$
for which
$X$
for which
![]() $\operatorname{conn.gon}(X)$
can be estimated or computed.
$\operatorname{conn.gon}(X)$
can be estimated or computed.
Many examples suggest that it is quite common for
![]() $\operatorname{cov.gon}(X)\ll \operatorname{irr}(X)$
, but it is not clear at the moment how easy it is for
$\operatorname{cov.gon}(X)\ll \operatorname{irr}(X)$
, but it is not clear at the moment how easy it is for
![]() $\operatorname{cov.gon}(X)$
and
$\operatorname{cov.gon}(X)$
and
![]() $\operatorname{conn.gon}(X)$
to diverge (although it can certainly happen). Similarly, it would be interesting to have a better understanding of Voisin’s invariant
$\operatorname{conn.gon}(X)$
to diverge (although it can certainly happen). Similarly, it would be interesting to have a better understanding of Voisin’s invariant
![]() $v(X)$
.
$v(X)$
.
It might also be interesting to ask about rational coverings of projective space having non-minimal degree.
Problem 4.6. Given an irreducible projective variety
![]() $X$
of dimension
$X$
of dimension
![]() $n$
, what can one say about the possible degrees of rational coverings
$n$
, what can one say about the possible degrees of rational coverings
![]() $X{\dashrightarrow}\mathbf{P}^{n}$
?
$X{\dashrightarrow}\mathbf{P}^{n}$
?
A simple argument suggests that there exists an integer
![]() $\unicode[STIX]{x1D6FF}_{0}$
with the property that given any
$\unicode[STIX]{x1D6FF}_{0}$
with the property that given any
![]() $\unicode[STIX]{x1D6FF}\geqslant \unicode[STIX]{x1D6FF}_{0}$
one can find a covering
$\unicode[STIX]{x1D6FF}\geqslant \unicode[STIX]{x1D6FF}_{0}$
one can find a covering
![]() $X{\dashrightarrow}\mathbf{P}^{n}$
of degree
$X{\dashrightarrow}\mathbf{P}^{n}$
of degree
![]() $\unicode[STIX]{x1D6FF}$
.Footnote
9
Call the least such integer
$\unicode[STIX]{x1D6FF}$
.Footnote
9
Call the least such integer
![]() $\unicode[STIX]{x1D6FF}_{0}(X)$
. How much can
$\unicode[STIX]{x1D6FF}_{0}(X)$
. How much can
![]() $\unicode[STIX]{x1D6FF}_{0}(X)$
deviate from
$\unicode[STIX]{x1D6FF}_{0}(X)$
deviate from
![]() $\operatorname{irr}(X)$
? What are estimates for
$\operatorname{irr}(X)$
? What are estimates for
![]() $\unicode[STIX]{x1D6FF}_{0}(X)$
in the case of very general hypersurfaces
$\unicode[STIX]{x1D6FF}_{0}(X)$
in the case of very general hypersurfaces
![]() $X_{d}\subseteq \mathbf{P}^{n+1}$
? One can also ask what ‘gaps’ can appear in the degrees of rational coverings (or the gonalities of covering families). In the case of surfaces, [Reference Lopez and PirolaLP95, Theorem 1.3, Corollary 1.7] give some statements in this direction.
$X_{d}\subseteq \mathbf{P}^{n+1}$
? One can also ask what ‘gaps’ can appear in the degrees of rational coverings (or the gonalities of covering families). In the case of surfaces, [Reference Lopez and PirolaLP95, Theorem 1.3, Corollary 1.7] give some statements in this direction.
Another natural direction for research is to explore more fully the formal behavior of these invariants. For instance, we have the following problem.
Problem 4.7. What are the variational properties of the various irrationality measures in families?
The example of a general surface
![]() $X\subseteq \mathbf{P}^{3}$
deforming to one containing two lines shows that
$X\subseteq \mathbf{P}^{3}$
deforming to one containing two lines shows that
![]() $\operatorname{irr}(X)$
can decrease under specialization. Are there examples where it increases in a smooth family? This may be more accessible than the corresponding question for rationality itself, which is unknown.
$\operatorname{irr}(X)$
can decrease under specialization. Are there examples where it increases in a smooth family? This may be more accessible than the corresponding question for rationality itself, which is unknown.
It is well established that questions of rationality become particularly interesting and subtle for varieties defined over fields that are not algebraically closed. This suggests the following problem.
Problem 4.8. Study measures of irrationality over non-closed fields.
For instance if
![]() $X$
is defined over a field
$X$
is defined over a field
![]() $k$
, one would want to consider the least degree of a rational covering
$k$
, one would want to consider the least degree of a rational covering
![]() $X{\dashrightarrow}\mathbf{P}^{n}$
defined over
$X{\dashrightarrow}\mathbf{P}^{n}$
defined over
![]() $k$
. Already the case of hypersurfaces seems potentially interesting.
$k$
. Already the case of hypersurfaces seems potentially interesting.
Finally, in a more speculative vein, a number of new techniques have been introduced to study questions of rationality, such as Kollár’s passage to characteristic
![]() $p>0$
[Reference KollárKol95], the Chow-theoretic ideas used by Voisin [Reference VoisinVoi15], and the combination of these by Totaro [Reference TotaroTot16]. There have also been ideas that rationality could be detected in the geometry of derived categories (e.g. [Reference KuznetsovKuz10]). It would be very interesting if further ideas along these lines could be used to say something about measures of irrationality, for example the Voisin invariant
$p>0$
[Reference KollárKol95], the Chow-theoretic ideas used by Voisin [Reference VoisinVoi15], and the combination of these by Totaro [Reference TotaroTot16]. There have also been ideas that rationality could be detected in the geometry of derived categories (e.g. [Reference KuznetsovKuz10]). It would be very interesting if further ideas along these lines could be used to say something about measures of irrationality, for example the Voisin invariant
![]() $v(X)$
mentioned briefly above. Similarly, the papers [Reference LazarsfeldLaz96, Reference Hwang and ToHT12] show that the gonality of a curve
$v(X)$
mentioned briefly above. Similarly, the papers [Reference LazarsfeldLaz96, Reference Hwang and ToHT12] show that the gonality of a curve
![]() $C$
influences various Riemannian and Kähler invariants of varieties associated to
$C$
influences various Riemannian and Kähler invariants of varieties associated to
![]() $C$
, such as the Jacobian variety
$C$
, such as the Jacobian variety
![]() $\text{Jac}(C)$
and certain analytic subvarieties of the surface
$\text{Jac}(C)$
and certain analytic subvarieties of the surface
![]() $C\times C$
. Are there any analogous statements in higher dimensions?
$C\times C$
. Are there any analogous statements in higher dimensions?
Acknowledgements
We are grateful to Ron Donagi, Daniel Litt, Luigi Lombardi, Ernesto Mistretta, John Ottem, Ian Shipman, David Stapleton, Jason Starr and Damiano Testa for helpful discussions. We would also like to acknowledge the influence of Pietro Pirola, who with his colleagues introduced many of the ideas that implicitly play a role here. We are particularly grateful to Claire Voisin, who besides suggesting the numerical improvement we noted above, proposed the material that appears in § 2. We are also grateful to another referee of an earlier version for providing several valuable expository and mathematical suggestions.
Appendix A The theorems of Ran and Beheshti–Eisenbud
The purpose of this appendix is to show how the ideas from the proof of Theorem C give a simple account of both Ran’s theorem [Reference RanRan91] and a related result of Beheshti and Eisenbud [Reference Beheshti and EisenbudBE10].
For smooth varieties, Ran’s result is the following.
Theorem A.1 (Ran [Reference RanRan91]).
Let
![]() $X\subseteq \mathbf{P}^{N}$
be a smooth variety of dimension
$X\subseteq \mathbf{P}^{N}$
be a smooth variety of dimension
![]() $n$
. Let
$n$
. Let
![]() $\operatorname{Sec}^{n+2}X$
be the variety swept out by all of the
$\operatorname{Sec}^{n+2}X$
be the variety swept out by all of the
![]() $(n+2)$
-secant lines of
$(n+2)$
-secant lines of
![]() $X$
. Then
$X$
. Then
Ran works more generally with possibly singular varieties, which requires some preliminary definitions.
Definition A.2. Let
![]() $X\subseteq \mathbf{P}^{N}$
be a variety of dimension
$X\subseteq \mathbf{P}^{N}$
be a variety of dimension
![]() $n$
. Let
$n$
. Let
![]() $X^{0}$
be the smooth locus of
$X^{0}$
be the smooth locus of
![]() $X$
. For
$X$
. For
![]() $k\geqslant 0$
put
$k\geqslant 0$
put
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}_{k}=\{\text{lines }\ell \subseteq \mathbf{P}^{N}\mid \text{length}(\ell \cap X)\geqslant k\text{ and }\text{Supp}(\ell \cap X)\subseteq X^{0}\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{Sec}^{k}X^{0}=\mathop{\bigcup }_{\ell \in \unicode[STIX]{x1D6F4}_{k}}\ell . & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F4}_{k}=\{\text{lines }\ell \subseteq \mathbf{P}^{N}\mid \text{length}(\ell \cap X)\geqslant k\text{ and }\text{Supp}(\ell \cap X)\subseteq X^{0}\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \operatorname{Sec}^{k}X^{0}=\mathop{\bigcup }_{\ell \in \unicode[STIX]{x1D6F4}_{k}}\ell . & \displaystyle \nonumber\end{eqnarray}$$
Ran’s stronger statement is as follows.
Theorem A.3 [Reference RanRan91].
Let
![]() $X\subseteq \mathbf{P}^{N}$
be a (possibly singular) subvariety of dimension
$X\subseteq \mathbf{P}^{N}$
be a (possibly singular) subvariety of dimension
![]() $n$
. Then
$n$
. Then
Proof. Via generic projections, one reduces to the case when
![]() $X\subseteq \mathbf{P}^{N}$
with
$X\subseteq \mathbf{P}^{N}$
with
![]() $N=n+2$
. Assume for a contradiction that
$N=n+2$
. Assume for a contradiction that
![]() $\overline{\operatorname{Sec}^{n+2}X^{0}}=\mathbf{P}^{n+2}$
. In this case, we can find a subvariety
$\overline{\operatorname{Sec}^{n+2}X^{0}}=\mathbf{P}^{n+2}$
. In this case, we can find a subvariety
of dimension
![]() $n+1=N-1$
parametrizing
$n+1=N-1$
parametrizing
![]() $(n+2)$
-secant lines for
$(n+2)$
-secant lines for
![]() $X$
that generically meet
$X$
that generically meet
![]() $X$
only at smooth points. As in § 3, one then arrives at a diagram:
$X$
only at smooth points. As in § 3, one then arrives at a diagram:

where
![]() $B$
is a smooth projective variety of dimension
$B$
is a smooth projective variety of dimension
![]() $N-1=n+1$
mapping birationally to
$N-1=n+1$
mapping birationally to
![]() $B_{0}$
,
$B_{0}$
,
![]() $\unicode[STIX]{x1D70B}:W\longrightarrow B$
is the pull-back to
$\unicode[STIX]{x1D70B}:W\longrightarrow B$
is the pull-back to
![]() $B$
of the tautological
$B$
of the tautological
![]() $\mathbf{P}^{1}$
bundle on
$\mathbf{P}^{1}$
bundle on
![]() $\mathbf{G}$
, and
$\mathbf{G}$
, and
![]() $\unicode[STIX]{x1D707}$
is surjective and generically finite. Denoting by
$\unicode[STIX]{x1D707}$
is surjective and generically finite. Denoting by
![]() ${\mathcal{I}}_{X}\subseteq {\mathcal{O}}_{\mathbf{P}^{N}}$
the ideal sheaf of
${\mathcal{I}}_{X}\subseteq {\mathcal{O}}_{\mathbf{P}^{N}}$
the ideal sheaf of
![]() $X$
, write
$X$
, write
where
![]() $X^{\prime }\subseteq W$
is a closed subscheme of codimension at least 2, and
$X^{\prime }\subseteq W$
is a closed subscheme of codimension at least 2, and
![]() $D$
is an effective divisor on
$D$
is an effective divisor on
![]() $W$
. We may decompose
$W$
. We may decompose
![]() $D$
as a sum
$D$
as a sum
![]() $D=E+E^{\prime },$
where
$D=E+E^{\prime },$
where
![]() $E$
and
$E$
and
![]() $E^{\prime }$
are effective divisors such that every component of
$E^{\prime }$
are effective divisors such that every component of
![]() $E$
dominates
$E$
dominates
![]() $B$
and
$B$
and
![]() $\operatorname{codim}(\unicode[STIX]{x1D70B}(E^{\prime }))\geqslant 1$
. Now set
$\operatorname{codim}(\unicode[STIX]{x1D70B}(E^{\prime }))\geqslant 1$
. Now set
where the
![]() $E_{i}$
are the distinct irreducible components of
$E_{i}$
are the distinct irreducible components of
![]() $E$
. Let
$E$
. Let
![]() $\ell$
be a generic fibre of
$\ell$
be a generic fibre of
![]() $\unicode[STIX]{x1D70B}$
. Our assumption implies that
$\unicode[STIX]{x1D70B}$
. Our assumption implies that
Let
![]() $K_{W/\mathbf{P}^{N}}=K_{W/\mathbf{P}}$
be the ramification divisor of
$K_{W/\mathbf{P}^{N}}=K_{W/\mathbf{P}}$
be the ramification divisor of
![]() $\unicode[STIX]{x1D707}$
. By the adjunction formula,
$\unicode[STIX]{x1D707}$
. By the adjunction formula,
[Reference ArrondoArr02, Lemma 1.1]. Note that
![]() $\unicode[STIX]{x1D707}(E_{i})\cap X^{0}\neq \emptyset$
for each
$\unicode[STIX]{x1D707}(E_{i})\cap X^{0}\neq \emptyset$
for each
![]() $i$
. In fact, each
$i$
. In fact, each
![]() $E_{i}$
meets a general fibre
$E_{i}$
meets a general fibre
![]() $\ell$
of
$\ell$
of
![]() $\unicode[STIX]{x1D70B}$
, while by assumption
$\unicode[STIX]{x1D70B}$
, while by assumption
![]() $\ell$
meets
$\ell$
meets
![]() $X$
only at smooth points. It then follows from Lemma A.5 below that
$X$
only at smooth points. It then follows from Lemma A.5 below that
This implies that
which contradicts the assumption. ◻
In [Reference Beheshti and EisenbudBE10], Beheshti and Eisenbud give an improvement of Ran’s theorem. A similar argument also yields a simplified proof of their result.
Theorem A.4 [Reference Beheshti and EisenbudBE10, Theorem 1.5].
Let
![]() $X\,\subseteq \,\mathbf{P}^{N}$
be a smooth irreducible variety of dimension
$X\,\subseteq \,\mathbf{P}^{N}$
be a smooth irreducible variety of dimension
![]() $n$
. If
$n$
. If
![]() $k\geqslant 2,$
then
$k\geqslant 2,$
then
More generally, for possibly singular
![]() $X$
the same inequality holds for
$X$
the same inequality holds for
![]() $\operatorname{Sec}^{k}X^{0}$
.
$\operatorname{Sec}^{k}X^{0}$
.
Sketch of proof.
As observed by Gruson and Peskine [Reference Gruson and PeskineGP13, p. 554], it is equivalent to show that
for any positive integer
![]() $s$
such that
$s$
such that
![]() $1\leqslant s\leqslant n+1,$
and
$1\leqslant s\leqslant n+1,$
and
![]() $k>(n/s)+1$
. The argument then closely parallels the previous proof. In brief, by a generic projection we can suppose for a contradiction that
$k>(n/s)+1$
. The argument then closely parallels the previous proof. In brief, by a generic projection we can suppose for a contradiction that
![]() $N=n+s+1$
, and that
$N=n+s+1$
, and that
![]() $\overline{\operatorname{Sec}^{k}X^{0}}=\mathbf{P}^{N}$
. We then arrive at an analogue of diagram (A.1) with
$\overline{\operatorname{Sec}^{k}X^{0}}=\mathbf{P}^{N}$
. We then arrive at an analogue of diagram (A.1) with
![]() $\dim B=n+s=N-1.$
Defining
$\dim B=n+s=N-1.$
Defining
![]() $\ell$
and
$\ell$
and
![]() $E=\sum a_{i}E_{i}$
as in the proof of Theorem A.3, one has
$E=\sum a_{i}E_{i}$
as in the proof of Theorem A.3, one has
On the other hand,
thanks to Lemma A.5. But then
But this implies that
![]() $k\leqslant (n/s)+1$
, which contradicts the supposition.◻
$k\leqslant (n/s)+1$
, which contradicts the supposition.◻
Finally, we spell out for the convenience of the reader the inequalities we have drawn on concerning the relative canonical divisor of a generically finite and surjective morphism between smooth varieties.
Lemma A.5. Consider a generically finite surjective morphism
between smooth projective varieties of dimension
![]() $m$
. Let
$m$
. Let
![]() $X\subseteq P$
be an irreducible subvariety of codimension
$X\subseteq P$
be an irreducible subvariety of codimension
![]() $c$
and regular locus
$c$
and regular locus
![]() $X^{0}=X_{\text{reg}}$
, and let
$X^{0}=X_{\text{reg}}$
, and let
![]() $F\subseteq W$
be a prime divisor on
$F\subseteq W$
be a prime divisor on
![]() $W$
. Assume that
$W$
. Assume that
and denote by
![]() $a=\operatorname{ord}_{F}({\mathcal{I}}_{X}\cdot {\mathcal{O}}_{W})$
the order of vanishing along
$a=\operatorname{ord}_{F}({\mathcal{I}}_{X}\cdot {\mathcal{O}}_{W})$
the order of vanishing along
![]() $F$
of the pull-back to
$F$
of the pull-back to
![]() $W$
of the ideal sheaf of
$W$
of the ideal sheaf of
![]() $X$
. Then
$X$
. Then
In particular, taking
![]() $X=\unicode[STIX]{x1D707}(F)$
, this yields the following.
$X=\unicode[STIX]{x1D707}(F)$
, this yields the following.
Corollary A.6. Given
![]() $\unicode[STIX]{x1D707}:W\longrightarrow P$
as above, let
$\unicode[STIX]{x1D707}:W\longrightarrow P$
as above, let
![]() $F\subseteq W$
be a prime divisor on
$F\subseteq W$
be a prime divisor on
![]() $W$
. Suppose that
$W$
. Suppose that
![]() $\dim \unicode[STIX]{x1D707}(F)=s$
. Then
$\dim \unicode[STIX]{x1D707}(F)=s$
. Then
Proof of Lemma A.5.
We argue as in [Reference LazarsfeldLaz04, Lemma 9.2.19]. Choose a general point
![]() $y\in F$
and let
$y\in F$
and let
![]() $x=\unicode[STIX]{x1D707}(y)\in X$
, which we suppose to be a smooth point of
$x=\unicode[STIX]{x1D707}(y)\in X$
, which we suppose to be a smooth point of
![]() $X$
. We can then choose local analytic coordinates
$X$
. We can then choose local analytic coordinates
![]() $z_{1},\ldots ,z_{m}$
on
$z_{1},\ldots ,z_{m}$
on
![]() $W$
centered at
$W$
centered at
![]() $y$
and
$y$
and
![]() $u_{1},\ldots ,u_{m}$
on
$u_{1},\ldots ,u_{m}$
on
![]() $P$
centered at
$P$
centered at
![]() $x$
such that locally
$x$
such that locally
There exist functions
![]() $b_{i}\in \mathbf{C}\{z\}$
such that
$b_{i}\in \mathbf{C}\{z\}$
such that
where
![]() $a_{i}\geqslant 0$
for each
$a_{i}\geqslant 0$
for each
![]() $i$
and
$i$
and
![]() $a_{1},\ldots ,a_{c}\geqslant a$
. Then
$a_{1},\ldots ,a_{c}\geqslant a$
. Then
![]() $\unicode[STIX]{x1D707}^{\ast }(du_{i})=a_{i}z_{1}^{a_{i}-1}b_{i}\,dz_{1}+z_{1}^{a_{i}}\,db_{i}$
, and hence
$\unicode[STIX]{x1D707}^{\ast }(du_{i})=a_{i}z_{1}^{a_{i}-1}b_{i}\,dz_{1}+z_{1}^{a_{i}}\,db_{i}$
, and hence
for some
![]() $g\in \mathbf{C}\{z\}$
. The assertion follows.◻
$g\in \mathbf{C}\{z\}$
. The assertion follows.◻