Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-19T16:38:00.274Z Has data issue: false hasContentIssue false
  • English
  • Français

Diophantine properties of nilpotent Lie groups

Part of: Lie algebras and Lie superalgebras Lie groups Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  13 January 2015

Menny Aka ,
Emmanuel Breuillard ,
Lior Rosenzweig  and
Nicolas de Saxcé
Menny Aka
Affiliation:
Section de mathématiques, EPFL, Station 8 - Bât. MA, CH-1015 Lausanne, Switzerland email menashe-hai.akkaginosar@epfl.ch
Emmanuel Breuillard
Affiliation:
Laboratoire de Mathématiques, Bâtiment 425, Université Paris Sud 11, 91405 Orsay, France email emmanuel.breuillard@math.u-psud.fr
Lior Rosenzweig
Affiliation:
Department of Mathematics, KTH, SE-100 44 Stockholm, Sweden email lior.rosenzweig@gmail.com
Nicolas de Saxcé
Affiliation:
Einstein Institute of Mathematics, Givat Ram, The Hebrew University, Jerusalem, 91904, Israel email saxce@ma.huji.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A finitely generated subgroup 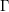${\rm\Gamma}$ of a real Lie group 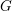$G$ is said to be Diophantine if there is 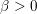${\it\beta}>0$ such that non-trivial elements in the word ball 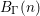$B_{{\rm\Gamma}}(n)$ centered at 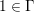$1\in {\rm\Gamma}$ never approach the identity of 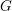$G$ closer than 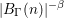$|B_{{\rm\Gamma}}(n)|^{-{\it\beta}}$. A Lie group 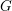$G$ is said to be Diophantine if for every 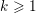$k\geqslant 1$ a random 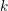$k$-tuple in 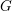$G$ generates a Diophantine subgroup. Semi-simple Lie groups are conjectured to be Diophantine but very little is proven in this direction. We give a characterization of Diophantine nilpotent Lie groups in terms of the ideal of laws of their Lie algebra. In particular we show that nilpotent Lie groups of class at most 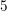$5$, or derived length at most 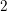$2$, as well as rational nilpotent Lie groups are Diophantine. We also find that there are non-Diophantine nilpotent and solvable (non-nilpotent) Lie groups.

Keywords

word mapsnilpotent Lie groupsDiophantine subgroupequidistribution

MSC classification

Primary: 22E25: Nilpotent and solvable Lie groups 11K60: Diophantine approximation
Secondary: 17B01: Identities, free Lie (super)algebras
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 6 , June 2015 , pp. 1157 - 1188
Copyright
© The Authors 2015 

References

Bass, H., The degree of polynomial growth of finitely generated nilpotent groups, Proc. Lond. Math. Soc. (3) 25 (1972), 603–614.CrossRefGoogle Scholar
Bombieri, E. and Gubler, W., Heights in Diophantine geometry, New Mathematical Monographs, vol. 4 (Cambridge University Press, Cambridge, 2006).Google Scholar
Bourgain, J. and Gamburd, A., On the spectral gap for finitely generated subgroups of SU(2), Invent. Math. 171 (2008), 83–121.CrossRefGoogle Scholar
Breuillard, E., Equidistribution of dense subgroups on nilpotent Lie groups, Ergodic Theory Dynam. Systems 30 (2010), 131–150.CrossRefGoogle Scholar
Breuillard, E., Heights on SL2 and free subgroups, in Geometry, rigidity, and group actions, Chicago Lectures in Mathematics (University Chicago Press, Chicago, IL, 2011), 455–493.Google Scholar
Breuillard, E., Geometry of locally compact groups of polynomial growth and shape of large balls, Groups Geom. Dyn. 8 (2014), 669–732.CrossRefGoogle Scholar
Corwin, L. J. and Greenleaf, F. P., Representations of nilpotent Lie groups and their applications. Part I, inBasic theory and examples, Cambridge Studies in Advanced Mathematics, vol. 18 (Cambridge University Press, Cambridge, 1990).Google Scholar
Dodson, M. M., Hausdorff dimension, lower order and Khintchine’s theorem in metric Diophantine approximation, J. Reine Angew. Math. 432 (1992), 69–76.Google Scholar
Fulton, W. and Harris, J., Representation theory, A first course, readings in mathematics, Graduate Texts in Mathematics, vol. 129 (Springer, New York, NY, 1991).Google Scholar
Gamburd, A., Hoory, S., Shahshahani, M., Shalev, A. and Virág, B., On the girth of random Cayley graphs, Random Structures Algorithms 35 (2009), 100–117.CrossRefGoogle Scholar
Gamburd, A., Jakobson, D. and Sarnak, P., Spectra of elements in the group ring of SU(2), J. Eur. Math. Soc. (JEMS) 1 (1999), 51–85.CrossRefGoogle Scholar
Ganzburg, M. I., Polynomial inequalities on measurable sets and their applications. II. Weighted measures, J. Approx. Theory 106 (2000), 77–109.CrossRefGoogle Scholar
Ganzburg, M. and Brudnyi, J., On an extremal problem for polynomials in n variables, Math. USSR Izv. 7 (1973), 345–356.Google Scholar
Gromov, M., Groups of polynomial growth and expanding maps, Publ. Math. Inst. Hautes Études Sci. 53 (1981), 53–73.CrossRefGoogle Scholar
Guivarc’h, Y., Croissance polynomiale et périodes des fonctions harmoniques, Bull. Soc. Math. France 101 (1973), 353–379.Google Scholar
Hall, M. Jr, The theory of groups (Chelsea Publishing, New York, NY, 1976).Google Scholar
Jarník, V., Über die simultanen diophantischen approximationen, Math. Z. 33 (1931), 505–543.CrossRefGoogle Scholar
Johnson, M., Standard tableaux and Klyachko’s theorem on Lie representations, J. Combin. Theory Ser. A 114 (2007), 151–158.CrossRefGoogle Scholar
Kaloshin, V. and Rodnianski, I., Diophantine properties of elements of SO(3), Geom. Funct. Anal. 11 (2001), 953–970.CrossRefGoogle Scholar
Kleinbock, D. Y. and Margulis, G. A., Flows on homogeneous spaces and Diophantine approximation on manifolds, Ann. of Math. (2) 148 (1998), 339–360.CrossRefGoogle Scholar
Kleinbock, D. and Tomanov, G., Flows on S-arithmetic homogeneous spaces and applications to metric Diophantine approximation, Comment. Math. Helv. 82 (2007), 519–581.CrossRefGoogle Scholar
Kljačko, A. A., Lie elements in a tensor algebra, Sibirsk. Mat. Zh. 15 (1974), 1296–1304, 1430.Google Scholar
Kovács, L. G. and Stöhr, R., A combinatorial proof of Klyachko’s theorem on Lie representations, J. Algebraic Combin. 23 (2006), 225–230.CrossRefGoogle Scholar
Kraskiewicz, W. and Weyman, J., Algebra of coinvariants and the action of coxeter elements, Bayreuth. Math. Schr. 63 (2001), 265–284.Google Scholar
Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory: Presentations of groups in terms of generators and relations, revised edition (Dover, New York, NY, 1976).Google Scholar
Pansu, P., Croissance des boules et des géodésiques fermées dans les nilvariétés, Ergodic Theory Dynam. Systems 3 (1983), 415–445.CrossRefGoogle Scholar
Raghunathan, M. S., Discrete subgroups of Lie groups (Springer, 1972).CrossRefGoogle Scholar
Remez, E., Sur une propriétée extrémale des polynômes de Tchebychef, Comm. Inst. Sci. Kharkov 13 (1936), 93–95.Google Scholar
Reutenauer, C., Free Lie algebras (Oxford University Press, 1993).CrossRefGoogle Scholar
Sarnak, P., Some applications of modular forms, Cambridge Tracts in Mathematics, vol. 99 (Cambridge University Press, 1990).CrossRefGoogle Scholar
Serre, J.-P., Lie algebras and Lie groups, Lecture Notes in Mathematics, vol. 1500, second edition (corrected fifth printing) (Springer, Berlin, 2006).Google Scholar
Thom, A., Convergent sequences in discrete groups, Canad. Math. Bull. 56 (2013), 424–433.CrossRefGoogle Scholar
Thrall, R. M., On symmetrized Kronecker powers and the structure of the free Lie ring, Amer. J. Math. 64 (1942), 371–388.CrossRefGoogle Scholar
Varjú, P. P., Diophantine property in the group of affine transformation of the line, Preprint (2012), arXiv:1211.3647 [math.GR].Google Scholar
Witt, E., Treue Darstellung Liescher Ringe, J. Reine Angew. Math. 177 (1937), 152–160.CrossRefGoogle Scholar