Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-19T16:38:29.514Z Has data issue: false hasContentIssue false
  • English
  • Français

Affine quadrics and the Picard group of the motivic category

Part of: Forms and linear algebraic groups Cycles and subschemes

Published online by Cambridge University Press:  04 July 2019

Alexander Vishik
Alexander Vishik*
Affiliation:
School of Mathematical Sciences, University of Nottingham, Nottingham NG7 2RD, UK email alexander.vishik@nottingham.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the subgroup of the Picard group of Voevodsky’s category of geometric motives 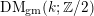$\operatorname{DM}_{\text{gm}}(k;\mathbb{Z}/2)$ generated by the reduced motives of affine quadrics. Our main tools here are the functors of Bachmann [On the invertibility of motives of affine quadrics, Doc. Math. 22 (2017), 363–395], but we also provide an alternative method. We show that the group in question can be described in terms of indecomposable direct summands in the motives of projective quadrics over 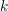$k$. In particular, we describe all the relations among the reduced motives of affine quadrics. We also extend the criterion of motivic equivalence of projective quadrics.

Keywords

quadricPicard groupmotive

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives 11E04: Quadratic forms over general fields 14C25: Algebraic cycles
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 8 , August 2019 , pp. 1500 - 1520
Copyright
© The Author 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bachmann, T., On the invertibility of motives of affine quadrics , Doc. Math. 22 (2017), 363–395.Google Scholar
Bachmann, T., Motivic and real étale stable homotopy theory , Compos. Math. 154 (2018), 883–917.Google Scholar
Bachmann, T. and Vishik, A., Motivic equivalence of affine quadrics , Math. Ann. 371 (2018), 741–751.Google Scholar
Chernousov, V. and Merkurjev, A., Motivic decomposition of projective homogeneous varieties and the Krull-Schmidt theorem , Transform. Groups 11 (2006), 371–386.Google Scholar
Elman, R., Karpenko, N. and Merkurjev, A., The algebraic and geometric theory of quadratic forms , Amer. Math. Soc. Colloq. Publ. 56 (2008), 435 pp.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).Google Scholar
Hu, P., On the Picard group of the stable A1 -homotopy theory , Topology 44 (2005), 609–640.Google Scholar
Karpenko, N., Criteria of motivic equivalence for quadratic forms and central simple algebras , Math. Ann. 317 (2000), 585–611.Google Scholar
Lam, T. Y., Introduction to quadratic forms over fields, Graduate Studies in Mathematics, vol. 67 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Morel, F., On the motivic 𝜋0 of the sphere spectrum , in Axiomatic, enriched and motivic homotopy theory (Kluwer, Dordrecht, 2004), 219–260.Google Scholar
Rost, M., Some new results on the Chow groups of quadrics, Preprint (1990), www.math.uni-bielefeld.de/∼rost/chowqudr.html.Google Scholar
Rost, M., The motive of a Pfister form, Preprint (1998), www.math.uni-bielefeld.de/∼rost/motive.html.Google Scholar
Vishik, A., Integral motives of quadrics, MPIM Preprint 1998-13 (1998), www.mpim-bonn.mpg.de/node/263.Google Scholar
Vishik, A., Motives of quadrics with applications to the theory of quadratic forms , in Geometric methods in the algebraic theory of quadratic forms: Summer School, Lens, 2000, Lecture Notes in Mathematics, vol. 1835, ed. Tignol, J.-P. (Springer, Berlin, 2004), 25–101.Google Scholar
Vishik, A., Excellent connections in the motives of quadrics , Ann. Sci. Éc. Norm. Supér. (4) 44 (2011), 183–195.Google Scholar
Voevodsky, V., Bloch-Kato conjecture for $\mathbb{Z}/2$ -coefficients and algebraic Morava K-theories, Preprint (1995), www.math.uiuc.edu/K-theory/0076.Google Scholar
Voevodsky, V., Triangulated categories of motives over a field , in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000), 188–238.Google Scholar
Voevodsky, V., Motivic cohomology with ℤ/2-coefficients , Publ. Math. Inst. Hautes Études Sci. 98 (2003), 59–104.Google Scholar