Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-25T16:42:11.065Z Has data issue: false hasContentIssue false
  • English
  • Français

An arithmetic count of the lines on a smooth cubic surface

Part of: (Co)homology theory Projective and enumerative geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  08 April 2021

Jesse Leo Kass  and
Kirsten Wickelgren
Jesse Leo Kass
Affiliation:
Department of Mathematics, University of South Carolina, 1523 Greene Street, Columbia, SC29208, USAjkass@umich.edu
Kirsten Wickelgren
Affiliation:
Department of Mathematics, Duke University, 120 Science Dr, Durham, NC27708, USAkirsten.wickelgren@duke.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an arithmetic count of the lines on a smooth cubic surface over an arbitrary field 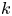$k$, generalizing the counts that over 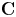${\mathbf {C}}$ there are 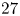$27$ lines, and over 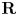${\mathbf {R}}$ the number of hyperbolic lines minus the number of elliptic lines is 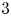$3$. In general, the lines are defined over a field extension 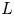$L$ and have an associated arithmetic type 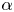$\alpha$ in 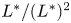$L^*/(L^*)^2$. There is an equality in the Grothendieck–Witt group 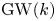$\operatorname {GW}(k)$ of 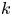$k$,

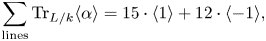\[ \sum_{\text{lines}} \operatorname{Tr}_{L/k} \langle \alpha \rangle = 15 \cdot \langle 1 \rangle + 12 \cdot \langle -1 \rangle, \]
where $\operatorname {Tr}_{L/k}$ denotes the trace 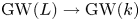$\operatorname {GW}(L) \to \operatorname {GW}(k)$. Taking the rank and signature recovers the results over 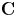${\mathbf {C}}$ and 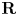${\mathbf {R}}$. To do this, we develop an elementary theory of the Euler number in 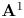$\mathbf {A}^1$-homotopy theory for algebraic vector bundles. We expect that further arithmetic counts generalizing enumerative results in complex and real algebraic geometry can be obtained with similar methods.

Keywords

cubic surfaceEuler classA-homotopy theoryenumerative geometry

MSC classification

Primary: 14N15: Classical problems, Schubert calculus
Secondary: 14F42: Motivic cohomology; motivic homotopy theory 14G27: Other nonalgebraically closed ground fields
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 4 , April 2021 , pp. 677 - 709
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asok, A. and Fasel, J., Comparing Euler classes, Q. J. Math. 67 (2016), 603–635; MR 3609848.Google Scholar
Bachmann, T. and Wickelgren, K., $\mathbb {A}^1$-Euler classes: six functors formalisms, dualities, integrality, and linear subspaces of complete intersections, Preprint (2002), arXiv:2002.01848.Google Scholar
Barge, J. and Morel, F., Groupe de Chow des cycles orientés et classe d'Euler des fibrés vectoriels, C. R. Acad. Sci. Paris Sér. I Math. 330 (2000), 287–290; MR 1753295.CrossRefGoogle Scholar
Basu, S., Lerario, A., Lundberg, E. and Peterson, C., Random fields and the enumerative geometry of lines on real and complex hypersurfaces, Math. Ann. 374 (2019), 1773–1810; MR 3985123.CrossRefGoogle Scholar
Beauville, A., Une notion de résidu en géométrie analytique, in Séminaire Pierre Lelong (Analyse). Année 1970, Lecture Notes in Mathematics, vol. 205 (Springer, Berlin, 1971), 183–203; MR 0437796.CrossRefGoogle Scholar
Beauville, A., Finite subgroups of PGL2(K), in Vector bundles and complex geometry, Contemporary Mathematics, vol. 522 (American Mathematical Society, Providence, RI, 2010), 23–29; MR 2681719.CrossRefGoogle Scholar
Benedetti, R. and Silhol, R., Spin and Pin structures, immersed and embedded surfaces and a result of Segre on real cubic surface, Topology 34 (1995), 651–678.CrossRefGoogle Scholar
Bhatwadekar, S. M., Das, M. K. and Mandal, S., Projective modules over smooth real affine varieties, Invent. Math. 166 (2006), 151–184; MR 2242636.CrossRefGoogle Scholar
Bhatwadekar, S. M. and Sridharan, R., Zero cycles and the Euler class groups of smooth real affine varieties, Invent. Math. 136 (1999), 287–322; MR 1688449.CrossRefGoogle Scholar
Bhatwadekar, S. M. and Sridharan, R., The Euler class group of a Noetherian ring, Compos. Math. 122 (2000), 183–222; MR 1775418.CrossRefGoogle Scholar
Cayley, A., On the triple tangent planes of surfaces of the third order, Cambridge Dublin Math. J. 4 (1849), 118–138.Google Scholar
Cazanave, C., Algebraic homotopy classes of rational functions, Ann. Sci. Éc. Norm. Supér. (4) 45 (2012), 511–534 (2013); MR 3059240.CrossRefGoogle Scholar
Conner, P. E. and Perlis, R., A survey of trace forms of algebraic number fields, Series in Pure Mathematics, vol. 2 (World Scientific, Singapore, 1984); MR 761569.CrossRefGoogle Scholar
Eisenbud, D., An algebraic approach to the topological degree of a smooth map, Bull. Amer. Math. Soc. (N.S.) 84 (1978), 751–764; MR 0494226 (58 $\#$13137).CrossRefGoogle Scholar
Eisenbud, D. and Levine, H. I., An algebraic formula for the degree of a $C^{\infty }$ map germ, Ann. of Math. (2) 106 (1977), 19–44, with an appendix by B. Teissier, “Sur une inégalité à la Minkowski pour les multiplicités”; MR 0467800 (57 $\#$7651).CrossRefGoogle Scholar
Fasel, J., Groupes de Chow-Witt, Mém. Soc. Math. Fr. (N.S.) 113 (2008); MR 2542148.Google Scholar
Fasel, J., Lectures on Chow-Witt groups, in Motivic homotopy theory and refined enumerative geometry, Contemporary Mathematics, vol. 745 (American Mathematical Society, Providence, RI, 2020), 83–121; MR 4071213.CrossRefGoogle Scholar
Finashin, S. and Kharlamov, V., Abundance of real lines on real projective hypersurfaces, Int. Math. Res. Not. IMRN 2013 (2013), 3639–3646; MR 3090704.CrossRefGoogle Scholar
Finashin, S. and Kharlamov, V., Abundance of 3-planes on real projective hypersurfaces, Arnold Math. J. 1 (2015), 171–199; MR 3370064.CrossRefGoogle Scholar
Grigor‘ev, D. J. and Ivanov, N. V., On the Eisenbud-Levine formula over a perfect field, Dokl. Akad. Nauk SSSR 252 (1980), 24–27; MR 572114.Google Scholar
Grothendieck, A. and Dieudonné, J. A., Eléments de géométrie algébrique. I, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 166 (Springer, Berlin, 1971); MR 3075000.Google Scholar
Hirschfeld, J. W. P., Finite projective spaces of three dimensions, Oxford Mathematical Monographs (Clarendon Press, Oxford, 1985); MR 840877.Google Scholar
Horev, A. and Solomon, J. P., The open Gromov–Witten–Welschinger theory of blowups of the projective plane, Preprint (2012), arXiv:1210.4034.Google Scholar
Hoyois, M., A quadratic refinement of the Grothendieck-Lefschetz-Verdier trace formula, Algebr. Geom. Topol. 14 (2014), 3603–3658; MR 3302973.CrossRefGoogle Scholar
Kass, J. L. and Wickelgren, K., The class of Eisenbud-Khimshiashvili-Levine is the local ${\boldsymbol {A}}^1$-Brouwer degree, Duke Math. J. 168 (2019), 429–469; MR 3909901.CrossRefGoogle Scholar
Khimshiashvili, G. N., The local degree of a smooth mapping, Sakharth. SSR Mecn. Akad. Moambe 85 (1977), 309–312; MR 0458467 (56 $\#$16670).Google Scholar
Knus, M.-A., Quadratic and Hermitian forms over rings, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 294 (Springer, Berlin, 1991), with a foreword by I. Bertuccioni; MR 1096299 (92i:11039).CrossRefGoogle Scholar
Lam, T. Y., Introduction to quadratic forms over fields, Graduate Studies in Mathematics, vol. 67 (American Mathematical Society, Providence, RI, 2005); MR 2104929.Google Scholar
Lam, T. Y., Serre's problem on projective modules, Springer Monographs in Mathematics (Springer, Berlin, 2006); MR 2235330.CrossRefGoogle Scholar
Levine, M., The intrinsic stable normal cone, Preprint (2017), arXiv:1703.03056.Google Scholar
Levine, M., Aspects of enumerative geometry with quadratic forms, Doc. Math., to appear. Preprint (2017), arXiv:1703.03049v1.Google Scholar
Levine, M., Toward an algebraic theory of Welschinger invariants, Preprint (2018), arXiv:1808.02238.Google Scholar
Levine, M., Motivic Euler characteristics and Witt-valued characteristic classes, Nagoya Math. J. 236 (2019), 251–310.CrossRefGoogle Scholar
Mandal, S. and Sridharan, R., Euler classes and complete intersections, J. Math. Kyoto Univ. 36 (1996), 453–470; MR 1417820.Google Scholar
McKean, S., An arithmetic enrichment of Bézout's Theorem, Math. Ann. 379 (2021), 633–660.CrossRefGoogle Scholar
Morel, F., $\Bbb A^1$-algebraic topology over a field, Lecture Notes in Mathematics, vol. 2052 (Springer, Berlin, 2012); MR 2934577.CrossRefGoogle Scholar
Okonek, C. and Teleman, A., Intrinsic signs and lower bounds in real algebraic geometry, J. Reine Angew. Math. 688 (2014), 219–241; MR 3176620.Google Scholar
Okonek, C. and Teleman, A., A wall-crossing formula for degrees of real central projections, Internat. J. Math. 25 (2014), 1450038; MR 3195554.CrossRefGoogle Scholar
Pauli, S., Quadratic types and the dynamic Euler number of lines on a quintic threefold, Preprint (2020), arXiv:2006.12089.Google Scholar
Scharlau, W., Quadratic reciprocity laws, J. Number Theory 4 (1972), 78–97; MR 292753.CrossRefGoogle Scholar
Scheja, G. and Storch, U., Über Spurfunktionen bei vollständigen Durchschnitten, J. Reine Angew. Math. 278/279 (1975), 174–190; MR 0393056 (52 $\#$13867).Google Scholar
Scheja, G. and Storch, U., Residuen bei vollständigen Durchschnitten, Math. Nachr. 91 (1979), 157–170; MR 563607.CrossRefGoogle Scholar
Revêtements étales et groupe fondamental, Séminaire de géométrie algébrique du Bois Marie 1960–61 (SGA 1), Documents Mathématiques (Paris), vol. 3 (Société Mathématique de France, Paris, 2003), directed by A. Grothendieck, with two papers by M. Raynaud. Updated and annotated reprint of the 1971 original [Lecture Notes in Mathematics, vol. 224, Springer, Berlin; MR 0354651 (50 $\#$7129)]; MR 2017446 (2004g:14017)Google Scholar
Solomon, J. P., Intersection theory on the moduli space of holomorphic curves with Lagrangian boundary conditions, PhD thesis, Massachusetts Institute of Technology, Cambridge, MA (2006), https://arxiv.org/abs/math/0606429.Google Scholar
Srinivasan, P. and Wickelgren, K., An arithmetic count of the lines meeting four lines in $\mathbb{P}^3$, Trans. Amer. Math. Soc., to appear. Preprint (2018), arXiv:1810.03503; with an appendix by B. Kadets, P. Srinivasan, A. A. Swaminathan, L. Taylor and D. Tseng.Google Scholar
The Stacks Project Authors, Stacks project (2017), http://stacks.math.columbia.edu.Google Scholar
Wendt, M., Schubert calculus in Chow–Witt rings of Grassmannians, in Motivic homotopy theory and refined enumerative geometry, Contemporary Mathematics, vol. 745 (American Mathematical Society, Providence, RI, 2020), 217–267; MR 4071212.CrossRefGoogle Scholar