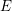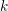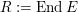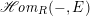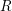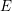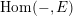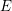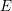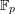1 Introduction
Let
$E$
be an elliptic curve over a field
$k$
. Let
$R:=\operatorname{End}E$
. We would like to classify all abelian varieties isogenous to a power of
$E$
. There is a functor
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
that takes as input a finitely presented (f.p.) left
$R$
-module
$M$
and produces a commutative group scheme. (This functor appears in articles by Giraud [Reference GiraudGir68, §1] and Waterhouse [Reference WaterhouseWat69, Appendix], and is attributed by the former to Serre and Tate; we will give a self-contained exposition in § 4.1.) We will prove that, when restricted to torsion-free modules, it becomes a fully faithful functor of additive categories
$$\begin{eqnarray}\displaystyle \mathscr{H}\!\mathit{om}_{R}(-,E): & & \displaystyle \{\text{f.p. torsion-free left }R\text{-modules}\}^{\operatorname{opp}}\nonumber\\ \displaystyle & & \displaystyle \longrightarrow \{\text{abelian varieties isogenous to a power of }E\}.\end{eqnarray}$$
In the other direction, we have a functor
$$\begin{eqnarray}\displaystyle \operatorname{Hom}(-,E): & & \displaystyle \{\text{abelian varieties isogenous to a power of }E\}\nonumber\\ \displaystyle & & \displaystyle \longrightarrow \{\text{f.p. torsion-free left }R\text{-modules}\}^{\operatorname{opp}}\end{eqnarray}$$
that provides the inverse on the essential image of (1). These are useful because the modules can be classified for each possible
$R$
.
We find necessary and sufficient conditions on
$E$
for (1) and (2) to be equivalences of categories. For simplicity, in this introduction we state the answer only for elliptic curves over finite fields.
Theorem 1.1. Let
$E$
be an elliptic curve over a finite field
$k=\mathbb{F}_{q}$
. Let
$R:=\operatorname{End}E$
. Let
$\unicode[STIX]{x1D70B}\in R$
be the
$q$
-power Frobenius endomorphism. Then (1) and (2) are equivalences of categories if and only if one of the following holds:
–
$E$
is ordinary and
$\mathbb{Z}[\unicode[STIX]{x1D70B}]=R$
;–
$E$
is supersingular,
$k=\mathbb{F}_{p}$
, and
$\mathbb{Z}[\unicode[STIX]{x1D70B}]=R$
; or–
$E$
is supersingular,
$k=\mathbb{F}_{p^{2}}$
, and
$R$
is of rank
$4$
over
$\mathbb{Z}$
.
Theorem 1.1 is close to many results in the literature. Waterhouse [Reference WaterhouseWat69] proves many results relating the isogeny class of an elliptic curve
$E$
to the ideal classes of
$\operatorname{End}E$
, and he also considers such issues when
$E$
is replaced by an abelian variety. An analogue of Theorem 1.1 with the functors
$\mathscr{H}\!\mathit{om}$
and
$\operatorname{Hom}(-,E)$
replaced by similarly defined functors
$\otimes$
and
$\operatorname{Hom}(E,-)$
is proved in Serre’s appendix to [Reference LauterLau02] in the case where
$\mathbb{Z}[\unicode[STIX]{x1D70B}]$
is the maximal order in an imaginary quadratic field (in this case,
$R=\mathbb{Z}[\unicode[STIX]{x1D70B}]$
necessarily). Other cases are handled in [Reference Shioda and MitaniSM74], [Reference LangeLan75], [Reference SchoenSch92], and especially Kani’s work [Reference KaniKan11]; although these works do not define the functor
$\mathscr{H}\!\mathit{om}$
, they too classify all abelian varieties isogenous to a power of
$E$
in the case where
$E$
is ordinary and
$\operatorname{rk}R=2$
(see [Reference KaniKan11, Theorems 1, 2, and 3]). In fact, at one point (in the proof of our Theorem 4.8(a)), we make use of one of the easier results of [Reference KaniKan11].
The category of all ordinary abelian varieties over a finite field is equivalent to the category of Deligne modules [Reference DeligneDel69], which are f.p. torsion-free
$\mathbb{Z}$
-modules provided with an endomorphism that corresponds to the Frobenius. The ordinary case of Theorem 1.1 could be deduced from Deligne’s equivalence. For a prime ground field
$\mathbb{F}_{p}$
, Yu [Reference YuYu12, Theorem 3.1] and (in a stronger form) Centeleghe and Stix [Reference Centeleghe and StixCS15] extended Deligne’s equivalence to a category including most non-ordinary abelian varieties. For suitable abelian varieties
$B$
over
$\mathbb{F}_{p}$
, this leads to a classification of the quotients of powers of
$B$
; in particular, when
$B$
is simple, these quotients are the abelian varieties isogenous to a power of
$B$
. Centeleghe and Stix did not mention the functor
$\mathscr{H}\!\mathit{om}_{R}(-,B)$
, but in § 8 we prove that a functor they used is isomorphic to
$\mathscr{H}\!\mathit{om}_{R}(-,B)$
. Combining their work with ours, we can rewrite their classification in terms of the functor
$\mathscr{H}\!\mathit{om}_{R}(-,B)$
. In particular, this yields a second proof of Theorem 1.1 in the case where the ground field
$k$
is
$\mathbb{F}_{p}$
. Our first proof, although only for elliptic curves, applies also to non-ordinary elliptic curves over
$\mathbb{F}_{p^{n}}$
for
$n>1$
and to elliptic curves over infinite fields (see Theorems 7.1 and 7.7, for example). It includes the quaternionic endomorphism case, and also determines exactly when the functors above give an equivalence.
Let us now outline the rest of the paper. Section 2 introduces notation to be used. If
$R$
is the endomorphism ring of an elliptic curve, then
$R$
is
$\mathbb{Z}$
, an imaginary quadratic order, or a maximal quaternionic order; § 3 reviews the classification of f.p. torsion-free left
$R$
-modules in each case, and in a little more generality. Section 4 introduces the two functors above and proves their basic properties; in particular it is shown that applying
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
to torsion-free modules produces abelian varieties isogenous to a power of
$E$
. Moreover, § 4.3 relates duality of modules to duality of abelian varieties. Section 5 proves that, when
$E$
is a supersingular elliptic curve over
$\mathbb{F}_{p^{2}}$
with
$\operatorname{rk}\operatorname{End}E=4$
, the functors (1) and (2) are equivalences of categories, so that there is a clean classification of abelian varieties isogenous to a power of
$E$
. In preparation for the other cases, § 6 defines the notion of a kernel subgroup, and shows that the functors (1) and (2) are equivalences of categories if and only if every finite subgroup scheme of every power of
$E$
is a kernel subgroup. All this is combined in § 7, which gives a complete answer to the question of when (1) and (2) are equivalences of categories. Section 8 contains the argument involving the work of Centeleghe and Stix for certain abelian varieties of higher dimension over
$\mathbb{F}_{p}$
.
2 Notation
Let
$R$
be a noetherian integral domain. Let
$K=\operatorname{Frac}R$
. The torsion submodule of an
$R$
-module
$M$
is
$$\begin{eqnarray}M_{\operatorname{tors}}:=\{m\in M:rm=0\text{ for some nonzero }r\in R\}.\end{eqnarray}$$
Call
$M$
torsion-free if
$M_{\operatorname{tors}}=0$
. Call a submodule
$N$
of
$M$
(or an injection
$N\rightarrow M$
) saturated if the cokernel of
$N\rightarrow M$
is torsion-free. Given a f.p.
$R$
-module
$M$
, define its rank as
$\operatorname{rk}M:=\dim _{K}(K\otimes _{R}M)$
. The notion of rank extends to f.p. left modules over a subring
$R$
in a division algebra
$K$
.
If
$k$
is a field, let
$\overline{k}$
be an algebraic closure of
$k$
, let
$k_{s}$
be the separable closure of
$k$
in
$\overline{k}$
, and let
${\mathcal{G}}_{k}:=\operatorname{Gal}(k_{s}/k)$
. If
$G$
is a finite group scheme over a field
$k$
, its order is
$\#G:=\dim _{k}\unicode[STIX]{x1D6E4}(G,\mathscr{O}_{G})$
.
Let
$A$
be a commutative group scheme over a field
$k$
. Then
$\operatorname{End}A$
denotes its endomorphism ring as a commutative group scheme over
$k$
, i.e., the ring of endomorphisms defined over
$k$
; an analogous convention applies to
$\operatorname{Hom}$
. If
$\unicode[STIX]{x1D706}\in \operatorname{End}A$
, then
$A[\unicode[STIX]{x1D706}]:=\ker \unicode[STIX]{x1D706}$
denotes the group scheme kernel of
$A\stackrel{\unicode[STIX]{x1D706}}{\rightarrow }A$
. In particular, if
$n\in \mathbb{Z}_{{>}0}$
, then
$A[n]$
is the group scheme kernel of
$A\stackrel{n}{\rightarrow }A$
. If
$\ell$
is a prime not equal to
$\operatorname{char}k$
, then the
$\ell$
-adic Tate module of
$A$
is
$$\begin{eqnarray}T_{\ell }A:=\underset{e}{\varprojlim }\,A[\ell ^{e}](k_{s}).\end{eqnarray}$$
If
$X$
is a scheme over a field
$k$
of characteristic
$p>0$
, and
$q$
is a power of
$p$
, let
$\unicode[STIX]{x1D70B}_{X,q}:X\rightarrow X^{(q)}$
be the
$q$
-power Frobenius morphism; if
$k=\mathbb{F}_{q}$
, then let
$\unicode[STIX]{x1D70B}_{X}$
be
$\unicode[STIX]{x1D70B}_{X,q}:X\rightarrow X$
.
Recall that the essential image of a functor
$F:{\mathcal{C}}\rightarrow {\mathcal{D}}$
consists of the objects of
${\mathcal{D}}$
isomorphic to
$FC$
for some
$C\in {\mathcal{C}}$
; from now on, we call this simply the image of
$F$
.
3 Classifying torsion-free modules
3.1 Dedekind domains
Suppose that
$R$
is a Dedekind domain. Finitely presented (henceforth denoted f.p.) torsion-free
$R$
-modules can be completely classified, as is well known [Reference ReinerRei03, Theorem 4.13]. To describe the result, we need the notion of determinant of a module. Given a torsion-free
$R$
-module
$M$
of rank
$r$
, its determinant
$\det M:=\bigwedge ^{r}M$
is a f.p. torsion-free
$R$
-module of rank
$1$
; sometimes we identify
$\det M$
with its class in
$\operatorname{Pic}R$
. For example, if
$M=I_{1}\oplus \cdots \oplus I_{r}$
, where each
$I_{j}$
is a nonzero ideal of
$R$
, then
$\operatorname{rk}M=r$
and
$$\begin{eqnarray}\det M\;\simeq \;I_{1}\underset{R}{\otimes }\cdots \underset{R}{\otimes }I_{r}\;\simeq \;I_{1}\cdots I_{r}\quad (\text{the product ideal in }R).\end{eqnarray}$$
Theorem 3.1.
(a) A f.p.
$R$
-module is torsion-free if and only if it is projective.(b) Every f.p. projective
$R$
-module is isomorphic to a finite direct sum of invertible ideals.(c) The isomorphism type of a f.p. projective
$R$
-module is determined by its rank and determinant.(d) Every pair
$(r,c)\in \mathbb{Z}_{{>}0}\times \operatorname{Pic}R$
arises as the rank and determinant of a nonzero f.p. projective
$R$
-module
$M$
; one representative is
$M:=R^{r-1}\oplus I$
where
$[I]=c$
.
3.2 Quadratic orders
For a general order in a Dedekind domain, the structure theory of torsion-free f.p. modules is wild. Fortunately, for quadratic orders there is a theory that is only slightly more complicated than that for Dedekind domains. Recall that if
$R_{\max }$
is the ring of integers in a quadratic field
$K$
, then every order in
$K$
is of the form
$R_{f}:=\mathbb{Z}+fR_{\max }$
for a positive integer
$f$
called the conductor. The orders containing
$R_{f}$
are the orders
$R_{g}$
for
$g|f$
.
Theorem 3.2. Let
$R$
be a quadratic order, i.e., an order in a degree
$2$
extension
$K$
of
$\mathbb{Q}$
. Let
$M$
be a f.p. torsion-free
$R$
-module.
(i) There exists a unique chain of orders
$R_{1}\subseteq \cdots \subseteq R_{n}$
between
$R$
and
$K$
and invertible ideals
$I_{1},\ldots ,I_{n}$
of
$R_{1},\ldots ,R_{n}$
, respectively, such that
$M\simeq I_{1}\oplus \cdots \oplus I_{n}$
as an
$R$
-module.(ii) The
$I_{i}$
are not unique, but their product
$I_{1}\cdots I_{n}$
is an invertible
$R_{n}$
-ideal whose class
$[M]\in \operatorname{Pic}R_{n}$
depends only on
$M$
.(iii) The isomorphism type of
$M$
is uniquely determined by the chain
$R_{1}\subseteq \cdots \subseteq R_{n}$
and the class
$[M]\in \operatorname{Pic}R_{n}$
.
Proof. See [Reference Borevič and FaddeevBF60]. For generalizations to other integral domains, see [Reference BassBas63, §7], [Reference Borevič and FaddeevBF65], [Reference LevyLev85], and the survey article [Reference SalceSal02]. ◻
3.3 Maximal orders in quaternion algebras
Let
$B$
be a quaternion division algebra over
$\mathbb{Q}$
. Let
${\mathcal{O}}$
be a maximal order in
$B$
. Suppose that
$M$
is a f.p. left
${\mathcal{O}}$
-module. The abelian group
$B\otimes _{{\mathcal{O}}}M$
inherits a left
$B$
-module structure from
$B$
; it is a free left
$B$
-module by [Reference BourbakiBou70, II, §7, Théorème 1]. The nonnegative integer
$\operatorname{rk}M$
is the dimension of the left
$B$
-vector space
$B\otimes _{{\mathcal{O}}}M$
; then
$\operatorname{rk}M=\frac{1}{4}\operatorname{rk}_{\mathbb{Z}}M$
. Call
$M$
torsion-free if the natural map
$M\rightarrow B\otimes _{{\mathcal{O}}}M$
is an injection, or equivalently, if
$M$
is torsion-free as a
$\mathbb{Z}$
-module.
The classification of f.p. torsion-free left
${\mathcal{O}}$
-modules is similar to the classification over a Dedekind domain, and even simpler in ranks at least
$2$
.
Theorem 3.3.
(a) A f.p. left
${\mathcal{O}}$
-module is torsion-free if and only if it is projective.(b) Every f.p. projective left
${\mathcal{O}}$
-module is isomorphic to a finite direct sum of ideals.(c) A f.p. projective left
${\mathcal{O}}$
-module of rank at least
$2$
is free.
Proof.
(a) See [Reference ReinerRei03, Corollary 21.5].
(b) This follows from the final statement of [Reference ReinerRei03, Corollary 21.5].
(c) This is a classical result due to Eichler [Reference EichlerEic38]; see also [Reference Shioda and LønstedShi79, Theorem 3.5]. ◻
4 Categorical constructions
4.1 A functor to an abelian category
We recall the following general construction (cf. [Reference GiraudGir68, §1], [Reference WaterhouseWat69, Appendix], or [Reference SerreSer85, pp. 50–51]). Fix an abelian category
${\mathcal{C}}$
, an object
$E\in {\mathcal{C}}$
, a ring
$R$
, and a ring homomorphism
$R\rightarrow \operatorname{End}E$
. For each f.p. left
$R$
-module
$M$
, choose a presentation
$$\begin{eqnarray}R^{m}\rightarrow R^{n}\rightarrow M\rightarrow 0.\end{eqnarray}$$
If we view
$R^{m}$
and
$R^{n}$
as spaces of row vectors, then the
$R$
-module homomorphism
$R^{m}\rightarrow R^{n}$
is represented by right-multiplication by some matrix
$X\in \operatorname{M}_{m,n}(R)$
. Since
$R$
acts on
$E$
, left-multiplication by
$X$
defines a morphism
$E^{n}\rightarrow E^{m}$
, whose kernel we call
$A$
:
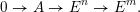$$\begin{eqnarray}0\rightarrow A\rightarrow E^{n}\rightarrow E^{m}.\end{eqnarray}$$
For any
$C\in {\mathcal{C}}$
, applying
$\operatorname{Hom}(C,-)$
yields an exact sequence
$$\begin{eqnarray}0\rightarrow \operatorname{Hom}(C,A)\rightarrow \operatorname{Hom}(C,E)^{n}\rightarrow \operatorname{Hom}(C,E)^{m}.\end{eqnarray}$$
On the other hand, applying
$\operatorname{Hom}_{R}(-,\operatorname{Hom}(C,E))$
to (3) yields an exact sequence
$$\begin{eqnarray}0\rightarrow \operatorname{Hom}_{R}(M,\operatorname{Hom}(C,E))\rightarrow \operatorname{Hom}(C,E)^{n}\rightarrow \operatorname{Hom}(C,E)^{m}.\end{eqnarray}$$
Comparing the previous two sequences yields an isomorphism
$$\begin{eqnarray}\operatorname{Hom}(C,A)\simeq \operatorname{Hom}_{R}(M,\operatorname{Hom}(C,E)),\end{eqnarray}$$
and it is functorial in
$C$
. This gives a presentation-independent description of
$A$
up to isomorphism as an object of
${\mathcal{C}}$
representing the functor
$\operatorname{Hom}_{R}(M,\operatorname{Hom}(-,E)):{\mathcal{C}}\rightarrow \text{}\text{Sets}$
. Define
$\mathscr{H}\!\mathit{om}_{R}(M,E):=A$
.
An
$R$
-module homomorphism
$M\rightarrow M^{\prime }$
induces a homomorphism
$$\begin{eqnarray}\operatorname{Hom}_{R}(M^{\prime },\operatorname{Hom}(C,E))\rightarrow \operatorname{Hom}_{R}(M,\operatorname{Hom}(C,E))\end{eqnarray}$$
for each
$C\in {\mathcal{C}}$
, functorially in
$C$
, so by Yoneda’s lemma it induces also a morphism between the representing objects
$\mathscr{H}\!\mathit{om}_{R}(M^{\prime },E)\rightarrow \mathscr{H}\!\mathit{om}_{R}(M,E)$
. Thus we obtain a functor
$$\begin{eqnarray}\mathscr{H}\!\mathit{om}_{R}(-,E):\{\text{f.p. left }R\text{-modules}\}^{\operatorname{opp}}\longrightarrow {\mathcal{C}}.\end{eqnarray}$$
If
$0\rightarrow M_{1}\rightarrow M_{2}\rightarrow M_{3}$
is an exact sequence of f.p. left
$R$
-modules, then, for each
$C\in {\mathcal{C}}$
,
$$\begin{eqnarray}0\rightarrow \operatorname{Hom}_{R}(M_{1},\operatorname{Hom}(C,E))\rightarrow \operatorname{Hom}_{R}(M_{2},\operatorname{Hom}(C,E))\rightarrow \operatorname{Hom}_{R}(M_{3},\operatorname{Hom}(C,E))\end{eqnarray}$$
is exact. This implies that the sequence of representing objects
$$\begin{eqnarray}0\rightarrow \mathscr{H}\!\mathit{om}_{R}(M_{1},E)\rightarrow \mathscr{H}\!\mathit{om}_{R}(M_{2},E)\rightarrow \mathscr{H}\!\mathit{om}_{R}(M_{3},E)\end{eqnarray}$$
is exact. That is, the functor
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is left exact.
Remark 4.1. Following Serre’s appendix to [Reference LauterLau02], one can also define a functor
$$\begin{eqnarray}-\otimes _{R}E:\{\text{f.p. right }R\text{-modules}\}\longrightarrow {\mathcal{C}}.\end{eqnarray}$$
Namely, given a f.p. right
$R$
-module
$M$
, choose a presentation
$$\begin{eqnarray}R^{m}\rightarrow R^{n}\rightarrow M\rightarrow 0,\end{eqnarray}$$
and define
$M\otimes _{R}E$
as the cokernel of
$E^{m}\rightarrow E^{n}$
.
4.2 The functor for an elliptic curve produces abelian varieties
The category of commutative proper group schemes over a field
$k$
is an abelian category (the hardest part of this statement is the existence of cokernels, which is [Reference GrothendieckGro61, Corollaire 7.4]). From now on, we assume that
${\mathcal{C}}$
is this category.
Proposition 4.2. Let
$M$
be an
$R$
-module. Let
$A:=\mathscr{H}\!\mathit{om}_{R}(M,E)$
. For every
$k$
-algebra
$L$
, we have
$A(L)\simeq \operatorname{Hom}_{R}(M,E(L))$
.
Proof. Taking
$L$
-points of (4) yields an exact sequence
$$\begin{eqnarray}0\rightarrow A(L)\rightarrow E(L)^{n}\rightarrow E(L)^{m}.\end{eqnarray}$$
On the other hand, applying
$\operatorname{Hom}_{R}(-,E(L))$
to (3) yields an exact sequence
$$\begin{eqnarray}0\rightarrow \operatorname{Hom}_{R}(M,E(L))\rightarrow E(L)^{n}\rightarrow E(L)^{m}.\end{eqnarray}$$
The maps
$E(L)^{n}\rightarrow E(L)^{m}$
in both sequences are the same, so the result follows.◻
Proposition 4.3. Let
$E$
be an abelian variety over a field
$k$
. Let
$R$
be a domain that is f.p. as a
$\mathbb{Z}$
-module. Let
$R\rightarrow \operatorname{End}E$
be a ring homomorphism. Let
$M$
be a f.p. left
$R$
-module. Let
$A:=\mathscr{H}\!\mathit{om}_{R}(M,E)$
. Then
$\dim A=(\operatorname{rk}M)(\dim E)$
.
Proof. For any
$n\geqslant 1$
, the presentation
$R\stackrel{n}{\rightarrow }R\rightarrow R/nR\rightarrow 0$
shows that
$\mathscr{H}\!\mathit{om}_{R}(R/nR,E)\simeq E[n]$
. If
$M$
is torsion, then it is a quotient of
$(R/nR)^{m}$
for some
$m,n\geqslant 1$
; then
$A\subseteq E[n]^{m}$
, so
$A$
is finite.
In general, let
$r=\operatorname{rk}M$
. There is an exact sequence
$$\begin{eqnarray}0\rightarrow R^{r}\rightarrow M\rightarrow T\rightarrow 0\end{eqnarray}$$
for some torsion module
$T$
; this yields
$$\begin{eqnarray}0\rightarrow \mathscr{H}\!\mathit{om}_{R}(T,E)\rightarrow A\rightarrow E^{r}.\end{eqnarray}$$
By the previous paragraph,
$\mathscr{H}\!\mathit{om}_{R}(T,E)$
is finite, so
$\dim A\leqslant r\dim E$
. There exists a nonzero
$\unicode[STIX]{x1D70C}\in R$
such that
$\unicode[STIX]{x1D70C}T=0$
. Since
$R$
is f.p. as a
$\mathbb{Z}$
-module, it follows that there exists a positive integer
$n$
such that
$nT=0$
. Then
$R^{r}\stackrel{n}{\rightarrow }R^{r}$
factors as
$R^{r}{\hookrightarrow}M\rightarrow R^{r}$
, which induces
$E^{r}\rightarrow A\rightarrow E^{r}$
whose composition is multiplication by
$n$
, which is surjective. Thus
$A\rightarrow E^{r}$
is surjective, so
$\dim A\geqslant r\dim E$
. Hence
$\dim A=r\dim E$
.◻
If
$E$
is an elliptic curve, and
$I$
is a subset of
$\operatorname{End}E$
, let
$E[I]:=\bigcap _{\unicode[STIX]{x1D6FC}\in I}\ker \unicode[STIX]{x1D6FC}$
.
Theorem 4.4. Let
$E$
be an elliptic curve over a field
$k$
. Let
$R$
be a saturated subring of
$\operatorname{End}E$
(saturated as a
$\mathbb{Z}$
-module). Let
$M$
be a torsion-free f.p. left
$R$
-module. Let
$A:=\mathscr{H}\!\mathit{om}_{R}(M,E)$
. Then the following hold.
(a) The group scheme
$A$
is an abelian variety isogenous to a power of
$E$
.(b) The functor
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is exact.(c) If
$f:E^{r}\rightarrow E^{s}$
is a homomorphism arising from applying
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
to an
$R$
-homomorphism
$g:R^{s}\rightarrow R^{r}$
, then the image of
$f$
is isomorphic to
$\mathscr{H}\!\mathit{om}_{R}(N,E)$
for some f.p. torsion-free
$R$
-module
$N\subseteq R^{r}$
. (Moreover, if
$R=\operatorname{End}E$
, then every homomorphism
$f:E^{r}\rightarrow E^{s}$
arises from some
$g$
.)(d) If
$I$
is a nonzero left
$R$
-ideal, then
$\mathscr{H}\!\mathit{om}_{R}(R/I,E)\simeq E[I]$
and
$\mathscr{H}\!\mathit{om}_{R}(I,E)\simeq E/E[I]$
.(e) If
$T$
is an
$R$
-module that is finite as a set, then
$\mathscr{H}\!\mathit{om}_{R}(T,E)$
is a finite group scheme of order
$(\#T)^{2/\text{rk}\,R}$
.(f) If
$n\in \mathbb{Z}_{{>}0}$
, then
$A[n]\simeq \mathscr{H}\!\mathit{om}_{R}(M,E[n])$
, where the latter is defined by using the induced ring homomorphism
$R\rightarrow \operatorname{End}E[n]$
.(g) If
$\ell$
is a prime not equal to
$\operatorname{char}k$
, then
$T_{\ell }A\simeq \operatorname{Hom}_{R}(M,T_{\ell }E)$
.
Proof. (a) Let
$r=\operatorname{rk}M=\dim A$
. The proof of Proposition 4.3 shows that
$A$
admits a surjection to
$E^{r}$
with finite kernel, so if
$A$
is an abelian variety, it is isogenous to
$E^{r}$
.
The ring
$R$
is either
$\mathbb{Z}$
, a quadratic order, or a maximal quaternionic order. In the first and third cases,
$M$
is projective of rank
$r$
over
$R$
(the quaternionic case is Theorem 3.3(a)); in other words,
$M$
is a direct summand of
$R^{n}$
for some
$n$
; thus
$A$
is a direct factor of
$E^{n}$
, so
$A$
is an abelian variety.
So suppose that
$R$
is a quadratic order. Let
$c$
be the conductor, i.e., the index of
$R$
in its integral closure. Let
$\ell$
denote a prime. If
$\ell \nmid c$
, then the semi-local ring
$R\otimes \mathbb{Z}_{(\ell )}$
is a Dedekind domain, but a semi-local Dedekind domain is a principal ideal domain, so
$M\otimes \mathbb{Z}_{(\ell )}$
is free of rank
$r$
over
$R\otimes \mathbb{Z}_{(\ell )}$
, and
$M/\ell M$
is free of rank
$r$
over
$R/\ell R$
.
We claim that
$A$
is smooth. This is automatic if
$\operatorname{char}k=0$
. So suppose that
$\operatorname{char}k=p>0$
. By [Reference WaterhouseWat69, Theorem 4.2], we have
$p\nmid c$
, so by the above,
$M/pM$
is free of rank
$r$
over
$R/pR$
. By Proposition 4.2, applying
$\operatorname{Hom}_{R}(M,-)$
to
$$\begin{eqnarray}0\longrightarrow \operatorname{Lie}E\longrightarrow E(k[\unicode[STIX]{x1D716}]/(\unicode[STIX]{x1D716}^{2}))\longrightarrow E(k)\longrightarrow 0\end{eqnarray}$$
yields
$$\begin{eqnarray}0\longrightarrow \operatorname{Hom}_{R}(M,\operatorname{Lie}E)\longrightarrow A(k[\unicode[STIX]{x1D716}]/(\unicode[STIX]{x1D716}^{2}))\longrightarrow A(k)\longrightarrow 0.\end{eqnarray}$$
Thus
$$\begin{eqnarray}\operatorname{Lie}A\simeq \operatorname{Hom}_{R}(M,\operatorname{Lie}E)\simeq \operatorname{Hom}_{R/pR}(M/pM,\operatorname{Lie}E)\simeq (\operatorname{Lie}E)^{r}.\end{eqnarray}$$
In particular,
$\dim \operatorname{Lie}A=r$
, so
$A$
is smooth.
Since
$A$
is also proper, it is an extension of a finite étale commutative group scheme
$\unicode[STIX]{x1D6F7}$
by an abelian variety
$B$
. The constructed surjection
$A\rightarrow E^{r}$
with finite kernel restricts to a homomorphism
$B\rightarrow E^{r}$
with finite kernel, and it must still be surjective since
$E^{r}$
does not have algebraic subgroups of finite index; thus
$B$
is isogenous to
$E^{r}$
. Since
$B(\overline{k})$
is divisible, the extension splits over
$\overline{k}$
. In particular, for each prime
$\ell$
,
$$\begin{eqnarray}\#A(\overline{k})[\ell ]=\#E(\overline{k})[\ell ]^{r}\#\unicode[STIX]{x1D6F7}[\ell ].\end{eqnarray}$$
On the other hand, Proposition 4.2 implies
$$\begin{eqnarray}A(\overline{k})[\ell ]=\operatorname{Hom}_{R}(M,E(\overline{k})[\ell ])=\operatorname{Hom}_{R/\ell R}(M/\ell M,E(\overline{k})[\ell ]).\end{eqnarray}$$
We claim that
$$\begin{eqnarray}\#A(\overline{k})[\ell ]=\#E(\overline{k})[\ell ]^{r}.\end{eqnarray}$$
If
$\ell \nmid c$
, then
$M/\ell M$
is free of rank
$r$
over
$R/\ell R$
, so (9) holds. Now suppose that
$\ell |c$
; in particular,
$\ell \neq p$
. Then
$R/\ell R\simeq \mathbb{F}_{\ell }[e]/(e^{2})$
. Every
$(R/\ell R)$
-module is a direct sum of copies of
$\mathbb{F}_{\ell }$
and
$\mathbb{F}_{\ell }[e]/(e^{2})$
. Since
$R$
is saturated in
$\operatorname{End}E$
and
$\ell \neq p$
, the homomorphisms
$$\begin{eqnarray}\frac{R}{\ell R}\longrightarrow \frac{\operatorname{End}E}{\ell (\operatorname{End}E)}\longrightarrow \operatorname{End}E(\overline{k})[\ell ]\end{eqnarray}$$
are injective. On the other hand,
$\#E(\overline{k})[\ell ]=\ell ^{2}=\#(R/\ell R)$
. The previous three sentences imply that
$E(\overline{k})[\ell ]$
is free of rank
$1$
over
$R/\ell R$
. The equality
$\#\operatorname{Hom}_{R/\ell R}(N,R/\ell R)=\#N$
holds for
$N=\mathbb{F}_{\ell }$
and
$N=\mathbb{F}_{\ell }[e]/(e^{2})$
, so it holds for every finite
$(R/\ell R)$
-module
$N$
, and in particular for
$M/\ell M$
. Thus (8) implies
$$\begin{eqnarray}\#A(\overline{k})[\ell ]=\#(M/\ell M)=\#(R/\ell R)^{r}=\#E(\overline{k})[\ell ]^{r};\end{eqnarray}$$
the middle equality holds since
$M$
and
$R^{r}$
are torsion-free
$\mathbb{Z}$
-modules of the same rank. Hence (9) holds for all
$\ell$
.
Comparing (7) and (9) shows that
$\#\unicode[STIX]{x1D6F7}[\ell ]=1$
for all
$\ell$
, so
$\unicode[STIX]{x1D6F7}$
is trivial. Thus
$A=B$
, an abelian variety.
(b) By Lemma 4.5 below, it suffices to show that if
$M\rightarrow P$
is an injection of modules with
$P$
projective, then
$\mathscr{H}\!\mathit{om}_{R}(P,E)\rightarrow \mathscr{H}\!\mathit{om}_{R}(M,E)$
is surjective. We have an exact sequence
$$\begin{eqnarray}0\longrightarrow \mathscr{H}\!\mathit{om}_{R}(P/M,E)\longrightarrow \mathscr{H}\!\mathit{om}_{R}(P,E)\longrightarrow \mathscr{H}\!\mathit{om}_{R}(M,E).\end{eqnarray}$$
By (a),
$\mathscr{H}\!\mathit{om}_{R}(P,E)$
and
$\mathscr{H}\!\mathit{om}_{R}(M,E)$
are abelian varieties, so the image
$I$
of
$\mathscr{H}\!\mathit{om}_{R}(P,E)\rightarrow \mathscr{H}\!\mathit{om}_{R}(M,E)$
is an abelian subvariety of
$\mathscr{H}\!\mathit{om}_{R}(M,E)$
. By Proposition 4.3,
$$\begin{eqnarray}\dim \mathscr{H}\!\mathit{om}_{R}(P,E)=\dim \mathscr{H}\!\mathit{om}_{R}(P/M,E)+\dim \mathscr{H}\!\mathit{om}_{R}(M,E),\end{eqnarray}$$
so
$\dim I=\dim \mathscr{H}\!\mathit{om}_{R}(M,E)$
. Thus
$I=\mathscr{H}\!\mathit{om}_{R}(M,E)$
; i.e.,
$\mathscr{H}\!\mathit{om}_{R}(P,E)\rightarrow \mathscr{H}\!\mathit{om}_{R}(M,E)$
is surjective.
(c) Since
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is exact, it transforms the co-image of
$g$
into the image of
$f$
. (Co-image equals image in any abelian category, though the proof above does not need this.)
(d) The proof of [Reference WaterhouseWat69, Proposition A.2] shows that
$\mathscr{H}\!\mathit{om}_{R}(R/I,E)\simeq E[I]$
(there
$R$
is equal to
$\operatorname{End}E$
, but this is not used). The proof of [Reference WaterhouseWat69, Proposition A.3] shows that
$E/E[I]$
is the connected component of
$\mathscr{H}\!\mathit{om}_{R}(I,E)$
, but
$\mathscr{H}\!\mathit{om}_{R}(I,E)$
is already connected, by (a).
(e) The function
$(\#T)^{2/\text{rk}\,R}$
of
$T$
is multiplicative in short exact sequences. So is the quantity
$\#\mathscr{H}\!\mathit{om}_{R}(T,E)$
, since
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is exact. Thus we may reduce to the case in which
$T$
is simple, i.e.,
$T\simeq R/I$
for some maximal ideal
$I$
. Then
$\mathscr{H}\!\mathit{om}_{R}(T,E)=E[I]$
by (d). We have
$I\supseteq \ell R$
for some prime
$\ell$
. If
$I=\ell R$
, then
$E[I]=E[\ell ]$
, which has order
$\ell ^{2}=\#(R/I)^{2/\text{rk}\,R}$
.
Now suppose that
$I\neq \ell R$
. If
$R$
has rank
$2$
, then
$\#(R/I)=\ell$
; if
$R$
has rank
$4$
, then
$\#(R/I)=\ell ^{2}$
. Choose
$f\in I\setminus \ell R$
; then
$f$
does not kill
$E[\ell ]$
, so
$E[I]\subsetneq E[\ell ]$
. Thus
$\#E[I]\leqslant \ell =\#(R/I)^{2/\text{rk}\,R}$
. Thus
$\#\mathscr{H}\!\mathit{om}_{R}(T,E)\leqslant (\#T)^{2/\text{rk}\,R}$
holds for each Jordan–Hölder factor of
$R/\ell R$
, but for
$T=R/\ell R$
equality holds, so all the inequalities must have been equalities.
(f) Start with the exact sequence
$$\begin{eqnarray}0\rightarrow E[n]\rightarrow E\stackrel{n}{\rightarrow }E.\end{eqnarray}$$
Given
$S\in {\mathcal{C}}$
, apply the left exact functors
$\operatorname{Hom}_{{\mathcal{C}}}(S,-)$
and then
$\operatorname{Hom}_{R}(M,-)$
; taken for all
$S$
, this produces an exact sequence of representable functors
$$\begin{eqnarray}0\longrightarrow \mathscr{H}\!\mathit{om}_{R}(M,E[n])\longrightarrow \mathscr{H}\!\mathit{om}_{R}(M,E)\stackrel{n}{\longrightarrow }\mathscr{H}\!\mathit{om}_{R}(M,E).\end{eqnarray}$$
Hence
$\mathscr{H}\!\mathit{om}_{R}(M,E[n])\simeq A[n]$
.
(g) We have
$$\begin{eqnarray}\displaystyle T_{\ell }A & := & \displaystyle \underset{e}{\varprojlim }\,A[\ell ^{e}](k_{s})\nonumber\\ \displaystyle & \simeq & \displaystyle \underset{e}{\varprojlim }\,\mathscr{H}\!\mathit{om}_{R}(M,E[\ell ^{e}])(k_{s})\quad \text{(by (f))}\nonumber\\ \displaystyle & \simeq & \displaystyle \underset{e}{\varprojlim }\,\operatorname{Hom}_{R}(M,E[\ell ^{e}](k_{s}))\quad (\text{by Proposition 4.2 with }E\text{ replaced by }E[\ell ^{e}])\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{Hom}_{R}\Bigl(M,\mathop{\varprojlim }\nolimits_{e}E[\ell ^{e}](k_{s})\Bigr)\nonumber\\ \displaystyle & =: & \displaystyle \operatorname{Hom}_{R}(M,T_{\ell }E).\square\nonumber\end{eqnarray}$$
The following was used in the proof of Theorem 4.4(b).
Lemma 4.5. Let
${\mathcal{C}}$
be an abelian category with enough projectives. Let
$F:{\mathcal{C}}^{\operatorname{opp}}\rightarrow {\mathcal{D}}$
be a left exact functor. Suppose that for each monomorphism
$M\rightarrow P$
with
$P$
projective, the morphism
$FP\rightarrow FM$
is an epimorphism. Then
$F$
is exact.
Proof. Given
$A\in {\mathcal{C}}$
, choose an epimorphism
$P\rightarrow A$
with
$P$
projective, and let
$K$
be the kernel. The sequence
$0\rightarrow K\rightarrow P\rightarrow A\rightarrow 0$
yields
$$\begin{eqnarray}0\rightarrow FA\rightarrow FP\rightarrow FK\rightarrow (R^{1}F)A\rightarrow (R^{1}F)P=0,\end{eqnarray}$$
and the hypothesis implies that
$FP\rightarrow FK$
is surjective, so
$(R^{1}F)A=0$
. This holds for all
$A$
, so
$F$
is exact.◻
Remark 4.6. The hypothesis that
$R$
is saturated in Theorem 4.4 cannot be dropped. For example, if
$E$
is an elliptic curve over
$\mathbb{C}$
with
$\operatorname{End}E=\mathbb{Z}[i]$
, and
$R$
is the subring
$\mathbb{Z}[2i]$
, then the
$R$
-module
$\mathbb{Z}[i]$
has a presentation
$$\begin{eqnarray}R\stackrel{\left(\begin{array}{@{}c@{}}2i\\ -2\end{array}\right)}{\longrightarrow }R^{2}\stackrel{\left(\begin{array}{@{}cc@{}}1 & i\end{array}\right)}{\longrightarrow }\mathbb{Z}[i]\longrightarrow 0,\end{eqnarray}$$
so by definition,
$$\begin{eqnarray}\mathscr{H}\!\mathit{om}_{R}(\mathbb{Z}[i],E)\;\simeq \;\ker \Bigl(E^{2}\stackrel{\left(\begin{array}{@{}cc@{}}2i & -2\end{array}\right)}{\longrightarrow }E\Bigr)\simeq E\times E[2],\end{eqnarray}$$
which is not an abelian variety. Moreover, applying
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
to the injection
$\mathbb{Z}[i]\stackrel{2}{\rightarrow }R$
yields a homomorphism
$E\rightarrow E\times E[2]$
, which is not surjective, so
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is not exact. Finally,
$\mathbb{Z}[i]$
is isomorphic as
$R$
-module to the
$R$
-ideal
$I:=2\mathbb{Z}[i]$
, so
$\mathscr{H}\!\mathit{om}_{R}(I,E)$
is not an abelian variety.
4.3 Duality of abelian varieties
Let
$E$
be an elliptic curve over a field
$k$
. Let
$R:=\operatorname{End}E$
. The Rosati involution, sending an endomorphism to its dual, is an isomorphism
$R\rightarrow R^{\operatorname{opp}}$
. If
$M$
is a left
$R$
-module, then
$M^{\ast }:=\operatorname{Hom}_{R}(M,R)$
(the group of homomorphisms of left
$R$
-modules) is a right
$R$
-module: given
$f\in M^{\ast }$
and
$r\in R$
, let
$f\cdot r$
be the composition
$M\stackrel{f}{\rightarrow }R\stackrel{r}{\rightarrow }R$
, where
$R\stackrel{r}{\rightarrow }R$
is right-multiplication by
$r$
. In other words,
$M^{\ast }$
is a left
$R^{\operatorname{opp}}$
-module, which we may reinterpret as a left
$R$
-module by using the Rosati involution. Moreover, if
$M$
is f.p., then it is finite over
$\mathbb{Z}$
, and then so is
$M^{\ast }$
. Also,
$M^{\ast }$
is torsion-free.
Given an abelian variety
$A$
, let
$A^{\vee }$
be the dual abelian variety. The following lets us understand the duals of abelian varieties arising from modules.
Theorem 4.7. Given a f.p. torsion-free left
$R$
-module
$M$
, we have
$$\begin{eqnarray}\mathscr{H}\!\mathit{om}_{R}(M,E)^{\vee }\simeq \mathscr{H}\!\mathit{om}_{R}(M^{\ast },E),\end{eqnarray}$$
functorially in
$M$
.
Proof. Let
$M$
be a f.p. torsion-free left
$R$
-module. Choose a presentation as in (3),
$$\begin{eqnarray}R^{m}\stackrel{X}{\longrightarrow }R^{n}\longrightarrow M\longrightarrow 0,\end{eqnarray}$$
in which the first homomorphism is right-multiplication by some
$X\in \operatorname{M}_{m\times n}(R)$
on row vectors. Apply
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
to obtain
$$\begin{eqnarray}0\longrightarrow A\longrightarrow E^{n}\stackrel{X}{\longrightarrow }E^{m},\end{eqnarray}$$
in which
$X$
now acts on the left. Taking dual abelian varieties yields
$$\begin{eqnarray}E^{m}\stackrel{X^{\dagger }}{\longrightarrow }E^{n}\longrightarrow A^{\vee }\longrightarrow 0,\end{eqnarray}$$
where
$X^{\dagger }\in \operatorname{M}_{n\times m}(R)$
is obtained from
$X$
by taking the transpose and applying the Rosati involution entrywise.
On the other hand, applying
$\operatorname{Hom}_{R}(-,R)$
to (10) yields an exact sequence of right
$R$
-modules
$$\begin{eqnarray}0\longrightarrow M^{\ast }\longrightarrow R^{n}\stackrel{X}{\longrightarrow }R^{m}\end{eqnarray}$$
involving left-multiplication by
$X$
on column vectors. This may be reinterpreted via the Rosati involution as an exact sequence of left
$R$
-modules
$$\begin{eqnarray}0\longrightarrow M^{\ast }\longrightarrow R^{n}\stackrel{X^{\dagger }}{\longrightarrow }R^{m}\end{eqnarray}$$
involving right-multiplication by
$X^{\dagger }$
on row vectors. Applying the exact functor
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
yields
$$\begin{eqnarray}E^{m}\stackrel{X^{\dagger }}{\longrightarrow }E^{n}\longrightarrow \mathscr{H}\!\mathit{om}_{R}(M^{\ast },E)\longrightarrow 0.\end{eqnarray}$$
Comparing with (11) yields an isomorphism
$$\begin{eqnarray}\mathscr{H}\!\mathit{om}_{R}(M^{\ast },E)\simeq A^{\vee }=\mathscr{H}\!\mathit{om}_{R}(M,E)^{\vee }.\end{eqnarray}$$
Given a homomorphism of f.p. torsion-free left
$R$
-modules
$M\stackrel{f}{\rightarrow }N$
, we can build a commutative diagram
and apply the constructions above to show that (12) is functorial in
$M$
.◻
4.4 The other Hom functor
Under the assumptions of Theorem 4.4 (b), we have a functor of additive categories
$$\begin{eqnarray}\displaystyle \mathscr{H}\!\mathit{om}_{R}(-,E): & & \displaystyle \{\text{f.p. torsion-free left }R\text{-modules}\}^{\operatorname{opp}}\nonumber\\ \displaystyle & & \displaystyle \longrightarrow \{\text{abelian varieties isogenous to a power of }E\},\nonumber\end{eqnarray}$$
as promised in the introduction. From now on,
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
denotes this functor, restricted to f.p. torsion-free left
$R$
-modules.
Given an abelian variety
$A$
over the same field as
$E$
, the abelian group
$\operatorname{Hom}(A,E)$
(the group of homomorphisms of abelian varieties) is a left
$(\operatorname{End}E)$
-module, and hence also a left
$R$
-module, and it is f.p. because it is f.p. over
$\mathbb{Z}$
[Reference MumfordMum70, p. 178, Corollary 1]. In fact, we get a functor in the opposite direction:
$$\begin{eqnarray}\displaystyle \operatorname{Hom}(-,E): & & \displaystyle \{\text{abelian varieties isogenous to a power of }E\}\nonumber\\ \displaystyle & & \displaystyle \longrightarrow \{\text{f.p. torsion-free left }R\text{-modules}\}^{\operatorname{opp}}.\nonumber\end{eqnarray}$$
For which elliptic curves
$E$
are
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
inverse equivalences of categories? If we start with the
$R$
-module
$R$
and apply
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and then
$\operatorname{Hom}(-,E)$
, we obtain
$\operatorname{End}E$
, so we should have
$R\simeq \operatorname{End}E$
as
$R$
-modules; then the only
$R$
-module endomorphisms of
$\operatorname{End}E$
are given by multiplication by elements of
$R$
, but multiplication by elements of
$\operatorname{End}E$
also give endomorphisms, so
$R=\operatorname{End}E$
. Thus we assume from now on that
$R=\operatorname{End}E$
.
Theorem 4.8. Let
$E$
be an elliptic curve over a field. Let
$R:=\operatorname{End}E$
. Then the following hold.
(a) The functor
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is fully faithful.(b) The functor
$\operatorname{Hom}(-,E)$
on the image of
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is an inverse to
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
.(c) The image of
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
consists exactly of the products of elliptic curves of the form
$\mathscr{H}\!\mathit{om}_{R}(I,E)$
for a nonzero left
$R$
-ideal
$I$
.
Proof. (a) The ring
$R$
is
$\mathbb{Z}$
, a quadratic order, or a maximal quaternionic order. By Theorem 3.1, Theorem 3.2(i), or Theorem 3.3(b), respectively, every f.p. torsion-free left
$R$
-module is a finite direct sum of nonzero left
$R$
-ideals. Thus, (a) follows if, for any two nonzero
$R$
-ideals
$I$
and
$J$
, the natural map
$$\begin{eqnarray}\operatorname{Hom}_{R}(J,I)\longrightarrow \operatorname{Hom}(\mathscr{H}\!\mathit{om}_{R}(I,E),\mathscr{H}\!\mathit{om}_{R}(J,E))\end{eqnarray}$$
is an isomorphism. If
$R=\mathbb{Z}$
, this is trivial. If
$R$
is a quadratic order, this is the elliptic curve case of the isomorphism given in [Reference KaniKan11, Proposition 17, (48)]. If
$R$
is a maximal quaternionic order, then by Theorem 3.3(a) all f.p. torsion-free left
$R$
-modules are projective, i.e., direct summands of f.p. free left
$R$
-modules; since
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is fully faithful when restricted to free modules, it is also fully faithful on projective modules.
(b) Let
$M$
be a f.p. torsion-free left
$R$
-module. Then
$$\begin{eqnarray}\operatorname{Hom}(\mathscr{H}\!\mathit{om}_{R}(M,E),E)=\operatorname{Hom}(\mathscr{H}\!\mathit{om}_{R}(M,E),\mathscr{H}\!\mathit{om}_{R}(R,E))=\operatorname{Hom}_{R}(R,M)=M\end{eqnarray}$$
since
$E=\mathscr{H}\!\mathit{om}_{R}(R,E)$
and
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is fully faithful by (a).
(c) As remarked in the proof of (a), every f.p. torsion-free left
$R$
-module is a finite direct sum of nonzero left
$R$
-ideals
$I$
.◻
5 Maximal abelian varieties over
$\mathbb{F}_{p^{2}}$
Fix a prime
$p$
. Call an abelian variety
$A$
over
$\mathbb{F}_{p^{2}}$
maximal if
$A$
has the maximum possible number of
$\mathbb{F}_{p^{2}}$
-points for its dimension, namely
$(p+1)^{2\dim A}$
.
Proposition 5.1. Let
$A$
be a
$g$
-dimensional abelian variety over
$\mathbb{F}_{p^{2}}$
. Let
$\ell$
be a prime not equal to
$p$
. The following are equivalent:
(a) The abelian variety
$A$
is maximal; i.e.,
$\#A(\mathbb{F}_{p^{2}})=(p+1)^{2g}$
.(b) The characteristic polynomial of
$\unicode[STIX]{x1D70B}_{A}$
on
$T_{\ell }A$
equals
$(x+p)^{2g}$
.(c) We have
$\unicode[STIX]{x1D70B}_{A}=-p$
.(d) We have
$A(\mathbb{F}_{p^{2}})\simeq (\mathbb{Z}/(p+1)\mathbb{Z})^{2g}$
as abelian groups.If
$E$
is a fixed maximal elliptic curve over
$\mathbb{F}_{p^{2}}$
, then the following also is equivalent to the above:(e) The abelian variety
$A$
is isogenous to
$E^{g}$
.
Proof. (a)
$\Rightarrow$
(b) Let
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{2g}\in \overline{\mathbb{Q}}$
be the eigenvalues of
$\unicode[STIX]{x1D70B}_{A}$
acting on
$T_{\ell }A$
. Then
$|\unicode[STIX]{x1D706}_{i}|=p$
and
$\#A(\mathbb{F}_{p^{2}})=\prod (1-\unicode[STIX]{x1D706}_{i})=\prod |1-\unicode[STIX]{x1D706}_{i}|\leqslant (p+1)^{2g}$
; if equality holds, then
$\unicode[STIX]{x1D706}_{i}=-p$
for all
$i$
. Thus the characteristic polynomial is
$(x+p)^{2g}$
.
(b)
$\Rightarrow$
(c) Since
$\unicode[STIX]{x1D70B}_{A}$
is determined by its action on
$T_{\ell }A$
, which is semisimple [Reference MumfordMum70, pp. 203–206], we obtain
$\unicode[STIX]{x1D70B}_{A}=-p$
.
(c)
$\Rightarrow$
(d) We have
$$\begin{eqnarray}A(\mathbb{F}_{p^{2}})=\ker (\unicode[STIX]{x1D70B}_{A}-1)(\overline{\mathbb{F}}_{p})=\ker (-p-1)(\overline{\mathbb{F}}_{p})=A[p+1](\overline{\mathbb{F}}_{p})\simeq (\mathbb{Z}/(p+1)\mathbb{Z})^{2g}.\end{eqnarray}$$
(d)
$\Rightarrow$
(a) Trivial.
(e)
$\Leftrightarrow$
(b) By (a)
$\Rightarrow$
(b), the characteristic polynomial of
$\unicode[STIX]{x1D70B}_{E}$
is
$(x+p)^{2}$
, so the characteristic polynomial of
$\unicode[STIX]{x1D70B}_{E^{g}}$
is
$(x+p)^{2g}$
. Two abelian varieties over a finite field are isogenous if and only if their characteristic polynomials are equal [Reference TateTat66, Theorem 1(c)].◻
Lemma 5.2. If
$A$
and
$B$
are maximal abelian varieties over
$\mathbb{F}_{p^{2}}$
, then any homomorphism
$A_{\overline{\mathbb{F}}_{p}}\rightarrow B_{\overline{\mathbb{F}}_{p}}$
is the base extension of a homomorphism
$A\rightarrow B$
.
Proof. Any homomorphism respects the
$p^{2}$
-power Frobenius endomorphisms (both are equal to
$-p$
) and hence descends to
$\mathbb{F}_{p^{2}}$
.◻
Every supersingular elliptic curve over
$\overline{\mathbb{F}}_{p}$
admits a unique model over
$\mathbb{F}_{p^{2}}$
that is maximal: the existence is [Reference Baker, González-Jiménez, González and PoonenBGGP05, Lemma 3.21], and uniqueness follows from Lemma 5.2. In particular, maximal elliptic curves over
$\mathbb{F}_{p^{2}}$
exist. If
$E$
is any such curve, then
$E$
is supersingular, and Lemma 5.2 implies that
$\operatorname{End}E=\operatorname{End}E_{\overline{\mathbb{F}}_{p}}$
, which is a maximal order
${\mathcal{O}}$
in a quaternion algebra over
$\mathbb{Q}$
ramified at
$p$
and
$\infty$
. Also, the kernel of the
$p$
-power Frobenius morphism
$E\rightarrow E^{(p)}$
is isomorphic to
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
.
By Proposition 5.1(a)
$\Rightarrow$
(e), any maximal abelian variety
$A$
over
$\mathbb{F}_{p^{2}}$
is isogenous to a power of
$E$
. The main result of this section strengthens this as follows.
Theorem 5.3.
(a) Every maximal abelian variety
$A$
over
$\mathbb{F}_{p^{2}}$
is isomorphic to a product of maximal elliptic curves over
$\mathbb{F}_{p^{2}}$
.(b) Fix a maximal elliptic curve
$E$
over
$\mathbb{F}_{p^{2}}$
. Let
${\mathcal{O}}:=\operatorname{End}E$
. Then the functors
$\mathscr{H}\!\mathit{om}_{{\mathcal{O}}}(-,E)$
and
$\operatorname{Hom}(-,E)$
are inverse equivalences of categories. Also, the categories involved can be rewritten so that
$\mathscr{H}\!\mathit{om}_{{\mathcal{O}}}(-,E)$
becomes $$\begin{eqnarray}\mathscr{H}\!\mathit{om}_{{\mathcal{O}}}(-,E):\{\text{f.p. projective left }{\mathcal{O}}\text{-modules}\}^{\operatorname{opp}}\stackrel{{\sim}}{\longrightarrow }\{\text{maximal abelian varieties}/\mathbb{F}_{p^{2}}\}.\end{eqnarray}$$
(c) Fix a maximal elliptic curve
$E$
over
$\mathbb{F}_{p^{2}}$
. Let
$g\geqslant 2$
. Every
$g$
-dimensional maximal abelian variety over
$\mathbb{F}_{p^{2}}$
is isomorphic to
$E^{g}$
. In particular, any product of
$g$
maximal elliptic curves over
$\mathbb{F}_{p^{2}}$
is isomorphic to any other.
The analogous results hold if maximal is replaced by minimal; i.e., we consider abelian varieties
$A$
over
$\mathbb{F}_{p^{2}}$
such that
$\#A(\mathbb{F}_{p^{2}})=(p-1)^{2\dim A}$
.
We need a few lemmas for the proof of Theorem 5.3.
Lemma 5.4. There exists an elliptic curve
$E$
over
$\mathbb{F}_{p}$
such that
$E_{\mathbb{F}_{p^{2}}}$
is maximal.
Proof. There exists an elliptic curve
$E$
over
$\mathbb{F}_{p}$
with
$p+1$
points [Reference WaterhouseWat69, Theorem 4.1(5)(i)]. The
$p$
-power Frobenius endomorphism
$\unicode[STIX]{x1D70B}_{E}$
of
$E$
satisfies
$\unicode[STIX]{x1D70B}_{E}^{2}=-p$
, so
$E_{\mathbb{F}_{p^{2}}}$
satisfies condition (c) in Proposition 5.1.◻
Lemma 5.5. If
$E$
and
$E^{\prime }$
are maximal elliptic curves over
$\mathbb{F}_{p^{2}}$
, there exists a separable isogeny
$E\rightarrow E^{\prime }$
.
Proof. For elliptic curves
$E$
and
$E^{\prime }$
, write
$E\sim E^{\prime }$
if there exists an isogeny
$E\rightarrow E^{\prime }$
of degree prime to
$p$
. The relation
${\sim}$
is an equivalence relation: reflexive because of the identity, symmetric because of the dual isogeny (which has the same degree), and transitive because of composition of isogenies.
Any isogeny
$\unicode[STIX]{x1D719}:E\rightarrow E^{\prime }$
factors as
$f\circ \unicode[STIX]{x1D706}$
where
$\deg f=p^{n}$
for some
$n\geqslant 1$
, and
$p\nmid \deg \unicode[STIX]{x1D706}$
. Here
$\unicode[STIX]{x1D706}$
is separable. On the other hand,
$f$
is a factor of
$[p^{n}]$
, which is purely inseparable if
$E$
is maximal. Thus, assuming that
$E$
is maximal,
$\unicode[STIX]{x1D719}$
is separable if and only if
$p\nmid \deg \unicode[STIX]{x1D719}$
.
Let
$E_{0}$
be the maximal elliptic curve over
$\mathbb{F}_{p^{2}}$
in Lemma 5.4. Since
$\#E_{0}(\mathbb{F}_{p^{2}})=\#E(\mathbb{F}_{p^{2}})$
, there exists an isogeny
$E_{0}\rightarrow E$
, which factors as
$E_{0}\stackrel{f}{\rightarrow }E_{0}\stackrel{\unicode[STIX]{x1D706}}{\rightarrow }E$
, where
$f$
is a power of the
$p$
-power Frobenius morphism (which goes from
$E_{0}$
to itself since
$E_{0}$
is definable over
$\mathbb{F}_{p}$
), and
$\unicode[STIX]{x1D706}$
is separable. By the previous paragraph,
$p\nmid \deg \unicode[STIX]{x1D706}$
. Thus
$E_{0}\sim E$
. Similarly,
$E_{0}\sim E^{\prime }$
, so
$E\sim E^{\prime }$
. Thus there exists an isogeny
$E\rightarrow E^{\prime }$
of degree prime to
$p$
. Any such isogeny is separable.◻
Remark 5.6. Even better, if
$E$
and
$E^{\prime }$
are maximal elliptic curves over
$\mathbb{F}_{p^{2}}$
, there exists an isogeny of
$\ell$
-power degree for any prime
$\ell \neq p$
: for an argument due to Serre, see [Reference MestreMes86, p. 223].
Lemma 5.7. If
$A$
is a maximal abelian variety over
$\mathbb{F}_{p^{2}}$
, then every finite étale subgroup scheme of
$A_{\overline{\mathbb{F}}_{p}}$
is defined over
$\mathbb{F}_{p^{2}}$
.
Proof. The
$p^{2}$
-power Frobenius field automorphism acts on (prime-to-
$p$
) torsion points of
$A_{\overline{\mathbb{F}}_{p}}$
as
$-p$
, so it preserves any finite subgroup of order prime to
$p$
.◻
Corollary 5.8. If
$A$
is a maximal abelian variety over
$\mathbb{F}_{p^{2}}$
, and
$G$
is a nonzero finite étale subgroup scheme of
$A$
, then
$G$
contains a subgroup scheme of prime order.
Proof. Choose a prime-order subgroup of
$G(\overline{\mathbb{F}}_{p})$
. The corresponding finite étale subgroup scheme of
$G_{\overline{\mathbb{F}}_{p}}$
is defined over
$\mathbb{F}_{p^{2}}$
by Lemma 5.7.◻
Lemma 5.9. Let
$A$
be a supersingular abelian variety over a field
$k$
of characteristic
$p$
. Every
$p$
-power order subgroup scheme
$G\subseteq A$
is an iterated extension of copies of
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
.
Proof. By induction, it suffices to show that, if
$G\neq 0$
, then
$G$
contains a copy of
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
. The
$a$
-number
$\dim _{k}\operatorname{Hom}(\boldsymbol{\unicode[STIX]{x1D6FC}}_{p},G)$
is unchanged by field extension [Reference Li and OortLO98, §1.5], so we may assume that
$k$
is algebraically closed. Then
$A$
is isogenous to a power
$E^{r}$
of a supersingular elliptic curve. The group scheme
$E[p]$
is an extension of
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
by
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
, so all Jordan–Hölder factors of
$E[p^{n}]$
are isomorphic to
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
. The image of
$E[p^{N}]$
under the isogeny
$E^{r}\rightarrow A$
contains
$A[p^{n}]$
if
$N$
is sufficiently large relative to
$n$
, and
$A[p^{n}]$
contains
$G$
if
$n$
is large enough. Thus all Jordan–Hölder factors of
$G$
are isomorphic to
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
.◻
Lemma 5.10. Let
$E$
and
$E^{\prime }$
be maximal elliptic curves over
$\mathbb{F}_{p^{2}}$
. Identify
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
with a subgroup scheme of each. Then each homomorphism
$E\rightarrow E^{\prime }$
restricts to a homomorphism
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}\rightarrow \boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
and the resulting map
$$\begin{eqnarray}\operatorname{Hom}(E,E^{\prime })\longrightarrow \operatorname{End}\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}\simeq \mathbb{F}_{p^{2}}\end{eqnarray}$$
is surjective.
Proof. Since each
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
is the kernel of the
$p$
-power Frobenius morphism, any homomorphism
$E\rightarrow E^{\prime }$
must map
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
to
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
. If
$E^{\prime }=E$
, then the resulting ring homomorphism
$$\begin{eqnarray}\operatorname{End}E\longrightarrow \operatorname{End}\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}\simeq \mathbb{F}_{p^{2}}\end{eqnarray}$$
is surjective because every ring homomorphism from
${\mathcal{O}}$
to
$\mathbb{F}_{p^{2}}$
is surjective. In the general case, Lemma 5.5 provides a separable isogeny
$\unicode[STIX]{x1D706}:E\rightarrow E^{\prime }$
; then
$\unicode[STIX]{x1D706}|_{\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}}\neq 0$
, so
$\{\unicode[STIX]{x1D706}\circ e:e\in \operatorname{End}E\}$
surjects onto
$\operatorname{End}\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
.◻
Lemma 5.11. Let
$E$
and
$E^{\prime }$
be maximal elliptic curves over
$\mathbb{F}_{p^{2}}$
. Let
$G$
be a subgroup scheme of
$E$
such that
$\#G$
is prime. Then every homomorphism
$h:G\rightarrow E^{\prime }$
extends to a homomorphism
$E\rightarrow E^{\prime }$
.
Proof.
Case 1:
$\#G$
is a prime
$\ell \neq p$
. Then extend
$G(\overline{\mathbb{F}}_{p})\rightarrow E^{\prime }(\overline{\mathbb{F}}_{p})$
to a homomorphism
$E[\ell ](\overline{\mathbb{F}}_{p})\rightarrow E^{\prime }[\ell ](\overline{\mathbb{F}}_{p})$
and lift it arbitrarily to a
$\mathbb{Z}_{\ell }$
-module homomorphism
$t:T_{\ell }E\rightarrow T_{\ell }E^{\prime }$
. Since the
$p^{2}$
-power Frobenius automorphism acts as
$-p$
on both sides,
$t$
respects the action of
${\mathcal{G}}_{\mathbb{F}_{p^{2}}}$
. By Tate’s theorem on homomorphisms [Reference TateTat66],
$t$
comes from some
$\unicode[STIX]{x1D70F}\in \operatorname{Hom}(E,E^{\prime })\otimes \mathbb{Z}_{\ell }$
. Any
$\unicode[STIX]{x1D70F}^{\prime }\in \operatorname{Hom}(E,E^{\prime })$
congruent to
$\unicode[STIX]{x1D70F}$
modulo
$\ell$
extends
$h$
.
Case 2:
$\#G=p$
. By Lemma 5.9,
$G$
is the copy of
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
of
$E$
(the kernel of the
$p$
-power Frobenius morphism). By Lemma 5.10,
$h$
extends to a homomorphism
$E\rightarrow E^{\prime }$
.◻
Lemma 5.12. Let
$f:X\rightarrow Y$
be a homomorphism of commutative group schemes. Let
$\unicode[STIX]{x1D6E4}$
be the graph of
$f$
. Then there exists an automorphism of
$X\times Y$
sending
$\unicode[STIX]{x1D6E4}$
to
$X\times \{0\}$
.
Proof. Use
$(x,y)\mapsto (x,y-f(x))$
, which has inverse
$(x,y)\mapsto (x,y+f(x))$
.◻
Lemma 5.13. Let
$B$
be a product
$E_{1}\times \cdots \times E_{g}$
of maximal elliptic curves over
$\mathbb{F}_{p^{2}}$
. Let
$G$
be a finite subgroup scheme of
$B$
. Then
$B/G$
is isomorphic to a product of maximal elliptic curves over
$\mathbb{F}_{p^{2}}$
.
Proof. First suppose that
$\#G$
is prime. Let
$\operatorname{pr}_{j}:B\rightarrow E_{j}$
denote the
$j$
th projection. Then
$\operatorname{pr}_{j}(G)\neq 0$
for some
$j$
, say
$j=1$
. Since
$\#G$
is prime,
$\operatorname{pr}_{1}$
maps
$G$
isomorphically to its image
$G_{1}\subset E_{1}$
. Thus
$G$
is the graph of a homomorphism
$h:G_{1}\rightarrow E_{2}\times \cdots \times E_{g}$
. Applying Lemma 5.11 to each factor
$G_{1}\rightarrow E_{j}$
shows that
$h$
extends to a homomorphism
$f:E_{1}\rightarrow \prod _{j\geqslant 2}E_{j}$
. Then
$G$
is contained in the graph of
$f$
. By Lemma 5.12, after applying an automorphism of
$B$
we may assume that
$G\subseteq E_{1}$
. Then
$B/G$
is the product of the maximal elliptic curves
$E_{1}/G,E_{2},\ldots ,E_{g}$
.
By Corollary 5.8 and Lemma 5.9, every Jordan–Hölder factor of
$G$
has prime order, so the general case follows by induction.◻
Proof of Theorem 5.3.
(a) By Proposition 5.1(a)
$\Rightarrow$
(e),
$A\simeq B/G$
, where
$B$
is a product of maximal elliptic curves (in fact, a power) and
$G$
is a finite subgroup scheme of
$B$
. Apply Lemma 5.13.
(b) First let us justify the rewriting of the categories. F.p. torsion-free left
${\mathcal{O}}$
-modules are projective by Theorem 3.3(a). By Proposition 5.1(a)
$\Leftrightarrow$
(e), the abelian varieties isogenous to a power of
$E$
are exactly the maximal abelian varieties over
$\mathbb{F}_{p^{2}}$
.
By (a), every maximal abelian variety is a product of maximal elliptic curves, each of which is
$\mathscr{H}\!\mathit{om}_{{\mathcal{O}}}(I,E)$
for some left
${\mathcal{O}}$
-ideal
$I$
, by the bottom of page 541 in [Reference WaterhouseWat69]. The result now follows from Theorem 4.8.
(c) Combine Theorem 3.3(c) and part (b).
The same proofs apply in the minimal case. ◻
Remark 5.14. Because of Lemma 5.2, Theorem 5.3(c) could be deduced also from its analogue over
$\overline{\mathbb{F}}_{p}$
, that for
$g\geqslant 2$
, any product of
$g$
supersingular elliptic curves over
$\overline{\mathbb{F}}_{p}$
is isomorphic to any other. The latter is a well-known theorem of Deligne, proved in a similar way: see [Reference OgusOgu79, Theorem 6.2] and [Reference Shioda and LønstedShi79, Theorem 3.5].
Remark 5.15. A related result can be found in [Reference OortOor75]: Theorem 2 there states that, if
$A$
is an abelian variety over an algebraically closed field of characteristic
$p$
, and the
$a$
-number of
$A$
equals
$\dim A$
, then
$A$
is isomorphic to a product of supersingular elliptic curves.
6 Kernel subgroups
6.1 General properties of kernel subgroups
Definition 6.1. Let
$A$
be an abelian variety over a field. Call a subgroup scheme
$G\subseteq A$
a kernel subgroup if
$G=A[I]$
for some
$I\subseteq \operatorname{End}A$
. (These are called ideal subgroups in [Reference KaniKan11, p. 302].)
In the definition, we may replace
$I$
by the left
$(\operatorname{End}A)$
-ideal it generates without changing
$A[I]$
. Thus we may always assume that
$I$
is a left
$(\operatorname{End}A)$
-ideal.
Proposition 6.2.
(a) An intersection of kernel subgroups in
$A$
is a kernel subgroup.(b) Let
$A_{1},\ldots ,A_{n}$
be abelian varieties. Suppose that
$G_{i}\subseteq A_{i}$
for
$i=1,\ldots ,n$
. Then
$\prod _{i=1}^{n}G_{i}$
is a kernel subgroup of
$\prod _{i=1}^{n}A_{i}$
if and only if each
$G_{i}$
is a kernel subgroup of
$A_{i}$
.(c) Let
$I_{1},\ldots ,I_{n}$
be pairwise coprime
$2$
-sided ideals of
$\operatorname{End}A$
. Let
$G_{i}\subseteq A[I_{i}]$
for
$i=1,\ldots ,n$
. Then
$\sum _{i=1}^{n}G_{i}$
is a kernel subgroup if and only if each
$G_{i}$
is a kernel subgroup.
Proof. (a) We have
$\bigcap A[I_{i}]=A[\sum I_{i}]$
for any left ideals
$I_{i}$
.
(b) Let
$A=\prod A_{i}$
and
$G=\prod G_{i}$
. Suppose that
$G=A[I]$
. For each
$f\in I$
, the composition
$A_{i}{\hookrightarrow}A\stackrel{f}{\rightarrow }A{\twoheadrightarrow}A_{i}$
defines
$\bar{f}\in \operatorname{End}A_{i}$
, and
$G_{i}$
is the intersection of the kernels of all such
$\bar{f}$
.
Conversely, suppose that
$G_{i}=A_{i}[I_{i}]$
for each
$i$
. Let
$I:=\prod I_{i}$
denote the set of ‘diagonal’ endomorphisms
$(f_{1},\ldots ,f_{n}):A\rightarrow A$
with
$f_{i}\in I_{i}$
. Then
$G=A[I]$
.
(c) By induction, we may assume
$n=2$
. Since
$I_{1}$
and
$I_{2}$
are coprime
$2$
-sided ideals, we have
$A[I_{1}I_{2}]=A[I_{1}]\oplus A[I_{2}]$
, and every subgroup scheme
$H\subseteq A[I_{1}I_{2}]$
decomposes as
$H_{1}\oplus H_{2}$
, where
$H_{i}\subseteq A[I_{i}]$
; namely,
$H_{i}=H\cap A[I_{i}]$
.
If
$G_{1}+G_{2}$
is a kernel subgroup, then so is
$G_{i}=(G_{1}+G_{2})\cap A[I_{i}]$
, by (a).
Conversely, suppose that
$G_{i}=A[J_{i}]$
for some left ideal
$J_{i}$
. Replace
$J_{i}$
by
$J_{i}+I_{i}$
to assume that
$J_{i}\supseteq I_{i}$
. Let
$K:=I_{2}J_{1}+I_{1}J_{2}$
. We claim that
$A[K]=G_{1}+G_{2}$
. First,
$I_{2}J_{1}\subseteq J_{1}$
, which kills
$G_{1}$
; also,
$I_{1}J_{2}\subseteq I_{1}$
, which kills
$G_{1}$
. Thus
$K$
kills
$G_{1}$
. Similarly,
$K$
kills
$G_{2}$
. Thus
$G_{1}+G_{2}\subseteq A[K]$
. On the other hand, if we write
$A[K]=H_{1}\oplus H_{2}$
with
$H_{i}\subseteq A[I_{i}]$
, we will show that
$H_{i}\subseteq G_{i}$
, so that
$A[K]\subseteq G_{1}+G_{2}$
. Write
$1=e_{1}+e_{2}$
with
$e_{i}\in I_{i}$
. Then the subsets
$e_{1}J_{1}\subseteq I_{2}J_{1}\subseteq K$
and
$e_{2}J_{1}\subseteq I_{2}$
kill
$H_{1}$
, so
$J_{1}$
kills
$H_{1}$
; i.e.,
$H_{1}\subseteq A[J_{1}]=G_{1}$
. Similarly
$H_{2}\subseteq G_{2}$
. So
$A[K]\subseteq G_{1}+G_{2}$
. Hence
$G_{1}+G_{2}=A[K]$
, a kernel subgroup.◻
6.2 Kernel subgroups of a power of an elliptic curve
Proposition 6.3. Let
$E$
be an elliptic curve over a field, and let
$r\in \mathbb{Z}_{{\geqslant}0}$
. Let
$R:=\operatorname{End}E$
. For a subgroup scheme
$G\subseteq E^{r}$
, the following are equivalent:
(i)
$G$
is a kernel subgroup.(ii)
$G$
is the kernel of a homomorphism
$E^{r}\rightarrow E^{s}$
for some
$s\in \mathbb{Z}_{{\geqslant}0}$
.(iii) There exists a f.p. torsion-free
$R$
-module
$M$
such that
$E^{r}/G\simeq \mathscr{H}\!\mathit{om}_{R}(M,E)$
.(iv) There exists a submodule
$M\subseteq R^{r}$
such that applying
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
to yields$$\begin{eqnarray}0\rightarrow M\rightarrow R^{r}\rightarrow R^{r}/M\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow G\rightarrow E^{r}\rightarrow E^{r}/G\rightarrow 0.\end{eqnarray}$$
Proof. (i)
$\Rightarrow$
(ii) Suppose that
$G$
is a kernel subgroup, say
$A[I]$
. Let
$f_{1},\ldots ,f_{n}$
be generators for
$I$
. Then
$G$
is the kernel of 
(ii)
$\Rightarrow$
(iii) This is a special case of Theorem 4.4(c).
(iii)
$\Rightarrow$
(iv) If
$E^{r}/G\simeq \mathscr{H}\!\mathit{om}_{R}(M,E)$
for some f.p. torsion-free
$M$
, then by Theorem 4.8(a), the natural surjection
$E^{r}{\twoheadrightarrow}E^{r}/G$
comes from some injection
$M{\hookrightarrow}R^{r}$
. Applying
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
to
$$\begin{eqnarray}0\rightarrow M\rightarrow R^{r}\rightarrow R^{r}/M\rightarrow 0\end{eqnarray}$$
yields
$$\begin{eqnarray}0\rightarrow H\rightarrow E^{r}{\twoheadrightarrow}E^{r}/G\end{eqnarray}$$
for some
$H$
, which must be isomorphic to
$G$
.
(iv)
$\Rightarrow$
(ii) Choose a surjection
$h:R^{s}{\twoheadrightarrow}M$
. Applying
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
to the composition
$R^{s}\stackrel{h}{{\twoheadrightarrow}}M{\hookrightarrow}R^{r}$
produces a homomorphism
$E^{r}{\twoheadrightarrow}E^{r}/G{\hookrightarrow}E^{s}$
with kernel
$G$
.
(ii)
$\Rightarrow$
(i) We may increase
$s$
to assume that
$r|s$
. Then
$G$
is an intersection of
$s/r$
endomorphisms of
$E^{r}$
, so it is a kernel subgroup by Proposition 6.2(a).◻
Proposition 6.4. Let
$E$
be an elliptic curve. Let
$R:=\operatorname{End}E$
. Then the following are equivalent:
(i) For each
$r\in \mathbb{Z}_{{\geqslant}0}$
, every subgroup scheme of
$E^{r}$
is a kernel subgroup.(ii) For each
$r\in \mathbb{Z}_{{\geqslant}0}$
, every finite subgroup scheme of
$E^{r}$
is a kernel subgroup.(iii) The functors
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are inverse equivalences of categories.
Proof. (i)
$\Rightarrow$
(ii) Trivial.
(ii)
$\Rightarrow$
(iii) Suppose that
$A$
is an abelian variety isogenous to
$E^{r}$
. Then
$A\simeq E^{r}/G$
for some finite subgroup scheme
$G$
. By assumption,
$G$
is a kernel subgroup. Proposition 6.3(i)
$\Rightarrow$
(iii) implies that
$A$
is in the image of
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
. The result now follows from Theorem 4.8.
(iii)
$\Rightarrow$
(i) Let
$G$
be a subgroup scheme of
$E^{r}$
. Then
$E^{r}/G$
is isogenous to
$E^{s}$
for some
$s\leqslant r$
. By assumption,
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is an equivalence of categories, so
$E^{r}/G$
is of the form
$\mathscr{H}\!\mathit{om}_{R}(M,E)$
. By Proposition 6.3(iii)
$\Rightarrow$
(i),
$G$
is a kernel subgroup.◻
In the next few sections, we investigate when it holds that all finite subgroup schemes of powers of
$E$
are kernel subgroups, in order to determine when
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are inverse equivalences of categories.
6.3 Prime-to-
$p$
subgroups
We continue to assume that
$E$
is an elliptic curve and
$R=\operatorname{End}E$
. Let
$\ell$
be a prime not equal to
$\operatorname{char}k$
. Let
$R_{\ell }:=R\otimes \mathbb{Z}_{\ell }$
. The natural map
$R_{\ell }\rightarrow \operatorname{End}_{\mathbb{Z}_{\ell }}T_{\ell }E$
is injective since an endomorphism that kills
$E[\ell ^{n}]$
for all
$n$
is
$0$
, and has saturated image since an endomorphism that kills
$E[\ell ]$
is equal to
$\ell$
times an endomorphism. Let
$C:=\operatorname{End}_{R_{\ell }}T_{\ell }E$
, which is the commutant of
$R_{\ell }$
in
$\operatorname{End}_{\mathbb{Z}_{\ell }}T_{\ell }E\simeq \operatorname{M}_{2}(\mathbb{Z}_{\ell })$
. For any elliptic curve, we have
$\operatorname{rk}R\in \{1,2,4\}$
, so one of the following holds:
(i)
$R_{\ell }=\mathbb{Z}_{\ell }$
and
$C=\operatorname{M}_{2}(\mathbb{Z}_{\ell })$
;(ii)
$R_{\ell }=C=\mathbb{Z}_{\ell }\oplus \mathbb{Z}_{\ell }\unicode[STIX]{x1D6FC}$
, a
$\mathbb{Z}_{\ell }$
-algebra that is a saturated rank
$2$
$\mathbb{Z}_{\ell }$
-submodule of
$\operatorname{M}_{2}(\mathbb{Z}_{\ell })$
for some
$\unicode[STIX]{x1D6FC}\in \operatorname{M}_{2}(\mathbb{Z}_{\ell })$
; or(iii)
$R_{\ell }=\operatorname{M}_{2}(\mathbb{Z}_{\ell })$
and
$C=\mathbb{Z}_{\ell }$
.
(To see that
$C=R_{\ell }$
in case (ii), one may argue as follows. By [Reference MumfordMum70, III, §19, Corollary 3], the
$\mathbb{Q}$
-algebra
$R\otimes \mathbb{Q}$
is semisimple, so
$R\otimes \mathbb{Q}_{\ell }$
is either a degree
$2$
field extension of
$\mathbb{Q}_{\ell }$
, or is conjugate to
$\mathbb{Q}_{\ell }\times \mathbb{Q}_{\ell }$
. In either case, the commutant
$C\otimes _{\mathbb{Z}_{\ell }}\mathbb{Q}_{\ell }$
of
$R\otimes \mathbb{Q}_{\ell }$
in
$\operatorname{M}_{2}(\mathbb{Q}_{\ell })$
is 2-dimensional. On the other hand, an algebra generated by one element is commutative, so
$C$
contains
$R_{\ell }$
. Also,
$R_{\ell }$
is saturated in
$\operatorname{M}_{2}(\mathbb{Z}_{\ell })$
. The previous three sentences imply that
$C=R_{\ell }$
.)
Let
$e\in \mathbb{Z}_{{>}0}$
.
Lemma 6.5. Every finitely generated left
$C/\ell ^{e}C$
-module injects into a free
$C/\ell ^{e}C$
-module.
Proof. If
$C=\mathbb{Z}_{\ell }$
, this is trivial. For any ring
$A$
and positive integer
$n$
, the category of
$A$
-modules is equivalent to the category of
$\operatorname{M}_{n}(A)$
-modules [Reference LamLam99, Theorem 17.20], and the equivalence preserves injections, finite generation, and projectivity [Reference LamLam99, Remark 17.23(A)]; applying this to
$A=\mathbb{Z}_{\ell }/\ell ^{e}\mathbb{Z}_{\ell }$
and
$n=2$
shows that the case
$C=\mathbb{Z}_{\ell }$
implies the case
$C=\operatorname{M}_{2}(\mathbb{Z}_{\ell })$
.
Finally, suppose that
$C$
is of rank
$2$
. Then
$C/\ell ^{e}C$
is free of rank
$2$
over
$\mathbb{Z}/\ell ^{e}\mathbb{Z}$
; say, with basis
$1$
,
$\unicode[STIX]{x1D6FC}$
. For
$c\in C/\ell ^{e}C$
, let
$\unicode[STIX]{x1D706}(c)$
be the coefficient of
$\unicode[STIX]{x1D6FC}$
in
$c$
. Multiplying any nonzero element of
$\ker \unicode[STIX]{x1D706}$
by
$\unicode[STIX]{x1D6FC}$
gives an element outside
$\ker \unicode[STIX]{x1D706}$
. Therefore the pairing
$$\begin{eqnarray}\displaystyle C/\ell ^{e}C\times C/\ell ^{e}C & \longrightarrow & \displaystyle \mathbb{Z}/\ell ^{e}\mathbb{Z},\nonumber\\ \displaystyle x,y & \longmapsto & \displaystyle \unicode[STIX]{x1D706}(xy)\nonumber\end{eqnarray}$$
is a perfect pairing. In other words, the Pontryagin dual
$(C/\ell ^{e}C)^{D}$
is isomorphic to
$C/\ell ^{e}C$
as a
$C/\ell ^{e}C$
-module. If
$M$
is a finitely generated
$C/\ell ^{e}C$
-module, there exists a surjection
$(C/\ell ^{e}C)^{r}{\twoheadrightarrow}M^{D}$
for some
$r\in \mathbb{Z}_{{\geqslant}0}$
; taking Pontryagin duals yields an injection
$$\begin{eqnarray}M{\hookrightarrow}((C/\ell ^{e}C)^{r})^{D}\simeq (C/\ell ^{e}C)^{r}.\end{eqnarray}$$
◻
Lemma 6.6. The group
$(T_{\ell }E)^{2}$
is free as an
$R_{\ell }$
-module and as a
$C$
-module. The group
$E[\ell ^{e}](k_{s})^{2}$
is free as an
$R/\ell ^{e}R$
-module and as a
$C/\ell ^{e}C$
-module.
Proof. Since
$E[\ell ^{e}](k_{s})=T_{\ell }E/\ell ^{e}T_{\ell }E$
, by Nakayama’s lemma it is enough to check that
$E[\ell ](k_{s})^{2}$
is free as an
$A$
-module, for
$A=R/\ell R$
and for
$A=C/\ell C$
. Identify
$E[\ell ](k_{s})^{2}$
with
$\mathbb{F}_{\ell }^{2}$
, so that
$A\subseteq \operatorname{M}_{2}(\mathbb{F}_{\ell })$
. The case
$A=\mathbb{F}_{\ell }$
is trivial. If
$A$
is
$\mathbb{F}_{\ell }\oplus \mathbb{F}_{\ell }\unicode[STIX]{x1D6FC}$
for some
$\unicode[STIX]{x1D6FC}\in \operatorname{M}_{2}(\mathbb{F}_{\ell })$
, then every faithful
$A$
-module of dimension
$2$
over
$\mathbb{F}_{\ell }$
is free. If
$A=\operatorname{M}_{2}(\mathbb{F}_{\ell })$
, then the free
$A$
-module
$A$
is a direct sum of two copies of
$\mathbb{F}_{\ell }^{2}$
(the two column spaces).◻
Lemma 6.7. The natural maps
$$\begin{eqnarray}\displaystyle C/\ell ^{e}C & \longrightarrow & \displaystyle \operatorname{End}_{R/\ell ^{e}R}E[\ell ^{e}](k_{s}),\nonumber\\ \displaystyle R/\ell ^{e}R & \longrightarrow & \displaystyle \operatorname{End}_{C/\ell ^{e}C}E[\ell ^{e}](k_{s})\nonumber\end{eqnarray}$$
are isomorphisms.
Proof. The first map is an isomorphism since
$C=\operatorname{End}_{R_{\ell }}T_{\ell }E$
and
$C$
and
$R_{\ell }$
are saturated in
$\operatorname{End}T_{\ell }E\simeq \operatorname{M}_{2}(\mathbb{Z}_{\ell })$
. Lemma 6.6 and [Reference LamLam99, Theorem 18.8(3)
$\Rightarrow$
(1)] imply that
$E[\ell ^{e}](k_{s})$
is a generator of the category of finitely generated
$R/\ell ^{e}R$
-modules, so [Reference LamLam99, Proposition 18.17(2)(d)] yields the second isomorphism.◻
Recall that
${\mathcal{G}}_{k}=\operatorname{Gal}(k_{s}/k)$
. There is a group homomorphism
${\mathcal{G}}_{k}\rightarrow C^{\times }$
since each
$\unicode[STIX]{x1D70E}\in {\mathcal{G}}_{k}$
respects the
$R$
-action on the groups
$E[\ell ^{e}](k_{s})$
and
$T_{\ell }E$
.
Proposition 6.8. Let
$E$
be an elliptic curve over a field
$k$
. Let
$\ell$
,
$e$
, and
$C$
be as above. Let
$G$
be a subgroup scheme of
$E[\ell ^{e}]^{r}$
for some
$r$
. Then
$G$
is a kernel subgroup if and only if
$G(k_{s})$
is a
$C/\ell ^{e}C$
-submodule of
$E[\ell ^{e}]^{r}(k_{s})$
.
Proof. Suppose that
$G(k_{s})$
is a
$C/\ell ^{e}C$
-submodule of
$E[\ell ^{e}]^{r}(k_{s})$
. Let
$H:=E[\ell ^{e}]^{r}/G$
. Then
$H(k_{s})$
is a finitely generated
$C/\ell ^{e}C$
-module. By Lemma 6.5,
$H(k_{s})$
injects into a free
$C/\ell ^{e}C$
-module, which in turn injects into
$E[\ell ^{e}]^{s}(k_{s})$
for some
$s$
. Because of the homomorphisms
${\mathcal{G}}_{k}\rightarrow C^{\times }\rightarrow (C/\ell ^{e}C)^{\times }$
, the
$C/\ell ^{e}C$
-module homomorphism
$H(k_{s})\rightarrow E[\ell ^{e}]^{s}(k_{s})$
is a
${\mathcal{G}}_{k}$
-module homomorphism, so it comes from a homomorphism
$H\rightarrow E[\ell ^{e}]^{s}$
of étale group schemes. The composition
$E[\ell ^{e}]^{r}{\twoheadrightarrow}H{\hookrightarrow}E[\ell ^{e}]^{s}$
is given by an
$s\times r$
matrix
$N_{e}$
with entries in
$\operatorname{End}_{C/\ell ^{e}C}E[\ell ^{e}](k_{s})=R/\ell ^{e}R$
(the equality is Lemma 6.7). Lift
$N_{e}$
to
$N\in \operatorname{M}_{s\times r}(R)$
. Then
$G$
is the intersection of the kernel subgroups
$E[\ell ^{e}]^{r}$
and
$\ker (N:E^{r}\rightarrow E^{s})$
. By Propositions 6.2(a) and 6.3,
$G$
is a kernel subgroup.
Conversely, if
$G$
is a kernel subgroup, say the kernel of
$E^{r}\rightarrow E^{s}$
, then it is also the kernel of
$E[\ell ^{e}]^{r}\rightarrow E[\ell ^{e}]^{s}$
, which is a homomorphism of
$C/\ell ^{e}C$
-modules, so
$G$
is a
$C/\ell ^{e}C$
-module.◻
The group homomorphism
${\mathcal{G}}_{k}\rightarrow C^{\times }$
induces algebra homomorphisms
$\mathbb{Z}_{\ell }[{\mathcal{G}}_{k}]\rightarrow C$
and
$\mathbb{F}_{\ell }[{\mathcal{G}}_{k}]\rightarrow C/\ell C$
.
Proposition 6.9. Let
$E$
,
$k$
,
$\ell$
,
$R$
,
$R_{\ell }$
, and
$C$
be as above. The following are equivalent:
(i) The homomorphism
$\mathbb{F}_{\ell }[{\mathcal{G}}_{k}]\rightarrow C/\ell C$
is surjective.(ii) The homomorphism
$\mathbb{Z}_{\ell }[{\mathcal{G}}_{k}]\rightarrow C$
is surjective.(iii) Every
$\ell$
-power order subgroup scheme of
$E^{r}$
for every
$r$
is a kernel subgroup.
Proof. (i)
$\Rightarrow$
(ii) Nakayama’s lemma.
(ii)
$\Rightarrow$
(iii) Let
$G$
be an
$\ell$
-power subgroup scheme of
$E^{r}$
, say
$G\subseteq E[\ell ^{e}]^{r}$
. Then
$G(k_{s})$
is a
$\mathbb{Z}_{\ell }[{\mathcal{G}}_{k}]$
-module. Since
$\mathbb{Z}_{\ell }[{\mathcal{G}}_{k}]\rightarrow C$
is surjective,
$G(k_{s})$
is also a
$C$
-module, and hence a
$C/\ell ^{e}C$
-module. By Proposition 6.8,
$G$
is a kernel subgroup.
(iii)
$\Rightarrow$
(i) Suppose that
$\mathbb{F}_{\ell }[{\mathcal{G}}_{k}]\rightarrow C/\ell C$
is not surjective; let
$D$
be the image. The algebra
$C/\ell C$
is one of
$\mathbb{F}_{\ell }$
,
$\left\{\!\left(\begin{smallmatrix}a & b\\ 0 & a\end{smallmatrix}\right)\!\right\}\simeq \mathbb{F}_{\ell }[\unicode[STIX]{x1D716}]/(\unicode[STIX]{x1D716}^{2})$
,
$\left\{\!\left(\begin{smallmatrix}a & 0\\ 0 & b\end{smallmatrix}\right)\!\right\}\simeq \mathbb{F}_{\ell }\times \mathbb{F}_{\ell }$
,
$\mathbb{F}_{\ell ^{2}}$
, or
$\operatorname{M}_{2}(\mathbb{F}_{\ell })$
. The first is excluded since it has no nontrivial subalgebras. In the second, third, and fourth cases,
$D$
can only be
$\mathbb{F}_{\ell }$
, and it is easy to find a subspace of
$\mathbb{F}_{\ell }^{2}\simeq E[\ell ](k_{s})$
that is not a
$C/\ell C$
-module. In the fifth case,
$D$
is contained in a copy of either
$\left\{\!\left(\begin{smallmatrix}a & b\\ 0 & c\end{smallmatrix}\right)\!\right\}$
or
$\mathbb{F}_{\ell ^{2}}$
. Now
$\left\{\!\left(\begin{smallmatrix}a & b\\ 0 & c\end{smallmatrix}\right)\!\right\}$
fixes a line in
$\mathbb{F}_{\ell }^{2}$
not fixed by
$\operatorname{M}_{2}(\mathbb{F}_{\ell })$
. And
$\mathbb{F}_{\ell ^{2}}$
fixes an
$\mathbb{F}_{\ell ^{2}}$
-line in
$\mathbb{F}_{\ell ^{2}}^{2}\simeq E^{2}[\ell ](k_{s})$
that is not fixed by
$\operatorname{M}_{2}(\mathbb{F}_{\ell })$
. Thus in each case, there is a subgroup scheme of
$E[\ell ]$
or
$E^{2}[\ell ]$
that is not a
$C/\ell C$
-module, and hence by Proposition 6.8 not a kernel subgroup.◻
6.4
$p$
-power subgroups
Proposition 6.10. Let
$E$
be an ordinary elliptic curve over a field
$k$
of characteristic
$p$
. Assume that
$\operatorname{End}E\neq \mathbb{Z}$
(automatic if
$k$
is finite). Then every
$p$
-power order subgroup scheme
$G\subseteq E^{r}$
is a kernel subgroup.
Proof. The ring
$R:=\operatorname{End}E\simeq \operatorname{End}E_{\overline{k}}$
is a quadratic order. Although
$R$
is not necessarily a Dedekind domain, its conductor is prime to
$p$
, so it makes sense to speak of the splitting behavior of
$(p)$
in
$R$
. In fact, since
$E$
is ordinary,
$(p)$
splits, say as
$\mathfrak{p}\mathfrak{q}$
. So
$E[p]$
is the direct sum of group schemes
$E[\mathfrak{p}]$
and
$E[\mathfrak{q}]$
, each of order
$p$
by Theorem 4.4(e). Since
$E$
is ordinary, one of them, say
$E[\mathfrak{p}]$
, is étale, and the other is connected. For any
$e\in \mathbb{Z}_{{\geqslant}0}$
, we have
$(p^{e})=\mathfrak{p}^{e}\mathfrak{q}^{e}$
so
$E[p^{e}]\simeq E[\mathfrak{p}^{e}]\oplus E[\mathfrak{q}^{e}]$
. The Jordan–Hölder factors of
$E[\mathfrak{p}^{e}]$
are isomorphic to
$E[\mathfrak{p}]$
, so
$E[\mathfrak{p}^{e}]$
is étale; similarly
$E[\mathfrak{q}^{e}]$
is connected. We have
$G\subseteq E[p^{e}]^{r}$
for some
$e$
. By Proposition 6.2(c), we may assume that
$G\subseteq E[\mathfrak{p}^{e}]^{r}$
or
$G\subseteq E[\mathfrak{q}^{e}]^{r}$
.
In the first case,
$E[\mathfrak{p}^{e}](k^{s})\simeq \mathbb{Z}/p^{e}\mathbb{Z}$
, so
$G$
is the kernel of a homomorphism
$E[\mathfrak{p}^{e}]^{r}\rightarrow E[\mathfrak{p}^{e}]^{s}$
given by a matrix in
$\operatorname{M}_{s\times r}(\mathbb{Z})$
. Since
$E[\mathfrak{p}^{e}]$
is a kernel subgroup, so is
$E[\mathfrak{p}^{e}]^{r}$
, and so is
$G$
, by Propositions 6.2(a) and 6.3.
In the second case, we take Cartier duals:
$E[\mathfrak{p}^{e}]^{r}{\twoheadrightarrow}G^{\vee }$
. Then
$G^{\vee }$
is the cokernel of some homomorphism
$E[\mathfrak{p}^{e}]^{s}\rightarrow E[\mathfrak{p}^{e}]^{r}$
given by a matrix
$N\in \operatorname{M}_{r\times s}(\mathbb{Z})$
. So
$G$
is the kernel of the homomorphism
$E[\mathfrak{q}^{e}]^{r}\rightarrow E[\mathfrak{q}^{e}]^{s}$
given by the transpose
$N^{T}\in \operatorname{M}_{s\times r}(\mathbb{Z})$
. Since
$E[\mathfrak{q}^{e}]$
is a kernel subgroup, so is
$E[\mathfrak{q}^{e}]^{r}$
, and so is
$G$
, by Propositions 6.2(a) and 6.3.◻
Proposition 6.11. Let
$E$
be a supersingular elliptic curve over a field
$k$
of characteristic
$p$
.
(a) If
$k=\mathbb{F}_{p}$
, then every
$p$
-power order subgroup scheme
$G\subseteq E^{r}$
is a kernel subgroup, and in fact is a kernel of an endomorphism of
$E^{r}$
.(b) If
$k=\mathbb{F}_{p^{2}}$
and
$\operatorname{rk}R=4$
(i.e.,
$\#E(\mathbb{F}_{p^{2}})=(p\pm 1)^{2}$
), then every subgroup scheme
$G\subseteq E^{r}$
is a kernel subgroup.(c) If
$k=\mathbb{F}_{p^{2}}$
and
$\operatorname{rk}R\neq 4$
, then there exists a copy of
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
in
$E\times E$
that is not a kernel subgroup.(d) If
$k$
is
$\mathbb{F}_{p^{a}}$
for some
$a\geqslant 3$
, or if
$k$
is infinite, then there exists a copy of
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
in
$E\times E$
that is not a kernel subgroup.
Proof. The kernel of
$\unicode[STIX]{x1D70B}_{E,p}:E\rightarrow E^{(p)}$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
. Suppose that
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}\subseteq E$
is a kernel subgroup. By Proposition 6.3(i)
$\Rightarrow$
(iv),
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}\simeq \mathscr{H}\!\mathit{om}_{R}(R/I,E)$
for some left
$R$
-ideal
$I$
. By Theorem 4.4(e),
$p=\#(R/I)^{2/\text{rk}\,R}$
. We have three cases:
– If
$R=\mathbb{Z}$
, this is a contradiction.– If
$\operatorname{rk}R=2$
, then
$\#(R/I)=p$
, so
$R/I\simeq \mathbb{F}_{p}$
. Since
$E$
is supersingular,
$p$
is ramified or inert in
$R$
, and the above implies that
$p$
is ramified.– If
$\operatorname{rk}R=4$
, then
$\#(R/I)=p^{2}$
, so
$I$
is the unique ideal of index
$p^{2}$
in
$R$
, and
$R/I\simeq \mathbb{F}_{p^{2}}$
.
If
$J$
is an
$R$
-module with
$I^{2}\subsetneq J\subsetneq R^{2}$
(here
$I^{2}$
means
$I\times I$
), then
$R^{2}/J\simeq R/I$
(since
$R/I$
is a field), and the surjection
$R^{2}{\twoheadrightarrow}R^{2}/J$
gives rise to an injection
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}{\hookrightarrow}E\times E$
. Conversely, any kernel subgroup
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}\subseteq E\times E$
arises from such a
$J$
. So such kernel subgroups are in bijection with
$\mathbb{P}^{1}(R/I)$
. On the other hand,
$\operatorname{End}\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}\simeq k$
, so
$\operatorname{Hom}(\boldsymbol{\unicode[STIX]{x1D6FC}}_{p},E\times E)=k^{2}$
, and the copies of
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
in
$E\times E$
are in bijection with
$\mathbb{P}^{1}(k)$
. Thus if every
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
in
$E\times E$
is a kernel subgroup, then
$\mathbb{P}^{1}(R/I)$
is in bijection with
$\mathbb{P}^{1}(k)$
, so
$\#(R/I)=\#k$
; i.e.,
$k\simeq R/I$
, which is
$\mathbb{F}_{p}$
or
$\mathbb{F}_{p^{2}}$
as above. This proves (c) and (d).
(a) By Lemma 5.9,
$E^{r}\rightarrow E^{r}/G$
factors as a chain of
$p$
-isogenies, each with kernel
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
. If we show that any quotient
$E^{r}/\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
is isomorphic to
$E^{r}$
, then each abelian variety in the chain must be isomorphic to
$E^{r}$
, so
$G$
is a kernel of an endomorphism of
$E^{r}$
, as desired.
The group
$\text{GL}_{r}(\mathbb{Z})\subseteq \text{GL}_{r}(\operatorname{End}E)$
acts on
$E^{r}$
, and acts transitively on the nonzero elements of
$\operatorname{Hom}(\boldsymbol{\unicode[STIX]{x1D6FC}}_{p},E^{r})=\mathbb{F}_{p}^{r}$
. Therefore it suffices to consider the quotient
$E^{r}/\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
in which the
$\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}$
is contained in
$E\times 0\times \cdots \times 0$
. Now
$E/\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}=E/E[\unicode[STIX]{x1D70B}_{E}]\simeq E$
, so
$E^{r}/\boldsymbol{\unicode[STIX]{x1D6FC}}_{p}\simeq E^{r}$
.
(b) The abelian variety
$E^{r}/G$
is isogenous to a power of
$E$
, so by Theorem 5.3
(b), it is of the form
$\mathscr{H}\!\mathit{om}_{R}(M,E)$
. By Proposition 6.3(iii)
$\Rightarrow$
(i),
$G$
is a kernel subgroup.◻
7 Abelian varieties isogenous to a power of an elliptic curve
Let
$E$
be an elliptic curve over
$k$
. We break into cases, first according to whether
$E$
is ordinary or supersingular, and next according to
$\operatorname{rk}\operatorname{End}E$
and
$\#k$
. By convention, elliptic curves over a field of characteristic
$0$
are included among the ordinary curves.
7.1
$E$
is ordinary and
$\operatorname{rk}\operatorname{End}E=1$
Theorem 7.1. Fix an elliptic curve
$E$
over a field
$k$
such that
$\operatorname{End}E\simeq \mathbb{Z}$
.
(a) The image of
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
consists of abelian varieties isomorphic to a power of
$E$
.(b) The functors
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are inverse equivalences of categories (i.e., every abelian variety isogenous to a power of
$E$
is isomorphic to a power of
$E$
) if and only if
$\operatorname{char}k=0$
and for every prime
$\ell$
the homomorphism
$\mathbb{F}_{\ell }[{\mathcal{G}}_{k}]\rightarrow \operatorname{End}E[\ell ](k_{s})\simeq \operatorname{M}_{2}(\mathbb{F}_{\ell })$
is surjective.
Proof of Theorem 7.1.
(a) Every f.p. torsion-free
$\mathbb{Z}$
-module is free.
(b) By Proposition 6.4,
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are equivalences if and only if every finite subgroup scheme
$G$
is a kernel subgroup. By Proposition 6.2(c), we need only consider
$G$
of prime power order.
If
$\operatorname{char}k=p>0$
, then
$\#\ker \unicode[STIX]{x1D70B}_{E,p}=p$
, but
$\#E[I]$
is a square for every nonzero ideal
$I\subseteq \mathbb{Z}$
, so
$\ker \unicode[STIX]{x1D70B}_{E,p}$
is not a kernel subgroup. If
$\operatorname{char}k=0$
, then apply Proposition 6.9(i)
$\Leftrightarrow$
(iii) for every
$\ell$
.◻
Remark 7.2. Surjectivity of
$\mathbb{F}_{\ell }[{\mathcal{G}}_{k}]\rightarrow \operatorname{M}_{2}(\mathbb{F}_{\ell })$
fails if and only if the image
$G$
of
${\mathcal{G}}_{k}\rightarrow \text{GL}_{2}(\mathbb{F}_{\ell })$
is contained in a Borel subgroup or a nonsplit Cartan subgroup, as we now explain. Let
$A$
be the image of
$\mathbb{F}_{\ell }[{\mathcal{G}}_{k}]\rightarrow \operatorname{M}_{2}(\mathbb{F}_{\ell })$
. View
$V:=\mathbb{F}_{\ell }^{2}$
as an
$A$
-module. If
$V$
is reducible, then surjectivity fails and
$G$
is contained in a Borel subgroup. So suppose that
$V$
is irreducible. By Schur’s lemma [Reference LangLan02, XVII.1.1],
$\operatorname{End}_{A}V$
is a division algebra
$D$
. But
$D\subseteq \operatorname{M}_{2}(\mathbb{F}_{\ell })$
, so
$D$
is
$\mathbb{F}_{\ell }$
or
$\mathbb{F}_{\ell ^{2}}$
. By Wedderburn’s theorem [Reference LangLan02, XVII.3.5],
$A\simeq \operatorname{End}_{D}V$
. If
$D=\mathbb{F}_{\ell }$
, then
$A=\operatorname{M}_{2}(\mathbb{F}_{\ell })$
, and
$G$
is not contained in a Borel subgroup or a nonsplit Cartan subgroup. If
$D\simeq \mathbb{F}_{\ell ^{2}}$
, then
$\dim _{D}V=1$
, so
$A\simeq \operatorname{End}_{D}V\simeq \mathbb{F}_{\ell ^{2}}$
, and
$G$
is contained in the nonsplit Cartan subgroup
$A\cap \text{GL}_{2}(\mathbb{F}_{\ell })$
.
Example 7.3. Let
$E$
be the elliptic curve
$X_{0}(11)$
over
$\mathbb{Q}$
, with equation
$y^{2}+y=x^{3}-x^{2}-10x-20$
. As in [Reference SerreSer72, 5.5.2], the image of
${\mathcal{G}}_{\mathbb{Q}}\rightarrow \operatorname{Aut}E[5]\simeq \text{GL}_{2}(\mathbb{F}_{5})$
is contained in a Borel subgroup, so by Theorem 7.1(b) and Remark 7.2, the functors
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are not inverse equivalences of categories.
Example 7.4. Let
$E$
be the elliptic curve over
$\mathbb{Q}$
of conductor
$37$
with equation
$y^{2}+y=x^{3}-x$
. By [Reference SerreSer72, 5.5.6], the homomorphism
${\mathcal{G}}_{\mathbb{Q}}\rightarrow \operatorname{Aut}(E[\ell ])\simeq \text{GL}_{2}(\mathbb{F}_{\ell })$
is surjective for every prime
$\ell$
, so by Theorem 7.1(b), the functors
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are inverse equivalences of categories.
7.2
$E$
is ordinary and
$\operatorname{rk}\operatorname{End}E=2$
Fix an ordinary elliptic curve
$E$
over a field
$k$
such that
$\operatorname{rk}\operatorname{End}E=2$
. (These are called CM elliptic curves in [Reference KaniKan11, §3].) Then
$\operatorname{End}E\simeq \operatorname{End}E_{\overline{k}}$
, because if an endomorphism becomes divisible by a positive integer
$n$
over an extension field, it kills
$E[n]$
, so it is divisible by
$n$
already over
$k$
. Let
$R:=\operatorname{End}E$
and
$K:=\operatorname{Frac}R$
.
If
$E^{\prime }$
is an elliptic curve isogenous to
$E$
, then
$\operatorname{End}E^{\prime }$
is another order
$R^{\prime }$
in
$K$
. Let
$f_{E^{\prime }}$
be the conductor of
$R^{\prime }$
, i.e., the index of
$R^{\prime }$
in its integral closure. More generally, if
$A$
is an abelian variety isogenous to
$E^{r}$
, then
$\operatorname{End}A$
is an order in
$M_{r}(K)$
, and its center
$Z(\operatorname{End}A)$
is an order in
$Z(M_{r}(K))=K$
, and we let
$f_{A}$
be the conductor of
$Z(\operatorname{End}A)$
.
Theorem 7.5. Fix an ordinary elliptic curve
$E$
over a field
$k$
such that
$\operatorname{rk}\operatorname{End}E=2$
. Let
$R:=\operatorname{End}E$
. The image of
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
consists of the abelian varieties
$A$
isogenous to a power of
$E$
such that
$f_{A}|f_{E}$
, i.e., such that
$R\subseteq Z(\operatorname{End}A)$
. These are exactly the products of elliptic curves
$E^{\prime }$
each isogenous to
$E$
and satisfying
$f_{E^{\prime }}|f_{E}$
.
Proof. Suppose that
$\unicode[STIX]{x1D719}:E^{r}\rightarrow A$
is an isogeny and
$f_{A}|f_{E}$
. Since
$f_{A}|f_{E}$
, there is an
$R$
-action on
$A$
such that
$\unicode[STIX]{x1D719}$
respects the
$R$
-actions. Let
$G:=\ker \unicode[STIX]{x1D719}$
, so
$G(k_{s})$
is an
$R$
-module. Write
$G=\bigoplus _{\ell }G_{\ell }$
, where
$G_{\ell }$
is a group scheme of
$\ell$
-power order. For
$\ell \neq \operatorname{char}k$
, we are in the case
$R_{\ell }=C$
of § 6.3, so
$G_{\ell }(k_{s})$
is also a
$C/\ell ^{e}C$
-module for some
$e$
, and Proposition 6.8 shows that
$G_{\ell }$
is a kernel subgroup. If
$\operatorname{char}k=p>0$
, then
$G_{p}$
is a kernel subgroup by Proposition 6.10. By Proposition 6.2(c),
$G$
is a kernel subgroup. By Proposition 6.3(i)
$\Rightarrow$
(iii), the abelian variety
$A\simeq E^{r}/G$
is in the image of
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
.
Conversely, if
$A$
is in the image of
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
, then by Theorem 4.8(c)
$A$
is a product of elliptic curves of the form
$\mathscr{H}\!\mathit{om}_{R}(I,E)$
. Because the functor
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is fully faithful, if
$E^{\prime }=\mathscr{H}\!\mathit{om}_{R}(I,E)$
then
$E^{\prime }$
is isogenous to
$E$
and
$\operatorname{End}E^{\prime }\simeq \operatorname{End}_{R}I$
, which contains
$R$
since
$R$
is commutative. In particular,
$f_{E^{\prime }}|f_{E}$
. Finally,
$f_{A}$
is the least common multiple of the
$f_{E^{\prime }}$
, so
$f_{A}|f_{E}$
too.◻
Theorem 7.6. Fix an ordinary elliptic curve
$E$
over a finite field
$\mathbb{F}_{q}$
. Let
$R:=\operatorname{End}E$
. Then
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are equivalences of categories if and only if
$\mathbb{Z}[\unicode[STIX]{x1D70B}_{E}]=R$
.
Proof. Suppose that
$\mathbb{Z}[\unicode[STIX]{x1D70B}_{E}]=R$
. If
$A$
is isogenous to a power of
$E$
, then
$\unicode[STIX]{x1D70B}_{A}$
has the same minimal polynomial as
$\unicode[STIX]{x1D70B}_{E}$
, so
$Z(\operatorname{End}A)$
contains
$\mathbb{Z}[\unicode[STIX]{x1D70B}_{A}]\simeq \mathbb{Z}[\unicode[STIX]{x1D70B}_{E}]$
; i.e.,
$f_{A}|f_{E}$
is automatic.
On the other hand, if
$\mathbb{Z}[\unicode[STIX]{x1D70B}_{E}]\neq R$
, then
$E$
is isogenous to an elliptic curve
$E^{\prime }$
satisfying
$\operatorname{End}E^{\prime }=\mathbb{Z}[\unicode[STIX]{x1D70B}_{E^{\prime }}]$
[Reference WaterhouseWat69, Theorem 4.2(2)]. Theorem 7.5 shows that
$E^{\prime }$
is not in the image of
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
, so
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
is not an equivalence of categories.◻
We can also give a more general criterion that applies even if
$k$
is not finite.
Theorem 7.7. Fix an ordinary elliptic curve
$E$
over a field
$k$
such that
$\operatorname{rk}\operatorname{End}E=2$
. Then
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are equivalences of categories if and only if for every prime
$\ell \neq \operatorname{char}k$
, there exists
$\unicode[STIX]{x1D70E}\in {\mathcal{G}}_{k}$
whose action on
$E[\ell ](k_{s})$
is not multiplication by a scalar.
Proof. By Propositions 6.4(i)
$\Leftrightarrow$
(iii), 6.2(c), and 6.10, the functors
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are equivalences if and only if, for each
$\ell \neq \operatorname{char}k$
, the homomorphism
$\mathbb{F}_{\ell }[{\mathcal{G}}_{k}]\rightarrow C/\ell C$
is surjective. Since
$\dim _{\mathbb{F}_{\ell }}C/\ell C=2$
, surjectivity is equivalent to the image of
$$\begin{eqnarray}\mathbb{F}_{\ell }[{\mathcal{G}}_{k}]\longrightarrow C/\ell C\subseteq \operatorname{End}E[\ell ](k_{s})\simeq \operatorname{M}_{2}(\mathbb{F}_{\ell })\end{eqnarray}$$
not being
$\mathbb{F}_{\ell }$
.◻
Example 7.8. Let
$E$
be the elliptic curve
$y^{2}=x^{3}-x$
over
$k:=\mathbb{Q}(\sqrt{-1})$
; then
$j(E)=1728$
and
$\operatorname{End}E=\mathbb{Z}[\sqrt{-1}]$
. The group
${\mathcal{G}}_{k}$
acts trivially on
$E[2](k_{s})$
, so by Theorem 7.7, the functors
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are not inverse equivalences of categories.
Example 7.9. Let
$E$
be the elliptic curve
$y^{2}=x^{3}+x^{2}-3x+1$
over
$k:=\mathbb{Q}(\sqrt{-2})$
; then
$j(E)=8000$
and
$\operatorname{End}E=\mathbb{Z}[\sqrt{-2}]$
. The field
$k(E[2])$
equals
$k(\sqrt{-1})$
, so the image of
${\mathcal{G}}_{k}$
in
$\text{GL}_{2}(\mathbb{F}_{2})$
has order
$2$
and hence does not consist of scalars. Now consider a prime
$\ell >2$
. Choose a prime
$p\neq \ell$
such that
$p$
splits in
$k/\mathbb{Q}$
and
$(p/\ell )=-1$
. Let
$\unicode[STIX]{x1D70E}$
be a Frobenius element of
${\mathcal{G}}_{k}$
at a prime above
$p$
. The image of
$\unicode[STIX]{x1D70E}$
in
$\operatorname{Aut}(E[\ell ])\simeq \text{GL}_{2}(\mathbb{F}_{\ell })$
has nonsquare determinant
$(p\hspace{0.2em}{\rm mod}\hspace{0.2em}\ell )$
, so it is not a scalar. Thus, by Theorem 7.7, the functors
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are inverse equivalences of categories.
Remark 7.10. If
$E$
and
$E^{\prime }$
are ordinary elliptic curves over an algebraically closed field
$k$
and their endomorphism rings are orders in the same quadratic field, then
$E$
and
$E^{\prime }$
are isogenous. But over non-algebraically closed fields, this can fail. For example, if
$E$
is an ordinary elliptic curve over a finite field, then its quadratic twist
$E^{\prime }$
has the same endomorphism ring, but opposite trace of Frobenius, so
$E$
and
$E^{\prime }$
are not isogenous.
7.3
$E$
is supersingular and
$k=\mathbb{F}_{p}$
Fix a supersingular elliptic curve
$E$
over
$\mathbb{F}_{p}$
. Let
$R:=\operatorname{End}E$
. Let
$P(x)$
be the characteristic polynomial of
$\unicode[STIX]{x1D70B}:=\unicode[STIX]{x1D70B}_{E}$
. Define
$f_{A}$
as in § 7.2. In particular,
$f_{E}$
is the conductor of
$R$
. We have the following cases:
The last column, which indicates when
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are equivalences of categories, is explained by the following analogues of Theorems 7.5 and 7.6, proved in the same way except that we use Proposition 6.11(a) in place of Proposition 6.10.
Theorem 7.11. Fix a supersingular elliptic curve
$E$
over
$\mathbb{F}_{p}$
. Let
$R:=\operatorname{End}E$
. The image of
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
consists of the abelian varieties
$A$
isogenous to a power of
$E$
such that
$f_{A}|f_{E}$
, i.e., such that
$R\subseteq Z(\operatorname{End}A)$
. These are exactly the products of elliptic curves
$E^{\prime }$
each isogenous to
$E$
and satisfying
$f_{E^{\prime }}|f_{E}$
.
Theorem 7.12. Fix a supersingular elliptic curve
$E$
over
$\mathbb{F}_{p}$
. Let
$R:=\operatorname{End}E$
. Then the functors
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are equivalences of categories if and only if
$\mathbb{Z}[\unicode[STIX]{x1D70B}_{E}]=R$
.
7.4
$E$
is supersingular,
$k=\mathbb{F}_{p^{2}}$
, and
$\operatorname{rk}\operatorname{End}E=4$
In this case,
$E$
is a maximal or minimal elliptic curve over
$\mathbb{F}_{p^{2}}$
. These cases were already handled: see Theorem 5.3.
7.5
$E$
is supersingular,
$k=\mathbb{F}_{p^{2}}$
, and
$\operatorname{rk}\operatorname{End}E=2$
By Proposition 6.11(c), not every subgroup scheme is a kernel subgroup. By Proposition 6.4(iii)
$\Leftrightarrow$
(ii), the functors
$\mathscr{H}\!\mathit{om}_{R}(-,E)$
and
$\operatorname{Hom}(-,E)$
are not equivalences of categories.
Remark 7.13. These are the cases in which the characteristic polynomial of
$\unicode[STIX]{x1D70B}_{E}$
is one of
$x^{2}+px+p^{2}$
,
$x^{2}+p^{2}$
, or
$x^{2}-px+p^{2}$
. Hence
$\unicode[STIX]{x1D70B}_{E}=p\unicode[STIX]{x1D701}$
for a root of unity
$\unicode[STIX]{x1D701}$
of order
$3$
,
$4$
, or
$6$
, respectively. But
$p$
does not divide the conductor of
$R$
, so
$\unicode[STIX]{x1D701}\in R$
. Now
$\unicode[STIX]{x1D701}\in \operatorname{Aut}E$
, so
$E$
has
$j$
-invariant
$0$
or
$1728$
.
8 A partial generalization to higher-dimensional abelian varieties over
$\mathbb{F}_{p}$
Let
$B$
be an abelian variety over a prime field
$\mathbb{F}_{p}$
. Let
$R\subseteq \operatorname{End}B$
be the (central) subring
$\mathbb{Z}[F,V]$
generated by the Frobenius and Verschiebung endomorphisms. Given a f.p. reflexive
$R$
-module
$M$
, let
$M^{\ast }:=\operatorname{Hom}_{R}(M,R)$
; then
$M^{\ast }$
is reflexive too.
As in the case of elliptic curves, we can define functors
$$\begin{eqnarray}\mathscr{H}\!\mathit{om}_{R}(-,B):\{\text{f.p. }R\text{-modules}\}^{\operatorname{opp}}\longrightarrow \{\text{commutative proper group schemes over }\mathbb{F}_{p}\}\end{eqnarray}$$
and
$$\begin{eqnarray}\operatorname{Hom}(-,B):\{\text{commutative proper group schemes over }\mathbb{F}_{p}\}\longrightarrow \{\text{f.p. }R\text{-modules}\}^{\operatorname{opp}}.\end{eqnarray}$$
The work of Centeleghe and Stix [Reference Centeleghe and StixCS15], combined with some further arguments, allows us to analyze this higher-dimensional case. The main extra ingredient we supply is that, under appropriate hypotheses, the functor
$M\mapsto M^{\ast }\otimes _{R}B$
implicit in [Reference Centeleghe and StixCS15] is isomorphic to
$\mathscr{H}\!\mathit{om}_{R}(-,B)$
.
Theorem 8.1. Let
$B$
be an abelian variety over
$\mathbb{F}_{p}$
. Let
$R=\mathbb{Z}[F,V]\subseteq \operatorname{End}B$
. Then the functors
$\mathscr{H}\!\mathit{om}_{R}(-,B)$
and
$\operatorname{Hom}(-,B)$
restrict to inverse equivalences of categories
if and only if
$R=\operatorname{End}B$
. Moreover, in this case, the functor
$\mathscr{H}\!\mathit{om}_{R}(-,B)$
so restricted is exact, and it is isomorphic to the functor
$M\mapsto M^{\ast }\otimes B$
.
Proof. If the functors give inverse equivalences as stated, then the argument in the paragraph before Theorem 4.8 proves that
$R=\operatorname{End}B$
.
Now let us prove the converse. Suppose that
$R=\operatorname{End}B$
. Then
$(\operatorname{End}B)\otimes \mathbb{Q}$
is commutative. This implies that, in the decomposition of
$B$
into simple factors up to isogeny, no factor is repeated, and also no factor is associated to the Weil number
$\sqrt{p}$
, since such a factor would give a direct factor of
$(\operatorname{End}B)\otimes \mathbb{Q}$
isomorphic to a quaternion algebra over
$\mathbb{Q}(\sqrt{p})$
; see [Reference WaterhouseWat69, p. 528, Case 2]. Let
$w$
be the set of Weil number conjugacy classes associated to
$B$
. Then the category
$\text{AV}_{w}$
of [Reference Centeleghe and StixCS15, 5.1] is the category of abelian variety quotients of powers of
$B$
. The ring
$R_{w}$
in [Reference Centeleghe and StixCS15, Definition 2] is
$R=\mathbb{Z}[F,V]$
. It is Gorenstein by [Reference Centeleghe and StixCS15, Theorem 11(2)]. Reflexive finitely generated
$R$
-modules are the same as f.p. torsion-free
$R$
-modules, or equivalently f.p.
$R$
-modules that are free over
$\mathbb{Z}$
[Reference Centeleghe and StixCS15, Lemma 13]. By [Reference Centeleghe and StixCS15, Proposition 24], for every prime
$\ell$
the
$(R\otimes \mathbb{Z}_{\ell })$
-module
$T_{\ell }B$
(Tate module or contravariant Dieudonné module) is free of rank
$1$
, so the abelian variety
$A_{w}$
in [Reference Centeleghe and StixCS15, Proposition 21] may be taken to be
$B$
by [Reference Centeleghe and StixCS15, Proposition 24].
We now check that if
$M$
is a f.p. torsion-free
$R$
-module, then the commutative proper group scheme
$G:=\mathscr{H}\!\mathit{om}_{R}(M,B)$
is an abelian variety. It suffices to prove that for every prime
$\ell$
and
$n\geqslant 0$
, the homomorphism
$G[\ell ^{n+1}]\stackrel{\ell }{\rightarrow }G[\ell ^{n}]$
is surjective. Choose a presentation
$R^{a}\stackrel{N}{\rightarrow }R^{b}\rightarrow M\rightarrow 0$
, so
$G:=\ker (B^{b}\rightarrow B^{a})$
. Both
$M$
and
$M^{\ast }$
are reflexive
$R$
-modules, so they are free over
$\mathbb{Z}$
.
Suppose that
$\ell \neq p$
. Then
$$\begin{eqnarray}\displaystyle G[\ell ^{n}] & = & \displaystyle (\ker (B^{b}\rightarrow B^{a}))[\ell ^{n}]\nonumber\\ \displaystyle & = & \displaystyle \ker (B^{b}[\ell ^{n}]\rightarrow B^{a}[\ell ^{n}])\nonumber\\ \displaystyle & \simeq & \displaystyle \ker (T_{\ell }(B^{b})/\ell ^{n}\rightarrow T_{\ell }(B^{a})/\ell ^{n})\nonumber\\ \displaystyle & = & \displaystyle \ker ((R/\ell ^{n})^{b}\stackrel{N^{T}}{\rightarrow }(R/\ell ^{n})^{a})\nonumber\\ \displaystyle & = & \displaystyle \ker (\operatorname{Hom}_{R}(R^{b},R/\ell ^{n})\stackrel{N^{T}}{\rightarrow }\operatorname{Hom}_{R}(R^{a},R/\ell ^{n}))\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{Hom}_{R}(M,R/\ell ^{n})\nonumber\\ \displaystyle & \simeq & \displaystyle M^{\ast }/\ell ^{n}\quad (\text{since }\operatorname{Ext}_{R}^{1}(M,R)=0\text{ by [CS15, Lemma 17]})\nonumber\\ \displaystyle & = & \displaystyle M^{\ast }\underset{\mathbb{Z}}{\otimes }\frac{\ell ^{-n}\mathbb{Z}}{\mathbb{Z}}.\nonumber\end{eqnarray}$$
Since
$M^{\ast }$
is free over
$\mathbb{Z}$
, the homomorphism
$$\begin{eqnarray}M^{\ast }\underset{\mathbb{Z}}{\otimes }\frac{\ell ^{-(n+1)}\mathbb{Z}}{\mathbb{Z}}\stackrel{\ell }{\longrightarrow }M^{\ast }\underset{\mathbb{Z}}{\otimes }\frac{\ell ^{-n}\mathbb{Z}}{\mathbb{Z}}\end{eqnarray}$$
is surjective, so
$G[\ell ^{n+1}]\stackrel{\ell }{\rightarrow }G[\ell ^{n}]$
is surjective.
Now suppose that
$\ell =p$
. For each commutative group scheme
$H$
over
$\mathbb{F}_{p}$
, let
$H^{D}$
denote its contravariant Dieudonné module. Since the
$R\otimes \mathbb{Z}_{p}$
-module
$T_{p}B$
is free of rank
$1$
, we have
$B[p^{n}]^{D}\simeq R/p^{n}$
as an
$R$
-module. Next,
$$\begin{eqnarray}\displaystyle G[p^{n}]^{D} & = & \displaystyle \operatorname{coker}(B^{a}[p^{n}]^{D}\rightarrow B^{b}[p^{n}]^{D})\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{coker}((R/p^{n})^{a}\stackrel{N}{\rightarrow }(R/p^{n})^{b})\nonumber\\ \displaystyle & = & \displaystyle M/p^{n}.\nonumber\end{eqnarray}$$
Since
$M$
is free over
$\mathbb{Z}$
, the homomorphism
$M/p^{n}\stackrel{p}{\rightarrow }M/p^{n+1}$
is injective, so
$G[p^{n}]^{D}\stackrel{p}{\rightarrow }G[p^{n+1}]^{D}$
is injective, so
$G[p^{n+1}]\stackrel{p}{\rightarrow }G[p^{n}]$
is surjective.
Thus
$G$
is an abelian variety. The proof of Theorem 4.4(b) now shows that
$\mathscr{H}\!\mathit{om}_{R}(-,B)$
is exact. In particular, if
$0\rightarrow M\rightarrow R^{n}\rightarrow R^{m}$
is an exact sequence of
$R$
-modules, then
$B^{m}\rightarrow B^{n}\rightarrow \mathscr{H}\!\mathit{om}_{R}(M,B)\rightarrow 0$
is exact. But
$M^{\ast }\otimes B$
too is defined as
$\operatorname{coker}(B^{m}\rightarrow B^{n})$
, so
$\mathscr{H}\!\mathit{om}_{R}(M,B)\simeq M^{\ast }\otimes _{R}B$
, and this holds functorially in
$M$
.
Finally, by [Reference Centeleghe and StixCS15, Theorem 25 and p. 247],
$$\begin{eqnarray}\operatorname{Hom}(-,B):\text{AV}_{w}\longrightarrow \{\text{f.p. reflexive }R\text{-modules}\}^{\operatorname{opp}}\end{eqnarray}$$
is an equivalence of categories with inverse functor
$M\mapsto M^{\ast }\otimes _{R}B$
. We may replace the latter with the isomorphic functor
$\mathscr{H}\!\mathit{om}_{R}(-,B)$
.◻
Remark 8.2. Over
$\mathbb{F}_{p^{n}}$
with
$n>1$
, the functors
$\mathscr{H}\!\mathit{om}_{R}(-,B)$
and
$\operatorname{Hom}(-,B)$
are sometimes inverse equivalences of categories, and sometimes not, as we saw already in the case of elliptic curves; see Theorem 1.1.
Acknowledgements
It is a pleasure to thank Everett Howe, Tony Scholl, and Christopher Skinner for helpful discussions. We thank also the referees for valuable suggestions on the exposition.
