Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Xiantao
and
Ming, Pingbing
2014.
A Study on the Quasi-continuum Approximations of a One-Dimensional Fracture Model.
Multiscale Modeling & Simulation,
Vol. 12,
Issue. 3,
p.
1379.
2015.
Discrete‐Continuum Coupling Method to Simulate Highly Dynamic Multi‐Scale Problems.
p.
171.
Jebahi, Mohamed
Dau, Frédéric
Charles, Jean-Luc
and
Iordanoff, Ivan
2016.
Multiscale Modeling of Complex Dynamic Problems: An Overview and Recent Developments.
Archives of Computational Methods in Engineering,
Vol. 23,
Issue. 1,
p.
101.
Gooneie, Ali
Schuschnigg, Stephan
and
Holzer, Clemens
2017.
A Review of Multiscale Computational Methods in Polymeric Materials.
Polymers,
Vol. 9,
Issue. 1,
p.
16.
Chu, Weiqi
and
Li, Xiantao
2018.
On the Asymptotic Behavior of the Kernel Function in the Generalized Langevin Equation: A One-Dimensional Lattice Model.
Journal of Statistical Physics,
Vol. 170,
Issue. 2,
p.
378.
Manolis, George D.
Dineva, Petia S.
Rangelov, Tsviatko
and
Sfyris, Dimitris
2021.
Mechanical models and numerical simulations in nanomechanics: A review across the scales.
Engineering Analysis with Boundary Elements,
Vol. 128,
Issue. ,
p.
149.
Kim, Woo Kyun
Kavalur, Aditya
Whalen, Stephen M.
and
Tadmor, Ellad B.
2022.
Free energy calculation and ghost force correction for hot‐QC.
International Journal for Numerical Methods in Engineering,
Vol. 123,
Issue. 20,
p.
4916.
Wei, Xindong
Li, Zhe
and
Zhao, Gaofeng
2024.
A review of multiscale numerical modeling of rock mechanics and rock engineering.
Deep Underground Science and Engineering,
Tang, Mingjian
Shuang, Fei
and
Xiao, Pan
2024.
Enhanced fast inertial relaxation engine (FIRE) for multiscale simulations.
Computational Materials Science,
Vol. 244,
Issue. ,
p.
113234.
Kienzlen, A.
and
Verl, A.
2024.
Production at the Leading Edge of Technology.
p.
491.
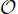 (ε) and the time scale
(ε) and the time scale 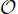 (1) with ε being the lattice spacing.
(1) with ε being the lattice spacing.

