Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-23T12:43:07.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Vicarious Graphs

Published online by Cambridge University Press:  13 November 2009

TOMASZ ŁUCZAK  and
ANDREW THOMASON
TOMASZ ŁUCZAK
Affiliation:
Faculty of Mathematics and Computer Science, Adam Mickiewicz University, Poznań, Poland (e-mail: tomasz@amu.edu.pl)
ANDREW THOMASON
Affiliation:
DPMMS, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WB, UK (e-mail: A.G.Thomason@dpmms.cam.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let H be some fixed graph. We call a graph Gvicarious for H if G is maximal H-free and, for every edge e of G, there is an edge f not in G such that G − e + f is also H-free. We demonstrate various properties of vicarious graphs and several examples are given. It is conjectured that a graph of order n which is vicarious for K3 has size at most (1/4 + o(1))().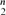

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 19 , Issue 5-6: Papers from the 2009 Oberwolfach Meeting on Combinatorics and Probability , November 2010 , pp. 819 - 827
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Erdős, P. (1967) Some recent results on extremal problems in graph theory: Results. In Theory of Graphs, Proc. International Symposium, Rome 1966 (Rosenstiehl, P., ed.), Gordon and Breach, New York, Dunod, Paris, pp. 118–123.Google Scholar
[2]Erdős, P. (1968) On some new inequalities concerning extremal properties of graphs. In Theory of Graphs, Proc. Colloquium, Tihany 1966 (Erdős, P. and Katona, G., eds), Academic Press, New York, pp. 77–81.Google Scholar
[3]Erdős, P., Faudree, R. J., Gyárfás, A. and Schelp, R. H. (1991) Odd cycles in graphs of given minimum degree. In Graph Theory, Combinatorics and Applications, Vol. 1, Proc. International Conference, Kalamazoo 1988, Wiley-Interscience, New York, pp. 407–418.Google Scholar
[4]Simonovits, M. (1968) A method for solving extremal problems in graph theory, stability problems. In Theory of Graphs, Proc. Colloquium, Tihany 1966 (Erdős, P. and Katona, G., eds), Academic Press, New York, pp. 279–319.Google Scholar