Article contents
Marstrand-type Theorems for the Counting and Mass Dimensions in ℤ
Published online by Cambridge University Press: 16 March 2016
Abstract
The counting and (upper) mass dimensions of a set A ⊆ 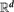 $\mathbb{R}^d$ are
$\mathbb{R}^d$ are
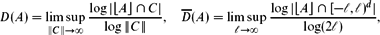 $$D(A) = \limsup_{\|C\| \to \infty} \frac{\log | \lfloor A \rfloor \cap C |}{\log \|C\|}, \quad \smash{\overline{D}}\vphantom{D}(A) = \limsup_{\ell \to \infty} \frac{\log | \lfloor A \rfloor \cap [-\ell,\ell)^d |}{\log (2 \ell)},$$
$$D(A) = \limsup_{\|C\| \to \infty} \frac{\log | \lfloor A \rfloor \cap C |}{\log \|C\|}, \quad \smash{\overline{D}}\vphantom{D}(A) = \limsup_{\ell \to \infty} \frac{\log | \lfloor A \rfloor \cap [-\ell,\ell)^d |}{\log (2 \ell)},$$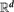 $\mathbb{R}^d$ with side length ‖C‖ → ∞. We give a characterization of the counting dimension via coverings:
$\mathbb{R}^d$ with side length ‖C‖ → ∞. We give a characterization of the counting dimension via coverings:
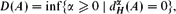 $$D(A) = \text{inf} \{ \alpha \geq 0 \mid {d_{H}^{\alpha}}(A) = 0 \},$$
$$D(A) = \text{inf} \{ \alpha \geq 0 \mid {d_{H}^{\alpha}}(A) = 0 \},$$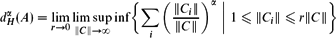 $${d_{H}^{\alpha}}(A) = \lim_{r \rightarrow 0} \limsup_{\|C\| \rightarrow \infty} \inf \biggl\{ \sum_i \biggl(\frac{\|C_i\|}{\|C\|} \biggr)^\alpha
\ \bigg| \
1 \leq \|C_i\| \leq r \|C\| \biggr\}$$
$${d_{H}^{\alpha}}(A) = \lim_{r \rightarrow 0} \limsup_{\|C\| \rightarrow \infty} \inf \biggl\{ \sum_i \biggl(\frac{\|C_i\|}{\|C\|} \biggr)^\alpha
\ \bigg| \
1 \leq \|C_i\| \leq r \|C\| \biggr\}$$ $\mathbb{R}^d$ under orthogonal projections with range of dimension k have counting dimension at least min(k, D(A)); if we assume D(A) = D(A), then the mass dimension of A under the typical orthogonal projection is equal to min(k, D(A)). This work extends recent work of Y. Lima and C. G. Moreira.
$\mathbb{R}^d$ under orthogonal projections with range of dimension k have counting dimension at least min(k, D(A)); if we assume D(A) = D(A), then the mass dimension of A under the typical orthogonal projection is equal to min(k, D(A)). This work extends recent work of Y. Lima and C. G. Moreira.
MSC classification
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2016
References
- 5
- Cited by




