Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T20:56:52.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Inapproximability of the Partition Function for the Antiferromagnetic Ising and Hard-Core Models

Part of: Equilibrium statistical mechanics Graph theory Theory of computing Markov processes

Published online by Cambridge University Press:  02 February 2016

ANDREAS GALANIS ,
DANIEL ŠTEFANKOVIČ  and
ERIC VIGODA
ANDREAS GALANIS
Affiliation:
School of Computer Science, Georgia Institute of Technology, Atlanta, GA 30332, USA (email: andreas.galanis@cs.ox.ac.uk, vigoda@cc.gatech.edu)
DANIEL ŠTEFANKOVIČ
Affiliation:
Department of Computer Science, University of Rochester, Rochester, NY 14627, USA (email: stefanko@cs.rochester.edu)
ERIC VIGODA
Affiliation:
School of Computer Science, Georgia Institute of Technology, Atlanta, GA 30332, USA (email: andreas.galanis@cs.ox.ac.uk, vigoda@cc.gatech.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent inapproximability results of Sly (2010), together with an approximation algorithm presented by Weitz (2006), establish a beautiful picture of the computational complexity of approximating the partition function of the hard-core model. Let λc(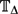$\mathbb{T}_{\Delta}$) denote the critical activity for the hard-model on the infinite Δ-regular tree. Weitz presented an FPTAS for the partition function when λ < λc(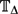$\mathbb{T}_{\Delta}$) for graphs with constant maximum degree Δ. In contrast, Sly showed that for all Δ ⩾ 3, there exists εΔ > 0 such that (unless RP = NP) there is no FPRAS for approximating the partition function on graphs of maximum degree Δ for activities λ satisfying λc(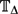$\mathbb{T}_{\Delta}$) < λ < λc(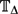$\mathbb{T}_{\Delta}$) + εΔ.

We prove that a similar phenomenon holds for the antiferromagnetic Ising model. Sinclair, Srivastava and Thurley (2014) extended Weitz's approach to the antiferromagnetic Ising model, yielding an FPTAS for the partition function for all graphs of constant maximum degree Δ when the parameters of the model lie in the uniqueness region of the infinite Δ-regular tree. We prove the complementary result for the antiferromagnetic Ising model without external field, namely, that unless RP = NP, for all Δ ⩾ 3, there is no FPRAS for approximating the partition function on graphs of maximum degree Δ when the inverse temperature lies in the non-uniqueness region of the infinite tree 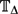$\mathbb{T}_{\Delta}$. Our proof works by relating certain second moment calculations for random Δ-regular bipartite graphs to the tree recursions used to establish the critical points on the infinite tree.

MSC classification

Primary: 68Q87: Probability in computer science (algorithm analysis, random structures, phase transitions, etc.)
Secondary: 82B20: Lattice systems (Ising, dimer, Potts, etc.) and systems on graphs 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 05C80: Random graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 4 , July 2016 , pp. 500 - 559
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Achlioptas, D. and Naor, A. (2005) The two possible values of the chromatic number of a random graph. Ann. of Math. 162 1333–1349.Google Scholar
[2] Achlioptas, D. and Peres, Y. (2004) The threshold for random k-SAT is 2 k log 2 - O(k). J. Amer. Math. Soc. 17 947–973.CrossRefGoogle Scholar
[3] Beffara, V. and Duminil-Copin, H. (2012) The self-dual point of the two-dimensional random cluster model is critical for q ⩾ 1. Probab. Theory Rel. Fields 153 511–542.Google Scholar
[4] de Bruijn, N. G. (1981) Asymptotic Methods in Analysis, Dover.Google Scholar
[5] Cai, J.-Y., Galanis, A., Goldberg, L. A., Guo, H., Jerrum, M., Štefankovič, D. and Vigoda, E. (2014) #BIS-hardness for 2-spin systems on bipartite bounded degree graphs in the tree non-uniqueness region. In Proc. 18th International Workshop on Randomization and Computation (RANDOM), pp. 582–595.Google Scholar
[6] Dembo, A., Montanari, A. and Sun, N. (2013) Factor models on locally tree-like graphs. Ann. Probab. 41 4162–4213.Google Scholar
[7] Dyer, M., Frieze, A. M. and Jerrum, M. (2002) On counting independent sets in sparse graphs. SIAM J. Comput. 31 1527–1541.CrossRefGoogle Scholar
[8] Galanis, A., Ge, Q., Štefankovič, D., Vigoda, E. and Yang, L. (2014) Improved inapproximability results for counting independent sets in the hard-core model. Random Struct. Alg. 45 78–110.CrossRefGoogle Scholar
[9] Galanis, A., Štefankovič, D. and Vigoda, E. (2012) Inapproximability of the partition function for the antiferromagnetic Ising and hard-core models. arXiv.org:1203.2226 Google Scholar
[10] Galanis, A., Štefankovič, D. and Vigoda, E. (2014) Inapproximability for antiferromagnetic spin systems in the tree non-uniqueness region. In Proc. 46th Annual ACM Symposium on Theory of Computing (STOC). 62 pp. 823–831. http://dl.acm.org/citation.cfm?doid=2785964 Google Scholar
[11] Georgii, H.-O. (1988) Gibbs Measures and Phase Transitions , Vol. 9 of De Gruyter Studies in Mathematics, Walter de Gruyter.Google Scholar
[12] Goldberg, L. A., Jerrum, M. and Paterson, M. (2003) The computational complexity of two-state spin systems. Random Struct. Alg. 23 133–154.CrossRefGoogle Scholar
[13] Greenhill, C. (2000) The complexity of counting colorings and independent sets in sparse graphs and hypergraphs. Comput. Complexity 9 52–72.Google Scholar
[14] Janson, S. (1995) Random regular graphs: Asymptotic distributions and contiguity. Combin. Probab. Comput. 4 369–405.Google Scholar
[15] Janson, S., Łuczak, T. and Rucinski, A. (2000) Random Graphs, Wiley-Interscience.CrossRefGoogle Scholar
[16] Jerrum, M. and Sinclair, A. (1993) Polynomial-time approximation algorithms for the Ising model. SIAM J. Comput. 22 1087–1116.Google Scholar
[17] Kelly, F. P. (1985) Stochastic models of computer communication systems. J. Royal Statist. Soc. Ser. B 47 379–395.Google Scholar
[18] Li, L., Lu, P. and Yin, Y. (2013) Correlation decay up to uniqueness in spin systems. In Proc. 24th Annual ACM–SIAM Symposium on Discrete Algorithms (SODA), pp. 47–66.Google Scholar
[19] Martinelli, F., Sinclair, A. and Weitz, D. (2004) Glauber dynamics on trees: Boundary conditions and mixing time. Comm. Math. Phys. 250 301–334.CrossRefGoogle Scholar
[20] Martinelli, F., Sinclair, A. and Weitz, D. (2007) Fast mixing for independent sets, colorings, and other models on trees. Random Struct. Alg. 31 134–172.Google Scholar
[21] Mezard, M. and Montanari, A. (2009) Information, Physics, and Computation, Oxford University Press.CrossRefGoogle Scholar
[22] Molloy, M., Robalewska, H., Robinson, R. W. and Wormald, N. C. (1997) 1-factorizations of random regular graphs. Random Struct. Alg. 10 305–321.3.0.CO;2-#>CrossRefGoogle Scholar
[23] Mossel, E. (2004) Survey: Information flow on trees. In Graphs, Morphisms, and Statistical Physics, Vol. 63 of DIMACS Series in Discrete Mathematics and Theoretical Computer Science, pp. 155–170.Google Scholar
[24] Mossel, E., Weitz, D. and Wormald, N. (2009) On the hardness of sampling independent sets beyond the tree threshold. Probab. Theory Rel. Fields 143 401–439.Google Scholar
[25] Restrepo, R., Shin, J., Tetali, P., Vigoda, E. and Yang, L. (2013) Improved mixing condition on the grid for counting and sampling independent sets. Probab. Theory Rel. Fields 156 75–99.Google Scholar
[26] Sinclair, A., Srivastava, P. and Thurley, M. (2014) Approximation algorithms for two-state anti-ferromagnetic spin systems on bounded degree graphs. J. Statist. Phys. 155 666–686.Google Scholar
[27] Sly, A. (2010) Computational transition at the uniqueness threshold. In Proc. 51st Annual IEEE Symposium on Foundations of Computer Science (FOCS), pp. 287–296.CrossRefGoogle Scholar
[28] Sly, A. and Sun, N. (2014) The computational hardness of counting in two-spin models on d-regular graphs. Ann. Probab. 42 2383–2416.CrossRefGoogle Scholar
[29] Talagrand, M. (2003) Spin Glasses: A Challenge for Mathematicians, Springer.Google Scholar
[30] Valiant, L. G. (1979) The complexity of enumeration and reliability problems. SIAM J. Comput. 8 410–421.CrossRefGoogle Scholar
[31] Weitz, D. (2006) Counting independent sets up to the tree threshold. In Proc. 38th Annual ACM Symposium on Theory of Computing (STOC), pp. 140–149.Google Scholar
[32] Wormald, N. C. (1999) Models of random regular graphs. In Surveys in Combinatorics 1999 (Lamb, J. D. and Preece, D. A., eds), Cambridge University Press, pp. 239–298.CrossRefGoogle Scholar
[33] Zhang, J., Liang, H. and Bai, F. (2011) Approximating partition functions of two-state spin systems. Inform. Process. Lett. 111 702–710.Google Scholar