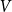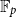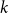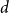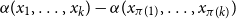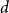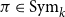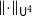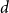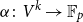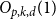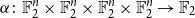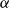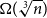1. Introduction
For a function
![]() $f \colon G \to \mathbb{C}$
on a finite abelian group
$f \colon G \to \mathbb{C}$
on a finite abelian group
![]() $G$
, the Gowers uniformity norms
$G$
, the Gowers uniformity norms
![]() $\|\!\cdot\! \|_{\mathsf{U}^k}$
, introduced by Gowers in [Reference Gowers6] are given by the formula
$\|\!\cdot\! \|_{\mathsf{U}^k}$
, introduced by Gowers in [Reference Gowers6] are given by the formula
where
![]() $\Delta \kern -7.5pt\mbox{$\huge \kern0.9pt\raise 0.2ex\hbox{.}$}_{\,\,a}$
stands for the discrete multiplicative derivative operator defined by
$\Delta \kern -7.5pt\mbox{$\huge \kern0.9pt\raise 0.2ex\hbox{.}$}_{\,\,a}$
stands for the discrete multiplicative derivative operator defined by
![]() $\Delta \kern -7.5pt\mbox{$\huge \kern0.9pt\raise 0.2ex\hbox{.}$}_{\,\,a} f(x) = f(x + a) \overline{f(x)}$
. Gowers introduced these norms in order to obtain a quantitative proof of Szemerédi’s theorem on arithmetic progressions, and they serve as a measure of the higher order quasirandomness of functions defined on finite abelian groups. A basic illustration of this phenomenon is given by the following fact: whenever
$\Delta \kern -7.5pt\mbox{$\huge \kern0.9pt\raise 0.2ex\hbox{.}$}_{\,\,a} f(x) = f(x + a) \overline{f(x)}$
. Gowers introduced these norms in order to obtain a quantitative proof of Szemerédi’s theorem on arithmetic progressions, and they serve as a measure of the higher order quasirandomness of functions defined on finite abelian groups. A basic illustration of this phenomenon is given by the following fact: whenever
![]() $A \subset \mathbb{Z}/N \mathbb{Z}$
is a set of size
$A \subset \mathbb{Z}/N \mathbb{Z}$
is a set of size
![]() $\delta N$
such that
$\delta N$
such that
![]() $\|{\mathbb{1}}_A - \delta \|_{\mathsf{U}^k} = o(1)$
, then
$\|{\mathbb{1}}_A - \delta \|_{\mathsf{U}^k} = o(1)$
, then
![]() $A$
has
$A$
has
![]() $(1 + o(1)) \delta ^{k+1}N^2$
arithmetic progressions of length
$(1 + o(1)) \delta ^{k+1}N^2$
arithmetic progressions of length
![]() $k + 1$
. This motivates the study of functions which have large uniformity norms. The results which describe such functions
$k + 1$
. This motivates the study of functions which have large uniformity norms. The results which describe such functions
![]() $f \colon G \to \mathbb{D} = \{z \in \mathbb{C} \colon |z| \leq 1\}$
are referred to as the inverse theorems for uniformity norms and typically have the following form: given the group
$f \colon G \to \mathbb{D} = \{z \in \mathbb{C} \colon |z| \leq 1\}$
are referred to as the inverse theorems for uniformity norms and typically have the following form: given the group
![]() $G$
and order
$G$
and order
![]() $k$
, there is some algebraically structured family of functions
$k$
, there is some algebraically structured family of functions
![]() $\mathcal{Q}$
, depending on
$\mathcal{Q}$
, depending on
![]() $G$
and
$G$
and
![]() $k$
, such that whenever
$k$
, such that whenever
![]() $f \colon G \to \mathbb{D}$
is a function with the norm bound
$f \colon G \to \mathbb{D}$
is a function with the norm bound
![]() $\|f\|_{\mathsf{U}^k} \geq c$
, then one may find an obstruction function
$\|f\|_{\mathsf{U}^k} \geq c$
, then one may find an obstruction function
![]() $q \in \mathcal{Q}$
such that
$q \in \mathcal{Q}$
such that
![]() $\Big |{\mathop{\mathbb{E}}}_{x \in G} f(x) \overline{q(x)}\Big |\geq \Omega _{c,k}(1)$
. One also requires that
$\Big |{\mathop{\mathbb{E}}}_{x \in G} f(x) \overline{q(x)}\Big |\geq \Omega _{c,k}(1)$
. One also requires that
![]() $\mathcal{Q}$
is roughly minimal in the sense that an approximate version of a converse holds; namely whenever
$\mathcal{Q}$
is roughly minimal in the sense that an approximate version of a converse holds; namely whenever
![]() $\Big |{\mathop{\mathbb{E}}}_{x \in G} f(x) \overline{q(x)}\Big |\geq c$
holds for a function
$\Big |{\mathop{\mathbb{E}}}_{x \in G} f(x) \overline{q(x)}\Big |\geq c$
holds for a function
![]() $f \colon G \to \mathbb{D}$
and obstruction
$f \colon G \to \mathbb{D}$
and obstruction
![]() $q \in \mathcal{Q}$
, then we also have the norm bound
$q \in \mathcal{Q}$
, then we also have the norm bound
![]() $\|f\|_{\mathsf{U}^k} \geq \Omega _{c, k}(1)$
.
$\|f\|_{\mathsf{U}^k} \geq \Omega _{c, k}(1)$
.
The family of obstruction functions can be taken to be nilsequences (which we will not define here) when
![]() $G = \mathbb{Z}/N\mathbb{Z}$
, as shown by Green, Tao and Ziegler [Reference Green, Tao and Ziegler5], and phases of non-classical polynomials (which we shall define later) when
$G = \mathbb{Z}/N\mathbb{Z}$
, as shown by Green, Tao and Ziegler [Reference Green, Tao and Ziegler5], and phases of non-classical polynomials (which we shall define later) when
![]() $G= \mathbb{F}_p^n$
, which follows from results of Bergelson, Tao and Ziegler [Reference Bergelson, Tao and Ziegler1] and Tao and Zielger [Reference Tao and Ziegler20]. Another approach to these questions is via theory of nilspaces developed in papers by Szegedy [Reference Szegedy19], Camarena and Szegedy [Reference Camarena and Szegedy2], and Candela, González-Sánchez and Szegedy [Reference Candela, González-Sánchez and Szegedy3]. (See also detailed treatments of this theory in [Reference Gutman, Manners and Varjú9, Reference Gutman, Manners and Varjú10, Reference Gutman, Manners and Varjú11].)
$G= \mathbb{F}_p^n$
, which follows from results of Bergelson, Tao and Ziegler [Reference Bergelson, Tao and Ziegler1] and Tao and Zielger [Reference Tao and Ziegler20]. Another approach to these questions is via theory of nilspaces developed in papers by Szegedy [Reference Szegedy19], Camarena and Szegedy [Reference Camarena and Szegedy2], and Candela, González-Sánchez and Szegedy [Reference Candela, González-Sánchez and Szegedy3]. (See also detailed treatments of this theory in [Reference Gutman, Manners and Varjú9, Reference Gutman, Manners and Varjú10, Reference Gutman, Manners and Varjú11].)
The inverse theorems mentioned above are either ineffective or give poor bounds and, given the applications, it is of interest to make the proofs quantitative. For general
![]() $k$
, this was achieved by Manners [Reference Manners14] for the case when
$k$
, this was achieved by Manners [Reference Manners14] for the case when
![]() $G = \mathbb{Z}/N\mathbb{Z}$
and by Gowers and the author in [Reference Gowers and Milićević8] for the case when
$G = \mathbb{Z}/N\mathbb{Z}$
and by Gowers and the author in [Reference Gowers and Milićević8] for the case when
![]() $G = \mathbb{F}_p^n$
, provided
$G = \mathbb{F}_p^n$
, provided
![]() $p \geq k$
, which is known as the high-characteristic case, when the family of obstruction functions reduces to polynomials in the usual sense. Previously, quantitative bounds were obtained in the inverse question for
$p \geq k$
, which is known as the high-characteristic case, when the family of obstruction functions reduces to polynomials in the usual sense. Previously, quantitative bounds were obtained in the inverse question for
![]() $\|\!\cdot\! \|_{\mathsf{U}^3}$
norm by Green and Tao [Reference Green and Tao4] for abelian groups of odd order and by Samorodnitsky when
$\|\!\cdot\! \|_{\mathsf{U}^3}$
norm by Green and Tao [Reference Green and Tao4] for abelian groups of odd order and by Samorodnitsky when
![]() $G = \mathbb{F}_2^n$
in [Reference Samorodnitsky18] (see also a very recent work of Jamneshan and Tao [Reference Jamneshan and Tao12]).
$G = \mathbb{F}_2^n$
in [Reference Samorodnitsky18] (see also a very recent work of Jamneshan and Tao [Reference Jamneshan and Tao12]).
On the other hand, in the so-called low characteristic case, where
![]() $p \lt k$
, the bounds are still ineffective. However, even in that case [Reference Gowers and Milićević8] gives a strong partial result. In the theorem below
$p \lt k$
, the bounds are still ineffective. However, even in that case [Reference Gowers and Milićević8] gives a strong partial result. In the theorem below
![]() $\omega = \exp (2 \pi i/ p)$
.
$\omega = \exp (2 \pi i/ p)$
.
Theorem 1. (Gowers and Milićević [Reference Gowers and Milićević8]). Suppose that
![]() $f \colon \mathbb{F}^n_p \to \mathbb{D}$
is a function such that
$f \colon \mathbb{F}^n_p \to \mathbb{D}$
is a function such that
![]() $\|f\|_{\mathsf{U}^{k}} \geq c$
. Then there exists a multilinear form
$\|f\|_{\mathsf{U}^{k}} \geq c$
. Then there exists a multilinear form
![]() $\alpha \colon \underbrace{\mathbb{F}^n_p \times \mathbb{F}^n_p \times \ldots \times \mathbb{F}^n_p}_{k-1} \to \mathbb{F}_p$
such that
$\alpha \colon \underbrace{\mathbb{F}^n_p \times \mathbb{F}^n_p \times \ldots \times \mathbb{F}^n_p}_{k-1} \to \mathbb{F}_p$
such that
From now on, we focus on
![]() $G = \mathbb{F}_p^n$
in the rest of the introduction. Before proceeding with the discussion, we need to recall the notion of the partition rank of a multilinear form introduced by Naslund in [Reference Naslund17]. It is defined to be the least number
$G = \mathbb{F}_p^n$
in the rest of the introduction. Before proceeding with the discussion, we need to recall the notion of the partition rank of a multilinear form introduced by Naslund in [Reference Naslund17]. It is defined to be the least number
![]() $m$
such that a multilinear form
$m$
such that a multilinear form
![]() $\alpha \colon G^d \to \mathbb{F}_p$
can be expressed as
$\alpha \colon G^d \to \mathbb{F}_p$
can be expressed as
where
![]() $\beta _i \colon G^{I_i} \to \mathbb{F}_p$
and
$\beta _i \colon G^{I_i} \to \mathbb{F}_p$
and
![]() $\gamma _i \colon G^{[d] \setminus I_i} \to \mathbb{F}_p$
are multilinear maps for
$\gamma _i \colon G^{[d] \setminus I_i} \to \mathbb{F}_p$
are multilinear maps for
![]() $i \in [m]$
. We denote the quantity
$i \in [m]$
. We denote the quantity
![]() $m$
by
$m$
by
![]() $\textrm{prank}(\alpha )$
. We may think of partition rank as a measure of distance between two multilinear forms; the smaller the partition rank of their difference is, the closer they are. As an illustration of this principle in the context of Theorem 1, we have the following lemma.
$\textrm{prank}(\alpha )$
. We may think of partition rank as a measure of distance between two multilinear forms; the smaller the partition rank of their difference is, the closer they are. As an illustration of this principle in the context of Theorem 1, we have the following lemma.
Lemma 2.
Suppose that a function
![]() $f \colon G \to \mathbb{D}$
and a multilinear form
$f \colon G \to \mathbb{D}$
and a multilinear form
![]() $\alpha \colon G^{k-1} \to \mathbb{F}_p$
satisfy
$\alpha \colon G^{k-1} \to \mathbb{F}_p$
satisfy
Let
![]() $\beta \colon G^{k-1} \to \mathbb{F}_p$
be another multilinear form such that
$\beta \colon G^{k-1} \to \mathbb{F}_p$
be another multilinear form such that
![]() ${prank}(\alpha - \beta ) \leq r$
. Then
${prank}(\alpha - \beta ) \leq r$
. Then
Returning to the discussion of the inverse theorems for uniformity norms in finite vector spaces, the deduction of the inverse theorem when
![]() $p \geq k$
proceeds by studying the multilinear form
$p \geq k$
proceeds by studying the multilinear form
![]() $\alpha$
provided by the Theorem 1. The symmetry argument of Green and Tao [Reference Green and Tao4] and the good bounds for the analytic versus partition rank problem [Reference Janzer13, Reference Milićević15] show that
$\alpha$
provided by the Theorem 1. The symmetry argument of Green and Tao [Reference Green and Tao4] and the good bounds for the analytic versus partition rank problem [Reference Janzer13, Reference Milićević15] show that
![]() $\alpha$
is
$\alpha$
is
![]() $r$
-approximately symmetric for some
$r$
-approximately symmetric for some
![]() $r = \exp ^{(O_k(1))}(O_{k,p}(c^{-1}))$
, by which we mean that the partition rank of the multilinear form
$r = \exp ^{(O_k(1))}(O_{k,p}(c^{-1}))$
, by which we mean that the partition rank of the multilinear form
![]() $(x_1, \ldots, x_{k-1}) \mapsto \alpha (x_1, \ldots, x_{k-1}) - \alpha (x_{\pi (1)}, \ldots, x_{\pi (k-1)})$
is at most
$(x_1, \ldots, x_{k-1}) \mapsto \alpha (x_1, \ldots, x_{k-1}) - \alpha (x_{\pi (1)}, \ldots, x_{\pi (k-1)})$
is at most
![]() $r$
for all
$r$
for all
![]() $\pi \in \textrm{Sym}_{k-1}$
. To finish the proof of the inverse theorem, at the very last step we invoke the assumption
$\pi \in \textrm{Sym}_{k-1}$
. To finish the proof of the inverse theorem, at the very last step we invoke the assumption
![]() $p \geq k$
, which allows us to define the symmetric multilinear map
$p \geq k$
, which allows us to define the symmetric multilinear map
![]() $\sigma \colon G^{k-1} \to \mathbb{F}_p$
by
$\sigma \colon G^{k-1} \to \mathbb{F}_p$
by
which satisfies
![]() $\textrm{prank} (\sigma - \alpha ) \leq (k-1)! r$
since
$\textrm{prank} (\sigma - \alpha ) \leq (k-1)! r$
since
![]() $\alpha$
is
$\alpha$
is
![]() $r$
-approximately symmetric. Lemma 2 allows us to replace
$r$
-approximately symmetric. Lemma 2 allows us to replace
![]() $\alpha$
by
$\alpha$
by
![]() $\sigma$
. As it turns out, when
$\sigma$
. As it turns out, when
![]() $p \geq k$
the polarization identity shows that all symmetric forms are iterated discrete additive derivatives of polynomials (see the definition of non-classical polynomials below for the definition of discrete additive derivatives), showing that the function
$p \geq k$
the polarization identity shows that all symmetric forms are iterated discrete additive derivatives of polynomials (see the definition of non-classical polynomials below for the definition of discrete additive derivatives), showing that the function
![]() $x \mapsto f(x) \omega ^{\alpha (x,\ldots, x)}$
has large
$x \mapsto f(x) \omega ^{\alpha (x,\ldots, x)}$
has large
![]() $\|\!\cdot\! \|_{\mathsf{U}^{k-1}}$
norm, which completes the proof (we assume the inverse theorem for the
$\|\!\cdot\! \|_{\mathsf{U}^{k-1}}$
norm, which completes the proof (we assume the inverse theorem for the
![]() $\|\!\cdot\! \|_{\mathsf{U}^{k-1}}$
norm as inductive hypothesis).
$\|\!\cdot\! \|_{\mathsf{U}^{k-1}}$
norm as inductive hypothesis).
Low characteristic obstacles
Let us now define non-classical polynomials which are the relevant obstructions in the low characteristic case. Similarly to discrete multiplicative derivative, for
![]() $a \in G$
we define discrete additive derivative operator
$a \in G$
we define discrete additive derivative operator
![]() $\Delta _a$
by expression
$\Delta _a$
by expression
![]() $\Delta _a f(x) = f(x + a) - f(x)$
for a function
$\Delta _a f(x) = f(x + a) - f(x)$
for a function
![]() $f \colon G \to H$
from
$f \colon G \to H$
from
![]() $G$
to another abelian group
$G$
to another abelian group
![]() $H$
. A function
$H$
. A function
![]() $f \colon \mathbb{F}_p^n \to \mathbb{T} = \mathbb{R}/\mathbb{Z}$
is a non-classical polynomial of degree at most
$f \colon \mathbb{F}_p^n \to \mathbb{T} = \mathbb{R}/\mathbb{Z}$
is a non-classical polynomial of degree at most
![]() $d$
if
$d$
if
![]() $\Delta _{a_1} \ldots \Delta _{a_{d+1}} f(x) = 0$
for all
$\Delta _{a_1} \ldots \Delta _{a_{d+1}} f(x) = 0$
for all
![]() $a_1, \ldots, a_{d+1}, x \in \mathbb{F}_p^n$
. (See [Reference Tao and Ziegler20] for further details, including alternative description of non-classical polynomials.)
$a_1, \ldots, a_{d+1}, x \in \mathbb{F}_p^n$
. (See [Reference Tao and Ziegler20] for further details, including alternative description of non-classical polynomials.)
The first obvious question is, given that the family of obstruction functions is richer when
![]() $p \lt k$
due to emergence of non-classical polynomials, how could we get from multilinear forms in (1) to a non-classical polynomial? It turns out that, as in the case of classical polynomials, the iterated discrete additive derivative of a non-classical polynomial (applied the right number of times) is a symmetric multilinear form and it is possible to give characterizations of the forms that arise in this way. The following lemma of Tidor [Reference Tidor21], building upon earlier work of Tao and Ziegler, achieves this goal.
$p \lt k$
due to emergence of non-classical polynomials, how could we get from multilinear forms in (1) to a non-classical polynomial? It turns out that, as in the case of classical polynomials, the iterated discrete additive derivative of a non-classical polynomial (applied the right number of times) is a symmetric multilinear form and it is possible to give characterizations of the forms that arise in this way. The following lemma of Tidor [Reference Tidor21], building upon earlier work of Tao and Ziegler, achieves this goal.
Lemma 3. (Tidor [Reference Tidor21]). Let
![]() $\alpha \colon G^{k-1} \to \mathbb{F}_p$
be a multilinear form. Then
$\alpha \colon G^{k-1} \to \mathbb{F}_p$
be a multilinear form. Then
![]() $\alpha$
is the discrete additive derivative of order
$\alpha$
is the discrete additive derivative of order
![]() $k-1$
of a non-classical polynomial of degree
$k-1$
of a non-classical polynomial of degree
![]() $k-1$
if and only if
$k-1$
if and only if
![]() $\alpha$
is symmetric and
$\alpha$
is symmetric and
holds for all
![]() $x,y,a_{p+2},\ldots a_{k-1} \in G$
.
$x,y,a_{p+2},\ldots a_{k-1} \in G$
.
We say that a multilinear form is strongly symmetric if it is symmetric and obeys the additional condition (2), as in the lemma above. Therefore, we may again pass from a multilinear form
![]() $\alpha$
to the desired obstruction, provided we can show some additional properties of
$\alpha$
to the desired obstruction, provided we can show some additional properties of
![]() $\alpha$
.
$\alpha$
.
In fact, in his work on the inverse question for
![]() $\|\!\cdot\! \|_{\mathsf{U}^4}$
norm in the case of low characteristic [Reference Tidor21], Tidor first showed that one may assume that
$\|\!\cdot\! \|_{\mathsf{U}^4}$
norm in the case of low characteristic [Reference Tidor21], Tidor first showed that one may assume that
![]() $\alpha$
is symmetric and then used that information to prove strong symmetry. Given all this, Tidor formulated the following conjecture, which he proved for the case of trilinear maps.
$\alpha$
is symmetric and then used that information to prove strong symmetry. Given all this, Tidor formulated the following conjecture, which he proved for the case of trilinear maps.
Conjecture 4. (Tidor [Reference Tidor21]). Let
![]() $\alpha \colon G^k \to \mathbb{F}_p$
be an
$\alpha \colon G^k \to \mathbb{F}_p$
be an
![]() $r$
-approximately symmetric multilinear form. Then there exists a symmetric multilinear form
$r$
-approximately symmetric multilinear form. Then there exists a symmetric multilinear form
![]() $\sigma \colon G^k \to \mathbb{F}_p$
such that
$\sigma \colon G^k \to \mathbb{F}_p$
such that
![]() $\textrm{prank}(\sigma - \alpha ) \leq O(r^{O(1)})$
(where the implicit constants may depend on
$\textrm{prank}(\sigma - \alpha ) \leq O(r^{O(1)})$
(where the implicit constants may depend on
![]() $p$
and
$p$
and
![]() $k$
).
$k$
).
The main result of this paper is that, despite its formulation being rather natural, the conjecture above is false.
Theorem 5.
Given a sufficiently large positive integer
![]() $n$
there exists a multilinear form
$n$
there exists a multilinear form
![]() $\alpha \colon \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \to \mathbb{F}_2$
which is 3-approximately symmetric and
$\alpha \colon \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \to \mathbb{F}_2$
which is 3-approximately symmetric and
![]() ${prank}(\sigma - \alpha ) \geq \Omega (\sqrt [3]{n})$
for all symmetric multilinear forms
${prank}(\sigma - \alpha ) \geq \Omega (\sqrt [3]{n})$
for all symmetric multilinear forms
![]() $\sigma$
.
$\sigma$
.
Regarding the approach to a quantitative inverse theorem for uniformity norms in the case of low characteristic, this means that one needs to work more closely with the assumption (1). In fact, it is possible to overcome the additional difficulties identified in this paper, and to prove a quantitative inverse theorem for uniformity norms
![]() $\mathsf{U}^5$
and
$\mathsf{U}^5$
and
![]() $\mathsf{U}^6$
in the case of low characteristic.
$\mathsf{U}^6$
in the case of low characteristic.
Theorem 6. (Quantitative inverse theorem for
![]() $\mathsf{U}^5$
and
$\mathsf{U}^5$
and
![]() $\mathsf{U}^6$
norms, Corollary 6 in [Reference Milićević16]). Let
$\mathsf{U}^6$
norms, Corollary 6 in [Reference Milićević16]). Let
![]() $k \in \{5,6\}$
. Suppose that
$k \in \{5,6\}$
. Suppose that
![]() $f \colon \mathbb{F}^n_2 \to \mathbb{D}$
is a function such that
$f \colon \mathbb{F}^n_2 \to \mathbb{D}$
is a function such that
![]() $\|f\|_{\mathsf{U}^{k}} \geq c$
. Then there exists a non-classical polynomial
$\|f\|_{\mathsf{U}^{k}} \geq c$
. Then there exists a non-classical polynomial
![]() $q \colon \mathbb{F}_2^n \to \mathbb{T}$
of degree at most
$q \colon \mathbb{F}_2^n \to \mathbb{T}$
of degree at most
![]() $k-1$
such that
$k-1$
such that
Counterexample overview
The multilinear form
![]() $\alpha \colon \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \to \mathbb{F}_2$
that will serve us as a counterexample will have the crucial properties that it is symmetric in the first three variables, while satisfying the identity
$\alpha \colon \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \to \mathbb{F}_2$
that will serve us as a counterexample will have the crucial properties that it is symmetric in the first three variables, while satisfying the identity
for some bilinear map
![]() $\rho$
of high rank.Footnote
1
It is easy to see that such a form
$\rho$
of high rank.Footnote
1
It is easy to see that such a form
![]() $\alpha$
is necessarily 3-approximately symmetric. On the other hand, to prove that
$\alpha$
is necessarily 3-approximately symmetric. On the other hand, to prove that
![]() $\alpha$
is far from symmetric multilinear forms we use bilinear regularity method, used in [Reference Gowers and Milićević7], which consists of passing to subspaces where the rank of bilinear maps is large and then relying on the high-rank property to obtain equidistribution of values of the relevant bilinear maps. Using the usual graph-theoretic regularity methodFootnote
2
would give much worse bounds in Theorem 5.
$\alpha$
is far from symmetric multilinear forms we use bilinear regularity method, used in [Reference Gowers and Milićević7], which consists of passing to subspaces where the rank of bilinear maps is large and then relying on the high-rank property to obtain equidistribution of values of the relevant bilinear maps. Using the usual graph-theoretic regularity methodFootnote
2
would give much worse bounds in Theorem 5.
2. Preliminaries
For the rest of the paper, fix a positive integer
![]() $n$
and set
$n$
and set
![]() $G = \mathbb{F}_2^n$
. In this preliminary section we setup the notation for an action of the symmetry group
$G = \mathbb{F}_2^n$
. In this preliminary section we setup the notation for an action of the symmetry group
![]() $\textrm{Sym}_4$
on
$\textrm{Sym}_4$
on
![]() $G^4$
, we recall the notion and properties of the rank of bilinear maps and we discuss the bilinear regularity method needed for the proof of Theorem 5.
$G^4$
, we recall the notion and properties of the rank of bilinear maps and we discuss the bilinear regularity method needed for the proof of Theorem 5.
Action of
 $\textrm{Sym}_4$
$\textrm{Sym}_4$
We define a natural action of
![]() $\textrm{Sym}_4$
on
$\textrm{Sym}_4$
on
![]() $G^4$
given by permuting the coordinates, which is similar to the left regular representation of the group
$G^4$
given by permuting the coordinates, which is similar to the left regular representation of the group
![]() $\textrm{Sym}_4$
. For a permutation
$\textrm{Sym}_4$
. For a permutation
![]() $\pi \in \textrm{Sym}_4$
we misuse the notation and write
$\pi \in \textrm{Sym}_4$
we misuse the notation and write
![]() $\pi \colon G^4 \to G^4$
for the map defined by
$\pi \colon G^4 \to G^4$
for the map defined by
![]() $\pi (x_1, x_2, x_3, x_4) = (x_{\pi ^{-1}(1)},$
$\pi (x_1, x_2, x_3, x_4) = (x_{\pi ^{-1}(1)},$
![]() $x_{\pi ^{-1}(2)},$
$x_{\pi ^{-1}(2)},$
![]() $x_{\pi ^{-1}(3)},$
$x_{\pi ^{-1}(3)},$
![]() $x_{\pi ^{-1}(4)})$
. It is easy to see that this defines an action on
$x_{\pi ^{-1}(4)})$
. It is easy to see that this defines an action on
![]() $G^4$
. Hence, given a multilinear form
$G^4$
. Hence, given a multilinear form
![]() $\alpha \colon G^4 \to \mathbb{F}_2$
and a permutation
$\alpha \colon G^4 \to \mathbb{F}_2$
and a permutation
![]() $\pi$
inducing the map
$\pi$
inducing the map
![]() $\pi \colon G^4 \to G^4$
, we may compose the two maps and the composition
$\pi \colon G^4 \to G^4$
, we may compose the two maps and the composition
![]() $\alpha \circ \pi$
would also be a multilinear form. For example if
$\alpha \circ \pi$
would also be a multilinear form. For example if
![]() $\pi = (1\,\,2\,\,3)$
in the cycle notation, then
$\pi = (1\,\,2\,\,3)$
in the cycle notation, then
![]() $\alpha \circ \pi (x_1, x_2, x_3, x_4) = \alpha (x_3, x_1, x_2, x_4)$
. With this notation, our main result can be expressed as follows: there exists a multilinear form
$\alpha \circ \pi (x_1, x_2, x_3, x_4) = \alpha (x_3, x_1, x_2, x_4)$
. With this notation, our main result can be expressed as follows: there exists a multilinear form
![]() $\alpha \colon G^4 \to \mathbb{F}_2$
such that
$\alpha \colon G^4 \to \mathbb{F}_2$
such that
![]() $\alpha + \alpha \circ \pi$
is of low partition rank for all
$\alpha + \alpha \circ \pi$
is of low partition rank for all
![]() $\pi \in \textrm{Sym}_4$
and
$\pi \in \textrm{Sym}_4$
and
![]() $\alpha$
differs from any symmetric multilinear form by a multilinear form of large partition rank.
$\alpha$
differs from any symmetric multilinear form by a multilinear form of large partition rank.
Rank of bilinear maps
Let
![]() $U, V$
be finite-dimensional vector spaces over
$U, V$
be finite-dimensional vector spaces over
![]() $\mathbb{F}_2$
. Let
$\mathbb{F}_2$
. Let
![]() $\beta \colon U \times V \to \mathbb{F}_2$
be a bilinear form. Fix a scalar product on
$\beta \colon U \times V \to \mathbb{F}_2$
be a bilinear form. Fix a scalar product on
![]() $V$
and let
$V$
and let
![]() $B \colon U \to V$
be the map such that
$B \colon U \to V$
be the map such that
![]() $\beta (x,y) = B(x) \cdot y$
for all
$\beta (x,y) = B(x) \cdot y$
for all
![]() $x \in U$
and
$x \in U$
and
![]() $y \in V$
. We define the rank of
$y \in V$
. We define the rank of
![]() $\beta$
to be the rank of
$\beta$
to be the rank of
![]() $B$
. The following lemma gives a few other characterizations of the rank and shows that the rank is well-defined (this follows from part (i)).
$B$
. The following lemma gives a few other characterizations of the rank and shows that the rank is well-defined (this follows from part (i)).
Lemma 7. (Alternative characterizations of rank). Let
![]() $\beta \colon U \times V \to \mathbb{F}_2$
be a bilinear form.
$\beta \colon U \times V \to \mathbb{F}_2$
be a bilinear form.
-
i. We have
 ${\mathop{\mathbb{E}}}_{x \in U,y \in V} (\!-\!1)^{\beta (x,y)} = 2^{-\textrm{rank} \beta }$
.
${\mathop{\mathbb{E}}}_{x \in U,y \in V} (\!-\!1)^{\beta (x,y)} = 2^{-\textrm{rank} \beta }$
. -
ii. Whenever
 $\beta (x,y) = \sum _{i \in [s]} u_i(x) v_i(y)$
for linear forms
$\beta (x,y) = \sum _{i \in [s]} u_i(x) v_i(y)$
for linear forms
 $u_1, \ldots, u_s \colon U \to \mathbb{F}_2$
and
$u_1, \ldots, u_s \colon U \to \mathbb{F}_2$
and
 $v_1, \ldots, v_s \colon V \to \mathbb{F}_2$
such that
$v_1, \ldots, v_s \colon V \to \mathbb{F}_2$
such that
 $u_1, \ldots, u_s$
are linearly independent and
$u_1, \ldots, u_s$
are linearly independent and
 $v_1, \ldots, v_s$
are linearly independent, then
$v_1, \ldots, v_s$
are linearly independent, then
 $s = \textrm{rank} \beta$
.
$s = \textrm{rank} \beta$
. -
iii. The rank of
 $\beta$
is the least number
$\beta$
is the least number
 $s$
such that
$s$
such that
 $\beta (x,y) = \sum _{i \in [s]} u_i(x) v_i(y)$
for linear forms
$\beta (x,y) = \sum _{i \in [s]} u_i(x) v_i(y)$
for linear forms
 $u_1, \ldots, u_s \colon U \to \mathbb{F}_2$
and
$u_1, \ldots, u_s \colon U \to \mathbb{F}_2$
and
 $v_1, \ldots, v_s \colon V \to \mathbb{F}_2$
.
$v_1, \ldots, v_s \colon V \to \mathbb{F}_2$
.
Proof.
Proof of (i). If
![]() $\beta (x,y) = B(x) \cdot y$
for all
$\beta (x,y) = B(x) \cdot y$
for all
![]() $x \in U, y \in V$
, then
$x \in U, y \in V$
, then
By the rank-nullity theorem
![]() $|\ker B|/|U| = 1/|\textrm{Im} B|$
. The rank of
$|\ker B|/|U| = 1/|\textrm{Im} B|$
. The rank of
![]() $\beta$
is defined as the dimension of the image space
$\beta$
is defined as the dimension of the image space
![]() $\textrm{Im} B$
, hence
$\textrm{Im} B$
, hence
as desired.
Proof of (ii). Let us define linear map
![]() $u \colon U \to \mathbb{F}_2^s$
by concatenating forms
$u \colon U \to \mathbb{F}_2^s$
by concatenating forms
![]() $u_i$
, namely
$u_i$
, namely
![]() $u = (u_1, \ldots, u_s)$
. We claim that
$u = (u_1, \ldots, u_s)$
. We claim that
![]() $u$
is surjective. If it was not surjective, the subspace
$u$
is surjective. If it was not surjective, the subspace
![]() $\textrm{Im} u \leq \mathbb{F}_2^s$
would be proper and there would exist a non-zero vector
$\textrm{Im} u \leq \mathbb{F}_2^s$
would be proper and there would exist a non-zero vector
![]() $\lambda \in (\textrm{Im} u)^\perp$
. But then
$\lambda \in (\textrm{Im} u)^\perp$
. But then
![]() $\lambda _1 u_1 + \ldots + \lambda _s u_s$
would be identically zero, which would be in contradiction with the assumption that
$\lambda _1 u_1 + \ldots + \lambda _s u_s$
would be identically zero, which would be in contradiction with the assumption that
![]() $u_1, \ldots, u_s$
are independent. In particular, the linear map
$u_1, \ldots, u_s$
are independent. In particular, the linear map
![]() $u \colon U \to \mathbb{F}_2^s$
takes all values in
$u \colon U \to \mathbb{F}_2^s$
takes all values in
![]() $\mathbb{F}_2^s$
an equal number of times (namely
$\mathbb{F}_2^s$
an equal number of times (namely
![]() $|\ker u| = 2^{-s}|U|$
times). Using the same property for
$|\ker u| = 2^{-s}|U|$
times). Using the same property for
![]() $v_1, \ldots, v_s$
and claim (i) of the lemma we conclude that
$v_1, \ldots, v_s$
and claim (i) of the lemma we conclude that
proving that
![]() $s = \textrm{rank} \beta$
.
$s = \textrm{rank} \beta$
.
Proof of (iii). Let
![]() $d = \dim U$
. Clearly, such a decomposition exists, as we may simply take a basis
$d = \dim U$
. Clearly, such a decomposition exists, as we may simply take a basis
![]() $e_1, \ldots, e_d$
of
$e_1, \ldots, e_d$
of
![]() $U$
, giving coordinates
$U$
, giving coordinates
![]() $x_1, \ldots, x_d$
of vectors
$x_1, \ldots, x_d$
of vectors
![]() $x \in U$
, and consider
$x \in U$
, and consider
On the other hand, if we have a decomposition with smallest possible
![]() $s$
then
$s$
then
![]() $u_1, \ldots, u_s$
need to be linearly independent. To see that, note that if have linear dependence, then (after a possible reordering of the forms) we have
$u_1, \ldots, u_s$
need to be linearly independent. To see that, note that if have linear dependence, then (after a possible reordering of the forms) we have
![]() $u_1 = \sum _{j \in [2,s]} \mu _j u_j$
, so
$u_1 = \sum _{j \in [2,s]} \mu _j u_j$
, so
which has
![]() $s-1$
terms in the sum, which is a contradiction. Hence
$s-1$
terms in the sum, which is a contradiction. Hence
![]() $u_1, \ldots, u_s$
are linearly independent, and analogously, so are
$u_1, \ldots, u_s$
are linearly independent, and analogously, so are
![]() $v_1, \ldots, v_s$
. The claim follows from the part (ii).
$v_1, \ldots, v_s$
. The claim follows from the part (ii).
Let us also record two very simple but useful facts about bilinear forms of low rank.
Lemma 8.
Let
![]() $\beta \colon U \times V \to \mathbb{F}_2$
be a bilinear form of rank
$\beta \colon U \times V \to \mathbb{F}_2$
be a bilinear form of rank
![]() $r$
. Then there exists a subspace
$r$
. Then there exists a subspace
![]() $U' \leq U$
of codimension at most
$U' \leq U$
of codimension at most
![]() $r$
in
$r$
in
![]() $U$
such that
$U$
such that
![]() $\beta |_{U' \times V} = 0$
.
$\beta |_{U' \times V} = 0$
.
Proof. By the definition of rank,
![]() $r$
is the rank of the linear map
$r$
is the rank of the linear map
![]() $B \colon U \to V$
that satisfies
$B \colon U \to V$
that satisfies
![]() $\beta (x,y) = B(x) \cdot y$
for all
$\beta (x,y) = B(x) \cdot y$
for all
![]() $x \in U, y \in V$
for a given scalar product on
$x \in U, y \in V$
for a given scalar product on
![]() $V$
. By the rank-nullity theorem, the kernel
$V$
. By the rank-nullity theorem, the kernel
![]() $U' = \textrm{ker} B \leq U$
has codimension
$U' = \textrm{ker} B \leq U$
has codimension
![]() $r$
. Hence, when
$r$
. Hence, when
![]() $x \in U', y \in V$
we have
$x \in U', y \in V$
we have
![]() $\beta (x,y) = B(x) \cdot y = 0$
, as desired.
$\beta (x,y) = B(x) \cdot y = 0$
, as desired.
Lemma 9.
Let
![]() $\beta \colon U \times V \to \mathbb{F}_2$
be a bilinear form of rank
$\beta \colon U \times V \to \mathbb{F}_2$
be a bilinear form of rank
![]() $r$
. Let
$r$
. Let
![]() $U' \leq U$
be a subspace of codimension
$U' \leq U$
be a subspace of codimension
![]() $d$
inside
$d$
inside
![]() $U$
. Then
$U$
. Then
![]() $\beta |_{U' \times V}$
has rank at least
$\beta |_{U' \times V}$
has rank at least
![]() $r -d$
.
$r -d$
.
Proof. Let
![]() $s$
be the rank of
$s$
be the rank of
![]() $\beta |_{U' \times V}$
. By part (iii) of Lemma 7 we have linear forms
$\beta |_{U' \times V}$
. By part (iii) of Lemma 7 we have linear forms
![]() $u_1, \ldots, u_s \colon U' \to \mathbb{F}_2$
and
$u_1, \ldots, u_s \colon U' \to \mathbb{F}_2$
and
![]() $v_1, \ldots, v_s \colon V \to \mathbb{F}_2$
such that
$v_1, \ldots, v_s \colon V \to \mathbb{F}_2$
such that
![]() $\beta (x,y) = \sum _{i \in [s]} u_i(x) v_i(y)$
holds for all
$\beta (x,y) = \sum _{i \in [s]} u_i(x) v_i(y)$
holds for all
![]() $x \in U'$
and
$x \in U'$
and
![]() $y \in V$
. We may extend each
$y \in V$
. We may extend each
![]() $u_i$
to a linear form
$u_i$
to a linear form
![]() $\tilde{u}_i \colon U \to \mathbb{F}_2$
. Let
$\tilde{u}_i \colon U \to \mathbb{F}_2$
. Let
![]() $\beta '(x,y) = \beta (x,y) + \sum _{i \in [s]} \tilde{u}_i(x) v_i(y)$
. The map
$\beta '(x,y) = \beta (x,y) + \sum _{i \in [s]} \tilde{u}_i(x) v_i(y)$
. The map
![]() $\beta '$
is a bilinear form on
$\beta '$
is a bilinear form on
![]() $U \times V$
which vanishes on
$U \times V$
which vanishes on
![]() $U' \times V$
. We claim that
$U' \times V$
. We claim that
![]() $\beta '$
has rank at most
$\beta '$
has rank at most
![]() $d$
. Since we also have that
$d$
. Since we also have that
![]() $\beta (x,y) = \beta '(x,y) + \sum _{i \in [s]} \tilde{u}_i(x) v_i(y)$
, it follows that
$\beta (x,y) = \beta '(x,y) + \sum _{i \in [s]} \tilde{u}_i(x) v_i(y)$
, it follows that
![]() $\beta$
can be written as a sum of at most
$\beta$
can be written as a sum of at most
![]() $s+d$
terms of the form
$s+d$
terms of the form
![]() $u'(x) v'(y)$
for suitable linear forms
$u'(x) v'(y)$
for suitable linear forms
![]() $u' \colon U \to \mathbb{F}_2$
and
$u' \colon U \to \mathbb{F}_2$
and
![]() $v' \colon V \to \mathbb{F}_2$
and so by part (iii) of Lemma 7 we have
$v' \colon V \to \mathbb{F}_2$
and so by part (iii) of Lemma 7 we have
![]() $r \leq s + d$
as desired. We now return to showing that
$r \leq s + d$
as desired. We now return to showing that
![]() $\textrm{rank} \beta ' \leq d$
.
$\textrm{rank} \beta ' \leq d$
.
Since
![]() $U'$
has codimension
$U'$
has codimension
![]() $d$
inside
$d$
inside
![]() $U$
, we may find linearly independent elements
$U$
, we may find linearly independent elements
![]() $e_1, \ldots, e_d \in U$
such that
$e_1, \ldots, e_d \in U$
such that
![]() $U = \langle e_1, \ldots, e_d \rangle \oplus U'$
. We thus obtain linear forms
$U = \langle e_1, \ldots, e_d \rangle \oplus U'$
. We thus obtain linear forms
![]() $\varphi _1, \ldots, \varphi _d \colon U \to \mathbb{F}_2$
and a linear map
$\varphi _1, \ldots, \varphi _d \colon U \to \mathbb{F}_2$
and a linear map
![]() $\pi \colon U \to U'$
such that for each
$\pi \colon U \to U'$
such that for each
![]() $x \in U$
we have
$x \in U$
we have
![]() $x = \sum _{i \in [d]} \varphi _i(x) e_i + \pi (x)$
. Using this decomposition, for arbitrary
$x = \sum _{i \in [d]} \varphi _i(x) e_i + \pi (x)$
. Using this decomposition, for arbitrary
![]() $x \in U, y \in V$
we see that
$x \in U, y \in V$
we see that
Part (iii) of Lemma 7 implies that
![]() $\textrm{rank}\beta ' \leq d$
.
$\textrm{rank}\beta ' \leq d$
.
Bilinear regularity method
In the proof that our example has the desired properties we need the algebraic regularity method for bilinear maps. This method was used in [Reference Gowers and Milićević7]. The following lemma, in the spirit of Corollary 5.2 of [Reference Gowers and Milićević7], essentially shows that for a given bilinear map we may pass to a subspace on which it behaves quasirandomly (which in the bilinear setting simply means that the restriction of the bilinear map has high rank).
Lemma 10. (Bilinear regularity lemma). Let
![]() $m \geq 1$
be a positive integer. Let
$m \geq 1$
be a positive integer. Let
![]() $U$
be a finite-dimensional vector space over
$U$
be a finite-dimensional vector space over
![]() $\mathbb{F}_2$
and let
$\mathbb{F}_2$
and let
![]() $\rho, \beta _1, \ldots, \beta _r \colon U \times U \to \mathbb{F}_2$
be bilinear forms such that
$\rho, \beta _1, \ldots, \beta _r \colon U \times U \to \mathbb{F}_2$
be bilinear forms such that
![]() $\textrm{rank} \rho \geq (4r + 1)m$
. Then there exist a subspace
$\textrm{rank} \rho \geq (4r + 1)m$
. Then there exist a subspace
![]() $U' \leq U$
of codimension at most
$U' \leq U$
of codimension at most
![]() $2rm$
and bilinear forms
$2rm$
and bilinear forms
![]() $\alpha _1, \ldots, \alpha _s \colon U' \times U' \to \mathbb{F}_2$
, where
$\alpha _1, \ldots, \alpha _s \colon U' \times U' \to \mathbb{F}_2$
, where
![]() $s \leq r$
, such that every non-zero linear combination of
$s \leq r$
, such that every non-zero linear combination of
![]() $\alpha _1, \ldots, \alpha _s$
and
$\alpha _1, \ldots, \alpha _s$
and
![]() $\rho |_{U' \times U'}$
has rank at least
$\rho |_{U' \times U'}$
has rank at least
![]() $m$
, while every bilinear map among
$m$
, while every bilinear map among
![]() $\beta _1, \ldots, \beta _r$
equals a linear combination of
$\beta _1, \ldots, \beta _r$
equals a linear combination of
![]() $\alpha _1, \ldots, \alpha _s$
and
$\alpha _1, \ldots, \alpha _s$
and
![]() $\rho$
on
$\rho$
on
![]() $U' \times U'$
.
$U' \times U'$
.
Proof. Let us first set
![]() $s = r$
,
$s = r$
,
![]() $U' = U$
and
$U' = U$
and
![]() $\alpha _i = \beta _i$
. We shall modify the number
$\alpha _i = \beta _i$
. We shall modify the number
![]() $s$
, subspace
$s$
, subspace
![]() $U'$
and maps
$U'$
and maps
![]() $\alpha _1, \ldots, \alpha _s$
throughout the proof. At each step of the proof the number of forms
$\alpha _1, \ldots, \alpha _s$
throughout the proof. At each step of the proof the number of forms
![]() $s$
will decrease by 1, while the codimension of
$s$
will decrease by 1, while the codimension of
![]() $U'$
will increase by at most
$U'$
will increase by at most
![]() $2m$
. Note that every bilinear map among
$2m$
. Note that every bilinear map among
![]() $\beta _1, \ldots, \beta _r$
equals some
$\beta _1, \ldots, \beta _r$
equals some
![]() $\alpha _i$
on
$\alpha _i$
on
![]() $U' \times U'$
so we just need to make sure that ranks of all non-zero linear combinations of
$U' \times U'$
so we just need to make sure that ranks of all non-zero linear combinations of
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\rho$
are sufficiently large. Suppose on the contrary that there is a linear combination of maps
$\rho$
are sufficiently large. Suppose on the contrary that there is a linear combination of maps
![]() $\alpha _1, \ldots, \alpha _s$
and
$\alpha _1, \ldots, \alpha _s$
and
![]() $\rho |_{U' \times U'}$
such that
$\rho |_{U' \times U'}$
such that
Since by Lemma 9 we have
![]() $\textrm{rank} \rho |_{U' \times U'} \geq \textrm{rank} \rho - 2(\dim U - \dim U') \geq m$
, there exists a non-zero
$\textrm{rank} \rho |_{U' \times U'} \geq \textrm{rank} \rho - 2(\dim U - \dim U') \geq m$
, there exists a non-zero
![]() $\lambda _j$
. Reordering
$\lambda _j$
. Reordering
![]() $\alpha _i$
if necessary, we may assume that
$\alpha _i$
if necessary, we may assume that
![]() $\lambda _s = 1$
. Thus, by Lemma 7
(iii) there exist linear forms
$\lambda _s = 1$
. Thus, by Lemma 7
(iii) there exist linear forms
![]() $v_1, \ldots, v_m, v'_1, \ldots, v'_m \colon U' \to \mathbb{F}_2$
such that
$v_1, \ldots, v_m, v'_1, \ldots, v'_m \colon U' \to \mathbb{F}_2$
such that
We may replace
![]() $U'$
by
$U'$
by
![]() $U' \cap \{x \in U' \colon (\forall i \in [m]) v_i(x) = v'_i(x) = 0\}$
and remove the form
$U' \cap \{x \in U' \colon (\forall i \in [m]) v_i(x) = v'_i(x) = 0\}$
and remove the form
![]() $\alpha _s$
from the sequence. The property that every bilinear map among
$\alpha _s$
from the sequence. The property that every bilinear map among
![]() $\beta _1, \ldots, \beta _r$
equals a suitable linear combination on
$\beta _1, \ldots, \beta _r$
equals a suitable linear combination on
![]() $U' \times U'$
is preserved and the procedure must terminate after at most
$U' \times U'$
is preserved and the procedure must terminate after at most
![]() $r$
steps.
$r$
steps.
The next lemma is an algebraic counting lemma, similar to Lemma 5.3 of [Reference Gowers and Milićević7].
Lemma 11. (Bilinear counting lemma). Suppose that
![]() $\alpha \colon \mathbb{F}_2^n \times \mathbb{F}_2^n \to \mathbb{F}_2^r$
is a bilinear map with the property that the form
$\alpha \colon \mathbb{F}_2^n \times \mathbb{F}_2^n \to \mathbb{F}_2^r$
is a bilinear map with the property that the form
![]() $\lambda \cdot \alpha$
has rank at least
$\lambda \cdot \alpha$
has rank at least
![]() $m$
for all non-zero vectors
$m$
for all non-zero vectors
![]() $\lambda \in \mathbb{F}_2^r$
. Let
$\lambda \in \mathbb{F}_2^r$
. Let
![]() $C$
be a coset of a subspace of
$C$
be a coset of a subspace of
![]() $\mathbb{F}_2^n$
of codimension
$\mathbb{F}_2^n$
of codimension
![]() $d$
. Let
$d$
. Let
![]() $\varepsilon \gt 0$
. If
$\varepsilon \gt 0$
. If
![]() $m \gt 4r + 8d + 4 \log _2\varepsilon ^{-1}$
then
$m \gt 4r + 8d + 4 \log _2\varepsilon ^{-1}$
then
![]() $\alpha |_{C \times C}$
takes every value in
$\alpha |_{C \times C}$
takes every value in
![]() $\mathbb{F}_2^r$
at least
$\mathbb{F}_2^r$
at least
![]() $(1 - \varepsilon )2^{-r}|C|^2$
times. In particular, if
$(1 - \varepsilon )2^{-r}|C|^2$
times. In particular, if
![]() $m \gt 4r + 8d + 4$
then
$m \gt 4r + 8d + 4$
then
![]() $\alpha |_{C \times C}$
is surjective.
$\alpha |_{C \times C}$
is surjective.
The reason for calling this lemma an algebraic counting lemma is that it is closely related to the more traditional counting results. For example, we can easily deduce that for any
![]() $\nu _1, \nu _2, \nu _3 \in \mathbb{F}_2^r$
the number of triples
$\nu _1, \nu _2, \nu _3 \in \mathbb{F}_2^r$
the number of triples
![]() $x,y,z \in \mathbb{F}_2^n$
such that
$x,y,z \in \mathbb{F}_2^n$
such that
![]() $\alpha (x,y) = \nu _1$
,
$\alpha (x,y) = \nu _1$
,
![]() $\alpha (y,z) = \nu _2$
and
$\alpha (y,z) = \nu _2$
and
![]() $\alpha (z, x) = \nu _3$
is approximately
$\alpha (z, x) = \nu _3$
is approximately
![]() $2^{-3r} \cdot 2^{3n}$
as long as
$2^{-3r} \cdot 2^{3n}$
as long as
![]() $\alpha$
is sufficiently quasirandom. In the graph-theoretic language, this corresponds to counting triangles. Similarly, Lemma 10 is related to Szemerédi’s regularity lemma.
$\alpha$
is sufficiently quasirandom. In the graph-theoretic language, this corresponds to counting triangles. Similarly, Lemma 10 is related to Szemerédi’s regularity lemma.
Proof. Suppose that the restriction
![]() $\alpha |_{C \times C}$
takes the value
$\alpha |_{C \times C}$
takes the value
![]() $u \in \mathbb{F}_2^r$
at most
$u \in \mathbb{F}_2^r$
at most
![]() $(1 - \varepsilon )2^{-r}|C|^2$
times. Then we have
$(1 - \varepsilon )2^{-r}|C|^2$
times. Then we have
 \begin{align*} (1 - \varepsilon )2^{-r-2d} & \geq \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y){\mathbb{1}}(\alpha (x,y) = u) = \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{\lambda \in \mathbb{F}_2^r} (\!-\!1)^{\lambda \cdot (\alpha (x,y) - u)}\\[5pt] &= 2^{-r} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) + 2^{-r} \sum _{\lambda \in \mathbb{F}_2^r \setminus \{0\}} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot (\alpha (x,y) - u)}\\[5pt] &= 2^{-r - 2d} + 2^{-r} \sum _{\lambda \in \mathbb{F}_2^r \setminus \{0\}} (\!-\!1)^{- \lambda \cdot u} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot \alpha (x,y)}. \end{align*}
\begin{align*} (1 - \varepsilon )2^{-r-2d} & \geq \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y){\mathbb{1}}(\alpha (x,y) = u) = \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{\lambda \in \mathbb{F}_2^r} (\!-\!1)^{\lambda \cdot (\alpha (x,y) - u)}\\[5pt] &= 2^{-r} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) + 2^{-r} \sum _{\lambda \in \mathbb{F}_2^r \setminus \{0\}} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot (\alpha (x,y) - u)}\\[5pt] &= 2^{-r - 2d} + 2^{-r} \sum _{\lambda \in \mathbb{F}_2^r \setminus \{0\}} (\!-\!1)^{- \lambda \cdot u} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot \alpha (x,y)}. \end{align*}
Using the triangle inequality, we see that
 \begin{align*} 2^{-r} \sum _{\lambda \in \mathbb{F}_2^r \setminus \{0\}} \bigg | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot \alpha (x,y)}\bigg | \geq \varepsilon 2^{-r-2d}, \end{align*}
\begin{align*} 2^{-r} \sum _{\lambda \in \mathbb{F}_2^r \setminus \{0\}} \bigg | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n}{\mathbb{1}}_C(x){\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot \alpha (x,y)}\bigg | \geq \varepsilon 2^{-r-2d}, \end{align*}
so by averaging we obtain a non-zero
![]() $\lambda$
such that
$\lambda$
such that
Applying Cauchy-Schwarz inequalityFootnote 3 we obtain
 \begin{align*} \varepsilon ^2 2^{-2r-4d} &\leq \bigg | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n}{\mathbb{1}}_C(x) \Big ( \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y \in \mathbb{F}_2^n}{\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot \alpha (x,y)}\Big )\bigg |^2 \leq \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n}\Big | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y \in \mathbb{F}_2^n}{\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot \alpha (x,y)}\Big |^2\\[5pt] &= \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y, y' \in \mathbb{F}_2^n}{\mathbb{1}}_C(y){\mathbb{1}}_C(y') (\!-\!1)^{\lambda \cdot \alpha (x,y + y')}. \end{align*}
\begin{align*} \varepsilon ^2 2^{-2r-4d} &\leq \bigg | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n}{\mathbb{1}}_C(x) \Big ( \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y \in \mathbb{F}_2^n}{\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot \alpha (x,y)}\Big )\bigg |^2 \leq \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n}\Big | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y \in \mathbb{F}_2^n}{\mathbb{1}}_C(y) (\!-\!1)^{\lambda \cdot \alpha (x,y)}\Big |^2\\[5pt] &= \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y, y' \in \mathbb{F}_2^n}{\mathbb{1}}_C(y){\mathbb{1}}_C(y') (\!-\!1)^{\lambda \cdot \alpha (x,y + y')}. \end{align*}
Another application of Cauchy-Schwarz inequality gives
 \begin{align*} \varepsilon ^4 2^{-4r-8d} & \leq \Big | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y, y' \in \mathbb{F}_2^n}{\mathbb{1}}_C(y){\mathbb{1}}_C(y') \Big ( \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n} (\!-\!1)^{\lambda \cdot \alpha (x,y + y')}\Big )\Big |^2 \leq \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y, y' \in \mathbb{F}_2^n} \Big | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n} (\!-\!1)^{\lambda \cdot \alpha (x,y + y')}\Big |^2\\[5pt] &= \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,x' \in \mathbb{F}_2^n} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y, y' \in \mathbb{F}_2^n} (\!-\!1)^{\lambda \cdot \alpha (x + x',y + y')} = \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n} (\!-\!1)^{\lambda \cdot \alpha (x,y)} \end{align*}
\begin{align*} \varepsilon ^4 2^{-4r-8d} & \leq \Big | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y, y' \in \mathbb{F}_2^n}{\mathbb{1}}_C(y){\mathbb{1}}_C(y') \Big ( \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n} (\!-\!1)^{\lambda \cdot \alpha (x,y + y')}\Big )\Big |^2 \leq \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y, y' \in \mathbb{F}_2^n} \Big | \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x \in \mathbb{F}_2^n} (\!-\!1)^{\lambda \cdot \alpha (x,y + y')}\Big |^2\\[5pt] &= \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,x' \in \mathbb{F}_2^n} \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{y, y' \in \mathbb{F}_2^n} (\!-\!1)^{\lambda \cdot \alpha (x + x',y + y')} = \def \mbl{\mathop{\mathbb{E}}\limits }\mbl _{x,y \in \mathbb{F}_2^n} (\!-\!1)^{\lambda \cdot \alpha (x,y)} \end{align*}
which equals
![]() $2^{-\textrm{rank}(\lambda \cdot \alpha )}$
by Lemma 7
(i). Hence
$2^{-\textrm{rank}(\lambda \cdot \alpha )}$
by Lemma 7
(i). Hence
![]() $\varepsilon ^4 2^{-4r-8d} \leq 2^{-m}$
so
$\varepsilon ^4 2^{-4r-8d} \leq 2^{-m}$
so
![]() $m \leq 4r + 8d + 4 \log _2\varepsilon ^{-1}$
, which is a contradiction.
$m \leq 4r + 8d + 4 \log _2\varepsilon ^{-1}$
, which is a contradiction.
3. Example
Recall that
![]() $n$
is a fixed positive integer, which we think of as large, and that
$n$
is a fixed positive integer, which we think of as large, and that
![]() $G = \mathbb{F}_2^n$
. Let
$G = \mathbb{F}_2^n$
. Let
![]() $e_1, \ldots, e_n$
be the standard basis of
$e_1, \ldots, e_n$
be the standard basis of
![]() $G$
. Our example will be the multilinear form
$G$
. Our example will be the multilinear form
![]() $\phi \colon G^4 \to \mathbb{F}_2$
defined as
$\phi \colon G^4 \to \mathbb{F}_2$
defined as
where the coordinates of vectors are taken with the respect to the fixed basis
![]() $e_1, \ldots, e_n$
. We first show that
$e_1, \ldots, e_n$
. We first show that
![]() $\phi$
is approximately symmetric.
$\phi$
is approximately symmetric.
Lemma 12.
The multilinear form
![]() $\phi$
satisfies
$\phi$
satisfies
![]() $\phi = \phi \circ (1\,\,2)$
,
$\phi = \phi \circ (1\,\,2)$
,
![]() $\phi = \phi \circ (1\,\,3)$
and
$\phi = \phi \circ (1\,\,3)$
and
where
Proof. For each
![]() $i$
and
$i$
and
![]() $j$
the expression
$j$
the expression
![]() $x_i y_j z_j w_i + x_j y_i z_j w_i + x_j y_j z_i w_i$
is symmetric in
$x_i y_j z_j w_i + x_j y_i z_j w_i + x_j y_j z_i w_i$
is symmetric in
![]() $x,y$
and
$x,y$
and
![]() $z$
and hence the equalities
$z$
and hence the equalities
![]() $\phi = \phi \circ (1\,\,2)$
and
$\phi = \phi \circ (1\,\,2)$
and
![]() $\phi = \phi \circ (1\,\,3)$
follow immediately. For the remaining transposition
$\phi = \phi \circ (1\,\,3)$
follow immediately. For the remaining transposition
![]() $(1\,\,4)$
we perform some algebraic manipulation
$(1\,\,4)$
we perform some algebraic manipulation
 \begin{align*} \phi (x, y, z, w) &+ \phi (w, y, z, x) \\ & = \sum _{1 \leq i \lt j \leq n} \Big ((x_i y_j z_j w_i + x_j y_i z_j w_i + x_j y_j z_i w_i) + (w_i y_j z_j x_i + w_j y_i z_j x_i + w_j y_j z_i x_i)\Big ) \\[5pt] &= \sum _{1 \leq i \lt j \leq n} \Big (x_j y_i z_j w_i + x_j y_j z_i w_i + x_i y_i z_j w_j + x_i y_j z_i w_j\Big )\\[5pt] &= \sum _{1 \leq i \lt j \leq n} \Big (x_j y_i z_j w_i + x_i y_j z_i w_j\Big ) + \sum _{1 \leq i \lt j \leq n} \Big (x_j y_j z_i w_i + x_i y_i z_j w_j\Big )\\[5pt] &= \Big (\sum _{i,j \in [n] \colon i \not = j} x_j y_i z_j w_i \Big ) + \Big (\sum _{i,j \in [n] \colon i \not = j} x_j y_j z_i w_i \Big )\\[5pt] &= \Big (\sum _{i,j \in [n] \colon i \not = j} x_j y_i z_j w_i \Big ) + \Big (\sum _{i,j \in [n] \colon i \not = j} x_j y_j z_i w_i \Big ) + 2 \cdot \Big (\sum _{i \in [n]} x_i y_i z_i w_i\Big )\\[5pt] &= \Big (\sum _{i,j \in [n]} x_j y_i z_j w_i \Big ) + \Big (\sum _{i,j \in [n]} x_j y_j z_i w_i \Big )\\[5pt] &= \Big (\sum _{j \in [n]} x_j z_j \Big ) \Big (\sum _{i \in [n]} y_i w_i \Big ) + \Big (\sum _{j \in [n]} x_j y_j \Big ) \Big (\sum _{i \in [n]} z_i w_i \Big )\\[5pt] &= \rho (x,z) \rho (y,w) + \rho (x,y) \rho (z,w), \end{align*}
\begin{align*} \phi (x, y, z, w) &+ \phi (w, y, z, x) \\ & = \sum _{1 \leq i \lt j \leq n} \Big ((x_i y_j z_j w_i + x_j y_i z_j w_i + x_j y_j z_i w_i) + (w_i y_j z_j x_i + w_j y_i z_j x_i + w_j y_j z_i x_i)\Big ) \\[5pt] &= \sum _{1 \leq i \lt j \leq n} \Big (x_j y_i z_j w_i + x_j y_j z_i w_i + x_i y_i z_j w_j + x_i y_j z_i w_j\Big )\\[5pt] &= \sum _{1 \leq i \lt j \leq n} \Big (x_j y_i z_j w_i + x_i y_j z_i w_j\Big ) + \sum _{1 \leq i \lt j \leq n} \Big (x_j y_j z_i w_i + x_i y_i z_j w_j\Big )\\[5pt] &= \Big (\sum _{i,j \in [n] \colon i \not = j} x_j y_i z_j w_i \Big ) + \Big (\sum _{i,j \in [n] \colon i \not = j} x_j y_j z_i w_i \Big )\\[5pt] &= \Big (\sum _{i,j \in [n] \colon i \not = j} x_j y_i z_j w_i \Big ) + \Big (\sum _{i,j \in [n] \colon i \not = j} x_j y_j z_i w_i \Big ) + 2 \cdot \Big (\sum _{i \in [n]} x_i y_i z_i w_i\Big )\\[5pt] &= \Big (\sum _{i,j \in [n]} x_j y_i z_j w_i \Big ) + \Big (\sum _{i,j \in [n]} x_j y_j z_i w_i \Big )\\[5pt] &= \Big (\sum _{j \in [n]} x_j z_j \Big ) \Big (\sum _{i \in [n]} y_i w_i \Big ) + \Big (\sum _{j \in [n]} x_j y_j \Big ) \Big (\sum _{i \in [n]} z_i w_i \Big )\\[5pt] &= \rho (x,z) \rho (y,w) + \rho (x,y) \rho (z,w), \end{align*}
as desired.
Since the transpositions
![]() $(1\,\,2), (1\,\,3)$
and
$(1\,\,2), (1\,\,3)$
and
![]() $(1\,\,4)$
generate the whole symmetric group
$(1\,\,4)$
generate the whole symmetric group
![]() $\textrm{Sym}_4$
we immediately deduce that
$\textrm{Sym}_4$
we immediately deduce that
![]() $\phi$
is 3-approximately symmetric.
$\phi$
is 3-approximately symmetric.
Corollary 13.
For any permutation
![]() $\pi \in \textrm{Sym}_4$
we have
$\pi \in \textrm{Sym}_4$
we have
![]() ${prank} \Big (\phi + \phi \circ \pi \Big ) \leq 3$
.
${prank} \Big (\phi + \phi \circ \pi \Big ) \leq 3$
.
Proof. Let
![]() $V$
be the vector space consisting of the multilinear forms on
$V$
be the vector space consisting of the multilinear forms on
![]() $G^4$
of the shape
$G^4$
of the shape
![]() $\lambda _1 \rho (x,y) \rho (z,w) + \lambda _2\rho (x,z) \rho (y,w) + \lambda _3 \rho (x,w) \rho (y,z)$
for some scalars
$\lambda _1 \rho (x,y) \rho (z,w) + \lambda _2\rho (x,z) \rho (y,w) + \lambda _3 \rho (x,w) \rho (y,z)$
for some scalars
![]() $\lambda _1, \lambda _2, \lambda _3 \in \mathbb{F}_2$
. Since
$\lambda _1, \lambda _2, \lambda _3 \in \mathbb{F}_2$
. Since
![]() $\rho$
is a symmetric bilinear form it follows that
$\rho$
is a symmetric bilinear form it follows that
![]() $V$
is invariant under the action of
$V$
is invariant under the action of
![]() $\textrm{Sym}_4$
. The lemma above shows in particular that
$\textrm{Sym}_4$
. The lemma above shows in particular that
![]() $\phi + \phi \circ \pi \in V$
whenever
$\phi + \phi \circ \pi \in V$
whenever
![]() $\pi$
is one of the transpositions
$\pi$
is one of the transpositions
![]() $(1\,\,2), (1\,\,3)$
and
$(1\,\,2), (1\,\,3)$
and
![]() $(1\,\,4)$
. Let
$(1\,\,4)$
. Let
![]() $\pi \in \textrm{Sym}_4$
now be an arbitrary permutation. The transpositions
$\pi \in \textrm{Sym}_4$
now be an arbitrary permutation. The transpositions
![]() $(1\,\,2), (1\,\,3)$
and
$(1\,\,2), (1\,\,3)$
and
![]() $(1\,\,4)$
generate
$(1\,\,4)$
generate
![]() $\textrm{Sym}_4$
so we can write
$\textrm{Sym}_4$
so we can write
![]() $\pi = \tau _1 \circ \tau _2 \circ \ldots \circ \tau _r$
for some
$\pi = \tau _1 \circ \tau _2 \circ \ldots \circ \tau _r$
for some
![]() $\tau _1, \ldots, \tau _r \in \{(1\,\,2), (1\,\,3), (1\,\,4)\}$
. Then we have
$\tau _1, \ldots, \tau _r \in \{(1\,\,2), (1\,\,3), (1\,\,4)\}$
. Then we have
 \begin{align*} \phi \circ \pi + \phi = &\sum _{i \in [r]}\Big (\phi \circ \tau _i \circ \tau _{i+1} \circ \ldots \circ \tau _r + \phi \circ \tau _{i+1} \circ \tau _{i+2} \circ \ldots \circ \tau _r\Big )\\[5pt] = &\sum _{i \in [r]} \Big (\phi \circ \tau _i + \phi \Big ) \circ \tau _{i+1} \circ \ldots \circ \tau _r \end{align*}
\begin{align*} \phi \circ \pi + \phi = &\sum _{i \in [r]}\Big (\phi \circ \tau _i \circ \tau _{i+1} \circ \ldots \circ \tau _r + \phi \circ \tau _{i+1} \circ \tau _{i+2} \circ \ldots \circ \tau _r\Big )\\[5pt] = &\sum _{i \in [r]} \Big (\phi \circ \tau _i + \phi \Big ) \circ \tau _{i+1} \circ \ldots \circ \tau _r \end{align*}
which is a sum of
![]() $r$
forms, each of which is a member of
$r$
forms, each of which is a member of
![]() $V$
. Hence
$V$
. Hence
![]() $\phi + \phi \circ \pi \in V$
for all
$\phi + \phi \circ \pi \in V$
for all
![]() $\pi \in \textrm{Sym}_4$
. Since the partition rank of forms in
$\pi \in \textrm{Sym}_4$
. Since the partition rank of forms in
![]() $V$
is at most 3, the proof is complete.
$V$
is at most 3, the proof is complete.
In the rest of this section, we show that the map
![]() $\phi$
is necessarily far from any symmetric multilinear form.
$\phi$
is necessarily far from any symmetric multilinear form.
Theorem 14.
Let
![]() $r \geq 1$
be a positive integer. Assume that
$r \geq 1$
be a positive integer. Assume that
![]() $n \geq (1000r)^3$
. For any symmetric multilinear form
$n \geq (1000r)^3$
. For any symmetric multilinear form
![]() $\sigma \colon G^4 \to \mathbb{F}_2$
we have
$\sigma \colon G^4 \to \mathbb{F}_2$
we have
![]() ${prank}(\phi + \sigma ) \gt r$
.
${prank}(\phi + \sigma ) \gt r$
.
Proof. Let
![]() $\sigma \colon G^4 \to \mathbb{F}_2$
be a symmetric multilinear form. Suppose on the contrary that
$\sigma \colon G^4 \to \mathbb{F}_2$
be a symmetric multilinear form. Suppose on the contrary that
![]() $\textrm{prank}(\phi + \sigma ) \leq r$
. Then we may find linear forms
$\textrm{prank}(\phi + \sigma ) \leq r$
. Then we may find linear forms
![]() $u^1_1, \ldots,$
$u^1_1, \ldots,$
![]() $u^1_r,$
$u^1_r,$
![]() $\ldots,$
$\ldots,$
![]() $u^4_1, \ldots, u^4_r$
, bilinear forms
$u^4_1, \ldots, u^4_r$
, bilinear forms
![]() $\gamma ^1_1, \ldots,$
$\gamma ^1_1, \ldots,$
![]() $\gamma ^1_r, \ldots,$
$\gamma ^1_r, \ldots,$
![]() $\gamma ^3_1, \ldots, \gamma ^3_r$
and
$\gamma ^3_1, \ldots, \gamma ^3_r$
and
![]() $\tilde{\gamma }^1_1, \ldots,$
$\tilde{\gamma }^1_1, \ldots,$
![]() $\tilde{\gamma }^1_r, \ldots,$
$\tilde{\gamma }^1_r, \ldots,$
![]() $\tilde{\gamma }^3_1, \ldots, \tilde{\gamma }^3_r$
, and trilinear forms
$\tilde{\gamma }^3_1, \ldots, \tilde{\gamma }^3_r$
, and trilinear forms
![]() $\theta ^1_1, \ldots,$
$\theta ^1_1, \ldots,$
![]() $\theta ^1_r, \ldots,$
$\theta ^1_r, \ldots,$
![]() $\theta ^4_1, \ldots, \theta ^4_r$
(we set some of the forms to be 0 to have a single parameter
$\theta ^4_1, \ldots, \theta ^4_r$
(we set some of the forms to be 0 to have a single parameter
![]() $r$
instead of a separate count for each sequence of forms) on the space
$r$
instead of a separate count for each sequence of forms) on the space
![]() $G$
such that
$G$
such that
 \begin{align*} \phi (x,y,z,w) & = \sigma (x,y,z,w) + \sum _{i \in [r]} u^1_i(x) \theta ^1_i(y,z,w) + \sum _{i \in [r]} u^2_i(y) \theta ^2_i(x,z,w)\\[5pt] & \quad + \sum _{i \in [r]} u^3_i(z) \theta ^3_i(x,y,w) + \sum _{i \in [r]} u^4_i(w) \theta ^4_i(x, y,z)\\[5pt] & \quad + \sum _{i \in [r]}\gamma ^1_i(x,y) \tilde{\gamma }^1_i(z,w) + \sum _{i \in [r]}\gamma ^2_i(x,z) \tilde{\gamma }^2_i(y,w) + \sum _{i \in [r]}\gamma ^3_i(x,w) \tilde{\gamma }^3_i(y,z) \end{align*}
\begin{align*} \phi (x,y,z,w) & = \sigma (x,y,z,w) + \sum _{i \in [r]} u^1_i(x) \theta ^1_i(y,z,w) + \sum _{i \in [r]} u^2_i(y) \theta ^2_i(x,z,w)\\[5pt] & \quad + \sum _{i \in [r]} u^3_i(z) \theta ^3_i(x,y,w) + \sum _{i \in [r]} u^4_i(w) \theta ^4_i(x, y,z)\\[5pt] & \quad + \sum _{i \in [r]}\gamma ^1_i(x,y) \tilde{\gamma }^1_i(z,w) + \sum _{i \in [r]}\gamma ^2_i(x,z) \tilde{\gamma }^2_i(y,w) + \sum _{i \in [r]}\gamma ^3_i(x,w) \tilde{\gamma }^3_i(y,z) \end{align*}
holds for all
![]() $x,y,z,w \in G$
. Let us pass to the subspace
$x,y,z,w \in G$
. Let us pass to the subspace
![]() $U = \{x \in G \colon (\forall d \in [4])(\forall i \in [r]) u^d_i(x) = 0\}$
which has codimension at most
$U = \{x \in G \colon (\forall d \in [4])(\forall i \in [r]) u^d_i(x) = 0\}$
which has codimension at most
![]() $4r$
. When
$4r$
. When
![]() $x,y,z,w \in U$
then
$x,y,z,w \in U$
then
In the rest of proof we deal with bilinear forms primarily so we simply use the word rank instead of partition rank as the usual notion of rank is equivalent to the partition rank, as remarked earlier. We now gather all
![]() $6r$
bilinear forms
$6r$
bilinear forms
![]() $\gamma ^1_1, \ldots, \tilde{\gamma }^3_r$
above into a single sequence and apply the bilinear regularity lemma. Let
$\gamma ^1_1, \ldots, \tilde{\gamma }^3_r$
above into a single sequence and apply the bilinear regularity lemma. Let
![]() $m \geq 1$
be an integer to be chosen later. Provided that
$m \geq 1$
be an integer to be chosen later. Provided that
is satisfied, we may assume that
![]() $\textrm{rank} \rho |_{U \times U} \geq 24rm + m$
(recall that
$\textrm{rank} \rho |_{U \times U} \geq 24rm + m$
(recall that
![]() $\textrm{rank} \rho = n$
). Lemma 10 allows us to find a subspace
$\textrm{rank} \rho = n$
). Lemma 10 allows us to find a subspace
![]() $U' \leq U$
of codimension at most
$U' \leq U$
of codimension at most
![]() $12rm$
inside
$12rm$
inside
![]() $U$
, a positive integer
$U$
, a positive integer
![]() $s \leq 6r$
, bilinear forms
$s \leq 6r$
, bilinear forms
![]() $\alpha _1, \ldots, \alpha _s \colon U' \times U' \to \mathbb{F}_2$
such that every map among
$\alpha _1, \ldots, \alpha _s \colon U' \times U' \to \mathbb{F}_2$
such that every map among
![]() $\gamma ^1_1, \ldots, \tilde{\gamma }^3_r$
equals a linear combination of
$\gamma ^1_1, \ldots, \tilde{\gamma }^3_r$
equals a linear combination of
![]() $\alpha _1, \ldots, \alpha _s$
and
$\alpha _1, \ldots, \alpha _s$
and
![]() $\rho |_{U' \times U'}$
on
$\rho |_{U' \times U'}$
on
![]() $U' \times U'$
and all non-zero linear combinations of
$U' \times U'$
and all non-zero linear combinations of
![]() $\alpha _1, \ldots, \alpha _s$
and
$\alpha _1, \ldots, \alpha _s$
and
![]() $\rho |_{U' \times U'}$
have rank at least
$\rho |_{U' \times U'}$
have rank at least
![]() $m$
.
$m$
.
Expressing maps
![]() $\gamma ^1_1, \ldots, \tilde{\gamma }^3_r$
in terms of these bilinear forms, we conclude that whenever
$\gamma ^1_1, \ldots, \tilde{\gamma }^3_r$
in terms of these bilinear forms, we conclude that whenever
![]() $x,y,z,w \in U'$
$x,y,z,w \in U'$
 \begin{align} \phi (x,y,z,w) & = \sigma (x,y,z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda '_{ij} \alpha _i(x,z) \alpha _j(y,w) \nonumber \\[5pt] & \quad + \sum _{i,j \in [s]} \lambda ''_{ij} \alpha _i(x,w) \alpha _j(y,z) + \rho (x,y) \beta _1(z,w) + \rho (x,z) \beta _2(y,w) + \rho (x,w) \beta _3(y,z) \nonumber \\[5pt] & \quad + \rho (y,z) \beta _4(x,w) + \rho (y,w) \beta _5(x,z) + \rho (z,w) \beta _6(x,y) \end{align}
\begin{align} \phi (x,y,z,w) & = \sigma (x,y,z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda '_{ij} \alpha _i(x,z) \alpha _j(y,w) \nonumber \\[5pt] & \quad + \sum _{i,j \in [s]} \lambda ''_{ij} \alpha _i(x,w) \alpha _j(y,z) + \rho (x,y) \beta _1(z,w) + \rho (x,z) \beta _2(y,w) + \rho (x,w) \beta _3(y,z) \nonumber \\[5pt] & \quad + \rho (y,z) \beta _4(x,w) + \rho (y,w) \beta _5(x,z) + \rho (z,w) \beta _6(x,y) \end{align}
where
![]() $\lambda _{ij}, \lambda '_{ij}, \lambda ''_{ij} \in \mathbb{F}_2$
are suitable coefficients and
$\lambda _{ij}, \lambda '_{ij}, \lambda ''_{ij} \in \mathbb{F}_2$
are suitable coefficients and
![]() $\beta _1, \ldots, \beta _6 \colon U' \times U' \to \mathbb{F}_2$
are suitable bilinear forms.
$\beta _1, \ldots, \beta _6 \colon U' \times U' \to \mathbb{F}_2$
are suitable bilinear forms.
We now use the approximate symmetry properties of
![]() $\phi$
in order to deduce that the coefficients
$\phi$
in order to deduce that the coefficients
![]() $\lambda _{ij}, \lambda '_{ij}, \lambda ''_{ij}$
are symmetric in
$\lambda _{ij}, \lambda '_{ij}, \lambda ''_{ij}$
are symmetric in
![]() $i$
and
$i$
and
![]() $j$
and that forms
$j$
and that forms
![]() $\alpha _i$
are essentially symmetric. This will eventually allow us to simplify the expression in (4). The identity
$\alpha _i$
are essentially symmetric. This will eventually allow us to simplify the expression in (4). The identity
![]() $\phi + \phi \circ (1\,\,2) = 0$
will be used to prove the following claim.
$\phi + \phi \circ (1\,\,2) = 0$
will be used to prove the following claim.
Claim 15.
Assume
![]() $m \geq 40(s + 1)$
.
$m \geq 40(s + 1)$
.
-
i. There exists a subspace
 $V^1 \leq U'$
such that
$V^1 \leq U'$
such that
 $\dim V^1 \geq \dim U' - 2s^2 - 4s$
and for each
$\dim V^1 \geq \dim U' - 2s^2 - 4s$
and for each
 $j \in [s]$
the bilinear form
$j \in [s]$
the bilinear form
 $\sum _{i \in [s]}\lambda _{ij} \alpha _i$
is symmetric on
$\sum _{i \in [s]}\lambda _{ij} \alpha _i$
is symmetric on
 $V^1 \times V^1$
.
$V^1 \times V^1$
. -
ii. For all
 $i,j \in [s]$
,
$i,j \in [s]$
,
 $\lambda '_{ij} = \lambda ''_{ji}$
.
$\lambda '_{ij} = \lambda ''_{ji}$
.
Proof. Using the fact that
![]() $\phi + \phi \circ (1\,\,2) = 0$
and (4) we get
$\phi + \phi \circ (1\,\,2) = 0$
and (4) we get
 \begin{align} 0 = & \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} (\alpha _i(x,y) + \alpha _i(y,x))\Big ) \alpha _j(z,w) + \sum _{i,j \in [s]} (\lambda '_{ij}+ \lambda ''_{ji}) \alpha _i(x,z) \alpha _j(y,w) \nonumber \\[5pt] &+ \sum _{i \in [s]} \alpha _i(x,w)\Big (\sum _{j \in [s]}(\lambda ''_{ij} + \lambda '_{ji}) \alpha _j(y,z)\Big )\nonumber \\[5pt] &+\rho (x,z) (\beta _2(y,w) + \beta _4(y,w)) + \rho (x,w) (\beta _3(y,z) + \beta _5(y,z)) + \rho (y,z) (\beta _4(x,w) + \beta _2(x,w))\nonumber \\[5pt] & + \rho (y,w) (\beta _5(x,z) + \beta _3(x,z)) + \rho (z,w) (\beta _6(x,y) + \beta _6(y,x)) \end{align}
\begin{align} 0 = & \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} (\alpha _i(x,y) + \alpha _i(y,x))\Big ) \alpha _j(z,w) + \sum _{i,j \in [s]} (\lambda '_{ij}+ \lambda ''_{ji}) \alpha _i(x,z) \alpha _j(y,w) \nonumber \\[5pt] &+ \sum _{i \in [s]} \alpha _i(x,w)\Big (\sum _{j \in [s]}(\lambda ''_{ij} + \lambda '_{ji}) \alpha _j(y,z)\Big )\nonumber \\[5pt] &+\rho (x,z) (\beta _2(y,w) + \beta _4(y,w)) + \rho (x,w) (\beta _3(y,z) + \beta _5(y,z)) + \rho (y,z) (\beta _4(x,w) + \beta _2(x,w))\nonumber \\[5pt] & + \rho (y,w) (\beta _5(x,z) + \beta _3(x,z)) + \rho (z,w) (\beta _6(x,y) + \beta _6(y,x)) \end{align}
for all
![]() $x,y,z,w \in U'$
.
$x,y,z,w \in U'$
.
Proof of (i). Let
![]() $j \in [s]$
be given. Since any non-zero linear combination of
$j \in [s]$
be given. Since any non-zero linear combination of
![]() $\rho |_{U' \times U'}, \alpha _1, \ldots, \alpha _s$
has rank at least
$\rho |_{U' \times U'}, \alpha _1, \ldots, \alpha _s$
has rank at least
![]() $m \gt 4(s + 2)$
by Lemma 11 we can find
$m \gt 4(s + 2)$
by Lemma 11 we can find
![]() $z,w \in U'$
such that
$z,w \in U'$
such that
![]() $\rho (z,w) = 0$
,
$\rho (z,w) = 0$
,
![]() $\alpha _i(z,w) = 0$
for all
$\alpha _i(z,w) = 0$
for all
![]() $i \not = j$
and
$i \not = j$
and
![]() $\alpha _j(z,w) = 1$
. Using this choice of
$\alpha _j(z,w) = 1$
. Using this choice of
![]() $z,w$
in (5) we obtain
$z,w$
in (5) we obtain
 \begin{align*} \sum _{i \in [s]}\lambda _{ij} (\alpha _i(x,y) + \alpha _i(y,x)) &= \sum _{i \in [s]}\alpha _i(x,z) \Big (\sum _{\ell \in [s]} (\lambda '_{i \ell }+ \lambda ''_{\ell i}) \alpha _\ell (y,w)\Big ) \\[5pt] & \quad + \sum _{i \in [s]} \alpha _i(x,w) \Big (\sum _{\ell \in [s]} (\lambda ''_{i\ell } + \lambda '_{\ell i})\alpha _\ell (y,z)\Big ) +\rho (x,z) (\beta _2(y,w)\\[5pt] & \quad + \beta _4(y,w)) + \rho (x,w) (\beta _3(y,z) + \beta _5(y,z)) + \rho (y,z) (\beta _4(x,w) \\[5pt] & \quad+ \beta _2(x,w)) + \rho (y,w) (\beta _5(x,z) + \beta _3(x,z)) \end{align*}
\begin{align*} \sum _{i \in [s]}\lambda _{ij} (\alpha _i(x,y) + \alpha _i(y,x)) &= \sum _{i \in [s]}\alpha _i(x,z) \Big (\sum _{\ell \in [s]} (\lambda '_{i \ell }+ \lambda ''_{\ell i}) \alpha _\ell (y,w)\Big ) \\[5pt] & \quad + \sum _{i \in [s]} \alpha _i(x,w) \Big (\sum _{\ell \in [s]} (\lambda ''_{i\ell } + \lambda '_{\ell i})\alpha _\ell (y,z)\Big ) +\rho (x,z) (\beta _2(y,w)\\[5pt] & \quad + \beta _4(y,w)) + \rho (x,w) (\beta _3(y,z) + \beta _5(y,z)) + \rho (y,z) (\beta _4(x,w) \\[5pt] & \quad+ \beta _2(x,w)) + \rho (y,w) (\beta _5(x,z) + \beta _3(x,z)) \end{align*}
for all
![]() $x,y \in U'$
. By Lemma 7
(iii) we conclude that
$x,y \in U'$
. By Lemma 7
(iii) we conclude that
![]() $\sum _{i \in [s]}\lambda _{ij} (\alpha _i(x,y) + \alpha _i(y,x))$
has rank at most
$\sum _{i \in [s]}\lambda _{ij} (\alpha _i(x,y) + \alpha _i(y,x))$
has rank at most
![]() $2s + 4$
, so by Lemma 8 we may find a subspace
$2s + 4$
, so by Lemma 8 we may find a subspace
![]() $U'_j \leq U'$
with
$U'_j \leq U'$
with
![]() $\dim U'_j \geq \dim U' - 2s-4$
such that
$\dim U'_j \geq \dim U' - 2s-4$
such that
![]() $\sum _{i \in [s]}\lambda _{ij} (\alpha _i(x,y) + \alpha _i(y,x)) = 0$
when
$\sum _{i \in [s]}\lambda _{ij} (\alpha _i(x,y) + \alpha _i(y,x)) = 0$
when
![]() $x,y \in U'_j$
. We may take
$x,y \in U'_j$
. We may take
![]() $V^1 = \cap _{j \in [s]} U'_j$
.
$V^1 = \cap _{j \in [s]} U'_j$
.
Proof of (ii). Let
![]() $i, j \in [s]$
be given. This time we find elements
$i, j \in [s]$
be given. This time we find elements
![]() $x,y,z,w \in U'$
such that
$x,y,z,w \in U'$
such that
![]() $\alpha _1, \ldots, \alpha _s$
and
$\alpha _1, \ldots, \alpha _s$
and
![]() $\rho$
are equal to 0 at all 6 points in the set
$\rho$
are equal to 0 at all 6 points in the set
![]() $\{(x,y), (x,z), (x,w), (y,z), (y,w), (z,w)\}$
, with the two exceptions being
$\{(x,y), (x,z), (x,w), (y,z), (y,w), (z,w)\}$
, with the two exceptions being
![]() $\alpha _i(x,z) = \alpha _j(y,w) = 1$
. Once we have such elements
$\alpha _i(x,z) = \alpha _j(y,w) = 1$
. Once we have such elements
![]() $x,y,z,w$
we use them in (5) which reduces to just
$x,y,z,w$
we use them in (5) which reduces to just
![]() $\lambda '_{ij}+ \lambda ''_{ji} = 0$
, proving that
$\lambda '_{ij}+ \lambda ''_{ji} = 0$
, proving that
![]() $\lambda '_{ij} = \lambda ''_{ji}$
, which is what we are after. To obtain such a quadruple of elements
$\lambda '_{ij} = \lambda ''_{ji}$
, which is what we are after. To obtain such a quadruple of elements
![]() $x,y,z,w$
, provided
$x,y,z,w$
, provided
![]() $m \gt 4(s + 2)$
, we first apply Lemma 11 to obtain
$m \gt 4(s + 2)$
, we first apply Lemma 11 to obtain
![]() $(x,z) \in U' \times U'$
such that
$(x,z) \in U' \times U'$
such that
![]() $\rho (x,z) = 0$
,
$\rho (x,z) = 0$
,
![]() $\alpha _\ell (x,z) = 0$
when
$\alpha _\ell (x,z) = 0$
when
![]() $\ell \not = i$
and
$\ell \not = i$
and
![]() $\alpha _i(x,z) = 1$
. Then we define a subspace
$\alpha _i(x,z) = 1$
. Then we define a subspace
Provided
![]() $m \gt 4(s + 2) + 8(4s + 2)$
, we may use Lemma 11 one more time to find
$m \gt 4(s + 2) + 8(4s + 2)$
, we may use Lemma 11 one more time to find
![]() $(y,w) \in \tilde{U} \times \tilde{U}$
such that
$(y,w) \in \tilde{U} \times \tilde{U}$
such that
![]() $\rho (y,w) = 0$
,
$\rho (y,w) = 0$
,
![]() $\alpha _\ell (y,w) = 0$
when
$\alpha _\ell (y,w) = 0$
when
![]() $\ell \not = j$
and
$\ell \not = j$
and
![]() $\alpha _j(y,w) = 1$
, completing the proof.
$\alpha _j(y,w) = 1$
, completing the proof.
Next, we use the second symmetry condition
![]() $\phi + \phi \circ (1\,\,3) = 0$
in a similar manner to prove the following claim. We remark that we make use of Claim 15 in the proof.
$\phi + \phi \circ (1\,\,3) = 0$
in a similar manner to prove the following claim. We remark that we make use of Claim 15 in the proof.
Claim 16.
Assume
![]() $m \geq 100(s^2 + s + 1)$
.
$m \geq 100(s^2 + s + 1)$
.
-
i. There exists a subspace
 $V^2 \leq V^1$
such that
$V^2 \leq V^1$
such that
 $\dim V^2 \geq \dim V^1 - 2s^2 - 4s$
and
$\dim V^2 \geq \dim V^1 - 2s^2 - 4s$
and
 $\sum _{i \in [s]} \lambda '_{ij} \alpha _i$
is symmetric for all
$\sum _{i \in [s]} \lambda '_{ij} \alpha _i$
is symmetric for all
 $j \in [s]$
on
$j \in [s]$
on
 $V^2 \times V^2$
.
$V^2 \times V^2$
. -
ii. For all
 $i,j \in [s]$
,
$i,j \in [s]$
,
 $\lambda _{ij} = \lambda ''_{ji}$
.
$\lambda _{ij} = \lambda ''_{ji}$
.
Proof. The identity
![]() $\phi + \phi \circ (1\,\,3) = 0$
coupled with (4) gives
$\phi + \phi \circ (1\,\,3) = 0$
coupled with (4) gives
 \begin{align} 0 &= \sum _{i,j \in [s]} (\lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \lambda ''_{ji} \alpha _i(y,x)\alpha _j(z,w)) + \sum _{i,j \in [s]} \lambda '_{ij} (\alpha _i(x,z) + \alpha _i(z,x))\alpha _j(y,w) \nonumber \\[5pt] &\quad + \sum _{i,j \in [s]} (\lambda ''_{ij} \alpha _i(x,w) \alpha _j(y,z) + \lambda _{ji} \alpha _i(x,w) \alpha _j(z,y))\nonumber \\[5pt] &\quad +\rho (x,y) (\beta _1(z,w) + \beta _4(z,w)) + \rho (x,w) (\beta _3(y,z) + \beta _6(z,y)) + \rho (y,z) (\beta _4(x,w) + \beta _1(x,w))\nonumber \\[5pt] &\quad + \rho (y,w) (\beta _5(x,z) + \beta _5(z,x)) + \rho (z,w) (\beta _6(x,y) + \beta _3(y,x)) \end{align}
\begin{align} 0 &= \sum _{i,j \in [s]} (\lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \lambda ''_{ji} \alpha _i(y,x)\alpha _j(z,w)) + \sum _{i,j \in [s]} \lambda '_{ij} (\alpha _i(x,z) + \alpha _i(z,x))\alpha _j(y,w) \nonumber \\[5pt] &\quad + \sum _{i,j \in [s]} (\lambda ''_{ij} \alpha _i(x,w) \alpha _j(y,z) + \lambda _{ji} \alpha _i(x,w) \alpha _j(z,y))\nonumber \\[5pt] &\quad +\rho (x,y) (\beta _1(z,w) + \beta _4(z,w)) + \rho (x,w) (\beta _3(y,z) + \beta _6(z,y)) + \rho (y,z) (\beta _4(x,w) + \beta _1(x,w))\nonumber \\[5pt] &\quad + \rho (y,w) (\beta _5(x,z) + \beta _5(z,x)) + \rho (z,w) (\beta _6(x,y) + \beta _3(y,x)) \end{align}
for all
![]() $x,y,z,w \in U'$
.
$x,y,z,w \in U'$
.
Proof of (i). Let
![]() $j \in [s]$
be given. Similarly to the previous claim, we apply Lemma 11 to find
$j \in [s]$
be given. Similarly to the previous claim, we apply Lemma 11 to find
![]() $y,w \in V^1$
such that
$y,w \in V^1$
such that
![]() $\rho (y,w) = 0$
,
$\rho (y,w) = 0$
,
![]() $\alpha _i(y,w) = 0$
for
$\alpha _i(y,w) = 0$
for
![]() $i \not = j$
and
$i \not = j$
and
![]() $\alpha _j(y,w) = 1$
. Identity (6) for this choice of
$\alpha _j(y,w) = 1$
. Identity (6) for this choice of
![]() $y,w$
and Lemma 7
(iii) show that the rank of the bilinear map
$y,w$
and Lemma 7
(iii) show that the rank of the bilinear map
![]() $\Big (\sum _{i \in [s]}\lambda '_{ij} (\alpha _i|_{V^1 \times V^1}(x,z) + \alpha _i|_{V^1 \times V^1}(z,x))\Big )$
is at most
$\Big (\sum _{i \in [s]}\lambda '_{ij} (\alpha _i|_{V^1 \times V^1}(x,z) + \alpha _i|_{V^1 \times V^1}(z,x))\Big )$
is at most
![]() $2s + 4$
. Lemma 8 provides us with a subspace
$2s + 4$
. Lemma 8 provides us with a subspace
![]() $V^2_j \leq V^1$
with
$V^2_j \leq V^1$
with
![]() $\dim V_j^2 \geq V^1 - 2s - 4$
on which
$\dim V_j^2 \geq V^1 - 2s - 4$
on which
![]() $\sum _{i \in [s]}\lambda '_{ij} \alpha _i$
is symmetric.Footnote
4
To finish the proof, take
$\sum _{i \in [s]}\lambda '_{ij} \alpha _i$
is symmetric.Footnote
4
To finish the proof, take
![]() $V^2 = \cap _{j \in [s]} V^2_j$
.
$V^2 = \cap _{j \in [s]} V^2_j$
.
Proof of (ii). Using the part (i) of Claim 15 we see that whenever
![]() $x,y,z,w \in V^1$
$x,y,z,w \in V^1$
 \begin{align*} & \sum _{i,j \in [s]} (\lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \lambda ''_{ji} \alpha _i(y,x)\alpha _j(z,w)) \\ & \quad = \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} \alpha _i(x,y)\Big ) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda ''_{ji} \alpha _i(y,x)\alpha _j(z,w)\\[5pt] & \quad = \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} \alpha _i(y,x)\Big ) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda ''_{ji} \alpha _i(y,x)\alpha _j(z,w)\\[5pt] & \quad = \sum _{i,j \in [s]} (\lambda _{ij} + \lambda ''_{ji}) \alpha _i(y,x)\alpha _j(z,w). \end{align*}
\begin{align*} & \sum _{i,j \in [s]} (\lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \lambda ''_{ji} \alpha _i(y,x)\alpha _j(z,w)) \\ & \quad = \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} \alpha _i(x,y)\Big ) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda ''_{ji} \alpha _i(y,x)\alpha _j(z,w)\\[5pt] & \quad = \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} \alpha _i(y,x)\Big ) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda ''_{ji} \alpha _i(y,x)\alpha _j(z,w)\\[5pt] & \quad = \sum _{i,j \in [s]} (\lambda _{ij} + \lambda ''_{ji}) \alpha _i(y,x)\alpha _j(z,w). \end{align*}
From (6) we obtain
 \begin{align} 0 &= \sum _{i,j \in [s]} (\lambda _{ij} + \lambda ''_{ji}) \alpha _i(y,x)\alpha _j(z,w) + \sum _{i,j \in [s]} \lambda '_{ij} (\alpha _i(x,z) + \alpha _i(z,x))\alpha _j(y,w) \nonumber \\[5pt] &\quad + \sum _{i,j \in [s]} (\lambda ''_{ij} \alpha _i(x,w) \alpha _j(y,z) + \lambda _{ji} \alpha _i(x,w) \alpha _j(z,y))\nonumber \\[5pt] &\quad +\rho (x,y) (\beta _1(z,w) + \beta _4(z,w)) + \rho (x,w) (\beta _3(y,z) + \beta _6(z,y)) + \rho (y,z) (\beta _4(x,w) + \beta _1(x,w))\nonumber \\[5pt] & \quad + \rho (y,w) (\beta _5(x,z) + \beta _5(z,x)) + \rho (z,w) (\beta _6(x,y) + \beta _3(y,x)) \end{align}
\begin{align} 0 &= \sum _{i,j \in [s]} (\lambda _{ij} + \lambda ''_{ji}) \alpha _i(y,x)\alpha _j(z,w) + \sum _{i,j \in [s]} \lambda '_{ij} (\alpha _i(x,z) + \alpha _i(z,x))\alpha _j(y,w) \nonumber \\[5pt] &\quad + \sum _{i,j \in [s]} (\lambda ''_{ij} \alpha _i(x,w) \alpha _j(y,z) + \lambda _{ji} \alpha _i(x,w) \alpha _j(z,y))\nonumber \\[5pt] &\quad +\rho (x,y) (\beta _1(z,w) + \beta _4(z,w)) + \rho (x,w) (\beta _3(y,z) + \beta _6(z,y)) + \rho (y,z) (\beta _4(x,w) + \beta _1(x,w))\nonumber \\[5pt] & \quad + \rho (y,w) (\beta _5(x,z) + \beta _5(z,x)) + \rho (z,w) (\beta _6(x,y) + \beta _3(y,x)) \end{align}
for all
![]() $x,y,z,w \in V^1$
. We now proceed as in the proof of Claim 15
(ii). Let
$x,y,z,w \in V^1$
. We now proceed as in the proof of Claim 15
(ii). Let
![]() $i, j \in [s]$
be given. Since
$i, j \in [s]$
be given. Since
![]() $m \geq 100(s^2 + s + 1)$
, we may find elements
$m \geq 100(s^2 + s + 1)$
, we may find elements
![]() $x,y,z,w \in V^1$
such that
$x,y,z,w \in V^1$
such that
![]() $\alpha _1, \ldots, \alpha _s$
and
$\alpha _1, \ldots, \alpha _s$
and
![]() $\rho$
are equal to 0 at all 6 points in the set
$\rho$
are equal to 0 at all 6 points in the set
![]() $\{(y,x), (x,z), (x,w), (y,z), (y,w), (z,w)\}$
, with the two exceptions being
$\{(y,x), (x,z), (x,w), (y,z), (y,w), (z,w)\}$
, with the two exceptions being
![]() $\alpha _i(y,x) = \alpha _j(z,w) = 1$
. (Note that this time we use the point
$\alpha _i(y,x) = \alpha _j(z,w) = 1$
. (Note that this time we use the point
![]() $(y,x)$
instead of
$(y,x)$
instead of
![]() $(x,y)$
.) Evaluating (7) at
$(x,y)$
.) Evaluating (7) at
![]() $(x,y,z,w)$
gives
$(x,y,z,w)$
gives
![]() $\lambda _{ij} = \lambda ''_{ji}$
.
$\lambda _{ij} = \lambda ''_{ji}$
.
It remains to use the third symmetry condition
![]() $\phi (x,y,z,w) + \phi (w,y,z,x)= \rho (x,y) \rho (z,w) + \rho (x,z) \rho (y,w)$
.
$\phi (x,y,z,w) + \phi (w,y,z,x)= \rho (x,y) \rho (z,w) + \rho (x,z) \rho (y,w)$
.
Claim 17.
Assume
![]() $m \geq 200(s^2 + s + 1)$
. Then
$m \geq 200(s^2 + s + 1)$
. Then
![]() $\lambda _{ij} = \lambda '_{ji}$
for all
$\lambda _{ij} = \lambda '_{ji}$
for all
![]() $i,j \in [s]$
.
$i,j \in [s]$
.
Proof. The identity
![]() $\phi (x,y,z,w) + \phi (w,y,z,x) = \rho (x,y) \rho (z,w) + \rho (x,z) \rho (y,w)$
implies that
$\phi (x,y,z,w) + \phi (w,y,z,x) = \rho (x,y) \rho (z,w) + \rho (x,z) \rho (y,w)$
implies that
 \begin{align} 0&=\sum _{i,j \in [s]} (\lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \lambda '_{ji} \alpha _i(y,x)\alpha _j(w,z)) + \sum _{i,j \in [s]} (\lambda '_{ij} \alpha _i(x,z) \alpha _j(y,w) + \lambda _{ji} \alpha _i(z,x)\alpha _j(w,y))\nonumber \\[5pt] &\quad + \sum _{i,j \in [s]} \lambda ''_{ij} (\alpha _i(x,w) + \alpha _i(w,x)) \alpha _j(y,z)\nonumber \\[5pt] &\quad +\rho (x,y) (\rho (z,w) + \beta _1(z,w)+ \beta _5(w,z)) + \rho (x,z) (\rho (y,w) + \beta _2(y,w) + \beta _6(w,y))\nonumber \\[5pt] & \quad + \rho (y,z) (\beta _4(x,w) + \beta _4(w,x)) + \rho (y,w) (\beta _5(x,z) + \beta _1(z,x)) + \rho (z,w)(\beta _6(x,y) + \beta _2(y,x)) \end{align}
\begin{align} 0&=\sum _{i,j \in [s]} (\lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \lambda '_{ji} \alpha _i(y,x)\alpha _j(w,z)) + \sum _{i,j \in [s]} (\lambda '_{ij} \alpha _i(x,z) \alpha _j(y,w) + \lambda _{ji} \alpha _i(z,x)\alpha _j(w,y))\nonumber \\[5pt] &\quad + \sum _{i,j \in [s]} \lambda ''_{ij} (\alpha _i(x,w) + \alpha _i(w,x)) \alpha _j(y,z)\nonumber \\[5pt] &\quad +\rho (x,y) (\rho (z,w) + \beta _1(z,w)+ \beta _5(w,z)) + \rho (x,z) (\rho (y,w) + \beta _2(y,w) + \beta _6(w,y))\nonumber \\[5pt] & \quad + \rho (y,z) (\beta _4(x,w) + \beta _4(w,x)) + \rho (y,w) (\beta _5(x,z) + \beta _1(z,x)) + \rho (z,w)(\beta _6(x,y) + \beta _2(y,x)) \end{align}
for all
![]() $x,y,z,w \in U'$
. Using Claims 15
(i) and 16
(i) we see that whenever
$x,y,z,w \in U'$
. Using Claims 15
(i) and 16
(i) we see that whenever
![]() $x,y,z,w \in V^2$
$x,y,z,w \in V^2$
 \begin{align*} \sum _{i,j \in [s]} (\lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) +& \lambda '_{ji} \alpha _i(y,x)\alpha _j(w,z))\\[5pt] = & \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} \alpha _i(x,y)\Big ) \alpha _j(z,w) + \sum _{i \in [s]} \alpha _i(y,x)\Big (\sum _{j \in [s]}\lambda '_{ji} \alpha _j(w,z)\Big )\\[5pt] = & \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} \alpha _i(y,x)\Big ) \alpha _j(z,w) + \sum _{i \in [s]} \alpha _i(y,x)\Big (\sum _{j \in [s]}\lambda '_{ji} \alpha _j(z,w)\Big )\\[5pt] = &\sum _{i,j \in [s]} (\lambda _{ij} + \lambda '_{ji}) \alpha _i(y,x)\alpha _j(z,w). \end{align*}
\begin{align*} \sum _{i,j \in [s]} (\lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) +& \lambda '_{ji} \alpha _i(y,x)\alpha _j(w,z))\\[5pt] = & \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} \alpha _i(x,y)\Big ) \alpha _j(z,w) + \sum _{i \in [s]} \alpha _i(y,x)\Big (\sum _{j \in [s]}\lambda '_{ji} \alpha _j(w,z)\Big )\\[5pt] = & \sum _{j \in [s]} \Big (\sum _{i \in [s]} \lambda _{ij} \alpha _i(y,x)\Big ) \alpha _j(z,w) + \sum _{i \in [s]} \alpha _i(y,x)\Big (\sum _{j \in [s]}\lambda '_{ji} \alpha _j(z,w)\Big )\\[5pt] = &\sum _{i,j \in [s]} (\lambda _{ij} + \lambda '_{ji}) \alpha _i(y,x)\alpha _j(z,w). \end{align*}
Using this identity twice, once with the same choice of variables and once with
![]() $y,z$
swapped, the expression in (8) becomes
$y,z$
swapped, the expression in (8) becomes
 \begin{align*} 0&=\sum _{i,j \in [s]} (\lambda _{ij} + \lambda '_{ji}) \alpha _i(y,x)\alpha _j(z,w) + \sum _{i,j \in [s]} (\lambda '_{ij} + \lambda _{ji}) \alpha _i(z,x)\alpha _j(y,w) \\[5pt] & \quad + \sum _{i,j \in [s]} \lambda ''_{ij} (\alpha _i(x,w) + \alpha _i(w,x)) \alpha _j(y,z)\nonumber \\[5pt] &\quad +\rho (x,y) (\rho (z,w) + \beta _1(z,w)+ \beta _5(w,z)) + \rho (x,z) (\rho (y,w) + \beta _2(y,w) + \beta _6(w,y))\nonumber \\[5pt] &\quad + \rho (y,z) (\beta _4(x,w) + \beta _4(w,x)) + \rho (y,w) (\beta _5(x,z) + \beta _1(z,x)) + \rho (z,w)(\beta _6(x,y) + \beta _2(y,x)) \end{align*}
\begin{align*} 0&=\sum _{i,j \in [s]} (\lambda _{ij} + \lambda '_{ji}) \alpha _i(y,x)\alpha _j(z,w) + \sum _{i,j \in [s]} (\lambda '_{ij} + \lambda _{ji}) \alpha _i(z,x)\alpha _j(y,w) \\[5pt] & \quad + \sum _{i,j \in [s]} \lambda ''_{ij} (\alpha _i(x,w) + \alpha _i(w,x)) \alpha _j(y,z)\nonumber \\[5pt] &\quad +\rho (x,y) (\rho (z,w) + \beta _1(z,w)+ \beta _5(w,z)) + \rho (x,z) (\rho (y,w) + \beta _2(y,w) + \beta _6(w,y))\nonumber \\[5pt] &\quad + \rho (y,z) (\beta _4(x,w) + \beta _4(w,x)) + \rho (y,w) (\beta _5(x,z) + \beta _1(z,x)) + \rho (z,w)(\beta _6(x,y) + \beta _2(y,x)) \end{align*}
for all
![]() $x,y,z,w \in V^2$
. Let
$x,y,z,w \in V^2$
. Let
![]() $i,j \in [s]$
be fixed now. We complete the argument as in the proofs of the previous two claims. Since
$i,j \in [s]$
be fixed now. We complete the argument as in the proofs of the previous two claims. Since
![]() $m$
is sufficiently large, using Lemma 11 we may find elements
$m$
is sufficiently large, using Lemma 11 we may find elements
![]() $x,y,z,w \in V^2$
such that
$x,y,z,w \in V^2$
such that
![]() $\alpha _1, \ldots, \alpha _s$
and
$\alpha _1, \ldots, \alpha _s$
and
![]() $\rho$
are equal to 0 at all 6 points in the set
$\rho$
are equal to 0 at all 6 points in the set
![]() $\{(y,x), (z,x), (w,x), (y,z), (y,w), (z,w)\}$
, with the two exceptions being
$\{(y,x), (z,x), (w,x), (y,z), (y,w), (z,w)\}$
, with the two exceptions being
![]() $\alpha _i(y,x) = \alpha _j(z,w) = 1$
. It follows that
$\alpha _i(y,x) = \alpha _j(z,w) = 1$
. It follows that
![]() $\lambda _{ij} = \lambda '_{ji}$
, as required.
$\lambda _{ij} = \lambda '_{ji}$
, as required.
It follows from Claims 15 (ii), 16 (ii) and 17 that
so
![]() $\lambda _{ij} = \lambda '_{ij} = \lambda ''_{ij}$
and
$\lambda _{ij} = \lambda '_{ij} = \lambda ''_{ij}$
and
![]() $\lambda$
is symmetric. Thus, returning to equality (4) we see that whenever
$\lambda$
is symmetric. Thus, returning to equality (4) we see that whenever
![]() $x,y,z,w \in U'$
then
$x,y,z,w \in U'$
then
 \begin{align*} \phi (x,y,z,w) = \sigma (x,y,z,w) + \psi (x,y,z,w) &+ \rho (x,y) \beta _1(z,w) + \rho (x,z) \beta _2(y,w) + \rho (x,w) \beta _3(y,z) \\[5pt]& + \rho (y,z) \beta _4(x,w) + \rho (y,w) \beta _5(x,z) + \rho (z,w) \beta _6(x,y) \end{align*}
\begin{align*} \phi (x,y,z,w) = \sigma (x,y,z,w) + \psi (x,y,z,w) &+ \rho (x,y) \beta _1(z,w) + \rho (x,z) \beta _2(y,w) + \rho (x,w) \beta _3(y,z) \\[5pt]& + \rho (y,z) \beta _4(x,w) + \rho (y,w) \beta _5(x,z) + \rho (z,w) \beta _6(x,y) \end{align*}
where
![]() $\psi \colon U' \times U' \times U' \times U' \to \mathbb{F}_2$
is the multilinear form defined as
$\psi \colon U' \times U' \times U' \times U' \to \mathbb{F}_2$
is the multilinear form defined as
Claim 18.
Multilinear form
![]() $\psi |_{V^1 \times V^1 \times V^1 \times V^1}$
is symmetric.
$\psi |_{V^1 \times V^1 \times V^1 \times V^1}$
is symmetric.
Proof. Before we proceed with the proof, we observe a few useful identities that hold for any
![]() $a,b,c,d \in V^1$
. Using Claim 15
(ii) and the fact that
$a,b,c,d \in V^1$
. Using Claim 15
(ii) and the fact that
![]() $\lambda$
is symmetric we have
$\lambda$
is symmetric we have
 \begin{eqnarray}{\sum }_{i,j{\in } [s]}{\lambda }_{ij}{\alpha }_i(a,b){\alpha }_j(c,d) ={\sum }_{j \in [s]} \left ({\sum }_{i{\in } [s]}{\lambda }_{ij}{\alpha }_i(a,b)\right ){\alpha }_j(c,d) &=& \sum _{j \in [s]} \left (\sum _{i \in [s]} \lambda _{ij} \alpha _i(b,a)\right ) \alpha _j(c,d)\nonumber \\[5pt] &=&{\sum }_{i,j{\in } [s]}{\lambda }_{ij}{\alpha }_i(b,a){\alpha }_j(c,d) \end{eqnarray}
\begin{eqnarray}{\sum }_{i,j{\in } [s]}{\lambda }_{ij}{\alpha }_i(a,b){\alpha }_j(c,d) ={\sum }_{j \in [s]} \left ({\sum }_{i{\in } [s]}{\lambda }_{ij}{\alpha }_i(a,b)\right ){\alpha }_j(c,d) &=& \sum _{j \in [s]} \left (\sum _{i \in [s]} \lambda _{ij} \alpha _i(b,a)\right ) \alpha _j(c,d)\nonumber \\[5pt] &=&{\sum }_{i,j{\in } [s]}{\lambda }_{ij}{\alpha }_i(b,a){\alpha }_j(c,d) \end{eqnarray}
and
Additionally, from these two identities we deduce
 \begin{eqnarray} \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(a,b)\alpha _j(c,d) &=& \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(c,d)\alpha _j(a,b) = \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(d,c)\alpha _j(a,b) \nonumber \\ &=& \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(a,b)\alpha _j(d,c). \end{eqnarray}
\begin{eqnarray} \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(a,b)\alpha _j(c,d) &=& \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(c,d)\alpha _j(a,b) = \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(d,c)\alpha _j(a,b) \nonumber \\ &=& \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(a,b)\alpha _j(d,c). \end{eqnarray}
Returning to the claim, it suffices to prove
![]() $\psi = \psi \circ (1\,\,2) = \psi \circ (1\,\,3) = \psi \circ (1\,\,4)$
on
$\psi = \psi \circ (1\,\,2) = \psi \circ (1\,\,3) = \psi \circ (1\,\,4)$
on
![]() $V^1 \times V^1 \times V^1 \times V^1$
. Fix
$V^1 \times V^1 \times V^1 \times V^1$
. Fix
![]() $x,y,z,w \in V^1$
. Using the identities (9), (10) and (11) above we obtain
$x,y,z,w \in V^1$
. Using the identities (9), (10) and (11) above we obtain
 \begin{align*} \psi (y,x,z,w) = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,x) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,z) \alpha _j(x,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,w) \alpha _j(x,z)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w)\alpha _j(y,z) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z)\alpha _j(y,w)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y) \alpha _j(z,w)+ \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z)\alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w)\alpha _j(y,z)\\[5pt] = &\; \psi (x, y,z,w). \end{align*}
\begin{align*} \psi (y,x,z,w) = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,x) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,z) \alpha _j(x,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,w) \alpha _j(x,z)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y) \alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w)\alpha _j(y,z) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z)\alpha _j(y,w)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y) \alpha _j(z,w)+ \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z)\alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w)\alpha _j(y,z)\\[5pt] = &\; \psi (x, y,z,w). \end{align*}
Next, we have
 \begin{align*} \psi (z,y,x,w) =&\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,y) \alpha _j(x,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,x) \alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,w) \alpha _j(y,x)\\[5pt] =& \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,z) \alpha _j(x,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z) \alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,w) \alpha _j(x,y)\\[5pt] =&\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w)\alpha _j(y,z) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z) \alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y)\alpha _j(z,w)\\[5pt] =&\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y)\alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z) \alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w)\alpha _j(y,z)\\[5pt] =\; & \psi (x, y,z,w). \end{align*}
\begin{align*} \psi (z,y,x,w) =&\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,y) \alpha _j(x,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,x) \alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,w) \alpha _j(y,x)\\[5pt] =& \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,z) \alpha _j(x,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z) \alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,w) \alpha _j(x,y)\\[5pt] =&\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w)\alpha _j(y,z) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z) \alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y)\alpha _j(z,w)\\[5pt] =&\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y)\alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z) \alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w)\alpha _j(y,z)\\[5pt] =\; & \psi (x, y,z,w). \end{align*}
Finally, we have
 \begin{align*} \psi (w,y,z,x) =&\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(w,y) \alpha _j(z,x) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(w,z) \alpha _j(y,x) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(w,x) \alpha _j(y,z)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,w) \alpha _j(x,z) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,w) \alpha _j(x,y) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w) \alpha _j(y,z)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z)\alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y)\alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w) \alpha _j(y,z)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y)\alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z)\alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w) \alpha _j(y,z)\\[5pt] = &\; \psi (x, y,z,w). \end{align*}
\begin{align*} \psi (w,y,z,x) =&\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(w,y) \alpha _j(z,x) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(w,z) \alpha _j(y,x) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(w,x) \alpha _j(y,z)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(y,w) \alpha _j(x,z) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(z,w) \alpha _j(x,y) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w) \alpha _j(y,z)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z)\alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y)\alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w) \alpha _j(y,z)\\[5pt] = &\sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,y)\alpha _j(z,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,z)\alpha _j(y,w) + \sum _{i,j \in [s]} \lambda _{ij} \alpha _i(x,w) \alpha _j(y,z)\\[5pt] = &\; \psi (x, y,z,w). \end{align*}
Thus, we may consume
![]() $\psi$
into
$\psi$
into
![]() $\sigma$
and without loss of generality
$\sigma$
and without loss of generality
![]() $\phi$
takes the shape
$\phi$
takes the shape
 \begin{eqnarray} \phi (x,y,z,w) = \sigma (x,y,z,w) &+&\rho (x,y) \beta _1(z,w) + \rho (x,z) \beta _2(y,w) + \rho (x,w) \beta _3(y,z)\nonumber \\[5pt] &+&\rho (y,z) \beta _4(x,w) + \rho (y,w) \beta _5(x,z) + \rho (z,w) \beta _6(x,y) \end{eqnarray}
\begin{eqnarray} \phi (x,y,z,w) = \sigma (x,y,z,w) &+&\rho (x,y) \beta _1(z,w) + \rho (x,z) \beta _2(y,w) + \rho (x,w) \beta _3(y,z)\nonumber \\[5pt] &+&\rho (y,z) \beta _4(x,w) + \rho (y,w) \beta _5(x,z) + \rho (z,w) \beta _6(x,y) \end{eqnarray}
for
![]() $x,y,z,w \in V^1$
.
$x,y,z,w \in V^1$
.
We use the symmetry properties of
![]() $\phi$
for the second time in order to elucidate the structure of forms
$\phi$
for the second time in order to elucidate the structure of forms
![]() $\beta _1, \ldots, \beta _6$
. Equality
$\beta _1, \ldots, \beta _6$
. Equality
![]() $\phi = \phi \circ (1\,\,2)$
implies that
$\phi = \phi \circ (1\,\,2)$
implies that
 \begin{align*} 0 &= \phi (x,y,z,w) + \phi (y,x,z,w) \\[5pt] &= \rho (x,z) (\beta _2(y,w) + \beta _4(y,w))+ \rho (x,w) (\beta _3(y,z) + \beta _5(y,z)) + \rho (y,z) (\beta _4(x,w) + \beta _2(x,w))\\[5pt] & \quad + \rho (y,w) (\beta _5(x,z) + \beta _3(x,z)) + \rho (z,w) (\beta _6(x,y) + \beta _6(y,x)) \end{align*}
\begin{align*} 0 &= \phi (x,y,z,w) + \phi (y,x,z,w) \\[5pt] &= \rho (x,z) (\beta _2(y,w) + \beta _4(y,w))+ \rho (x,w) (\beta _3(y,z) + \beta _5(y,z)) + \rho (y,z) (\beta _4(x,w) + \beta _2(x,w))\\[5pt] & \quad + \rho (y,w) (\beta _5(x,z) + \beta _3(x,z)) + \rho (z,w) (\beta _6(x,y) + \beta _6(y,x)) \end{align*}
for
![]() $x,y,z,w \in V^1$
. If we fix
$x,y,z,w \in V^1$
. If we fix
![]() $(z,w) \in V^1 \times V^1$
such that
$(z,w) \in V^1 \times V^1$
such that
![]() $\rho (z,w) = 1$
(such a point exists by Lemma 11 if
$\rho (z,w) = 1$
(such a point exists by Lemma 11 if
![]() $m \geq 100(s^2 + s + 1)$
), we see that the rank of the map
$m \geq 100(s^2 + s + 1)$
), we see that the rank of the map
![]() $(x,y) \mapsto \beta _6(x,y) + \beta _6(y,x)$
on
$(x,y) \mapsto \beta _6(x,y) + \beta _6(y,x)$
on
![]() $V^1 \times V^1$
is at most 4. Similarly, if we fix
$V^1 \times V^1$
is at most 4. Similarly, if we fix
![]() $(x,z) \in V^1 \times V^1$
such that
$(x,z) \in V^1 \times V^1$
such that
![]() $\rho (x,z) = 1$
(respectively
$\rho (x,z) = 1$
(respectively
![]() $(x,w) \in V^1 \times V^1$
such that
$(x,w) \in V^1 \times V^1$
such that
![]() $\rho (x,w) = 1$
), we obtain that the rank of
$\rho (x,w) = 1$
), we obtain that the rank of
![]() $\beta _2 + \beta _4 + \mu \rho$
for scalar
$\beta _2 + \beta _4 + \mu \rho$
for scalar
![]() $\mu = \beta _3(x,z) + \beta _5(x,z)$
(respectively
$\mu = \beta _3(x,z) + \beta _5(x,z)$
(respectively
![]() $\beta _3 + \beta _5 + \mu ' \rho$
for scalar
$\beta _3 + \beta _5 + \mu ' \rho$
for scalar
![]() $\mu ' = \beta _2(x,w) + \beta _4(x,w)$
) is at most 3 on
$\mu ' = \beta _2(x,w) + \beta _4(x,w)$
) is at most 3 on
![]() $V^1 \times V^1$
. Using Lemma 8 we find a suitable subspace
$V^1 \times V^1$
. Using Lemma 8 we find a suitable subspace
![]() $W^1 \leq V^1$
of
$W^1 \leq V^1$
of
![]() $\dim W^1 \geq \dim V^1 - 10$
such that
$\dim W^1 \geq \dim V^1 - 10$
such that
![]() $\beta _6|_{W^1 \times W^1}$
is symmetric and
$\beta _6|_{W^1 \times W^1}$
is symmetric and
Proceeding further, equality
![]() $\phi = \phi \circ (1\,\,3)$
and the fact that
$\phi = \phi \circ (1\,\,3)$
and the fact that
![]() $\beta _6|_{W^1 \times W^1}$
is symmetric imply that for
$\beta _6|_{W^1 \times W^1}$
is symmetric imply that for
![]() $x,y,z,w \in W^1$
we have
$x,y,z,w \in W^1$
we have
 \begin{align*} 0 &= \phi (x,y,z,w) + \phi (z,y,x,w) \\[5pt] &= \rho (x,y) (\beta _1(z,w) + \beta _4(z,w)) + \rho (x,w) (\beta _3(y,z) + \beta _6(z,y)) + \rho (y,z) (\beta _4(x,w) + \beta _1(x,w))\\[5pt] & \quad + \rho (y,w) (\beta _5(x,z) + \beta _5(z,x)) + \rho (z,w) (\beta _6(x,y) + \beta _3(y,x))\\[5pt] & = \rho (x,y) (\beta _1(z,w) + \beta _4(z,w)) + \rho (x,w) (\beta _3(y,z) + \beta _6(y,z)) + \rho (y,z) (\beta _4(x,w) + \beta _1(x,w))\\[5pt] & \quad + \rho (y,w) (\beta _5(x,z) + \beta _5(z,x)) + \rho (z,w) (\beta _6(x,y) + \beta _3(y,x)). \end{align*}
\begin{align*} 0 &= \phi (x,y,z,w) + \phi (z,y,x,w) \\[5pt] &= \rho (x,y) (\beta _1(z,w) + \beta _4(z,w)) + \rho (x,w) (\beta _3(y,z) + \beta _6(z,y)) + \rho (y,z) (\beta _4(x,w) + \beta _1(x,w))\\[5pt] & \quad + \rho (y,w) (\beta _5(x,z) + \beta _5(z,x)) + \rho (z,w) (\beta _6(x,y) + \beta _3(y,x))\\[5pt] & = \rho (x,y) (\beta _1(z,w) + \beta _4(z,w)) + \rho (x,w) (\beta _3(y,z) + \beta _6(y,z)) + \rho (y,z) (\beta _4(x,w) + \beta _1(x,w))\\[5pt] & \quad + \rho (y,w) (\beta _5(x,z) + \beta _5(z,x)) + \rho (z,w) (\beta _6(x,y) + \beta _3(y,x)). \end{align*}
Again, fixing suitable pairs of
![]() $x,y,z,w \in W^1$
with
$x,y,z,w \in W^1$
with
![]() $\rho = 1$
(using Lemma 11, assuming
$\rho = 1$
(using Lemma 11, assuming
![]() $m \geq 200(s^2 + s + 1)$
), we see that the ranks of
$m \geq 200(s^2 + s + 1)$
), we see that the ranks of
![]() $(x,z) \mapsto \beta _5(x,z) + \beta _5(z,x)$
,
$(x,z) \mapsto \beta _5(x,z) + \beta _5(z,x)$
,
![]() $\beta _1 + \beta _4 + \mu \rho$
and
$\beta _1 + \beta _4 + \mu \rho$
and
![]() $\beta _3 + \beta _6 + \mu '\rho$
for suitable scalars
$\beta _3 + \beta _6 + \mu '\rho$
for suitable scalars
![]() $\mu, \mu ' \in \mathbb{F}_2$
are at most 4,3 and 3 respectively. After passing to a suitable subspace
$\mu, \mu ' \in \mathbb{F}_2$
are at most 4,3 and 3 respectively. After passing to a suitable subspace
![]() $W^2 \leq W^1$
of
$W^2 \leq W^1$
of
![]() $\dim W^2 \geq \dim W^1 - 10$
using Lemma 8, we obtain that
$\dim W^2 \geq \dim W^1 - 10$
using Lemma 8, we obtain that
![]() $\beta _5|_{W^2 \times W^2}$
is symmetric and
$\beta _5|_{W^2 \times W^2}$
is symmetric and
Finally, equality
![]() $\phi (x,y,z,w) = \phi (w,y,z,x) + \rho (x,y) \rho (z,w) + \rho (x,z) \rho (y,w)$
and symmetry of maps
$\phi (x,y,z,w) = \phi (w,y,z,x) + \rho (x,y) \rho (z,w) + \rho (x,z) \rho (y,w)$
and symmetry of maps
![]() $\beta _6|_{W^2 \times W^2}$
and
$\beta _6|_{W^2 \times W^2}$
and
![]() $\beta _5|_{W^2 \times W^2}$
give
$\beta _5|_{W^2 \times W^2}$
give
 \begin{align*} &\rho (x,y) \rho (z,w) + \rho (x,z) \rho (y,w) = \phi (x,y,z,w) + \phi (w,y,z,x)\\[5pt] &=\rho (x,y) (\beta _1(z,w) + \beta _5(w,z)) + \rho (x,z)(\beta _2(y,w)+\beta _6(w,y)) + \rho (y,z)(\beta _4(x,w) + \beta _4(w,x))\\[5pt] &+ \rho (y,w) (\beta _5(x,z) + \beta _1(z, x)) + \rho (z,w) (\beta _6(x,y) + \beta _2(y,x))\\[5pt] &=\rho (x,y) (\beta _1(z,w) + \beta _5(z,w)) + \rho (x,z)(\beta _2(y,w)+\beta _6(y,w)) + \rho (y,z)(\beta _4(x,w) + \beta _4(w,x))\\[5pt] &+ \rho (y,w) (\beta _5(z,x) + \beta _1(z, x)) + \rho (z,w) (\beta _6(y,x) + \beta _2(y,x)) \end{align*}
\begin{align*} &\rho (x,y) \rho (z,w) + \rho (x,z) \rho (y,w) = \phi (x,y,z,w) + \phi (w,y,z,x)\\[5pt] &=\rho (x,y) (\beta _1(z,w) + \beta _5(w,z)) + \rho (x,z)(\beta _2(y,w)+\beta _6(w,y)) + \rho (y,z)(\beta _4(x,w) + \beta _4(w,x))\\[5pt] &+ \rho (y,w) (\beta _5(x,z) + \beta _1(z, x)) + \rho (z,w) (\beta _6(x,y) + \beta _2(y,x))\\[5pt] &=\rho (x,y) (\beta _1(z,w) + \beta _5(z,w)) + \rho (x,z)(\beta _2(y,w)+\beta _6(y,w)) + \rho (y,z)(\beta _4(x,w) + \beta _4(w,x))\\[5pt] &+ \rho (y,w) (\beta _5(z,x) + \beta _1(z, x)) + \rho (z,w) (\beta _6(y,x) + \beta _2(y,x)) \end{align*}
for all
![]() $x,y,z,w \in W^2$
. Applying the same argument for the third time, after fixing suitable pairs of
$x,y,z,w \in W^2$
. Applying the same argument for the third time, after fixing suitable pairs of
![]() $x,y,z,w \in W^1$
with
$x,y,z,w \in W^1$
with
![]() $\rho = 1$
(using Lemma 11, this time assuming
$\rho = 1$
(using Lemma 11, this time assuming
![]() $m \geq 300(s^2 + s + 1)$
) we see that the ranks of
$m \geq 300(s^2 + s + 1)$
) we see that the ranks of
![]() $(x,w) \mapsto \beta _4(x,w) + \beta _4(w,x)$
,
$(x,w) \mapsto \beta _4(x,w) + \beta _4(w,x)$
,
![]() $\beta _1 + \beta _5 + \mu \rho$
and
$\beta _1 + \beta _5 + \mu \rho$
and
![]() $\beta _2 + \beta _6 + \mu '\rho$
for suitable scalars
$\beta _2 + \beta _6 + \mu '\rho$
for suitable scalars
![]() $\mu, \mu ' \in \mathbb{F}_2$
are at most 6,4 and 4 respectively. We thus find a subspace
$\mu, \mu ' \in \mathbb{F}_2$
are at most 6,4 and 4 respectively. We thus find a subspace
![]() $W^3 \leq W^2$
of
$W^3 \leq W^2$
of
![]() $\dim W^3 \geq \dim W^2 - 14$
using Lemma 8, such that
$\dim W^3 \geq \dim W^2 - 14$
using Lemma 8, such that
![]() $\beta _4|_{W^3 \times W^3}$
is symmetric and
$\beta _4|_{W^3 \times W^3}$
is symmetric and
Using facts (13), (14) and (15), writing
![]() $\beta = \beta _6$
and restricting all maps to the product
$\beta = \beta _6$
and restricting all maps to the product
![]() $W^3 \times W^3$
, we obtain
$W^3 \times W^3$
, we obtain
![]() $\beta _2, \beta _3 \in \beta + \langle \rho \rangle$
, from which we further get
$\beta _2, \beta _3 \in \beta + \langle \rho \rangle$
, from which we further get
![]() $\beta _4 \in \beta _2 + \langle \rho \rangle = \beta + \langle \rho \rangle$
and
$\beta _4 \in \beta _2 + \langle \rho \rangle = \beta + \langle \rho \rangle$
and
![]() $\beta _5 \in \beta _3 + \langle \rho \rangle = \beta + \langle \rho \rangle$
, which finally implies
$\beta _5 \in \beta _3 + \langle \rho \rangle = \beta + \langle \rho \rangle$
, which finally implies
![]() $\beta _1 \in \beta _4 + \langle \rho \rangle = \beta + \langle \rho \rangle$
. Hence, all
$\beta _1 \in \beta _4 + \langle \rho \rangle = \beta + \langle \rho \rangle$
. Hence, all
![]() $\beta _i$
belong to
$\beta _i$
belong to
![]() $\beta + \langle \rho \rangle$
. In conclusion, we obtain scalars
$\beta + \langle \rho \rangle$
. In conclusion, we obtain scalars
![]() $\lambda _1, \lambda _2, \lambda _3 \in \mathbb{F}_2$
such that
$\lambda _1, \lambda _2, \lambda _3 \in \mathbb{F}_2$
such that
 \begin{align*} \phi (x,y,z,w) = \sigma (x,y,z,w) + &\rho (x,y) \beta (z,w) + \rho (x,z) \beta (y,w) + \rho (x,w) \beta (y,z)\\[5pt] + &\rho (y,z) \beta (x,w) + \rho (y,w) \beta (x,z) + \rho (z,w) \beta (x,y)\\[5pt] + &\lambda _1\rho (x,y)\rho (z,w) + \lambda _2\rho (x,z)\rho (y,w) + \lambda _3\rho (x,w)\rho (y,z) \end{align*}
\begin{align*} \phi (x,y,z,w) = \sigma (x,y,z,w) + &\rho (x,y) \beta (z,w) + \rho (x,z) \beta (y,w) + \rho (x,w) \beta (y,z)\\[5pt] + &\rho (y,z) \beta (x,w) + \rho (y,w) \beta (x,z) + \rho (z,w) \beta (x,y)\\[5pt] + &\lambda _1\rho (x,y)\rho (z,w) + \lambda _2\rho (x,z)\rho (y,w) + \lambda _3\rho (x,w)\rho (y,z) \end{align*}
holds for all
![]() $x,y,z,w \in W^3$
.
$x,y,z,w \in W^3$
.
Since
![]() $\rho$
and
$\rho$
and
![]() $\beta$
are symmetric on
$\beta$
are symmetric on
![]() $W^3 \times W^3$
, the multilinear form
$W^3 \times W^3$
, the multilinear form
is readily seen to be symmetric, so it can be consumed into
![]() $\sigma$
, and on
$\sigma$
, and on
![]() $W^3 \times W^3 \times W^3 \times W^3$
we may assume that
$W^3 \times W^3 \times W^3 \times W^3$
we may assume that
Let us use the symmetry conditions for
![]() $\phi$
for the final time in order to understand the relationship between scalars
$\phi$
for the final time in order to understand the relationship between scalars
![]() $\lambda _1, \lambda _2$
and
$\lambda _1, \lambda _2$
and
![]() $\lambda _3$
. Note that the codimension of the subspace
$\lambda _3$
. Note that the codimension of the subspace
![]() $W^3$
inside
$W^3$
inside
![]() $U'$
is at most
$U'$
is at most
![]() $2s^2 + 5s + 30$
, so by Lemma 9 we have
$2s^2 + 5s + 30$
, so by Lemma 9 we have
![]() $\textrm{rank} \rho |_{W^3 \times W^3} \geq 2$
(assuming
$\textrm{rank} \rho |_{W^3 \times W^3} \geq 2$
(assuming
![]() $m \geq 100(s^2 + s+ 1)$
). The equality
$m \geq 100(s^2 + s+ 1)$
). The equality
![]() $\phi = \phi \circ (1\,\,2)$
gives
$\phi = \phi \circ (1\,\,2)$
gives
for all
![]() $x,y,z,w \in W^3$
. Since
$x,y,z,w \in W^3$
. Since
![]() $\textrm{rank} \rho |_{W^3 \times W^3} \geq 2$
, the map
$\textrm{rank} \rho |_{W^3 \times W^3} \geq 2$
, the map
![]() $\rho |_{W^3 \times W^3}$
is non-zero, so we can find
$\rho |_{W^3 \times W^3}$
is non-zero, so we can find
![]() $(y,w) \in W^3 \times W^3$
such that
$(y,w) \in W^3 \times W^3$
such that
![]() $\rho (y,w) = 1$
. The equality above then shows that
$\rho (y,w) = 1$
. The equality above then shows that
![]() $(\lambda _2 + \lambda _3)\rho |_{W^3 \times W^3}$
has rank at most 1. However, using the fact that the rank of
$(\lambda _2 + \lambda _3)\rho |_{W^3 \times W^3}$
has rank at most 1. However, using the fact that the rank of
![]() $\rho |_{W^3 \times W^3}$
is at least 2 again, we deduce
$\rho |_{W^3 \times W^3}$
is at least 2 again, we deduce
![]() $\lambda _2 = \lambda _3$
.
$\lambda _2 = \lambda _3$
.
Similarly, the condition
![]() $\phi = \phi \circ (1\,\,3)$
implies
$\phi = \phi \circ (1\,\,3)$
implies
for all
![]() $x,y,z,w \in W^3$
. Using the same rank bound
$x,y,z,w \in W^3$
. Using the same rank bound
![]() $\textrm{rank} \rho |_{W^3 \times W^3} \geq 2$
allows us to deduce
$\textrm{rank} \rho |_{W^3 \times W^3} \geq 2$
allows us to deduce
![]() $\lambda _1 = \lambda _3$
.
$\lambda _1 = \lambda _3$
.
Putting these equalities together we see that
![]() $\lambda _1 = \lambda _2 = \lambda _3$
and equality (16) then becomes
$\lambda _1 = \lambda _2 = \lambda _3$
and equality (16) then becomes
so
![]() $\phi = \phi \circ (1\,\,4)$
on
$\phi = \phi \circ (1\,\,4)$
on
![]() $W^3 \times W^3$
. The third symmetry condition tells us that
$W^3 \times W^3$
. The third symmetry condition tells us that
for all
![]() $x,y,z,w \in W^3$
, which is a contradiction as the rank of
$x,y,z,w \in W^3$
, which is a contradiction as the rank of
![]() $\rho |_{W^3 \times W^3}$
is at least 2. To complete the proof of the theorem it remains to choose
$\rho |_{W^3 \times W^3}$
is at least 2. To complete the proof of the theorem it remains to choose
![]() $m = 20,000(r^2 + r + 1)$
(recall that
$m = 20,000(r^2 + r + 1)$
(recall that
![]() $s \leq 6r$
) so that all conditions on
$s \leq 6r$
) so that all conditions on
![]() $m$
are satisfied. The assumption
$m$
are satisfied. The assumption
![]() $n \geq (1000r)^3$
in the statement of the theorem then implies the condition (3).
$n \geq (1000r)^3$
in the statement of the theorem then implies the condition (3).
Acknowledgements
This work was supported by the Serbian Ministry of Education, Science and Technological Development through Mathematical Institute of the Serbian Academy of Sciences and Arts. I would like to thank an anonymous referee for a thorough reading of the paper and numerous useful suggestions.