Article contents
Universality of Graphs with Few Triangles and Anti-Triangles
Published online by Cambridge University Press: 29 July 2015
Abstract
We study 3-random-like graphs, that is, sequences of graphs in which the densities of triangles and anti-triangles converge to 1/8. Since the random graph 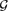 $\mathcal{G}$n,1/2 is, in particular, 3-random-like, this can be viewed as a weak version of quasi-randomness. We first show that 3-random-like graphs are 4-universal, that is, they contain induced copies of all 4-vertex graphs. This settles a question of Linial and Morgenstern [10]. We then show that for larger subgraphs, 3-random-like sequences demonstrate completely different behaviour. We prove that for every graph H on n ⩾ 13 vertices there exist 3-random-like graphs without an induced copy of H. Moreover, we prove that for every ℓ there are 3-random-like graphs which are ℓ-universal but not m-universal when m is sufficiently large compared to ℓ.
$\mathcal{G}$n,1/2 is, in particular, 3-random-like, this can be viewed as a weak version of quasi-randomness. We first show that 3-random-like graphs are 4-universal, that is, they contain induced copies of all 4-vertex graphs. This settles a question of Linial and Morgenstern [10]. We then show that for larger subgraphs, 3-random-like sequences demonstrate completely different behaviour. We prove that for every graph H on n ⩾ 13 vertices there exist 3-random-like graphs without an induced copy of H. Moreover, we prove that for every ℓ there are 3-random-like graphs which are ℓ-universal but not m-universal when m is sufficiently large compared to ℓ.
MSC classification
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2015
References
- 1
- Cited by


