Article contents
On minimal Ramsey graphs and Ramsey equivalence in multiple colours
Published online by Cambridge University Press: 09 March 2020
Abstract
For an integer q ⩾ 2, a graph G is called q-Ramsey for a graph H if every q-colouring of the edges of G contains a monochromatic copy of H. If G is q-Ramsey for H yet no proper subgraph of G has this property, then G is called q-Ramsey-minimal for H. Generalizing a statement by Burr, Nešetřil and Rödl from 1977, we prove that, for q ⩾ 3, if G is a graph that is not q-Ramsey for some graph H, then G is contained as an induced subgraph in an infinite number of q-Ramsey-minimal graphs for H as long as H is 3-connected or isomorphic to the triangle. For such H, the following are some consequences.
For 2 ⩽ r < q, every r-Ramsey-minimal graph for H is contained as an induced subgraph in an infinite number of q-Ramsey-minimal graphs for H.
For every q ⩾ 3, there are q-Ramsey-minimal graphs for H of arbitrarily large maximum degree, genus and chromatic number.
The collection
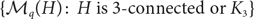 $\{\mathcal M_q(H) \colon H \text{ is 3-connected or } K_3\}$
forms an antichain with respect to the subset relation, where
$\{\mathcal M_q(H) \colon H \text{ is 3-connected or } K_3\}$
forms an antichain with respect to the subset relation, where 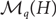 $\mathcal M_q(H)$
denotes the set of all graphs that are q-Ramsey-minimal for H.
$\mathcal M_q(H)$
denotes the set of all graphs that are q-Ramsey-minimal for H.
We also address the question of which pairs of graphs satisfy 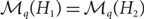 $\mathcal M_q(H_1)=\mathcal M_q(H_2)$
, in which case H1 and H2 are called q-equivalent. We show that two graphs H1 and H2 are q-equivalent for even q if they are 2-equivalent, and that in general q-equivalence for some q ⩾ 3 does not necessarily imply 2-equivalence. Finally we indicate that for connected graphs this implication may hold: results by Nešetřil and Rödl and by Fox, Grinshpun, Liebenau, Person and Szabó imply that the complete graph is not 2-equivalent to any other connected graph. We prove that this is the case for an arbitrary number of colours.
$\mathcal M_q(H_1)=\mathcal M_q(H_2)$
, in which case H1 and H2 are called q-equivalent. We show that two graphs H1 and H2 are q-equivalent for even q if they are 2-equivalent, and that in general q-equivalence for some q ⩾ 3 does not necessarily imply 2-equivalence. Finally we indicate that for connected graphs this implication may hold: results by Nešetřil and Rödl and by Fox, Grinshpun, Liebenau, Person and Szabó imply that the complete graph is not 2-equivalent to any other connected graph. We prove that this is the case for an arbitrary number of colours.
MSC classification
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2020
Footnotes
Supported by an ARC Decra Fellowship. Previously at Monash University where this research was partly carried out.
References
- 4
- Cited by



