Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hoppen, Carlos
Kohayakawa, Yoshiharu
and
Lefmann, Hanno
2012.
Hypergraphs with many Kneser colorings.
European Journal of Combinatorics,
Vol. 33,
Issue. 5,
p.
816.
HOPPEN, CARLOS
KOHAYAKAWA, YOSHIHARU
and
LEFMANN, HANNO
2012.
Edge Colourings of Graphs Avoiding Monochromatic Matchings of a Given Size.
Combinatorics, Probability and Computing,
Vol. 21,
Issue. 1-2,
p.
203.
Lefmann, Hanno
and
Person, Yury
2013.
Exact Results on the Number of Restricted Edge Colorings for Some Families of Linear Hypergraphs.
Journal of Graph Theory,
Vol. 73,
Issue. 1,
p.
1.
Hoppen, Carlos
Kohayakawa, Yoshiharu
and
Lefmann, Hanno
2014.
Edge-colorings of graphs avoiding fixed monochromatic subgraphs with linear Turán number.
European Journal of Combinatorics,
Vol. 35,
Issue. ,
p.
354.
Hoppen, Carlos
Kohayakawa, Yoshiharu
and
Lefmann, Hanno
2015.
Edge-colorings of uniform hypergraphs avoiding monochromatic matchings.
Discrete Mathematics,
Vol. 338,
Issue. 2,
p.
262.
Hoppen, Carlos
and
Lefmann, Hanno
2015.
Edge-colorings avoiding a fixed matching with a prescribed color pattern.
European Journal of Combinatorics,
Vol. 47,
Issue. ,
p.
75.
Hoppen, Carlos
Lefmann, Hanno
and
Odermann, Knut
2016.
A coloring problem for intersecting vector spaces.
Discrete Mathematics,
Vol. 339,
Issue. 12,
p.
2941.
Hoppen, Carlos
Lefmann, Hanno
and
Odermann, Knut
2017.
A Rainbow Erdös--Rothschild Problem.
SIAM Journal on Discrete Mathematics,
Vol. 31,
Issue. 4,
p.
2647.
de Oliveira Contiero, Lucas
Hoppen, Carlos
Lefmann, Hanno
and
Odermann, Knut
2017.
Stability of extremal hypergraphs with applications to an edge-coloring problem.
Electronic Notes in Discrete Mathematics,
Vol. 61,
Issue. ,
p.
263.
PIKHURKO, OLEG
STADEN, KATHERINE
and
YILMA, ZELEALEM B.
2017.
The Erdős–Rothschild problem on edge-colourings with forbidden monochromatic cliques.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 163,
Issue. 2,
p.
341.
Clemens, Dennis
Das, Shagnik
and
Tran, Tuan
2018.
Colourings without monochromatic disjoint pairs.
European Journal of Combinatorics,
Vol. 70,
Issue. ,
p.
99.
Hoppen, Carlos
Lefmann, Hanno
Odermann, Knut
and
Sanches, Juliana
2018.
Edge‐colorings avoiding rainbow stars.
Journal of Graph Theory,
Vol. 87,
Issue. 4,
p.
399.
Hàn, Hiệp
and
Jiménez, Andrea
2018.
Maximum number of sum-free colorings in finite abelian groups.
Israel Journal of Mathematics,
Vol. 226,
Issue. 2,
p.
505.
Das, Shagnik
Glebov, Roman
Sudakov, Benny
and
Tran, Tuan
2019.
Colouring set families without monochromatic k-chains.
Journal of Combinatorial Theory, Series A,
Vol. 168,
Issue. ,
p.
84.
Simonovits, Miklós
and
Szemerédi, Endre
2019.
Building Bridges II.
Vol. 28,
Issue. ,
p.
445.
Contiero, Lucas de Oliveira
Hoppen, Carlos
Lefmann, Hanno
and
Odermann, Knut
2021.
Uniform hypergraphs with many edge‐colorings avoiding a fixed rainbow expanded complete graph.
Journal of Graph Theory,
Vol. 98,
Issue. 1,
p.
141.
de Oliveira Contiero, Lucas
Hoppen, Carlos
Lefmann, Hanno
and
Odermann, Knut
2021.
Rainbow Erdös--Rothschild Problem for the Fano Plane.
SIAM Journal on Discrete Mathematics,
Vol. 35,
Issue. 3,
p.
1927.
Kittipassorn, Teeradej
and
Sirirojrattana, Boonpipop
2022.
Monochromatic Edges in Complete Multipartite Hypergraphs.
Mathematics,
Vol. 10,
Issue. 13,
p.
2353.
BUCIĆ, MATIJA
JANZER, OLIVER
and
SUDAKOV, BENNY
2023.
Counting H-free orientations of graphs.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 174,
Issue. 1,
p.
79.
Cheng, Yangyang
Jing, Yifan
Li, Lina
Wang, Guanghui
and
Zhou, Wenling
2023.
Integer colorings with forbidden rainbow sums.
Journal of Combinatorial Theory, Series A,
Vol. 199,
Issue. ,
p.
105769.
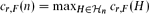 , where the maximum runs over all k-uniform hypergraphs on n vertices. Moreover, let ex(n,F) be the usual extremal or Turán function, i.e., the maximum number of hyperedges of an n-vertex k-uniform hypergraph which contains no copy of F.
, where the maximum runs over all k-uniform hypergraphs on n vertices. Moreover, let ex(n,F) be the usual extremal or Turán function, i.e., the maximum number of hyperedges of an n-vertex k-uniform hypergraph which contains no copy of F.

