Article contents
Lower Bounds for the Cop Number when the Robber is Fast
Published online by Cambridge University Press: 19 April 2011
Abstract
We consider a variant of the Cops and Robbers game where the robber can move t edges at a time, and show that in this variant, the cop number of a d-regular graph with girth larger than 2t+2 is Ω(dt). By the known upper bounds on the order of cages, this implies that the cop number of a connected n-vertex graph can be as large as Ω(n2/3) if t ≥ 2, and Ω(n4/5) if t ≥ 4. This improves the Ω(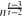 ) lower bound of Frieze, Krivelevich and Loh (Variations on cops and robbers, J. Graph Theory, to appear) when 2 ≤ t ≤ 6. We also conjecture a general upper bound O(nt/t+1) for the cop number in this variant, generalizing Meyniel's conjecture.
) lower bound of Frieze, Krivelevich and Loh (Variations on cops and robbers, J. Graph Theory, to appear) when 2 ≤ t ≤ 6. We also conjecture a general upper bound O(nt/t+1) for the cop number in this variant, generalizing Meyniel's conjecture.
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 6
- Cited by


