No CrossRef data available.
Article contents
Economical Elimination of Cycles in the Torus
Published online by Cambridge University Press: 01 September 2009
Abstract
Let m > 2 be an integer, let C2m denote the cycle of length 2m on the set of vertices [−m, m) = {−m, −m + 1, . . ., m − 2, m − 1}, and let G = G(m, d) denote the graph on the set of vertices [−m, m)d, in which two vertices are adjacent if and only if they are adjacent in C2m in one coordinate, and equal in all others. This graph can be viewed as the graph of the d-dimensional torus. We prove that one can delete a fraction of at most 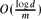 of the vertices of G so that no topologically non-trivial cycles remain. This is tight up to the logd factor and improves earlier estimates by various researchers.
of the vertices of G so that no topologically non-trivial cycles remain. This is tight up to the logd factor and improves earlier estimates by various researchers.
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 18 , Issue 5: New Directions in Algorithms, Combinatorics and Optimization , September 2009 , pp. 619 - 627
- Copyright
- Copyright © Cambridge University Press 2009


