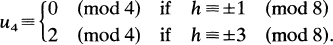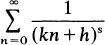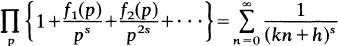Research Article
Some Examples of Smooth and Regular Rings(1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 255-259
-
- Article
-
- You have access
- Export citation
A Function which Transforms Certain Graphs into Straight Lines for Simultaneous Solution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 261-266
-
- Article
-
- You have access
- Export citation
Some Triangle Inequalities and Generalizations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 267-274
-
- Article
-
- You have access
- Export citation
Decomposition of Kn into Dragons
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 275-279
-
- Article
-
- You have access
- Export citation
A New Identity and Some Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 281-290
-
- Article
-
- You have access
- Export citation
On Prime Semilattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 291-298
-
- Article
-
- You have access
- Export citation
Nilpotent Ideals in Alternative Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 299-303
-
- Article
-
- You have access
- Export citation
A Characterisation of Locally Compact Amenable Subsemigroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 305-312
-
- Article
-
- You have access
- Export citation
A Comment on Finite Nilpotent Groups of Deficiency Zero
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 313-316
-
- Article
-
- You have access
- Export citation
Coincidence of Nodes for Generalized Convex Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 317-320
-
- Article
-
- You have access
- Export citation
On the Boundedness and Range of the Extended Hankel Transformation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-325
-
- Article
-
- You have access
- Export citation
On the Number of Zeros Over a Finite Field of Certain Symmetric Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 327-332
-
- Article
-
- You have access
- Export citation
The Ruin Problem for Sums of Dependent Random Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 333-337
-
- Article
-
- You have access
- Export citation
Some Generalizations of Carathéodory′s Theorem Via Barycentres, with Application to Mathematical Programming
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 339-346
-
- Article
-
- You have access
- Export citation
Gaps between Spheres in Normed Linear Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 347-354
-
- Article
-
- You have access
- Export citation
Least Positive Residues and the Quadratic Character of Two
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 355-358
-
- Article
-
- You have access
- Export citation
A Note on the Jensen-Gould Convolutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 359-361
-
- Article
-
- You have access
- Export citation
Complements of Minimal Ideals in Solvable Lie Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 363-366
-
- Article
-
- You have access
- Export citation
A Note on Doubles of 4-Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 367-369
-
- Article
-
- You have access
- Export citation
On the Non-Existence of Certain Euler Products
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 371-372
-
- Article
-
- You have access
- Export citation



 the ring of integers. These results do not seem to be well known, especially those dealing with regularity. At any rate, several of my colleagues knew that
the ring of integers. These results do not seem to be well known, especially those dealing with regularity. At any rate, several of my colleagues knew that  was not smooth, but thought that it might be regular. I was surprised by the number of possibilities that can occur, as well as by the fact that
was not smooth, but thought that it might be regular. I was surprised by the number of possibilities that can occur, as well as by the fact that 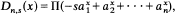 , where
, where 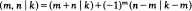
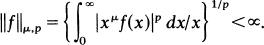
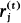 be the least positive residue modulo 2
be the least positive residue modulo 2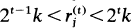 . At the Special Session in Combinatorial Number Theory at the 1977 Summer AMS Meeting Szekeres [2] asked for a simple proof that if (
. At the Special Session in Combinatorial Number Theory at the 1977 Summer AMS Meeting Szekeres [2] asked for a simple proof that if (