Research Article
The Poincaré Map in Mixed Exterior Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-136
-
- Article
-
- You have access
- Export citation
Lp Spaces from Matrix Measures: A Correction and their Interpolation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 137-143
-
- Article
-
- You have access
- Export citation
Covering Problem for Idempotent Latin Squares
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 144-148
-
- Article
-
- You have access
- Export citation
A Typical Nowhere Differentiable Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-151
-
- Article
-
- You have access
- Export citation
On k-Cycled Refinements of Certain Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 152-156
-
- Article
-
- You have access
- Export citation
Embedding Theorems in Group C*-Algebras†
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 157-166
-
- Article
-
- You have access
- Export citation
Coincidence Sets of Coincidence Producing Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 167-170
-
- Article
-
- You have access
- Export citation
Extremal Positive Solutions of Semilinear Schrödinger Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 171-178
-
- Article
-
- You have access
- Export citation
A Regular Summability Method which Sums the Geometric Series to its Proper Value in the Whole Complex Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 179-188
-
- Article
-
- You have access
- Export citation
Hülder Conditions and the Topology of Simply Connected Domains*
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 189-191
-
- Article
-
- You have access
- Export citation
The Maximal Extension of a Zero-dimensional Product Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 192-201
-
- Article
-
- You have access
- Export citation
Coefficient Estimates of Some Classes of Analytic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 202-208
-
- Article
-
- You have access
- Export citation
Sur Les Sous-Groupes Normaux De SL2 Sur Un Anneau Local
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 209-219
-
- Article
-
- You have access
- Export citation
On Comonotone Approximation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 220-224
-
- Article
-
- You have access
- Export citation
q -Analogs of Some Biorthogonal Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-227
-
- Article
-
- You have access
- Export citation
A Note on Locally Expansive and Locally Accretive Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 228-232
-
- Article
-
- You have access
- Export citation
Semigroup Compactifications of Direct and Semidirect Products
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 233-240
-
- Article
-
- You have access
- Export citation
The Second Dual of a C*-Ternary Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-246
-
- Article
-
- You have access
- Export citation
Krasnosel'skii Theorems for Non-Separating Compact Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 247-249
-
- Article
-
- You have access
- Export citation



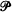 of Tychonoff spaces is closed-hereditary, productive and possessed by all compact Hausdorff spaces, then each (0-dimensional) Tychonoff space X is a dense subspace of a (0-dimensional) Tychonoff space
of Tychonoff spaces is closed-hereditary, productive and possessed by all compact Hausdorff spaces, then each (0-dimensional) Tychonoff space X is a dense subspace of a (0-dimensional) Tychonoff space 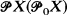 with
with 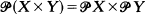 if and only if
if and only if 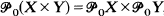 , then
, then 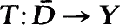 closed, locally
closed, locally