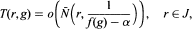Research Article
Similarity of Nests in Lp, 1 ≤ p ≠ 2 < ∞
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-389
-
- Article
-
- You have access
- Export citation
A Note on Geometric Factoriality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 390-395
-
- Article
-
- You have access
- Export citation
CR Mappings of Circular CR Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 396-407
-
- Article
-
- You have access
- Export citation
Stably Free Modules Over Rings of Generalised Integer Quaternions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 408-411
-
- Article
-
- You have access
- Export citation
Connectedness of the Invertibles in Certain Nest Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 412-420
-
- Article
-
- You have access
- Export citation
Quasi-Hereditary Endomorphism Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 421-428
-
- Article
-
- You have access
- Export citation
Weak Normalization of Power Series Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 429-433
-
- Article
-
- You have access
- Export citation
A Note on Derivations of Group Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 434-437
-
- Article
-
- You have access
- Export citation
Comparaison de Deux Mesures de Polynômes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 438-444
-
- Article
-
- You have access
- Export citation
Semiprime Rings with Hypercentral Derivations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 445-449
-
- Article
-
- You have access
- Export citation
Award Winners
Research Article
A Note on the Relative Trace Formula
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 450-461
-
- Article
-
- You have access
- Export citation
Research Article
The Genus of the Coxeter Graph
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 462-464
-
- Article
-
- You have access
- Export citation
On Minimal Sets of Generators for Primitive Roots
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 465-468
-
- Article
-
- You have access
- Export citation
Cut and Paste in 2-Dimensional Projective Planes and Circle Planes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 469-480
-
- Article
-
- You have access
- Export citation
α-Derivations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-489
-
- Article
-
- You have access
- Export citation
A Quantitative Estimate on Fixed-Points of Composite Meromorphic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 490-495
-
- Article
-
- You have access
- Export citation
Definitizable Operators on a Krein Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 496-506
-
- Article
-
- You have access
- Export citation



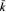 is solvable over
is solvable over 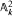 is geometrically factorial and hence isomorphic to
is geometrically factorial and hence isomorphic to 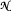 is a nest with no isolated atoms of finite multiplicity, then the invertibles in
is a nest with no isolated atoms of finite multiplicity, then the invertibles in 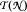 are connected. The key technical ingredient is that in such nest algebras, every operator with zero atomic diagonal part factors through the non-atomic part of
are connected. The key technical ingredient is that in such nest algebras, every operator with zero atomic diagonal part factors through the non-atomic part of