Article contents
Ternary Quadratic Forms and Eta Quotients
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 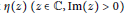 $\eta \left( z \right)\,\left( z\,\in \,\mathbb{C},\,\operatorname{Im}\left( z \right)\,>\,0 \right)$ denote the Dedekind eta function. We use a recent product-to-sum formula in conjunction with conditions for the non-representability of integers by certain
ternary quadratic forms to give explicitly ten eta quotients
$\eta \left( z \right)\,\left( z\,\in \,\mathbb{C},\,\operatorname{Im}\left( z \right)\,>\,0 \right)$ denote the Dedekind eta function. We use a recent product-to-sum formula in conjunction with conditions for the non-representability of integers by certain
ternary quadratic forms to give explicitly ten eta quotients
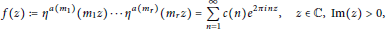 $$f\left( z \right)\,:=\,{{\eta }^{a\left( {{m}_{1}} \right)}}\,\left( {{m}_{1}}z \right)\,.\,.\,.\,{{\eta }^{a\left( {{m}_{r}} \right)}}\,\left( {{m}_{r}}z \right)\,=\,\sum\limits_{n=1}^{\infty }{c\left( n \right){{e}^{2\pi inz}},\,\,\,z\,\in \,\mathbb{C},\,\operatorname{Im}\left( z \right)\,>\,0,}$$
$$f\left( z \right)\,:=\,{{\eta }^{a\left( {{m}_{1}} \right)}}\,\left( {{m}_{1}}z \right)\,.\,.\,.\,{{\eta }^{a\left( {{m}_{r}} \right)}}\,\left( {{m}_{r}}z \right)\,=\,\sum\limits_{n=1}^{\infty }{c\left( n \right){{e}^{2\pi inz}},\,\,\,z\,\in \,\mathbb{C},\,\operatorname{Im}\left( z \right)\,>\,0,}$$
such that the Fourier coefficients 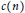 $c\left( n \right)$ vanish for all positive integers
$c\left( n \right)$ vanish for all positive integers  $n$ in each of infinitely many non-overlapping arithmetic progressions. For example, we show that if
$n$ in each of infinitely many non-overlapping arithmetic progressions. For example, we show that if 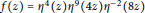 $f\left( z \right)\,=\,{{\eta }^{4}}\left( z \right){{\eta }^{9}}\left( 4z \right){{\eta }^{-2}}\left( 8z \right)$ we have
$f\left( z \right)\,=\,{{\eta }^{4}}\left( z \right){{\eta }^{9}}\left( 4z \right){{\eta }^{-2}}\left( 8z \right)$ we have 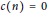 $c\left( n \right)\,=\,0$ for all
$c\left( n \right)\,=\,0$ for all  $n$ in each of the arithmetic progressions
$n$ in each of the arithmetic progressions 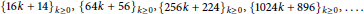 ${{\{16k\,+\,14\}}_{k\ge 0}},\,{{\{64k\,+\,56\}}_{k\ge 0}},\,{{\{256k,\,224\}}_{k\ge 0}},\,{{\{1024k\,+\,869\}}_{k\ge 0}},\,.\,.\,.$
${{\{16k\,+\,14\}}_{k\ge 0}},\,{{\{64k\,+\,56\}}_{k\ge 0}},\,{{\{256k,\,224\}}_{k\ge 0}},\,{{\{1024k\,+\,869\}}_{k\ge 0}},\,.\,.\,.$
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
- 2
- Cited by




