Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2025-01-02T23:54:51.187Z Has data issue: false hasContentIssue false
  • English
  • Français

A parametrization of sheets of conjugacy classes in bad characteristic

Part of: Structure and classification of infinite or finite groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  26 January 2023

Filippo Ambrosio Open the ORCID record for Filippo Ambrosio [Opens in a new window] ,
Giovanna Carnovale Open the ORCID record for Giovanna Carnovale [Opens in a new window]  and
Francesco Esposito
Filippo Ambrosio
Affiliation:
Dipartimento di Matematica “Tullio Levi-Civita”, Università di Padova, via Trieste 63, 35121 Padova, Italy e-mail: ambrosio@math.unipd.it esposito@math.unipd.it
Giovanna Carnovale*
Affiliation:
Dipartimento di Matematica “Tullio Levi-Civita”, Università di Padova, via Trieste 63, 35121 Padova, Italy e-mail: ambrosio@math.unipd.it esposito@math.unipd.it
Francesco Esposito
Affiliation:
Dipartimento di Matematica “Tullio Levi-Civita”, Università di Padova, via Trieste 63, 35121 Padova, Italy e-mail: ambrosio@math.unipd.it esposito@math.unipd.it
*
e-mail: carnoval@math.unipd.it
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a simple algebraic group of adjoint type over an algebraically closed field k of bad characteristic. We show that its sheets of conjugacy classes are parametrized by G-conjugacy classes of pairs 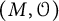$(M,{\mathcal O})$ where M is the identity component of the centralizer of a semisimple element in G and 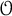${\mathcal O}$ is a rigid unipotent conjugacy class in M, in analogy with the good characteristic case.

Keywords

Reductive algebraic groupsconjugacy classessheetsbad characteristic

MSC classification

Primary: 20G15: Linear algebraic groups over arbitrary fields
Secondary: 20E45: Conjugacy classes
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 3 , September 2023 , pp. 976 - 983
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors acknowledge support by: DOR2207212/22 “Algebre di Nichols, algebre di Hopf e gruppi algebrici” and BIRD203834 “Grassmannians, flag varieties and their generalizations” funded by the University of Padova. They are members of the INdAM group GNSAGA.

References

Bourbaki, N., Groupes et Algèbres de lie, Chapitres 4,5, et 6, Éléments de Mathématique, Masson, Paris, 1981.Google Scholar
Carnovale, G., Lusztig’s partition and sheets (with an appendix by M. Bulois) . Math. Res. Lett. 22(2015), 645–664.CrossRefGoogle Scholar
Carnovale, G., Lusztig’s strata are locally closed . Arch. Math. 115(2020), 23–26.CrossRefGoogle Scholar
Carnovale, G. and Esposito, F., On sheets of conjugacy classes in good characteristic . Int. Math. Res. Not. 4(2012), 810–828.CrossRefGoogle Scholar
Carter, R. W., Centralizers of semisimple elements in finite groups of lie type . Proc. Lond. Math. Soc. 37(1978), no. 3, 491–507.CrossRefGoogle Scholar
Carter, R. W., Centralizers of semisimple elements in the finite classical groups . Proc. Lond. Math. Soc. 42(1981), 1–41.CrossRefGoogle Scholar
Deriziotis, D. I., The Brauer complex and its applications to the Chevalley groups. Ph.D. thesis, University of Warwick, 1977.Google Scholar
Deriziotis, D. I., Centralizers of semisimple elements in a Chevalley group . Comm. Algebra 9(1981), no. 19, 1997–2014.CrossRefGoogle Scholar
Lusztig, G., Intersection cohomology complexes on a reductive group . Invent. Math. 75(1984), 205–272.CrossRefGoogle Scholar
Lusztig, G., On conjugacy classes in a reductive group . In: Nevins, M. and Trapa, P. (eds.), Representations of reductive groups, Progress in Mathematics, 312, Springer, Cham, 2015, pp. 333–363.CrossRefGoogle Scholar
Lusztig, G. and Spaltenstein, N., Induced unipotent classes . J. Lond. Math. Soc. (2) 19(1979), 41–52.CrossRefGoogle Scholar
Malle, G. and Testerman, D., Linear algebraic groups and finite groups of lie type, Cambridge Studies in Advanced Mathematics, 133, Cambridge University Press, Cambridge, 2011.CrossRefGoogle Scholar
McNinch, G. and Sommers, E., Component groups of unipotent centralizers in good characteristic . J. Algebra 270(2003), no. 1, 288–306.Google Scholar
Simion, I., Sheets of conjugacy classes in simple algebraic groups . Mathematica 61(2019), no. 84, 183–190.CrossRefGoogle Scholar
Sommers, E., A generalization of the Bala–Carter theorem for nilpotent orbits . Int. Math. Res. Not. 11(1998), 539–562.CrossRefGoogle Scholar
Spaltenstein, N., Classes unipotentes et sous-groupes de Borel, Lecture Notes in Mathematics, 946, Springer, Cham, 1982.CrossRefGoogle Scholar