Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-18T18:13:21.504Z Has data issue: false hasContentIssue false
  • English
  • Français

On Motivic Realizations of the Canonical Hermitian Variations of Hodge Structure of Calabi–Yau Type over type 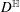$D^{\mathbb{H}}$ Domains

Part of: Automorphic functions Complex spaces with a group of automorphisms Families, fibrations Deformations of analytic structures

Published online by Cambridge University Press:  04 January 2019

Zheng Zhang
Zheng Zhang*
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX 77843-3368, USA Email: zzhang@math.tamu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 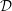${\mathcal{D}}$ be the irreducible Hermitian symmetric domain of type 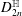$D_{2n}^{\mathbb{H}}$. There exists a canonical Hermitian variation of real Hodge structure 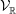${\mathcal{V}}_{\mathbb{R}}$ of Calabi–Yau type over ${\mathcal{D}}$. This short note concerns the problem of giving motivic realizations for 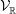${\mathcal{V}}_{\mathbb{R}}$. Namely, we specify a descent of 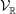${\mathcal{V}}_{\mathbb{R}}$ from 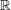$\mathbb{R}$ to 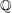$\mathbb{Q}$ and ask whether the 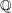$\mathbb{Q}$-descent of 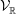${\mathcal{V}}_{\mathbb{R}}$ can be realized as sub-variation of rational Hodge structure of those coming from families of algebraic varieties. When 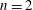$n=2$, we give a motivic realization for 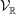${\mathcal{V}}_{\mathbb{R}}$. When $n\geqslant 3$, we show that the unique irreducible factor of Calabi–Yau type in 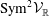$\text{Sym}^{2}{\mathcal{V}}_{\mathbb{R}}$ can be realized motivically.

Keywords

variations of Hodge structureHermitian symmetric domain

MSC classification

Primary: 14D07: Variation of Hodge structures
Secondary: 32G20: Period matrices, variation of Hodge structure; degenerations 32M15: Hermitian symmetric spaces, bounded symmetric domains, Jordan algebras
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 1 , March 2019 , pp. 209 - 221
Copyright
© Canadian Mathematical Society 2018 

References

Abdulali, S., Hodge structures on abelian varieties of type III . Ann. of Math. (2) 155(2002), no. 3, 915–928. https://doi.org/10.2307/3062136.Google Scholar
Deligne, P., Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques . In: Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore, 1977), part 2, Proc. Sympos. Pure Math., 33, American Mathematical Society, Providence, RI, 1979, pp. 247–289.Google Scholar
Fulton, W. and Harris, J., Representation theory A first course. Graduate Texts in Mathematics, 129, Readings in Mathematics, Springer-Verlag, New York, 1991. https://doi.org/10.1007/978-1-4612-0979-9.Google Scholar
Friedman, R. and Laza, R., Semialgebraic horizontal subvarieties of Calabi-Yau type . Duke Math. J. 162(2013), no. 12, 2077–2148. https://doi.org/10.1215/00127094-2348107.Google Scholar
Friedman, R. and Laza, R., On some Hermitian variations of Hodge structure of Calabi-Yau type with real multiplication . Michigan Math. J. 63(2014), 83–99. https://doi.org/10.1307/mmj/1395234360.Google Scholar
Green, M., Griffiths, P., and Kerr, M., Mumford-Tate groups and domains. Their geometry and arithmetic. Annals of Mathematics Studies, 183, Princeton University Press, Princeton, NJ, 2012.Google Scholar
Gross, B. H., A remark on tube domains . Math. Res. Lett. 1(1994), 1–9. https://doi.org/10.4310/RL.1994.v1.n1.a1.Google Scholar
Goodman, R. and Wallach, N. R., Symmetry, representations, and invariants. Graduate Texts in Mathematics, 255, Springer, Dordrecht, 2009. https://doi.org/10.1007/978-0-387-79852-3.Google Scholar
Kerr, M., Shimura varieties: a Hodge-theoretic perspective . In: Hodge theory, Math. Notes, 49, Princeton University Press, Princeton, NJ, 2014, pp. 531–575. https://doi.org/10.1007/BF01142652.Google Scholar
Milne, J. S., Shimura varieties and motives . In: Motives (Seattle, WA, 1991), Proc. Sympos. Pure Math., 55, American Mathematical Society, Providence, RI, 1994, pp. 447–523.Google Scholar
Milne, J. S., Shimura varieties and moduli . In: Handbook of Moduli. II, Advanced Lectures in Mathematics, 25, Int. Press, Somerville, MA, 2013, pp. 467–548.Google Scholar
Milne, J. S., Algebraic groups (algebraic group schemes over fields) Version 2.0, 2015. http://www.jmilne.org/math/CourseNotes/iAG200.pdf.Google Scholar
Moonen, B., Notes on Mumford-Tate groups. 1999. https://www.math.ru.nl/∼bmoonen/Lecturenotes/CEBnotesMT.pdf.Google Scholar
Rohde, J. C., Cyclic coverings, Calabi-Yau manifolds and complex multiplication. Lecture Notes in Mathematics, 1975, Springer-Verlag, Berlin, 2009. https://doi.org/10.1007/978-3-642-00639-5.Google Scholar
Satake, I., Holomorphic imbeddings of symmetric domains into a Siegel space . Amer. J. Math. 87(1965), 425–461. https://doi.org/10.2307/2373012.Google Scholar
Sheng, M. and Zuo, K., Polarized variation of Hodge structures of Calabi-Yau type and characteristic subvarieties over bounded symmetric domains . Math. Ann. 348(2010), no. 1, 211–236. https://doi.org/10.1007/s00208-009-0378-9.Google Scholar
van Geemen, B. and Verra, A., Quaternionic Pryms and Hodge classes . Topology 42(2003), 35–53. https://doi.org/10.1016/S0040-9383(02)00004-6.Google Scholar
Zhang, Z., A realization for a ℚ-Hermitian variation of Hodge structure of Calabi-Yau type with real multiplication . Math. Res. Lett. 22(2015), no. 3, 967–982. https://doi.org/10.4310/MRL.2015.v22.n3.a17.Google Scholar