Article contents
On Density Conditions for Interpolation in the Ball
Published online by Cambridge University Press: 20 November 2018
Abstract
In this paper we study interpolating sequences for two related spaces of holomorphic functions in the unit ball of 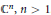 ${{\mathbb{C}}^{n}},\,n\,>\,1$. We first give density conditions for a sequence to be interpolating for the class
${{\mathbb{C}}^{n}},\,n\,>\,1$. We first give density conditions for a sequence to be interpolating for the class 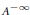 ${{A}^{-\infty }}$ of holomorphic functions with polynomial growth. The sufficient condition is formally identical to the characterizing condition in dimension 1, whereas the necessary one goes along the lines of the results given by Li and Taylor for some spaces of entire functions. In the second part of the paper we show that a density condition, which for
${{A}^{-\infty }}$ of holomorphic functions with polynomial growth. The sufficient condition is formally identical to the characterizing condition in dimension 1, whereas the necessary one goes along the lines of the results given by Li and Taylor for some spaces of entire functions. In the second part of the paper we show that a density condition, which for 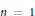 $n\,=\,1$ coincides with the characterizing condition given by Seip, is sufficient for interpolation in the (weighted) Bergman space.
$n\,=\,1$ coincides with the characterizing condition given by Seip, is sufficient for interpolation in the (weighted) Bergman space.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2003
References
- 3
- Cited by


