Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-20T01:12:58.650Z Has data issue: false hasContentIssue false
  • English
  • Français

The Group Aut (μ) is Roelcke Precompact

Published online by Cambridge University Press:  20 November 2018

Eli Glasner
Eli Glasner*
Affiliation:
Department of Mathematics, Tel Aviv University, Ramat Aviv, Israele-mail: glasner@math.tau.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Following a similar result of Uspenskij on the unitary group of a separable Hilbert space, we show that, with respect to the lower (or Roelcke) uniform structure, the Polish group 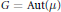$G\,=\,\text{Aut(}\mu \text{)}$ of automorphisms of an atomless standard Borel probability space $(X,\,\mu )$ is precompact. We identify the corresponding compactification as the space of Markov operators on 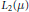${{L}_{2}}(\mu )$ and deduce that the algebra of right and left uniformly continuous functions, the algebra of weakly almost periodic functions, and the algebra of Hilbert functions on 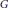$G$, i.e., functions on 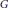$G$ arising from unitary representations, all coincide. Again following Uspenskij, we also conclude that 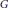$G$ is totally minimal.

Keywords

54H1122A0537B0554H20Roelcke precompactunitary groupmeasure preserving transformationsMarkov operatorsweakly almost periodic functions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 2 , 01 June 2012 , pp. 297 - 302
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Dikranjan, D., Prodanov, I. and Stoyanov, L., Topological groups: Characters, Dualities and Minimal Group Topologies. Monographs and Textbooks in Pure and Applied Mathematics 130. Marcel Dekker, New York, 1990.Google Scholar
[2] Fathi, A., Le groupe de transformations de [0, 1] qui préservent la measure de Lebesgue est un groupe simple. Israel J. Math. 29(1978), no. 2-3, 302–308. http://dx.doi.org/10.1007/BF02762017 Google Scholar
[3] Giordano, T. and Pestov, V., Some extremely amenable groups. C. R. Acad. Sci. Paris 334(2002), no. 4, 273–278.Google Scholar
[4] Giordano, T. and Pestov, V., Some extremely amenable groups related to operator algebras and ergodic theory. J. Inst. Math. Jussieu 6(2007), no. 2, 279–315. http://dx.doi.org/10.1017/S1474748006000090 Google Scholar
[5] Glasner, E., Ergodic Theory via Joinings. Math. Surveys and Monographs 101. American Mathematical Society, Providence, RI, 2003.Google Scholar
[6] Glasner, E. and King, J., A zero-one law for dynamical properties. Contemporary Math. 215(1998), 231–242.Google Scholar
[7] Glasner, E., Lemanczyk, M., and Weiss, B., A topological lens for a measure-preserving system. arXiv:0901.1247.Google Scholar
[8] Glasner, E. and Megrelishvili, M., New algebras of functions on topological groups arising from G-spaces. Fund. Math. 201(2008), no. 1, 1–51. http://dx.doi.org/10.4064/fm201-1-1 Google Scholar
[9] Megrelishvili, M., Reflexively representable but not Hilbert representable compact flows and semitopological semigroups. Colloq. Math. 110(2008), no. 2, 383–407. http://dx.doi.org/10.4064/cm110-2-5 Google Scholar
[10] Roelcke, W. and Dierolf, S., Uniform Structures on Topological Groups and Their Quotients. McGraw-Hill, New York, 1981.Google Scholar
[11] Stoyanov, L., Total minimality of the unitary groups. Math. Z. 187(1984), no. 2, 273–283. http://dx.doi.org/10.1007/BF01161710 Google Scholar
[12] Uspenskij, V. V., The Roelcke compactification of unitary groups. In: Abelian Groups,Module Theory, and Topology. Lecture Notes in Pure and Appl. Math, 201. Dekker, New York, 1998, pp 411–419.Google Scholar
[13] Uspenskij, V. V., The Roelcke compactification of groups of homeomorphisms. Topology Appl. 111(2001), no. 1-2, 195–205. http://dx.doi.org/10.1016/S0166-8641(99)00185-6Google Scholar
[14] Uspenskij, V. V., Compactifications of topological groups. In: Proceedings of the Ninth Prague Topological Symposium. Topol. Atlas, North Bay, ON, 2002, pp. 331–346.Google Scholar
[15] Uspenskij, V. V., On subgroups of minimal topological groups. Topology Appl. 155(2008), no. 14, 1580–1606. http://dx.doi.org/10.1016/j.topol.2008.03.001 Google Scholar