Article contents
Endomorphisms That Are the Sum of a Unit and a Root of a Fixed Polynomial
Published online by Cambridge University Press: 20 November 2018
Abstract
If 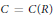 $C=C\left( R \right)$ denotes the center of a ring
$C=C\left( R \right)$ denotes the center of a ring  $R$ and
$R$ and 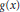 $g\left( x \right)$ is a polynomial in
$g\left( x \right)$ is a polynomial in 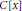 $C\left[ x \right]$, Camillo and Simón called a ring
$C\left[ x \right]$, Camillo and Simón called a ring 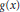 $g\left( x \right)$-clean if every element is the sum of a unit and a root of
$g\left( x \right)$-clean if every element is the sum of a unit and a root of 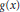 $g\left( x \right)$. If
$g\left( x \right)$. If 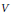 $V$ is a vector space of countable dimension over a division ring
$V$ is a vector space of countable dimension over a division ring 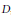 $D$, they showed that
$D$, they showed that 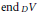 $\text{en}{{\text{d}}_{\,D}}V$ is
$\text{en}{{\text{d}}_{\,D}}V$ is 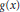 $g\left( x \right)$-clean provided that
$g\left( x \right)$-clean provided that 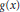 $g\left( x \right)$ has two roots in
$g\left( x \right)$ has two roots in 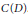 $C\left( D \right)$. If
$C\left( D \right)$. If 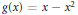 $g\left( x \right)=x-{{x}^{2}}$ this shows that
$g\left( x \right)=x-{{x}^{2}}$ this shows that 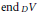 $\text{en}{{\text{d}}_{\,D}}V$ is clean, a result of Nicholson and Varadarajan. In this paper we remove the countable condition, and in fact prove that
$\text{en}{{\text{d}}_{\,D}}V$ is clean, a result of Nicholson and Varadarajan. In this paper we remove the countable condition, and in fact prove that 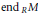 $\text{en}{{\text{d}}_{\,R}}M$ is
$\text{en}{{\text{d}}_{\,R}}M$ is 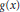 $g\left( x \right)$-clean for any semisimple module
$g\left( x \right)$-clean for any semisimple module 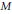 $M$ over an arbitrary ring
$M$ over an arbitrary ring 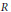 $R$ provided that
$R$ provided that 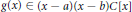 $g\left( x \right)\in \left( x-a \right)\left( x-b \right)C\left[ x \right] $ where
$g\left( x \right)\in \left( x-a \right)\left( x-b \right)C\left[ x \right] $ where 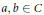 $a,b\in C$ and both
$a,b\in C$ and both 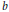 $b$ and
$b$ and 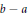 $b-a$ are units in
$b-a$ are units in  $R$.
$R$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2006
References
- 4
- Cited by


